北师大版五年级上册5.8《找最小公倍数》导学案
文档属性
| 名称 | 北师大版五年级上册5.8《找最小公倍数》导学案 |
|
|
| 格式 | doc | ||
| 文件大小 | 56.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 20:34:28 | ||
图片预览

文档简介
8
找最小公倍数
导学案设计
课题
找最小公倍数
课型
新授课
设计说明
“找最小公倍数”是一节概念课,学起来比较枯燥。本课是在学生学习了最大公因数的基础上进行教学的,最大公因数和最小公倍数虽然属于不同的概念,但它们的学习方法相似。通过情境引出公倍数和最小公倍数,既激发了学生的学习兴趣,又使学生在解决去少年宫的问题中初步理解公倍数和最小公倍数的意义。通过练习,在找公倍数的过程中,呈现出找法的多样化,引导学生分析出各种方法的优劣,促进学生思维的个性化发展,然后变换情境中的问题作为进一步学习的材料,引导学生通过多个实例发现其中的规律,加深对公倍数和最小公倍数意义的理解。
课前准备
教师准备 PPT课件学生准备 日历表
教学过程
教学环节
教师指导
学生活动
效果检测
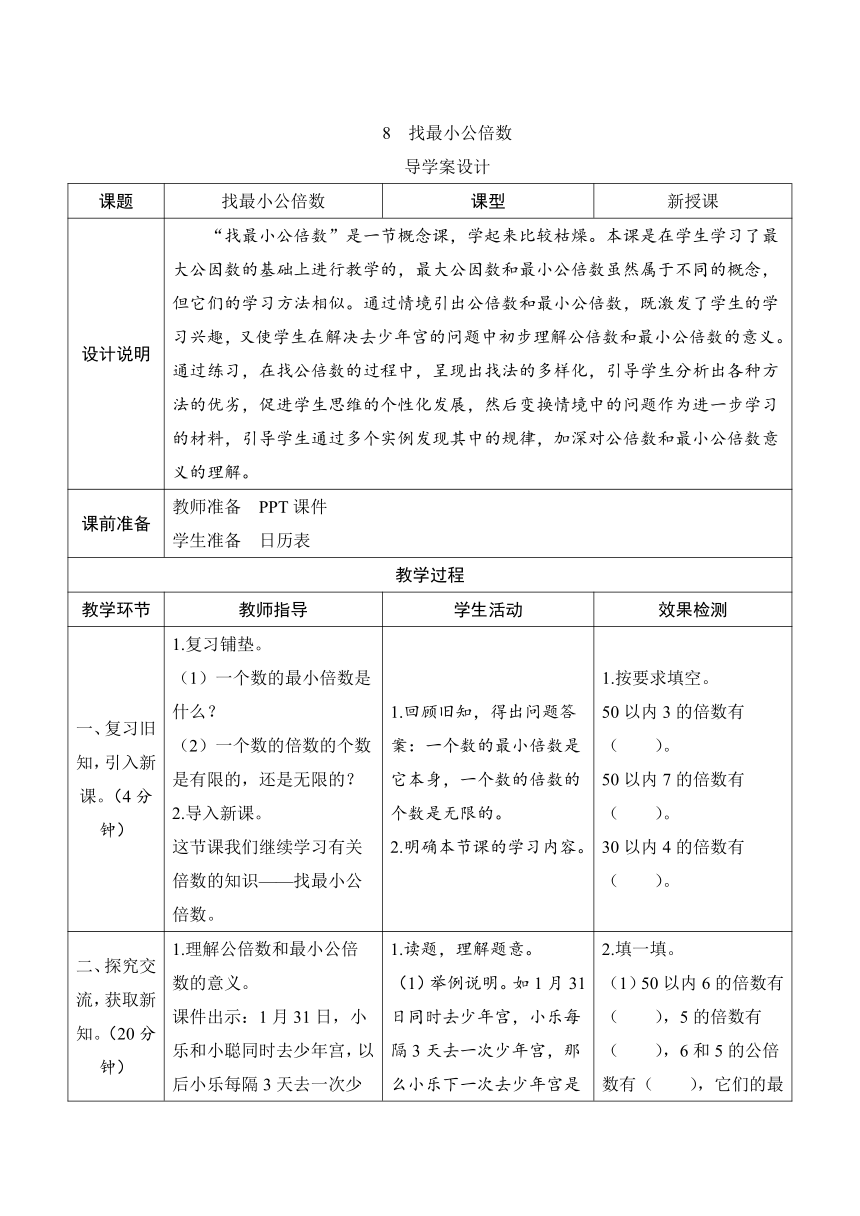
一、复习旧知,引入新课。(4分钟)
1.复习铺垫。(1)一个数的最小倍数是什么?(2)一个数的倍数的个数是有限的,还是无限的?2.导入新课。这节课我们继续学习有关倍数的知识——找最小公倍数。
1.回顾旧知,得出问题答案:一个数的最小倍数是它本身,一个数的倍数的个数是无限的。2.明确本节课的学习内容。
1.按要求填空。50以内3的倍数有( )。50以内7的倍数有( )。30以内4的倍数有( )。
二、探究交流,获取新知。(20分钟)
1.理解公倍数和最小公倍数的意义。课件出示:1月31日,小乐和小聪同时去少年宫,以后小乐每隔3天去一次少年宫,小聪每隔5天去一次少年宫。他们以后同时去少年宫是什么时候?(1)引导学生说一说对“每隔3天去一次和每隔5天去一次”的理解。(2)引导学生探究解题方法。(3)仔细观察这些日期的特点,理解公倍数和最小公倍数的意义。2.深入理解公倍数与最小公倍数的意义。课件出示教材81页例题,根据题意填写课堂活动卡。3.质疑:找公倍数为什么要指定范围(如50以内)?如果不指定范围,是否有最大公倍数?
1.读题,理解题意。(1)举例说明。如1月31日同时去少年宫,小乐每隔3天去一次少年宫,那么小乐下一次去少年宫是2月4日,再下一次去少年宫是2月8日……小聪每隔5天去一次少年宫,那么小聪下一次去少年宫是2月6日,再下一次去少年宫是2月12日……(2)①在2月份的日历表中用不同的符号圈出两人去少年宫的日期。②将这些日期写下来,看看这些日期有什么特点。③把同时标有两种符号的日期写下来。(3)小乐去少年宫的日期都是4的倍数,小聪去少年宫的日期都是6的倍数。同时标有两种符号的日期就是4和6相同的倍数。明确:公倍数就是几个数相同的倍数,其中最小的一个是它们的最小公倍数。2.填写课堂活动卡,小组讨论交流,得出结论:用列举法能找出一组数的最小公倍数。3.思考老师提出的问题,明确:一个数的倍数的个数是无限的,如果不指定范围,就没有最大公倍数。
2.填一填。(1)50以内6的倍数有( ),5的倍数有( ),6和5的公倍数有( ),它们的最小公倍数是( )。(2)两个数相同的倍数是它们的( ),其中( )的一个是它们的最小公倍数。3.找出下面各组数的最小公倍数。10和18的最小公倍数是( )。34和17的最小公倍数是( )。30和50的最小公倍数是( )。24和36的最小公倍数是( )。39和13的最小公倍数是( )。4.判断。(1)两个数的积一定是这两个数的公倍数。( )(2)如果a÷5=b(a≠0,b≠0),那么5和b都是a的倍数。( )(3)a(a≠0)和1没有公倍数。( )
三、巩固练习,深化新知。(12分钟)
1.完成教材82页“练一练”1题。(引导学生发现3和5的倍数的特点)2.完成教材82页“练一练”2题。(让学生掌握找公倍数的另一种方法)3.完成教材82页“练一练”3题。(加深对公倍数和最小公倍数的理解)
1.先独立完成,然后小组内交流。2.先独立完成,然后集体订正。3.先独立填写,然后汇报。
5.一筐鸡蛋,4个4个地数或5个5个地数都能正好数完,这筐鸡蛋最少有多少个?
四、课堂总结,拓展延伸。(4分钟)
1.总结本课学习内容。2.布置课后学习内容。
谈自己本节课的收获。
教师批注
板书设计
找最小公倍数公倍数和最小公倍数的意义几个数相同的倍数,叫作这几个数的公倍数,其中最小的一个,叫作它们的最小公倍数。公倍数的特点在指定范围内,公倍数的个数是有限的;不指定范围,公倍数的个数是无限的。求公倍数的方法列举法。
找最小公倍数
导学案设计
课题
找最小公倍数
课型
新授课
设计说明
“找最小公倍数”是一节概念课,学起来比较枯燥。本课是在学生学习了最大公因数的基础上进行教学的,最大公因数和最小公倍数虽然属于不同的概念,但它们的学习方法相似。通过情境引出公倍数和最小公倍数,既激发了学生的学习兴趣,又使学生在解决去少年宫的问题中初步理解公倍数和最小公倍数的意义。通过练习,在找公倍数的过程中,呈现出找法的多样化,引导学生分析出各种方法的优劣,促进学生思维的个性化发展,然后变换情境中的问题作为进一步学习的材料,引导学生通过多个实例发现其中的规律,加深对公倍数和最小公倍数意义的理解。
课前准备
教师准备 PPT课件学生准备 日历表
教学过程
教学环节
教师指导
学生活动
效果检测
一、复习旧知,引入新课。(4分钟)
1.复习铺垫。(1)一个数的最小倍数是什么?(2)一个数的倍数的个数是有限的,还是无限的?2.导入新课。这节课我们继续学习有关倍数的知识——找最小公倍数。
1.回顾旧知,得出问题答案:一个数的最小倍数是它本身,一个数的倍数的个数是无限的。2.明确本节课的学习内容。
1.按要求填空。50以内3的倍数有( )。50以内7的倍数有( )。30以内4的倍数有( )。
二、探究交流,获取新知。(20分钟)
1.理解公倍数和最小公倍数的意义。课件出示:1月31日,小乐和小聪同时去少年宫,以后小乐每隔3天去一次少年宫,小聪每隔5天去一次少年宫。他们以后同时去少年宫是什么时候?(1)引导学生说一说对“每隔3天去一次和每隔5天去一次”的理解。(2)引导学生探究解题方法。(3)仔细观察这些日期的特点,理解公倍数和最小公倍数的意义。2.深入理解公倍数与最小公倍数的意义。课件出示教材81页例题,根据题意填写课堂活动卡。3.质疑:找公倍数为什么要指定范围(如50以内)?如果不指定范围,是否有最大公倍数?
1.读题,理解题意。(1)举例说明。如1月31日同时去少年宫,小乐每隔3天去一次少年宫,那么小乐下一次去少年宫是2月4日,再下一次去少年宫是2月8日……小聪每隔5天去一次少年宫,那么小聪下一次去少年宫是2月6日,再下一次去少年宫是2月12日……(2)①在2月份的日历表中用不同的符号圈出两人去少年宫的日期。②将这些日期写下来,看看这些日期有什么特点。③把同时标有两种符号的日期写下来。(3)小乐去少年宫的日期都是4的倍数,小聪去少年宫的日期都是6的倍数。同时标有两种符号的日期就是4和6相同的倍数。明确:公倍数就是几个数相同的倍数,其中最小的一个是它们的最小公倍数。2.填写课堂活动卡,小组讨论交流,得出结论:用列举法能找出一组数的最小公倍数。3.思考老师提出的问题,明确:一个数的倍数的个数是无限的,如果不指定范围,就没有最大公倍数。
2.填一填。(1)50以内6的倍数有( ),5的倍数有( ),6和5的公倍数有( ),它们的最小公倍数是( )。(2)两个数相同的倍数是它们的( ),其中( )的一个是它们的最小公倍数。3.找出下面各组数的最小公倍数。10和18的最小公倍数是( )。34和17的最小公倍数是( )。30和50的最小公倍数是( )。24和36的最小公倍数是( )。39和13的最小公倍数是( )。4.判断。(1)两个数的积一定是这两个数的公倍数。( )(2)如果a÷5=b(a≠0,b≠0),那么5和b都是a的倍数。( )(3)a(a≠0)和1没有公倍数。( )
三、巩固练习,深化新知。(12分钟)
1.完成教材82页“练一练”1题。(引导学生发现3和5的倍数的特点)2.完成教材82页“练一练”2题。(让学生掌握找公倍数的另一种方法)3.完成教材82页“练一练”3题。(加深对公倍数和最小公倍数的理解)
1.先独立完成,然后小组内交流。2.先独立完成,然后集体订正。3.先独立填写,然后汇报。
5.一筐鸡蛋,4个4个地数或5个5个地数都能正好数完,这筐鸡蛋最少有多少个?
四、课堂总结,拓展延伸。(4分钟)
1.总结本课学习内容。2.布置课后学习内容。
谈自己本节课的收获。
教师批注
板书设计
找最小公倍数公倍数和最小公倍数的意义几个数相同的倍数,叫作这几个数的公倍数,其中最小的一个,叫作它们的最小公倍数。公倍数的特点在指定范围内,公倍数的个数是有限的;不指定范围,公倍数的个数是无限的。求公倍数的方法列举法。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
