1.3正方形的性质与判定 能力提升训练(附答案) 2021-2022学年北师大版九年级数学上册(word版含解析)
文档属性
| 名称 | 1.3正方形的性质与判定 能力提升训练(附答案) 2021-2022学年北师大版九年级数学上册(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 00:00:00 | ||
图片预览

文档简介
2021-2022学年北师大版九年级数学上册《1.3正方形的性质与判定》
能力提升训练(附答案)
1.下列性质中不是正方形和菱形共有的是( )
A.相邻两角都互补
B.相邻两边都相等
C.对角线所在直线是对称轴
D.对角线垂直且相等
2.如图,在正方形OABC中,O是坐标原点,点A的坐标为(1,),则点C的坐标是( )
A.(﹣,1)
B.(﹣1,)
C.(,1)
D.(﹣,﹣1)
3.如图,延长正方形ABCD边B至点E,使AE=BD,则∠E为( )
A.22.5°
B.25°
C.30°
D.45°
4.如图,正方形ABCD中,点E是对角线BD上的一点,且BE=AB,连接CE,AE,则∠DAE的度数为( )
A.22.5°
B.25°
C.30°
D.32.5°
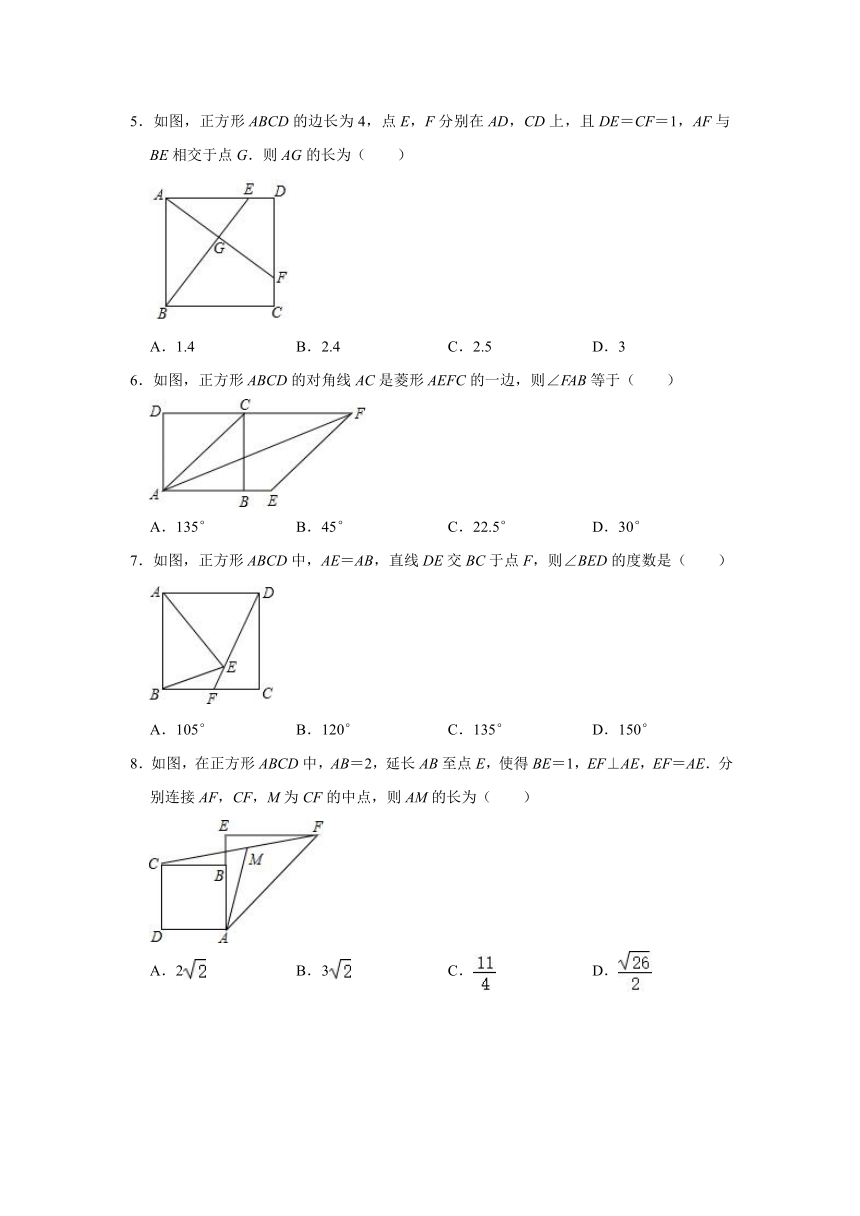
5.如图,正方形ABCD的边长为4,点E,F分别在AD,CD上,且DE=CF=1,AF与BE相交于点G.则AG的长为( )
A.1.4
B.2.4
C.2.5
D.3
6.如图,正方形ABCD的对角线AC是菱形AEFC的一边,则∠FAB等于( )
A.135°
B.45°
C.22.5°
D.30°
7.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BED的度数是( )
A.105°
B.120°
C.135°
D.150°
8.如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )
A.2
B.3
C.
D.
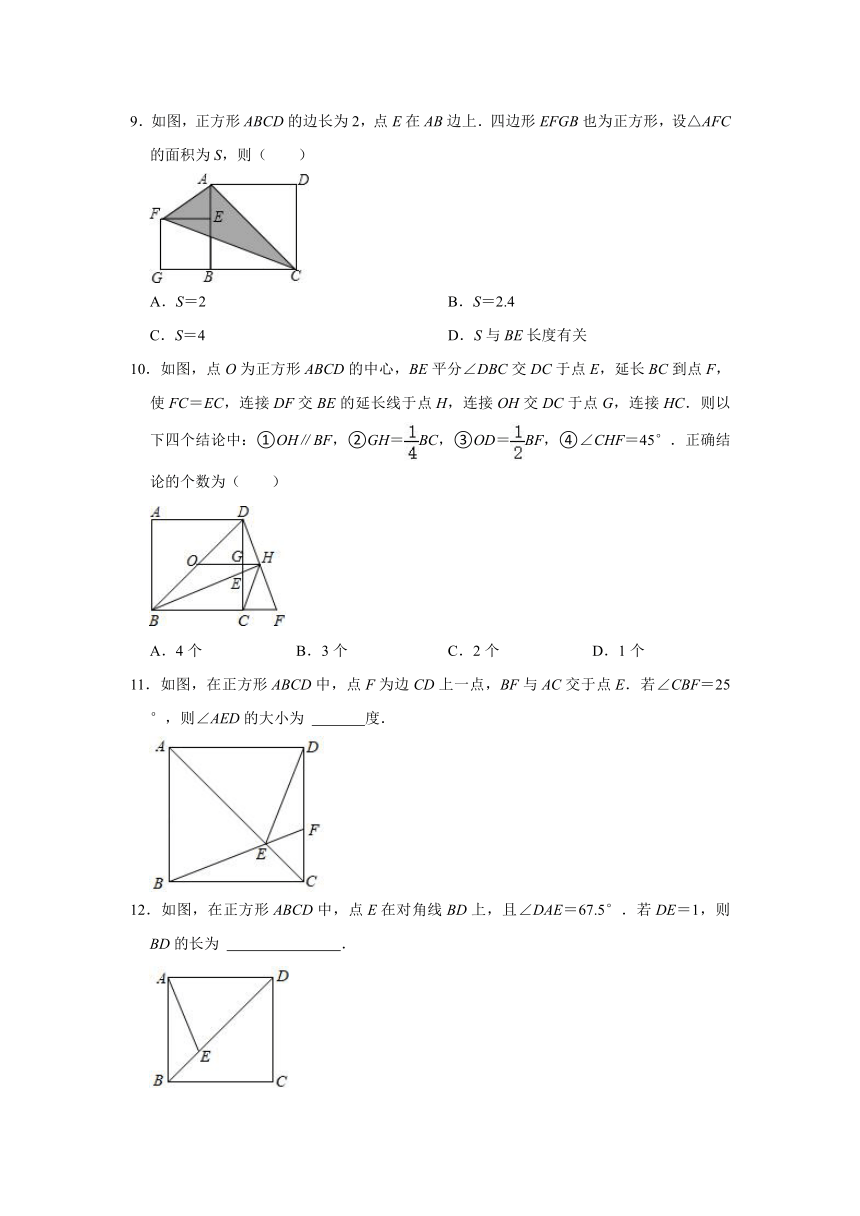
9.如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则( )
A.S=2
B.S=2.4
C.S=4
D.S与BE长度有关
10.如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中:①OH∥BF,②GH=BC,③OD=BF,④∠CHF=45°.正确结论的个数为( )
A.4个
B.3个
C.2个
D.1个
11.如图,在正方形ABCD中,点F为边CD上一点,BF与AC交于点E.若∠CBF=25°,则∠AED的大小为
度.
12.如图,在正方形ABCD中,点E在对角线BD上,且∠DAE=67.5°.若DE=1,则BD的长为
.
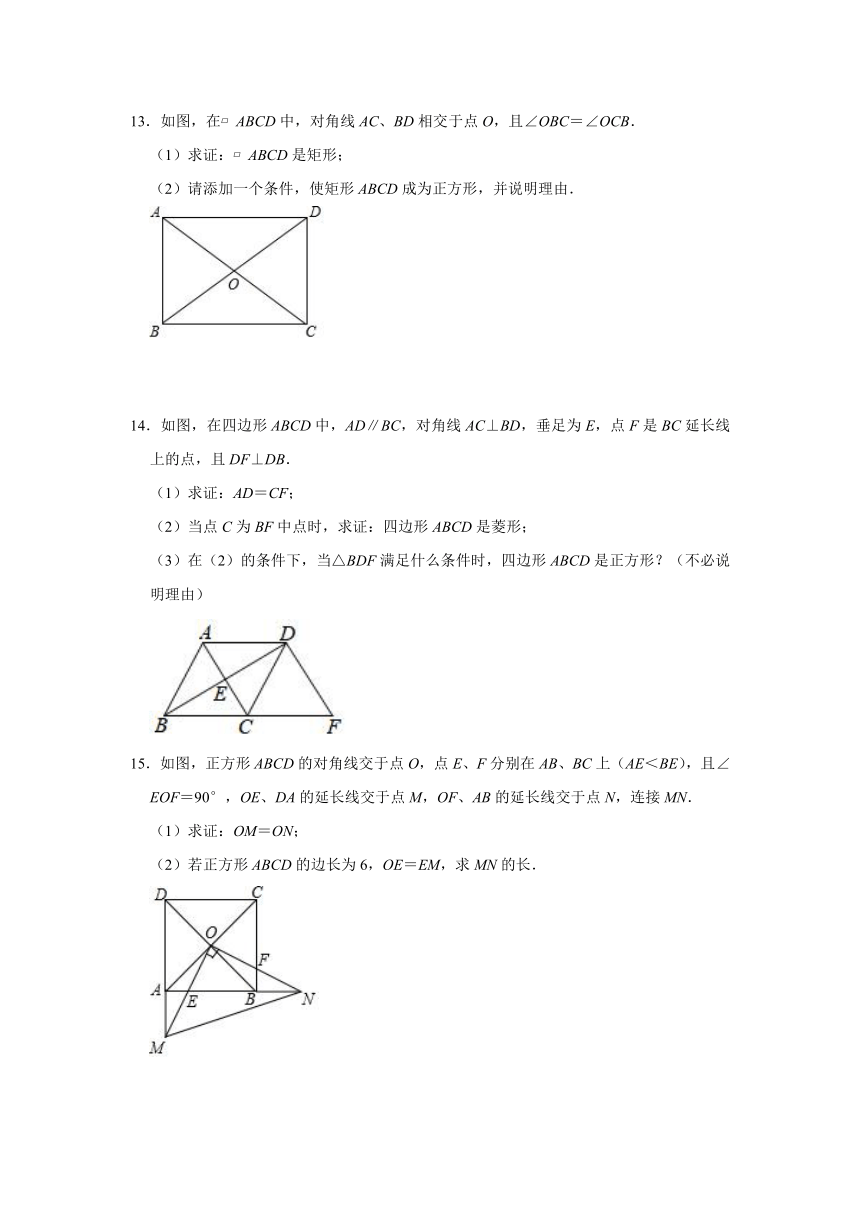
13.如图,在?ABCD中,对角线AC、BD相交于点O,且∠OBC=∠OCB.
(1)求证:?ABCD是矩形;
(2)请添加一个条件,使矩形ABCD成为正方形,并说明理由.
14.如图,在四边形ABCD中,AD∥BC,对角线AC⊥BD,垂足为E,点F是BC延长线上的点,且DF⊥DB.
(1)求证:AD=CF;
(2)当点C为BF中点时,求证:四边形ABCD是菱形;
(3)在(2)的条件下,当△BDF满足什么条件时,四边形ABCD是正方形?(不必说明理由)
15.如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.
(1)求证:OM=ON;
(2)若正方形ABCD的边长为6,OE=EM,求MN的长.
16.如图,已知平行四边形ABCD,对角AC与BD交于点O,以AD、AB边分别为边长作正方形ADEF和正方形ABHG,连接FG.
(1)求证:FG=2AO;
(2)若AB=6,AD=4,∠BAD=60°,请求出△AGF的面积.
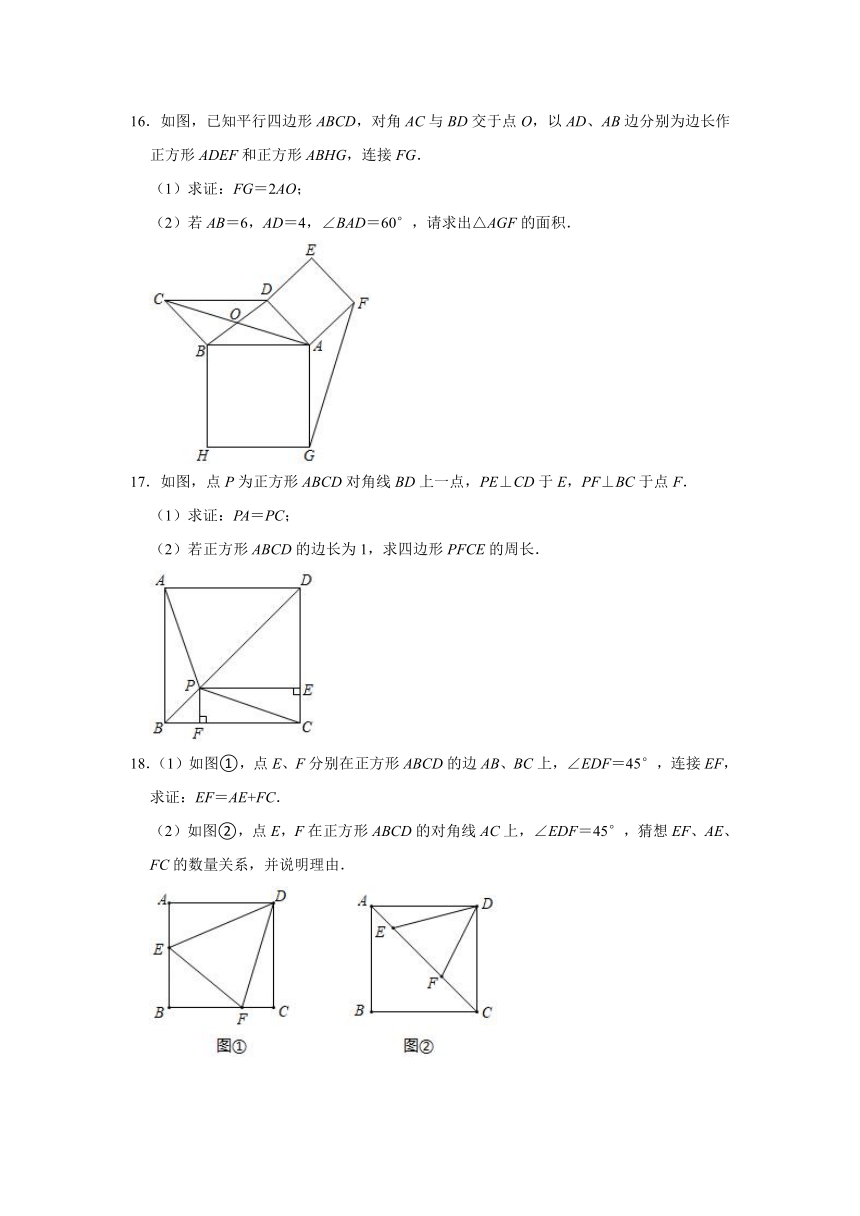
17.如图,点P为正方形ABCD对角线BD上一点,PE⊥CD于E,PF⊥BC于点F.
(1)求证:PA=PC;
(2)若正方形ABCD的边长为1,求四边形PFCE的周长.
18.(1)如图①,点E、F分别在正方形ABCD的边AB、BC上,∠EDF=45°,连接EF,求证:EF=AE+FC.
(2)如图②,点E,F在正方形ABCD的对角线AC上,∠EDF=45°,猜想EF、AE、FC的数量关系,并说明理由.
19.如图,在正方形ABCD中,点E是对角线BD上的一点(DE<BE),连接AE,过点E分别作EF⊥AE交BC于点F,EG⊥BD交BC的延长线于点G.
(1)若AD=2,DE=1,求EG的长度;
(2)求证:FG=AB.
20.如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且AF=AD,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
(1)求证:AE=GE;
(2)求证:CG=DE.
21.如图,正方形ABCD和正方形BEFG有公共顶点B,且顶点A,G,F三点共线,顶点C,F,E三点共线,DM⊥AG于点M,AB=15,BE=9.
(1)求证:△ABG≌△DAM;
(2)连接DG,求DG的长;
(3)直接写出△ABH与△CFH的面积差.
22.已知四边形ABCD是正方形,点E在边DA的延长线上,连接CE交AB于点G,过点B作BM⊥CE,垂足为点M,BM的延长线交AD于点F,交CD的延长线于点H.
(1)如图1,求证:CE=BH;
(2)如图2,若AE=AB,连接CF,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(△AEG除外),使写出的每个三角形都与△AEG全等.
参考答案
1.解:∵正方形和菱形都属于平行四边形,平行四边形邻角互补,
∴选项A不符合题意;
∵正方形和菱形的四边均相等,
∴选项B不符合题意;
∵正方形和菱形都关于对角线所在的直线对称,
∴选项C不符合题意;
∵正方形的对角线垂直且相等,菱形的对角线相互垂直平分,
∴选项D符合题意;
故选:D.
2.解:如图,过点C作CD⊥x轴于点D,
在正方形OABC中,∠AOC=90°,AO=CO,
∵∠AOC=∠CDO=90°,
∴∠COD+∠AOE=∠COD+∠OCD=90°,
∴∠OCD=∠AOE,
在△OCD和△AOE中,
,
∴△OCD≌△AOE(AAS),
∴CD=OE=1,OD=AE=,
∴C(﹣,1).
故选:A.
3.解:连接AC,
∵四边形ABCD是正方形,
∴AC=BD,且∠CAB=45°,
又∵BD=AE,
∴AE=CA,
∴∠E=∠ACE,
∵∠CAB=∠ACE+∠E=2∠E=45°,
∴∠E=22.5°.
故选:A.
4.解:∵四边形ABCD为正方形,
∴∠ABD=45°,∠BAD=90°,
∵BE=AB,
∴∠BAE=∠BEA=×(180°﹣45°)=67.5°,
∴∠DAE=∠BAD﹣∠BAE=90°﹣67.5°=22.5°.
故选:A.
5.解:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD=CD,
∵DE=CF,
∴AE=DF,
在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS),
∴∠EBA=∠FAD,
∴∠GAE+∠AEG=90°,
∴∠AGE=90°,
∵AB=4,DE=1,
∴AE=3,
∴BE==5,
在Rt△ABE中,AB×AE=BE×AG,
∴AG==2.4,
故选:B.
6.解:∵AC是正方形的对角线,
∴∠BAC=×90°=45°,
∵AF是菱形AEFC的对角线,
∴∠FAB=∠BAC=×45°=22.5°.
故选:C.
7.解:设∠BAE=x°,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵AE=AB,
∴AB=AE=AD,
∴∠ABE=∠AEB=(180°﹣∠BAE)=90°﹣x°,
∴∠DAE=90°﹣x°
∴∠AED=∠ADE=(180°﹣∠DAE)=[180°﹣(90°﹣x°)]=45°+x°,
∴∠BED=90°﹣x°+45°+x°=135°.
故选:C.
8.解:连接AC,
∵四边形ABCD是正方形,
∴∠BAC=45°.
∵EF⊥AE,EF=AE,
∴△AEF是等腰直角三角形,
∴∠EAF=45°,
∴∠CAF=90°.
∵AB=BC=2,
∴AC==2.
∵AE=EF=AB+BE=2+1=3,
∴AF==3,
∴CF===.
∵M为CF的中点,
∴AM=CF=.
故选:D.
9.解:连接FB
∵四边形EFGB为正方形
∴∠FBA=∠BAC=45°,
∴FB∥AC
∴△ABC与△AFC是同底等高的三角形
∵2S△ABC=S正ABCD,S正ABCD=2×2=4
∴S=2
故选:A.
10.解:∵EC=CF,∠BCE=∠DCF,BC=DC,
∴△BCE≌△DCF,
∴∠CBE=∠CDF,
∵∠CBE+∠BEC=90°,∠BEC=∠DEH,
∴∠DEH+∠CDF=90°,
∴∠BHD=∠BHF=90°,
∵BH=BH,∠HBD=∠HBF,
∴△BHD≌△BHF,
∴DH=HF,∵OD=OB
∴OH是△DBF的中位线
∴OH∥BF;故①正确;
∴OH=BF,∠DOH=∠CBD=45°,
∵OH是△BFD的中位线,
∴DG=CG=BC,GH=CF,
∵CE=CF,
∴GH=CF=CE
∵CE<CG=BC,
∴GH<BC,故②错误.
∵四边形ABCD是正方形,BE是∠DBC的平分线,
∴BC=CD,∠BCD=∠DCF,∠EBC=22.5°,
∵CE=CF,
∴Rt△BCE≌Rt△DCF(SAS),
∴∠EBC=∠CDF=22.5°,
∴∠BFH=90°﹣∠CDF=90°﹣22.5°=67.5°,
∵OH是△DBF的中位线,CD⊥AF,
∴OH是CD的垂直平分线,
∴DH=CH,
∴∠CDF=∠DCH=22.5°,
∴∠HCF=90°﹣∠DCH=90°﹣22.5°=67.5°,
∴∠CHF=180°﹣∠HCF﹣∠BFH=180°﹣67.5°﹣67.5°=45°,故④正确;
∴∠ODH=∠BDC+∠CDF=67.5°,
∴∠OHD=180°﹣∠ODH﹣∠DOH=67.5°,
∴∠ODH=∠OHD,
∴OD=OH=BF;故③正确.
故选:B.
11.解:∵四边形ABCD是正方形,且AC为正方ABCD的对角线,
∴△ABE与△ADE关于直线AC对称,∠ACB=45°,
∴∠AED=∠AEB,
∵∠AEB为△EBC的外角,
∴∠AEB=∠CBE+∠ACB=25°+45°=70°,
∴∠AED=70°,
故答案为70.
12.解:∵四边形ABCD是正方形,
∴AB=CD,∠BAD=90°,∠ADB=45°,
∵∠DAE=67.5°,
∴∠EAD=180°﹣45°﹣67.5°=67.5°,
∴AD=DE=1,
在Rt△ABD中,AB=AD=1,
∴AC==,
故答案为.
13.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵∠OBC=∠OCB,
∴OB=OC,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:AB=AD(答案不唯一).
理由:∵四边形ABCD是矩形,
又∵AB=AD,
∴四边形ABCD是正方形.
14.(1)证明:∵AC⊥BD,DF⊥DB,
∴AC∥DF,
∵AD∥BC,
∴四边形ACFD是平行四边形,
∴AD=CF;
(2)证明:∵点C为BF中点,
∴BC=CF,
∵AD=CF,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵DF⊥DB,BC=CF,
∴DC=BC=BF,
∴四边形ABCD是菱形;
(3)解:当△BDF满足是等腰三角形时(BD=DF),四边形ABCD是正方形.
证明:∵DF⊥DB,
∴∠BDF=90°,
∵BD=DF,
∴∠DBF=∠DFB=(180°﹣∠BDF)=×(180°﹣90°)=45°,
由(2)知,四边形ABCD是菱形,
∴∠ABD=∠DBF=45°,
∴∠ABC=∠ABD+∠DBF=45°+45°=90°,
∵四边形ABCD是菱形,
∴四边形ABCD是正方形.
15.解:(1)∵四边形ABCD是正方形,
∴OA=OB,∠DAO=45°,∠OBA=45°,
∴∠OAM=∠OBN=135°,
∵∠EOF=90°,∠AOB=90°,
∴∠AOM=∠BON,
∴△OAM≌△OBN(ASA),
∴OM=ON;
(2)如图,过点O作OH⊥AD于点H,
∵正方形的边长为6,
∴OH=HA=3,
∵E为OM的中点,
∴HM=6,
则OM==3,
∴MN=OM=3.
16.(1)证明:∵四边形ADEF和四边形ABHG都是正方形,
∴AD=AF,AB=AG,∠BAG=∠DAF=90°,
∴∠GAF+∠BAD=180°,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAD+∠ADC=180°,
∴∠GAF=∠ADC,
在△AFG和△DAC中,
,
∴△AFG≌△DAC(SAS),
∴GF=AC,
∵平行四边形ABCD中,AC=2AO,
∴GF=2AO;
(2)解:过点D作DM⊥AB于点M,
∵AD=4,∠BAD=60°,∠AMD=90°,
∴DM=4×sin60°=4×=2,
∴S平行四边形ABCD=AB?DM=6×2=12,
∴S△DAC=,
∵△AFG≌△DAC,
∴S△DAC=S△AGF=6.
即△AGF的面积为6.
17.证明:(1)∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD=45°,∠C=90°,
在△ABP与△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC;
(2)∵PE⊥CD,PF⊥BC,
∴∠PFC=90°,∠PEC=90°.
又∵∠BCD=90°,
∴四边形PFCE是矩形,
∴EC=PF,PE=CF,
∵∠CBD=45°,∠PFB=90°,
∴BF=PF,
又∵BC=1,
∴矩形PFCE的周长为2(PF+FC)=2(BF+FC)=2BC=2.
18.证明:(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠C=∠ADC=∠DAB=90°,
如图①:延长BA,使AM=CF,连接MD,
在△AMD和△CFD中,
,
∴△AMD≌△CFD(SAS),
∴∠MDA=∠CDF,MD=DF,
∵∠EDF=45°,
∴∠ADE+∠FDC=45°,
∴∠ADM+∠ADE=45°=∠MDE,
∴∠MDE=∠EDF,
在△EDF和△EDM中,
,
∴△EDF≌△EDM(SAS),
∴EF=EM,
∵EM=AM+AE=AE+CF,
∴EF=AE+CF;
(2)EF2=AE2+CF2,
理由如下:
如图②,将△CDF绕点D顺时针旋转90°,可得△ADN,
由旋转的性质可得DN=DF,AN=CF,∠DAN=∠DCF=45°,∠CDF=∠ADN,
∴∠CAN=∠CAD+∠DAN=90°,
∴EN2=AE2+AN2,
∵∠EDF=45°,
∴∠CDF+∠ADE=45°,
∴∠ADE+∠ADN=45°=∠NDE=∠EDF,
在△EDF和△EDN中,
,
∴△EDF≌△EDN(SAS),
∴EF=EN,
∴EF2=AE2+CF2.
19.解:(1)∵四边形ABCD是正方形,
∴AD=AB=2,BD=AD=2,∠ABD=∠CBD=45°,
∴BE=BD﹣DE=2﹣1,
∵EG⊥BD,∠DBG=45°,
∴∠DBG=∠EGB=45°,
∴EB=EG=2﹣1;
(2)∵AE⊥EF,
∴∠AEF=∠BEG=90°,
∴∠AEB=∠GEF,
又∵BE=EG,∠ABD=∠FGE=45°,
∴△ABE≌△FGE(AAS),
∴FG=AB.
20.证明:(1)∵AF=AD,AE⊥DF,
∴∠DAE=∠EAF=∠DAF,
∵AF平分∠EAF,
∴∠BAG=∠FAG=∠BAF,
∵∠GAE=∠EAF﹣∠FAG=(∠DAF﹣∠BAF),
∴∠GAE=45°,
∴∠GAE=∠AGE=45°,
∴AE=GE;
(2)如图,过点C作CH⊥DF于H,
∴∠AED=∠CHD=90°,
∴∠ADE+∠EAD=90°=∠ADE+∠CDH,
∴∠EAD=∠CDH,
在△ADE和△DCH中,
,
∴△ADE≌△DCH(AAS),
∴CH=DE,DH=AE=GE,
∴DE=GH=CH,
∴GC=CH=DE.
21.(1)证明:∵四边形ABCD和四边形BEFG是正方形,
∴∠BAD=∠FGB=90°,AB=AD,
∵DM⊥AG,
∴∠DMA=∠AGB=90°,
∵∠DAM+∠GAB=90°,∠DAM+∠ADM=90°,
∴∠ADM=∠GAB,
∴△ABG≌△DAM(AAS);
(2)解:在Rt△ABG中,AG==12,
∵△ABG≌△DAM,
∴DM=AG=12,AM=BG=9,
∴MG=AG﹣AM=3,
在Rt△DMG中,DG==3;
(3)解:∵四边形ABCD和四边形BEFG是正方形,
∴∠ABC=∠GBE=90°,AB=BC,
∴∠ABG=∠CBE,
∴△ABG≌△CBE(SAS),
∴S△ABG=S△CBE,
∵S△ABH﹣S△CHF=S△ABH+S四边形BHFE﹣(S△CHF+S四边形HFEB)=S△ABG+S正方形GBFE﹣S△CBE=S正方形BGFE=92=81,
∴△ABH与△CFH的面积差为81.
22.证明:(1)∵四边形ABCD是正方形,
∴BC=CD=AD=AB,∠BCD=∠ADC=90°,
∵BM⊥CE,
∴∠HMC=∠ADC=90°,
∴∠H+∠HCM=90°=∠E+∠ECD,
∴∠H=∠E,
在△EDC和△HCB中,
,
∴△EDC≌△HCB(AAS),
∴CE=BH;
(2)△BCG,△DCF,△DHF,△ABF,
理由如下:∵AE=AB,
∴AE=BC=AD=CD,
∵△EDC≌△HCB,
∴ED=HC,
∵AD=CD,
∴AE=HD=CD=AB,
在△AEG和△BCG中,
,
∴△AEG≌△BCG(AAS),
∴AG=BG=AB,
同理可证△AFB≌△DFH,
∴AF=DF=AD,
∴AG=AF=DF,
在△AEG和△ABF中,
,
∴△AEG≌△ABF(SAS),
同理可证△AEG≌△DHF,△AEG≌△DCF.
能力提升训练(附答案)
1.下列性质中不是正方形和菱形共有的是( )
A.相邻两角都互补
B.相邻两边都相等
C.对角线所在直线是对称轴
D.对角线垂直且相等
2.如图,在正方形OABC中,O是坐标原点,点A的坐标为(1,),则点C的坐标是( )
A.(﹣,1)
B.(﹣1,)
C.(,1)
D.(﹣,﹣1)
3.如图,延长正方形ABCD边B至点E,使AE=BD,则∠E为( )
A.22.5°
B.25°
C.30°
D.45°
4.如图,正方形ABCD中,点E是对角线BD上的一点,且BE=AB,连接CE,AE,则∠DAE的度数为( )
A.22.5°
B.25°
C.30°
D.32.5°
5.如图,正方形ABCD的边长为4,点E,F分别在AD,CD上,且DE=CF=1,AF与BE相交于点G.则AG的长为( )
A.1.4
B.2.4
C.2.5
D.3
6.如图,正方形ABCD的对角线AC是菱形AEFC的一边,则∠FAB等于( )
A.135°
B.45°
C.22.5°
D.30°
7.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BED的度数是( )
A.105°
B.120°
C.135°
D.150°
8.如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )
A.2
B.3
C.
D.
9.如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则( )
A.S=2
B.S=2.4
C.S=4
D.S与BE长度有关
10.如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中:①OH∥BF,②GH=BC,③OD=BF,④∠CHF=45°.正确结论的个数为( )
A.4个
B.3个
C.2个
D.1个
11.如图,在正方形ABCD中,点F为边CD上一点,BF与AC交于点E.若∠CBF=25°,则∠AED的大小为
度.
12.如图,在正方形ABCD中,点E在对角线BD上,且∠DAE=67.5°.若DE=1,则BD的长为
.
13.如图,在?ABCD中,对角线AC、BD相交于点O,且∠OBC=∠OCB.
(1)求证:?ABCD是矩形;
(2)请添加一个条件,使矩形ABCD成为正方形,并说明理由.
14.如图,在四边形ABCD中,AD∥BC,对角线AC⊥BD,垂足为E,点F是BC延长线上的点,且DF⊥DB.
(1)求证:AD=CF;
(2)当点C为BF中点时,求证:四边形ABCD是菱形;
(3)在(2)的条件下,当△BDF满足什么条件时,四边形ABCD是正方形?(不必说明理由)
15.如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.
(1)求证:OM=ON;
(2)若正方形ABCD的边长为6,OE=EM,求MN的长.
16.如图,已知平行四边形ABCD,对角AC与BD交于点O,以AD、AB边分别为边长作正方形ADEF和正方形ABHG,连接FG.
(1)求证:FG=2AO;
(2)若AB=6,AD=4,∠BAD=60°,请求出△AGF的面积.
17.如图,点P为正方形ABCD对角线BD上一点,PE⊥CD于E,PF⊥BC于点F.
(1)求证:PA=PC;
(2)若正方形ABCD的边长为1,求四边形PFCE的周长.
18.(1)如图①,点E、F分别在正方形ABCD的边AB、BC上,∠EDF=45°,连接EF,求证:EF=AE+FC.
(2)如图②,点E,F在正方形ABCD的对角线AC上,∠EDF=45°,猜想EF、AE、FC的数量关系,并说明理由.
19.如图,在正方形ABCD中,点E是对角线BD上的一点(DE<BE),连接AE,过点E分别作EF⊥AE交BC于点F,EG⊥BD交BC的延长线于点G.
(1)若AD=2,DE=1,求EG的长度;
(2)求证:FG=AB.
20.如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且AF=AD,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
(1)求证:AE=GE;
(2)求证:CG=DE.
21.如图,正方形ABCD和正方形BEFG有公共顶点B,且顶点A,G,F三点共线,顶点C,F,E三点共线,DM⊥AG于点M,AB=15,BE=9.
(1)求证:△ABG≌△DAM;
(2)连接DG,求DG的长;
(3)直接写出△ABH与△CFH的面积差.
22.已知四边形ABCD是正方形,点E在边DA的延长线上,连接CE交AB于点G,过点B作BM⊥CE,垂足为点M,BM的延长线交AD于点F,交CD的延长线于点H.
(1)如图1,求证:CE=BH;
(2)如图2,若AE=AB,连接CF,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(△AEG除外),使写出的每个三角形都与△AEG全等.
参考答案
1.解:∵正方形和菱形都属于平行四边形,平行四边形邻角互补,
∴选项A不符合题意;
∵正方形和菱形的四边均相等,
∴选项B不符合题意;
∵正方形和菱形都关于对角线所在的直线对称,
∴选项C不符合题意;
∵正方形的对角线垂直且相等,菱形的对角线相互垂直平分,
∴选项D符合题意;
故选:D.
2.解:如图,过点C作CD⊥x轴于点D,
在正方形OABC中,∠AOC=90°,AO=CO,
∵∠AOC=∠CDO=90°,
∴∠COD+∠AOE=∠COD+∠OCD=90°,
∴∠OCD=∠AOE,
在△OCD和△AOE中,
,
∴△OCD≌△AOE(AAS),
∴CD=OE=1,OD=AE=,
∴C(﹣,1).
故选:A.
3.解:连接AC,
∵四边形ABCD是正方形,
∴AC=BD,且∠CAB=45°,
又∵BD=AE,
∴AE=CA,
∴∠E=∠ACE,
∵∠CAB=∠ACE+∠E=2∠E=45°,
∴∠E=22.5°.
故选:A.
4.解:∵四边形ABCD为正方形,
∴∠ABD=45°,∠BAD=90°,
∵BE=AB,
∴∠BAE=∠BEA=×(180°﹣45°)=67.5°,
∴∠DAE=∠BAD﹣∠BAE=90°﹣67.5°=22.5°.
故选:A.
5.解:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD=CD,
∵DE=CF,
∴AE=DF,
在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS),
∴∠EBA=∠FAD,
∴∠GAE+∠AEG=90°,
∴∠AGE=90°,
∵AB=4,DE=1,
∴AE=3,
∴BE==5,
在Rt△ABE中,AB×AE=BE×AG,
∴AG==2.4,
故选:B.
6.解:∵AC是正方形的对角线,
∴∠BAC=×90°=45°,
∵AF是菱形AEFC的对角线,
∴∠FAB=∠BAC=×45°=22.5°.
故选:C.
7.解:设∠BAE=x°,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵AE=AB,
∴AB=AE=AD,
∴∠ABE=∠AEB=(180°﹣∠BAE)=90°﹣x°,
∴∠DAE=90°﹣x°
∴∠AED=∠ADE=(180°﹣∠DAE)=[180°﹣(90°﹣x°)]=45°+x°,
∴∠BED=90°﹣x°+45°+x°=135°.
故选:C.
8.解:连接AC,
∵四边形ABCD是正方形,
∴∠BAC=45°.
∵EF⊥AE,EF=AE,
∴△AEF是等腰直角三角形,
∴∠EAF=45°,
∴∠CAF=90°.
∵AB=BC=2,
∴AC==2.
∵AE=EF=AB+BE=2+1=3,
∴AF==3,
∴CF===.
∵M为CF的中点,
∴AM=CF=.
故选:D.
9.解:连接FB
∵四边形EFGB为正方形
∴∠FBA=∠BAC=45°,
∴FB∥AC
∴△ABC与△AFC是同底等高的三角形
∵2S△ABC=S正ABCD,S正ABCD=2×2=4
∴S=2
故选:A.
10.解:∵EC=CF,∠BCE=∠DCF,BC=DC,
∴△BCE≌△DCF,
∴∠CBE=∠CDF,
∵∠CBE+∠BEC=90°,∠BEC=∠DEH,
∴∠DEH+∠CDF=90°,
∴∠BHD=∠BHF=90°,
∵BH=BH,∠HBD=∠HBF,
∴△BHD≌△BHF,
∴DH=HF,∵OD=OB
∴OH是△DBF的中位线
∴OH∥BF;故①正确;
∴OH=BF,∠DOH=∠CBD=45°,
∵OH是△BFD的中位线,
∴DG=CG=BC,GH=CF,
∵CE=CF,
∴GH=CF=CE
∵CE<CG=BC,
∴GH<BC,故②错误.
∵四边形ABCD是正方形,BE是∠DBC的平分线,
∴BC=CD,∠BCD=∠DCF,∠EBC=22.5°,
∵CE=CF,
∴Rt△BCE≌Rt△DCF(SAS),
∴∠EBC=∠CDF=22.5°,
∴∠BFH=90°﹣∠CDF=90°﹣22.5°=67.5°,
∵OH是△DBF的中位线,CD⊥AF,
∴OH是CD的垂直平分线,
∴DH=CH,
∴∠CDF=∠DCH=22.5°,
∴∠HCF=90°﹣∠DCH=90°﹣22.5°=67.5°,
∴∠CHF=180°﹣∠HCF﹣∠BFH=180°﹣67.5°﹣67.5°=45°,故④正确;
∴∠ODH=∠BDC+∠CDF=67.5°,
∴∠OHD=180°﹣∠ODH﹣∠DOH=67.5°,
∴∠ODH=∠OHD,
∴OD=OH=BF;故③正确.
故选:B.
11.解:∵四边形ABCD是正方形,且AC为正方ABCD的对角线,
∴△ABE与△ADE关于直线AC对称,∠ACB=45°,
∴∠AED=∠AEB,
∵∠AEB为△EBC的外角,
∴∠AEB=∠CBE+∠ACB=25°+45°=70°,
∴∠AED=70°,
故答案为70.
12.解:∵四边形ABCD是正方形,
∴AB=CD,∠BAD=90°,∠ADB=45°,
∵∠DAE=67.5°,
∴∠EAD=180°﹣45°﹣67.5°=67.5°,
∴AD=DE=1,
在Rt△ABD中,AB=AD=1,
∴AC==,
故答案为.
13.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵∠OBC=∠OCB,
∴OB=OC,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:AB=AD(答案不唯一).
理由:∵四边形ABCD是矩形,
又∵AB=AD,
∴四边形ABCD是正方形.
14.(1)证明:∵AC⊥BD,DF⊥DB,
∴AC∥DF,
∵AD∥BC,
∴四边形ACFD是平行四边形,
∴AD=CF;
(2)证明:∵点C为BF中点,
∴BC=CF,
∵AD=CF,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵DF⊥DB,BC=CF,
∴DC=BC=BF,
∴四边形ABCD是菱形;
(3)解:当△BDF满足是等腰三角形时(BD=DF),四边形ABCD是正方形.
证明:∵DF⊥DB,
∴∠BDF=90°,
∵BD=DF,
∴∠DBF=∠DFB=(180°﹣∠BDF)=×(180°﹣90°)=45°,
由(2)知,四边形ABCD是菱形,
∴∠ABD=∠DBF=45°,
∴∠ABC=∠ABD+∠DBF=45°+45°=90°,
∵四边形ABCD是菱形,
∴四边形ABCD是正方形.
15.解:(1)∵四边形ABCD是正方形,
∴OA=OB,∠DAO=45°,∠OBA=45°,
∴∠OAM=∠OBN=135°,
∵∠EOF=90°,∠AOB=90°,
∴∠AOM=∠BON,
∴△OAM≌△OBN(ASA),
∴OM=ON;
(2)如图,过点O作OH⊥AD于点H,
∵正方形的边长为6,
∴OH=HA=3,
∵E为OM的中点,
∴HM=6,
则OM==3,
∴MN=OM=3.
16.(1)证明:∵四边形ADEF和四边形ABHG都是正方形,
∴AD=AF,AB=AG,∠BAG=∠DAF=90°,
∴∠GAF+∠BAD=180°,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAD+∠ADC=180°,
∴∠GAF=∠ADC,
在△AFG和△DAC中,
,
∴△AFG≌△DAC(SAS),
∴GF=AC,
∵平行四边形ABCD中,AC=2AO,
∴GF=2AO;
(2)解:过点D作DM⊥AB于点M,
∵AD=4,∠BAD=60°,∠AMD=90°,
∴DM=4×sin60°=4×=2,
∴S平行四边形ABCD=AB?DM=6×2=12,
∴S△DAC=,
∵△AFG≌△DAC,
∴S△DAC=S△AGF=6.
即△AGF的面积为6.
17.证明:(1)∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD=45°,∠C=90°,
在△ABP与△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC;
(2)∵PE⊥CD,PF⊥BC,
∴∠PFC=90°,∠PEC=90°.
又∵∠BCD=90°,
∴四边形PFCE是矩形,
∴EC=PF,PE=CF,
∵∠CBD=45°,∠PFB=90°,
∴BF=PF,
又∵BC=1,
∴矩形PFCE的周长为2(PF+FC)=2(BF+FC)=2BC=2.
18.证明:(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠C=∠ADC=∠DAB=90°,
如图①:延长BA,使AM=CF,连接MD,
在△AMD和△CFD中,
,
∴△AMD≌△CFD(SAS),
∴∠MDA=∠CDF,MD=DF,
∵∠EDF=45°,
∴∠ADE+∠FDC=45°,
∴∠ADM+∠ADE=45°=∠MDE,
∴∠MDE=∠EDF,
在△EDF和△EDM中,
,
∴△EDF≌△EDM(SAS),
∴EF=EM,
∵EM=AM+AE=AE+CF,
∴EF=AE+CF;
(2)EF2=AE2+CF2,
理由如下:
如图②,将△CDF绕点D顺时针旋转90°,可得△ADN,
由旋转的性质可得DN=DF,AN=CF,∠DAN=∠DCF=45°,∠CDF=∠ADN,
∴∠CAN=∠CAD+∠DAN=90°,
∴EN2=AE2+AN2,
∵∠EDF=45°,
∴∠CDF+∠ADE=45°,
∴∠ADE+∠ADN=45°=∠NDE=∠EDF,
在△EDF和△EDN中,
,
∴△EDF≌△EDN(SAS),
∴EF=EN,
∴EF2=AE2+CF2.
19.解:(1)∵四边形ABCD是正方形,
∴AD=AB=2,BD=AD=2,∠ABD=∠CBD=45°,
∴BE=BD﹣DE=2﹣1,
∵EG⊥BD,∠DBG=45°,
∴∠DBG=∠EGB=45°,
∴EB=EG=2﹣1;
(2)∵AE⊥EF,
∴∠AEF=∠BEG=90°,
∴∠AEB=∠GEF,
又∵BE=EG,∠ABD=∠FGE=45°,
∴△ABE≌△FGE(AAS),
∴FG=AB.
20.证明:(1)∵AF=AD,AE⊥DF,
∴∠DAE=∠EAF=∠DAF,
∵AF平分∠EAF,
∴∠BAG=∠FAG=∠BAF,
∵∠GAE=∠EAF﹣∠FAG=(∠DAF﹣∠BAF),
∴∠GAE=45°,
∴∠GAE=∠AGE=45°,
∴AE=GE;
(2)如图,过点C作CH⊥DF于H,
∴∠AED=∠CHD=90°,
∴∠ADE+∠EAD=90°=∠ADE+∠CDH,
∴∠EAD=∠CDH,
在△ADE和△DCH中,
,
∴△ADE≌△DCH(AAS),
∴CH=DE,DH=AE=GE,
∴DE=GH=CH,
∴GC=CH=DE.
21.(1)证明:∵四边形ABCD和四边形BEFG是正方形,
∴∠BAD=∠FGB=90°,AB=AD,
∵DM⊥AG,
∴∠DMA=∠AGB=90°,
∵∠DAM+∠GAB=90°,∠DAM+∠ADM=90°,
∴∠ADM=∠GAB,
∴△ABG≌△DAM(AAS);
(2)解:在Rt△ABG中,AG==12,
∵△ABG≌△DAM,
∴DM=AG=12,AM=BG=9,
∴MG=AG﹣AM=3,
在Rt△DMG中,DG==3;
(3)解:∵四边形ABCD和四边形BEFG是正方形,
∴∠ABC=∠GBE=90°,AB=BC,
∴∠ABG=∠CBE,
∴△ABG≌△CBE(SAS),
∴S△ABG=S△CBE,
∵S△ABH﹣S△CHF=S△ABH+S四边形BHFE﹣(S△CHF+S四边形HFEB)=S△ABG+S正方形GBFE﹣S△CBE=S正方形BGFE=92=81,
∴△ABH与△CFH的面积差为81.
22.证明:(1)∵四边形ABCD是正方形,
∴BC=CD=AD=AB,∠BCD=∠ADC=90°,
∵BM⊥CE,
∴∠HMC=∠ADC=90°,
∴∠H+∠HCM=90°=∠E+∠ECD,
∴∠H=∠E,
在△EDC和△HCB中,
,
∴△EDC≌△HCB(AAS),
∴CE=BH;
(2)△BCG,△DCF,△DHF,△ABF,
理由如下:∵AE=AB,
∴AE=BC=AD=CD,
∵△EDC≌△HCB,
∴ED=HC,
∵AD=CD,
∴AE=HD=CD=AB,
在△AEG和△BCG中,
,
∴△AEG≌△BCG(AAS),
∴AG=BG=AB,
同理可证△AFB≌△DFH,
∴AF=DF=AD,
∴AG=AF=DF,
在△AEG和△ABF中,
,
∴△AEG≌△ABF(SAS),
同理可证△AEG≌△DHF,△AEG≌△DCF.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
