4.1 函数年同步练习 2020-2021 学年北师大版 八年级数学上册 (word版含解析)
文档属性
| 名称 | 4.1 函数年同步练习 2020-2021 学年北师大版 八年级数学上册 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 169.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 07:46:40 | ||
图片预览




文档简介
4.1
函数
一、选择题
1.下列图形中的图象不表示y是x的函数的是( )
A.
B.
C.
D.
2从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是( )
A.物体
B.速度
C.时间
D.空气
3在下表中,设x表示乘公共汽车的站数,y表示应付的票价(元)
x(站)
1
2
3
4
5
6
7
8
9
10
y(元)
1
1
1
2
2
3
3
3
4
4
根据此表,下列说法正确的是( )
A.y是x的函数
B.y不是x的函数
C.x是y的函数
D.以上说法都不对
4函数自变量x的取值范围是( )
A.x≥1且x≠3
B.x≥1
C.x≠3
D.x>1且x≠3
5下列是关于变量x和y的四个关系式:①y=x;②y2=x;③2x2=y;④y2=2x.其中y是x的函数有( )
A.1个
B.2个
C.3个
D.4个
6据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是
( )
A.y=0.05x
B.y=5x
C.y=100x
D.y=0.05x+100
7已知等腰三角形的周长为10cm,将底边长ycm表示为腰长xcm的关系式是y=10﹣2x,则其自变量x的取值范围是( )
A.0<x<5
B.2.5<x<5
C.一切实数
D.x>0
8弹簧挂上物体会伸长,测得一弹簧的长度x(cm)与所挂的物体的重量y(kg)间的关系如下表:
x
0
1
2
3
4
5
6
y
10
10.5
11
11.5
12
12.5
13
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂物体时的长度为0cm
C.物体质量每增加1kg,弹簧的长度y增加0.5cm
D.所挂的物体的质量为7kg时,弹簧的长度为13.5cm
9若函数,则当函数值y=8时,自变量x的值是( )
A.±
B.4
C.±或4
D.4或﹣
二、填空题
10一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的 ,其中x是 ,y是 .
11小明到商店买练习簿,每本单价2元,购买的总数x(本)与总金额y(元)的关系式可以表示为 ,其中变量是 ,常量是 .
12飞船每分钟转30转,用函数解析式表示转数n和时间t之间的关系式是 .
13在函数y=中,自变量x的取值范围是
.
14林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中 是常量, 是变量.
15小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发xmin后行走的路程为ym.图中的折线表示小明在整个行走过程中y与x的函数关系.
(1)小明行走的总路程是 m,他途中休息了 min;
(2)当小丽到达缆车终点时,小明离缆车终点的路程是 m.
三、解答题
16求下列函数中自变量x的取值范围.
(1)y=3x﹣1;
(2)y=2x2+7;
(3)y=;
(4)y=.
17“十一”期间,小华约同学一起开车到距家100千米的景点旅游,出发前,汽车油箱内储油35升,当行驶80千米时,发现油箱余油量为25升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=60(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
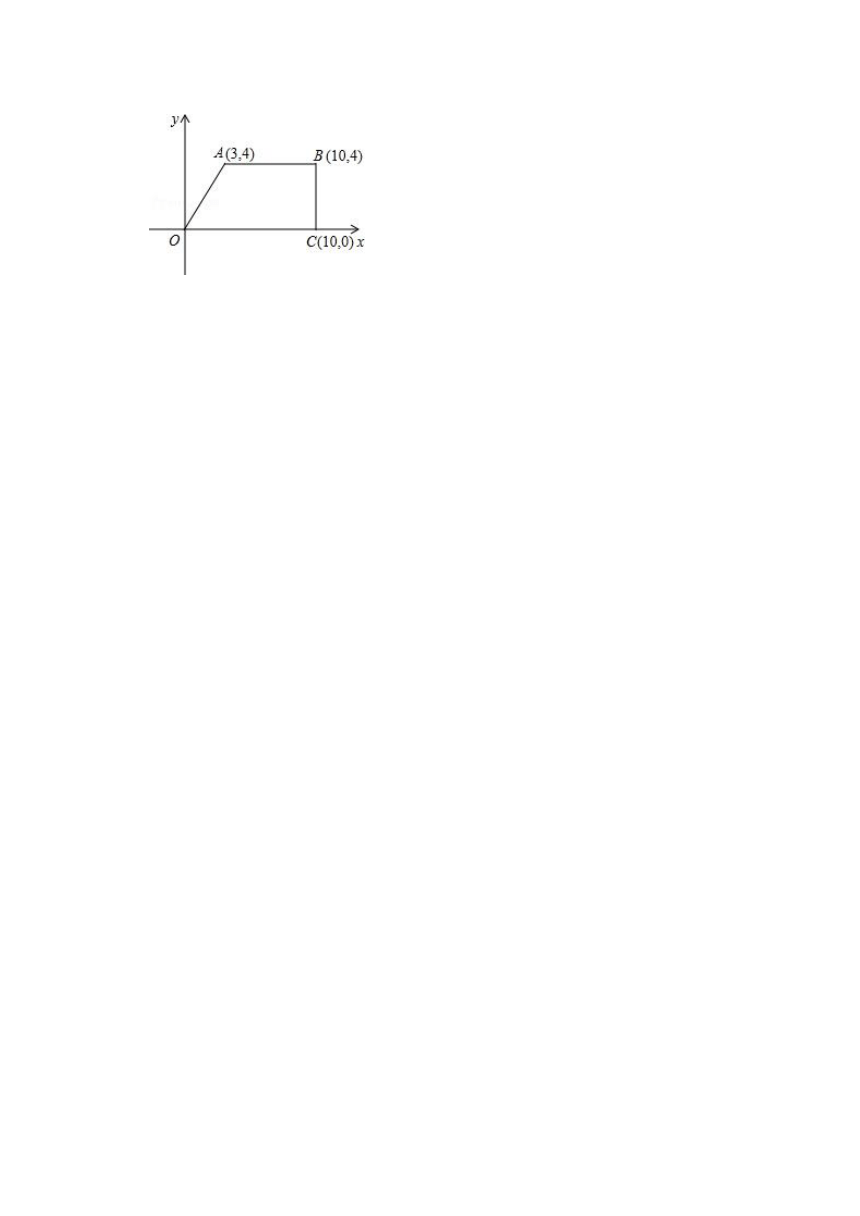
18如图所示,在四边形OABC中,A(3,4)、B(10,4),C(10,0)点P沿A→B→C的路线以每秒2个单位长度的速度运动,设运动的时间为t秒.
(1)分别写出点P在线段AB或在线段BC上的坐标(用含t的代数式表示)及t的取值范围;
(2)当S△AOP=时,求出t的值.
4.1
函数
一、选择题
1.下列图形中的图象不表示y是x的函数的是( )
A.
B.
C.
D.
【考点】函数的概念;函数的图象.
【专题】函数及其图象.
【答案】D
【分析】运用函数的定义,x取一个值,y有唯一值对应,可直接得出答案.
【解答】解:A、根据图象知给自变量一个值,有且只有一个函数值与其对应,故A是函数,
B、根据图象知给自变量一个值,有且只有1个函数值与其对应,故B是函数,
C、根据图象知给自变量一个值,有且只有1个函数值与其对应,故C是函数,
D、根据图象知给自变量一个值,有3个函数值与其对应,故D不是函数,
故选:D.
2从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是( )
A.物体
B.速度
C.时间
D.空气
【考点】常量与变量.
【答案】C
【分析】根据函数的定义解答.
【解答】解:因为速度随时间的变化而变化,
故时间是自变量,速度是因变量,
即速度是时间的函数.
故选:C.
3在下表中,设x表示乘公共汽车的站数,y表示应付的票价(元)
x(站)
1
2
3
4
5
6
7
8
9
10
y(元)
1
1
1
2
2
3
3
3
4
4
根据此表,下列说法正确的是( )
A.y是x的函数
B.y不是x的函数
C.x是y的函数
D.以上说法都不对
【考点】函数的概念.
【专题】常规题型.
【答案】A
【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可得出正确答案.
【解答】解:根据题意:对于x的每一个取值,y都有唯一确定的值,
故y是x的函数.
故选:A.
4函数自变量x的取值范围是( )
A.x≥1且x≠3
B.x≥1
C.x≠3
D.x>1且x≠3
【考点】函数自变量的取值范围.
【答案】A
【分析】根据被开方数大于等于0,分母不等于0列式进行计算即可得解.
【解答】解:根据题意得,x﹣1≥0且x﹣3≠0,
解得x≥1且x≠3.
故选:A.
5下列是关于变量x和y的四个关系式:①y=x;②y2=x;③2x2=y;④y2=2x.其中y是x的函数有( )
A.1个
B.2个
C.3个
D.4个
【考点】函数的概念.
【答案】B
【分析】根据函数的定义:对于x的每一个取值,y都有唯一确定的值与之对应即可确定有几个函数.
【解答】解:是函数的有:
①y=x;③2x2=y.
故选:B.
6据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是
( )
A.y=0.05x
B.y=5x
C.y=100x
D.y=0.05x+100
【考点】函数关系式.
【专题】模型思想;应用意识.
【答案】B
【分析】每分钟滴出100滴水,每滴水约0.05毫升,则一分钟滴水100×0.05毫升,则x分钟可滴100×0.05x毫升,据此即可求解.
【解答】解:y=100×0.05x,
即y=5x.
故选:B.
7已知等腰三角形的周长为10cm,将底边长ycm表示为腰长xcm的关系式是y=10﹣2x,则其自变量x的取值范围是( )
A.0<x<5
B.2.5<x<5
C.一切实数
D.x>0
【考点】函数自变量的取值范围.
【答案】B
【分析】根据三角形两边之和大于第三边及周长的限制,确定自变量的取值范围.
【解答】解:根据三角形的三边关系得:
,
解得:2.5<x<5.
故选:B.
8弹簧挂上物体会伸长,测得一弹簧的长度x(cm)与所挂的物体的重量y(kg)间的关系如下表:
x
0
1
2
3
4
5
6
y
10
10.5
11
11.5
12
12.5
13
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂物体时的长度为0cm
C.物体质量每增加1kg,弹簧的长度y增加0.5cm
D.所挂的物体的质量为7kg时,弹簧的长度为13.5cm
【考点】常量与变量;函数关系式;函数值.
【答案】B
【分析】由表中的数据进行分析发现:物体质量每增加1kg,弹簧长度y增加0.5cm;当不挂重物时,弹簧的长度为10cm,然后逐个分析四个选项,得出正确答案.
【解答】解:A、y随x的增加而增加,x是自变量,y是因变量,故A选项正确;
B、弹簧不挂重物时的长度为10cm,故B选项错误;
C、物体质量每增加1kg,弹簧长度y增加0.5cm,故C选项正确;
D、由C知,y=10+0.5x,则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故D选项正确.
故选:B.
9若函数,则当函数值y=8时,自变量x的值是( )
A.±
B.4
C.±或4
D.4或﹣
【考点】函数值.
【专题】计算题.
【答案】D
【分析】把y=8直接代入函数即可求出自变量的值.
【解答】解:把y=8代入函数,
先代入上边的方程得x=,
∵x≤2,x=不合题意舍去,故x=﹣;
再代入下边的方程x=4,
∵x>2,故x=4,
综上,x的值为4或﹣.
故选:D.
二、填空题
10一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的 ,其中x是 ,y是 .
【考点】函数的概念.
【专题】函数及其图象;数感.
【答案】函数,自变量,因变量.
【分析】根据函数的定义进行解答.
【解答】解:一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
故答案为:函数,自变量,因变量.
11小明到商店买练习簿,每本单价2元,购买的总数x(本)与总金额y(元)的关系式可以表示为 ,其中变量是 ,常量是 .
【考点】常量与变量;函数关系式.
【专题】销售问题.
【答案】见试题解答内容
【分析】总金额等于每个练习薄的价格乘以购买的总数,则y=2x(x为自然数),然后根据变量与常量的定义常量,变量.
【解答】解:关系式是:y=2x(x为自然数),其中2为常量,x和y为变量.
故答案为y=2x(n为自然数);x和y;2.
12飞船每分钟转30转,用函数解析式表示转数n和时间t之间的关系式是 .
【考点】函数关系式.
【专题】计算题.
【答案】见试题解答内容
【分析】由飞船每分钟转30转,可知当t=1时,n=30,由此本题可容易解出.
【解答】解:∵飞船每分钟转30转,
∵T=1时,n=30,
T=2时,n=2×30,
T=3时,n=3×30,
…
T=t时,n=t×30,
故答案为:n=30t.
13在函数y=中,自变量x的取值范围是
.
【考点】分式有意义的条件;函数自变量的取值范围.
【专题】计算题.
【答案】见试题解答内容
【分析】求函数自变量的取值范围,就是求函数解析式有意义的条件,分式有意义的条件是:分母不为0.
【解答】解:要使分式有意义,即:x﹣2≠0,
解得:x≠2.
故答案为:x≠2.
14林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中 是常量, 是变量.
【考点】常量与变量.
【答案】见试题解答内容
【分析】常量就是在变化过程中不变的量,变量是指在程序的运行过程中随时可以发生变化的量.
【解答】解:在这三个量当中元/升是常量,数量、金额是变量.
15小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发xmin后行走的路程为ym.图中的折线表示小明在整个行走过程中y与x的函数关系.
(1)小明行走的总路程是 m,他途中休息了 min;
(2)当小丽到达缆车终点时,小明离缆车终点的路程是 m.
【考点】函数的图象.
【答案】见试题解答内容
【分析】(1)观察函数图象,即可得出小明行走的总路程以及途中休息的时间;
(2)根据时间=路程÷速度可求出小丽乘坐缆车需要的时间,设小明在60≤x≤90段的y关于x的函数关系式为y=kx+b,根据图中点的坐标利用待定系数法即可求出该时间段y关于x的函数关系式,代入x=70即可求出y值,再用总路程减去该值即可得出结论.
【解答】解:(1)根据图形可得出:小明行走的总路程是3800m;途中休息时间为60﹣30=30(min).
故答案为:3800;30.
(2)小丽到达缆车终点的时间为3800÷2÷190+60=70(min),
设小明在60≤x≤90段的y关于x的函数关系式为y=kx+b,
将(60,2000)、(90,3800)代入y=kx+b中,得:
,解得:,
∴小明在60≤x≤90段的y关于x的函数关系式为y=60x﹣1600.
当x=70时,y=60×70﹣1600=2600,
此时小明离缆车终点的路程是3800﹣2600=1200(m).
故答案为:1200.
三、解答题
16求下列函数中自变量x的取值范围.
(1)y=3x﹣1;
(2)y=2x2+7;
(3)y=;
(4)y=.
【考点】函数自变量的取值范围.
【答案】见试题解答内容
【分析】(1)根据一次函数的自变量的取值范围是全体实数,可得答案;
(2)根据二次函数的自变量的取值范围是全体实数,可得答案;
(3)根据分母不能为零,可得函数自变量的取值范围;
(4)根据二次根式的被开方数是非负数,可得函数自变量的取值范围.
【解答】解:(1)y=3x﹣1自变量的取值范围是全体实数;
(2)y=2x2+7自变量的取值范围是全体实数;
(3)y=自变量的取值范围是x+2≠0,解得x≠﹣2,
(4)y=自变量的取值范围是x﹣2≥0,解得x≥2.
17“十一”期间,小华约同学一起开车到距家100千米的景点旅游,出发前,汽车油箱内储油35升,当行驶80千米时,发现油箱余油量为25升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=60(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
【考点】函数关系式.
【专题】函数及其图象.
【答案】见试题解答内容
【分析】(1)单位耗油量=耗油量÷行驶里程,剩余油量=油箱内油的升数﹣行驶路程的耗油量;
(2)把x=60千米代入剩余油量公式,计算即可;
(3)计算出35﹣3=32升油能行驶的距离,与200千米比较大小即可得.
【解答】解:(1)该汽车平均每千米的耗油量为(35﹣25)÷80=0.125(升/千米),
∴行驶路程x(千米)与剩余油量Q(升)的关系式为Q=35﹣0.125x;
(2)当x=60时,Q=35﹣0.125×60=27.5(升),
答:当x=60(千米)时,剩余油量Q的值为27.5升;
(3)他们能在汽车报警前回到家,
(35﹣3)÷0.125=256(千米),
由256>200知他们能在汽车报警前回到家.
18如图所示,在四边形OABC中,A(3,4)、B(10,4),C(10,0)点P沿A→B→C的路线以每秒2个单位长度的速度运动,设运动的时间为t秒.
(1)分别写出点P在线段AB或在线段BC上的坐标(用含t的代数式表示)及t的取值范围;
(2)当S△AOP=时,求出t的值.
【考点】坐标与图形性质;三角形的面积;四边形;轨迹.
【专题】代数几何综合题;四边形;运算能力;推理能力.
【答案】(1)点P坐标为(3+2t,4)(0≤t≤)或(10,11﹣2t)();
(2)t=.
【分析】(1)分别对点P在AB上或者BC上进行讨论,当点在AB上时,其纵坐标为4;点P在BC上时,其横坐标为10,再根据点P的运动规律求解即可;
(2)分点P在AB或BC上两种情况进行讨论求解即可.
【解答】解:(1)当点P在AB上运动时,PA=2t,
点P坐标为(3+2t,4)(0≤t≤);
当点P在BC上运动时,PB=2t﹣7,PC=BC﹣PB=4﹣(2t﹣7)=11﹣2t,
点P坐标为(10,11﹣2t)().
(2)∵S四边形OABC==34.
∴S△AOP=S四边形OABC=17.
①当P在AB上时,
S△AOP=AP?4=4t=17,解得:t=>(不符合题意,舍去).
②当P在BC上时,若S△AOP=17,
则S△ABP+S△OCP=(AB?BP+OC?CP)=[7×(2t﹣7)+10×(11﹣2t)]=17.
解得:t=(符合题意).
综上所述,t=.
函数
一、选择题
1.下列图形中的图象不表示y是x的函数的是( )
A.
B.
C.
D.
2从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是( )
A.物体
B.速度
C.时间
D.空气
3在下表中,设x表示乘公共汽车的站数,y表示应付的票价(元)
x(站)
1
2
3
4
5
6
7
8
9
10
y(元)
1
1
1
2
2
3
3
3
4
4
根据此表,下列说法正确的是( )
A.y是x的函数
B.y不是x的函数
C.x是y的函数
D.以上说法都不对
4函数自变量x的取值范围是( )
A.x≥1且x≠3
B.x≥1
C.x≠3
D.x>1且x≠3
5下列是关于变量x和y的四个关系式:①y=x;②y2=x;③2x2=y;④y2=2x.其中y是x的函数有( )
A.1个
B.2个
C.3个
D.4个
6据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是
( )
A.y=0.05x
B.y=5x
C.y=100x
D.y=0.05x+100
7已知等腰三角形的周长为10cm,将底边长ycm表示为腰长xcm的关系式是y=10﹣2x,则其自变量x的取值范围是( )
A.0<x<5
B.2.5<x<5
C.一切实数
D.x>0
8弹簧挂上物体会伸长,测得一弹簧的长度x(cm)与所挂的物体的重量y(kg)间的关系如下表:
x
0
1
2
3
4
5
6
y
10
10.5
11
11.5
12
12.5
13
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂物体时的长度为0cm
C.物体质量每增加1kg,弹簧的长度y增加0.5cm
D.所挂的物体的质量为7kg时,弹簧的长度为13.5cm
9若函数,则当函数值y=8时,自变量x的值是( )
A.±
B.4
C.±或4
D.4或﹣
二、填空题
10一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的 ,其中x是 ,y是 .
11小明到商店买练习簿,每本单价2元,购买的总数x(本)与总金额y(元)的关系式可以表示为 ,其中变量是 ,常量是 .
12飞船每分钟转30转,用函数解析式表示转数n和时间t之间的关系式是 .
13在函数y=中,自变量x的取值范围是
.
14林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中 是常量, 是变量.
15小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发xmin后行走的路程为ym.图中的折线表示小明在整个行走过程中y与x的函数关系.
(1)小明行走的总路程是 m,他途中休息了 min;
(2)当小丽到达缆车终点时,小明离缆车终点的路程是 m.
三、解答题
16求下列函数中自变量x的取值范围.
(1)y=3x﹣1;
(2)y=2x2+7;
(3)y=;
(4)y=.
17“十一”期间,小华约同学一起开车到距家100千米的景点旅游,出发前,汽车油箱内储油35升,当行驶80千米时,发现油箱余油量为25升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=60(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
18如图所示,在四边形OABC中,A(3,4)、B(10,4),C(10,0)点P沿A→B→C的路线以每秒2个单位长度的速度运动,设运动的时间为t秒.
(1)分别写出点P在线段AB或在线段BC上的坐标(用含t的代数式表示)及t的取值范围;
(2)当S△AOP=时,求出t的值.
4.1
函数
一、选择题
1.下列图形中的图象不表示y是x的函数的是( )
A.
B.
C.
D.
【考点】函数的概念;函数的图象.
【专题】函数及其图象.
【答案】D
【分析】运用函数的定义,x取一个值,y有唯一值对应,可直接得出答案.
【解答】解:A、根据图象知给自变量一个值,有且只有一个函数值与其对应,故A是函数,
B、根据图象知给自变量一个值,有且只有1个函数值与其对应,故B是函数,
C、根据图象知给自变量一个值,有且只有1个函数值与其对应,故C是函数,
D、根据图象知给自变量一个值,有3个函数值与其对应,故D不是函数,
故选:D.
2从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是( )
A.物体
B.速度
C.时间
D.空气
【考点】常量与变量.
【答案】C
【分析】根据函数的定义解答.
【解答】解:因为速度随时间的变化而变化,
故时间是自变量,速度是因变量,
即速度是时间的函数.
故选:C.
3在下表中,设x表示乘公共汽车的站数,y表示应付的票价(元)
x(站)
1
2
3
4
5
6
7
8
9
10
y(元)
1
1
1
2
2
3
3
3
4
4
根据此表,下列说法正确的是( )
A.y是x的函数
B.y不是x的函数
C.x是y的函数
D.以上说法都不对
【考点】函数的概念.
【专题】常规题型.
【答案】A
【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可得出正确答案.
【解答】解:根据题意:对于x的每一个取值,y都有唯一确定的值,
故y是x的函数.
故选:A.
4函数自变量x的取值范围是( )
A.x≥1且x≠3
B.x≥1
C.x≠3
D.x>1且x≠3
【考点】函数自变量的取值范围.
【答案】A
【分析】根据被开方数大于等于0,分母不等于0列式进行计算即可得解.
【解答】解:根据题意得,x﹣1≥0且x﹣3≠0,
解得x≥1且x≠3.
故选:A.
5下列是关于变量x和y的四个关系式:①y=x;②y2=x;③2x2=y;④y2=2x.其中y是x的函数有( )
A.1个
B.2个
C.3个
D.4个
【考点】函数的概念.
【答案】B
【分析】根据函数的定义:对于x的每一个取值,y都有唯一确定的值与之对应即可确定有几个函数.
【解答】解:是函数的有:
①y=x;③2x2=y.
故选:B.
6据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是
( )
A.y=0.05x
B.y=5x
C.y=100x
D.y=0.05x+100
【考点】函数关系式.
【专题】模型思想;应用意识.
【答案】B
【分析】每分钟滴出100滴水,每滴水约0.05毫升,则一分钟滴水100×0.05毫升,则x分钟可滴100×0.05x毫升,据此即可求解.
【解答】解:y=100×0.05x,
即y=5x.
故选:B.
7已知等腰三角形的周长为10cm,将底边长ycm表示为腰长xcm的关系式是y=10﹣2x,则其自变量x的取值范围是( )
A.0<x<5
B.2.5<x<5
C.一切实数
D.x>0
【考点】函数自变量的取值范围.
【答案】B
【分析】根据三角形两边之和大于第三边及周长的限制,确定自变量的取值范围.
【解答】解:根据三角形的三边关系得:
,
解得:2.5<x<5.
故选:B.
8弹簧挂上物体会伸长,测得一弹簧的长度x(cm)与所挂的物体的重量y(kg)间的关系如下表:
x
0
1
2
3
4
5
6
y
10
10.5
11
11.5
12
12.5
13
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂物体时的长度为0cm
C.物体质量每增加1kg,弹簧的长度y增加0.5cm
D.所挂的物体的质量为7kg时,弹簧的长度为13.5cm
【考点】常量与变量;函数关系式;函数值.
【答案】B
【分析】由表中的数据进行分析发现:物体质量每增加1kg,弹簧长度y增加0.5cm;当不挂重物时,弹簧的长度为10cm,然后逐个分析四个选项,得出正确答案.
【解答】解:A、y随x的增加而增加,x是自变量,y是因变量,故A选项正确;
B、弹簧不挂重物时的长度为10cm,故B选项错误;
C、物体质量每增加1kg,弹簧长度y增加0.5cm,故C选项正确;
D、由C知,y=10+0.5x,则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故D选项正确.
故选:B.
9若函数,则当函数值y=8时,自变量x的值是( )
A.±
B.4
C.±或4
D.4或﹣
【考点】函数值.
【专题】计算题.
【答案】D
【分析】把y=8直接代入函数即可求出自变量的值.
【解答】解:把y=8代入函数,
先代入上边的方程得x=,
∵x≤2,x=不合题意舍去,故x=﹣;
再代入下边的方程x=4,
∵x>2,故x=4,
综上,x的值为4或﹣.
故选:D.
二、填空题
10一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的 ,其中x是 ,y是 .
【考点】函数的概念.
【专题】函数及其图象;数感.
【答案】函数,自变量,因变量.
【分析】根据函数的定义进行解答.
【解答】解:一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
故答案为:函数,自变量,因变量.
11小明到商店买练习簿,每本单价2元,购买的总数x(本)与总金额y(元)的关系式可以表示为 ,其中变量是 ,常量是 .
【考点】常量与变量;函数关系式.
【专题】销售问题.
【答案】见试题解答内容
【分析】总金额等于每个练习薄的价格乘以购买的总数,则y=2x(x为自然数),然后根据变量与常量的定义常量,变量.
【解答】解:关系式是:y=2x(x为自然数),其中2为常量,x和y为变量.
故答案为y=2x(n为自然数);x和y;2.
12飞船每分钟转30转,用函数解析式表示转数n和时间t之间的关系式是 .
【考点】函数关系式.
【专题】计算题.
【答案】见试题解答内容
【分析】由飞船每分钟转30转,可知当t=1时,n=30,由此本题可容易解出.
【解答】解:∵飞船每分钟转30转,
∵T=1时,n=30,
T=2时,n=2×30,
T=3时,n=3×30,
…
T=t时,n=t×30,
故答案为:n=30t.
13在函数y=中,自变量x的取值范围是
.
【考点】分式有意义的条件;函数自变量的取值范围.
【专题】计算题.
【答案】见试题解答内容
【分析】求函数自变量的取值范围,就是求函数解析式有意义的条件,分式有意义的条件是:分母不为0.
【解答】解:要使分式有意义,即:x﹣2≠0,
解得:x≠2.
故答案为:x≠2.
14林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中 是常量, 是变量.
【考点】常量与变量.
【答案】见试题解答内容
【分析】常量就是在变化过程中不变的量,变量是指在程序的运行过程中随时可以发生变化的量.
【解答】解:在这三个量当中元/升是常量,数量、金额是变量.
15小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发xmin后行走的路程为ym.图中的折线表示小明在整个行走过程中y与x的函数关系.
(1)小明行走的总路程是 m,他途中休息了 min;
(2)当小丽到达缆车终点时,小明离缆车终点的路程是 m.
【考点】函数的图象.
【答案】见试题解答内容
【分析】(1)观察函数图象,即可得出小明行走的总路程以及途中休息的时间;
(2)根据时间=路程÷速度可求出小丽乘坐缆车需要的时间,设小明在60≤x≤90段的y关于x的函数关系式为y=kx+b,根据图中点的坐标利用待定系数法即可求出该时间段y关于x的函数关系式,代入x=70即可求出y值,再用总路程减去该值即可得出结论.
【解答】解:(1)根据图形可得出:小明行走的总路程是3800m;途中休息时间为60﹣30=30(min).
故答案为:3800;30.
(2)小丽到达缆车终点的时间为3800÷2÷190+60=70(min),
设小明在60≤x≤90段的y关于x的函数关系式为y=kx+b,
将(60,2000)、(90,3800)代入y=kx+b中,得:
,解得:,
∴小明在60≤x≤90段的y关于x的函数关系式为y=60x﹣1600.
当x=70时,y=60×70﹣1600=2600,
此时小明离缆车终点的路程是3800﹣2600=1200(m).
故答案为:1200.
三、解答题
16求下列函数中自变量x的取值范围.
(1)y=3x﹣1;
(2)y=2x2+7;
(3)y=;
(4)y=.
【考点】函数自变量的取值范围.
【答案】见试题解答内容
【分析】(1)根据一次函数的自变量的取值范围是全体实数,可得答案;
(2)根据二次函数的自变量的取值范围是全体实数,可得答案;
(3)根据分母不能为零,可得函数自变量的取值范围;
(4)根据二次根式的被开方数是非负数,可得函数自变量的取值范围.
【解答】解:(1)y=3x﹣1自变量的取值范围是全体实数;
(2)y=2x2+7自变量的取值范围是全体实数;
(3)y=自变量的取值范围是x+2≠0,解得x≠﹣2,
(4)y=自变量的取值范围是x﹣2≥0,解得x≥2.
17“十一”期间,小华约同学一起开车到距家100千米的景点旅游,出发前,汽车油箱内储油35升,当行驶80千米时,发现油箱余油量为25升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=60(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
【考点】函数关系式.
【专题】函数及其图象.
【答案】见试题解答内容
【分析】(1)单位耗油量=耗油量÷行驶里程,剩余油量=油箱内油的升数﹣行驶路程的耗油量;
(2)把x=60千米代入剩余油量公式,计算即可;
(3)计算出35﹣3=32升油能行驶的距离,与200千米比较大小即可得.
【解答】解:(1)该汽车平均每千米的耗油量为(35﹣25)÷80=0.125(升/千米),
∴行驶路程x(千米)与剩余油量Q(升)的关系式为Q=35﹣0.125x;
(2)当x=60时,Q=35﹣0.125×60=27.5(升),
答:当x=60(千米)时,剩余油量Q的值为27.5升;
(3)他们能在汽车报警前回到家,
(35﹣3)÷0.125=256(千米),
由256>200知他们能在汽车报警前回到家.
18如图所示,在四边形OABC中,A(3,4)、B(10,4),C(10,0)点P沿A→B→C的路线以每秒2个单位长度的速度运动,设运动的时间为t秒.
(1)分别写出点P在线段AB或在线段BC上的坐标(用含t的代数式表示)及t的取值范围;
(2)当S△AOP=时,求出t的值.
【考点】坐标与图形性质;三角形的面积;四边形;轨迹.
【专题】代数几何综合题;四边形;运算能力;推理能力.
【答案】(1)点P坐标为(3+2t,4)(0≤t≤)或(10,11﹣2t)();
(2)t=.
【分析】(1)分别对点P在AB上或者BC上进行讨论,当点在AB上时,其纵坐标为4;点P在BC上时,其横坐标为10,再根据点P的运动规律求解即可;
(2)分点P在AB或BC上两种情况进行讨论求解即可.
【解答】解:(1)当点P在AB上运动时,PA=2t,
点P坐标为(3+2t,4)(0≤t≤);
当点P在BC上运动时,PB=2t﹣7,PC=BC﹣PB=4﹣(2t﹣7)=11﹣2t,
点P坐标为(10,11﹣2t)().
(2)∵S四边形OABC==34.
∴S△AOP=S四边形OABC=17.
①当P在AB上时,
S△AOP=AP?4=4t=17,解得:t=>(不符合题意,舍去).
②当P在BC上时,若S△AOP=17,
则S△ABP+S△OCP=(AB?BP+OC?CP)=[7×(2t﹣7)+10×(11﹣2t)]=17.
解得:t=(符合题意).
综上所述,t=.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
