2021-2022学年北师大版七年级数学上册1.1.1认识几何体同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学上册1.1.1认识几何体同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 161.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 08:57:30 | ||
图片预览

文档简介
1.1.1认识几何体同步练习题
2021-2022学年北师大版七年级数学上册第一章
A组(基础题)
一、填空题
1.写出下列物体类似的几何图形:
数学课本:________;笔筒:________;金字塔:________;西瓜:________.
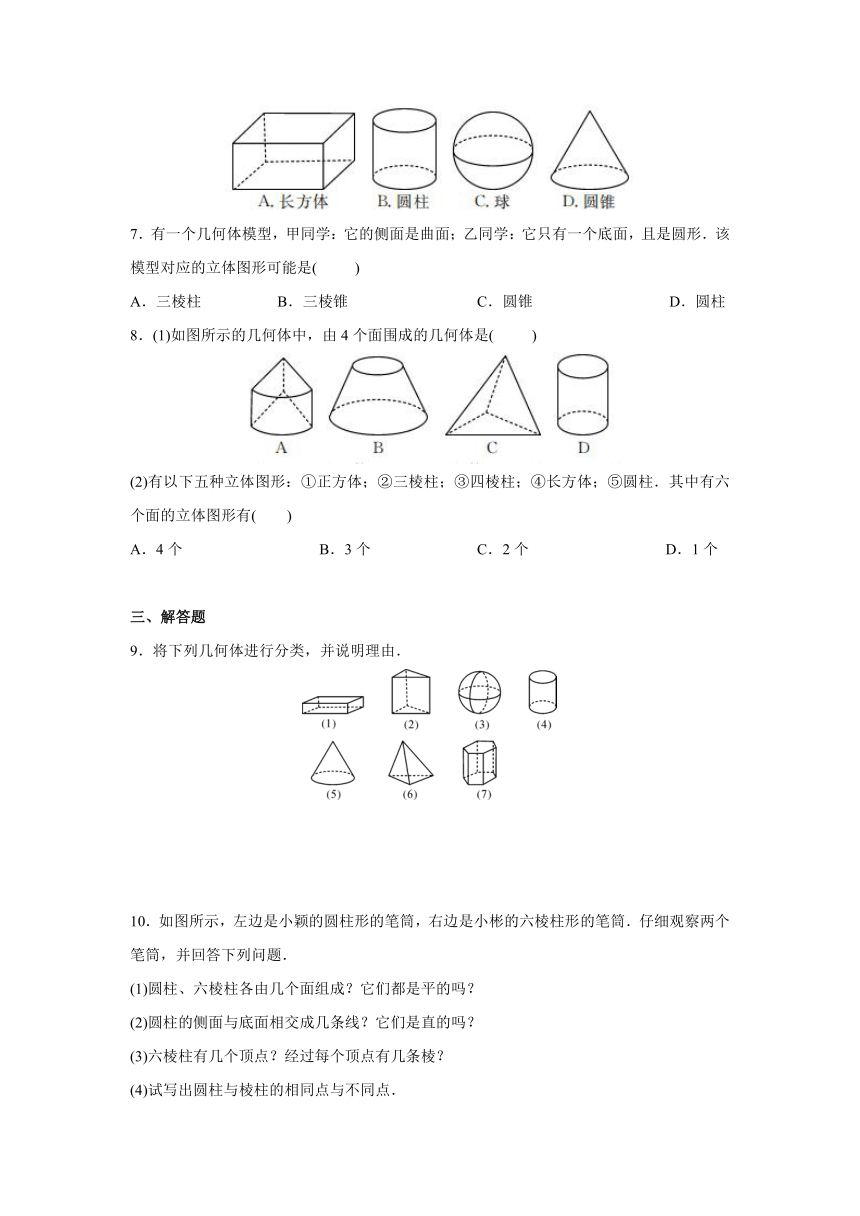
2.请将下列几何体分类.
(1)如果按“柱”“锥”“球”来分,柱体有________,锥体有________,球有________;
(2)如果按“有无曲面”来分,有曲面的有________,无曲面的有________;
(3)如果按“有无顶点”来分,有顶点的有________,无顶点的有________.
3.(1)如图,斜四棱柱中,一共有________条棱.
(2)一个六棱柱有________条棱,________个面.
4.一个棱柱有16个顶点,所有侧棱长的和是64
cm,则每条侧棱的长是________.
二、选择题
5.下列几何体中,是圆锥的为(
)
6.围成下列立体图形的各个面中,每个面都是平面的是(
)
7.有一个几何体模型,甲同学:它的侧面是曲面;乙同学:它只有一个底面,且是圆形.该模型对应的立体图形可能是(
)
A.三棱柱
B.三棱锥
C.圆锥
D.圆柱
8.(1)如图所示的几何体中,由4个面围成的几何体是(
)
(2)有以下五种立体图形:①正方体;②三棱柱;③四棱柱;④长方体;⑤圆柱.其中有六个面的立体图形有(
)
A.4个
B.3个
C.2个
D.1个
三、解答题
9.将下列几何体进行分类,并说明理由.
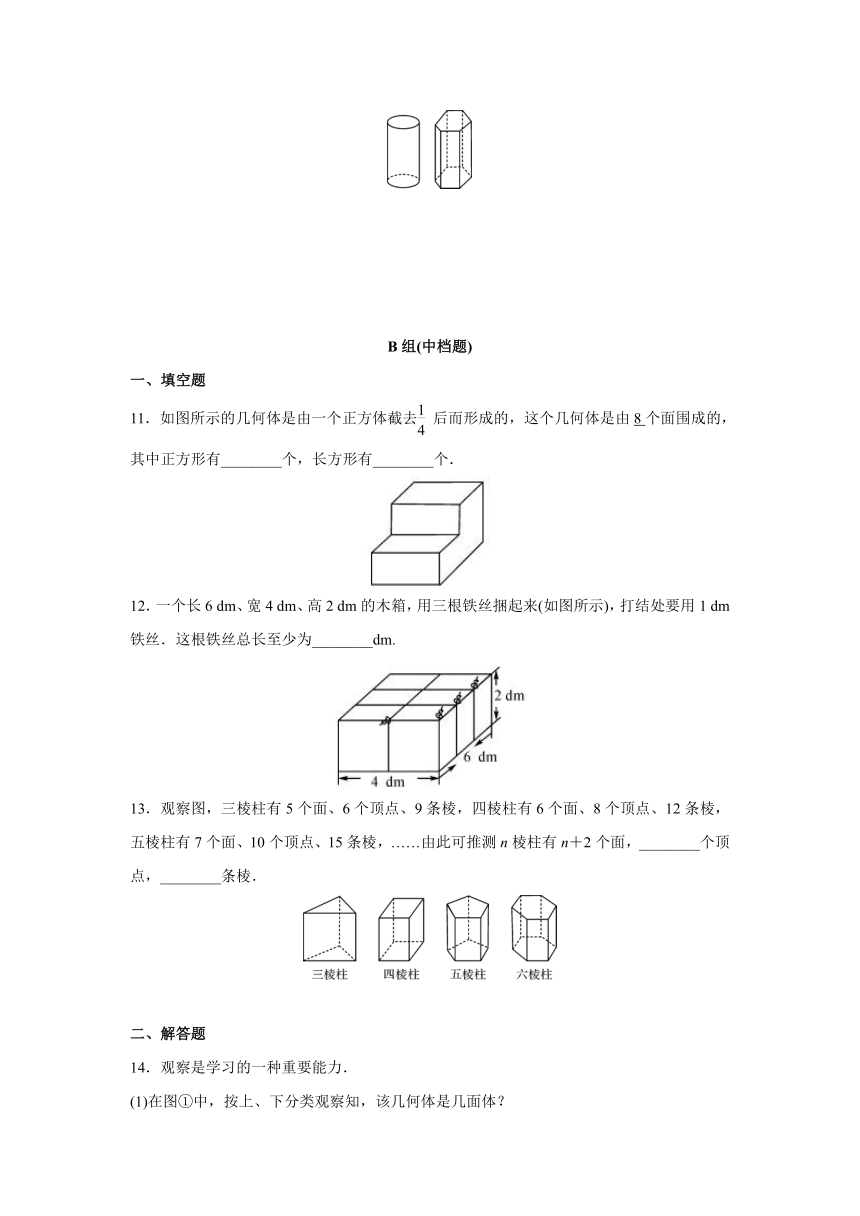
10.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下列问题.
(1)圆柱、六棱柱各由几个面组成?它们都是平的吗?
(2)圆柱的侧面与底面相交成几条线?它们是直的吗?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点.
B组(中档题)
一、填空题
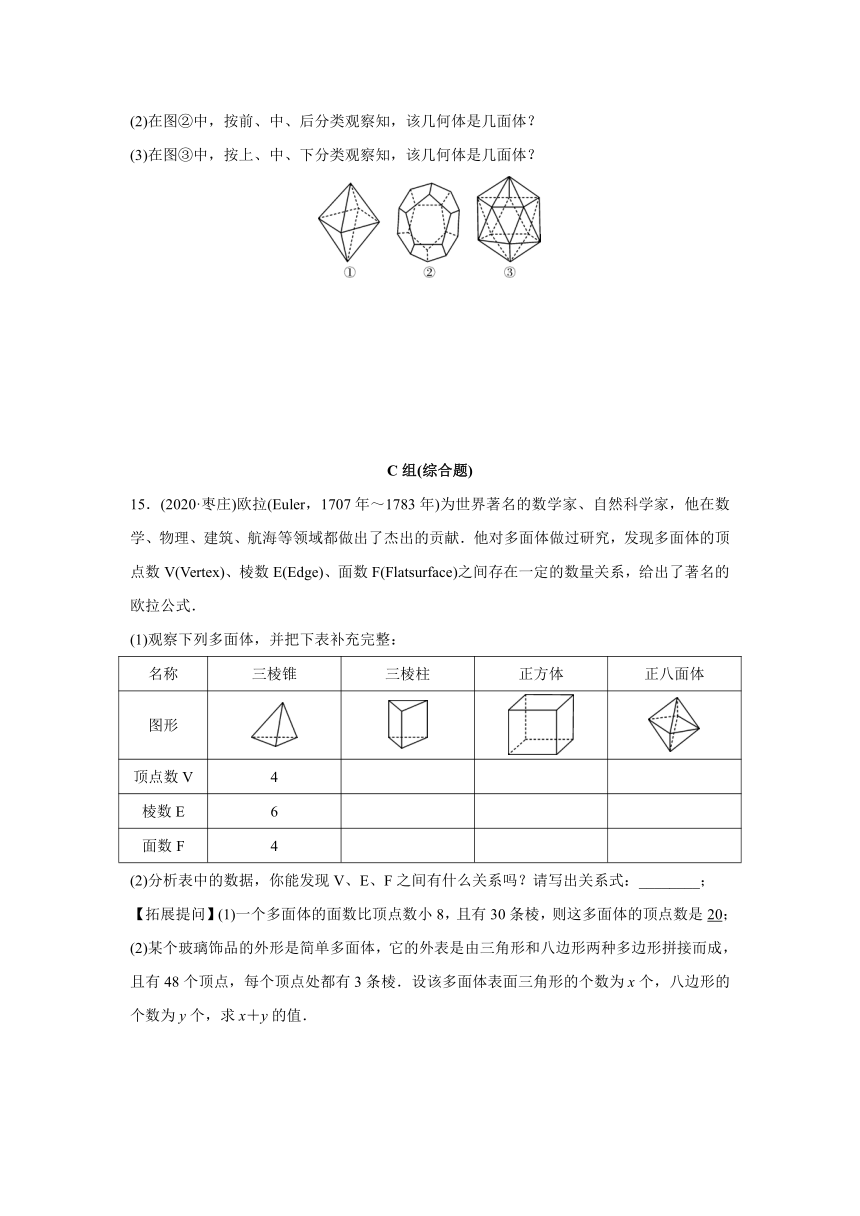
11.如图所示的几何体是由一个正方体截去后而形成的,这个几何体是由8个面围成的,其中正方形有________个,长方形有________个.
12.一个长6
dm、宽4
dm、高2
dm的木箱,用三根铁丝捆起来(如图所示),打结处要用1
dm铁丝.这根铁丝总长至少为________dm.
13.观察图,三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,……由此可推测n棱柱有n+2个面,________个顶点,________条棱.
二、解答题
14.观察是学习的一种重要能力.
(1)在图①中,按上、下分类观察知,该几何体是几面体?
(2)在图②中,按前、中、后分类观察知,该几何体是几面体?
(3)在图③中,按上、中、下分类观察知,该几何体是几面体?
C组(综合题)
15.(2020·枣庄)欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数V(Vertex)、棱数E(Edge)、面数F(Flatsurface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称
三棱锥
三棱柱
正方体
正八面体
图形
顶点数V
4
棱数E
6
面数F
4
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:________;
【拓展提问】(1)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是20;
(2)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱.设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
参考答案
1.1.1认识几何体同步练习题
2021-2022学年北师大版七年级数学上册第一章
A组(基础题)
一、填空题
1.写出下列物体类似的几何图形:
数学课本:长方体;笔筒:圆柱;金字塔:四棱锥;西瓜:球.
2.请将下列几何体分类.
(1)如果按“柱”“锥”“球”来分,柱体有①②③⑥⑧,锥体有④⑦,球有⑤;
(2)如果按“有无曲面”来分,有曲面的有③④⑤,无曲面的有①②⑥⑦⑧;
(3)如果按“有无顶点”来分,有顶点的有①②④⑥⑦⑧,无顶点的有③⑤.
3.(1)如图,斜四棱柱中,一共有12条棱.
(2)一个六棱柱有18条棱,8个面.
4.一个棱柱有16个顶点,所有侧棱长的和是64
cm,则每条侧棱的长是8__cm.
二、选择题
5.下列几何体中,是圆锥的为(
C
)
6.围成下列立体图形的各个面中,每个面都是平面的是(
A
)
7.有一个几何体模型,甲同学:它的侧面是曲面;乙同学:它只有一个底面,且是圆形.该模型对应的立体图形可能是(
C
)
A.三棱柱
B.三棱锥
C.圆锥
D.圆柱
8.(1)如图所示的几何体中,由4个面围成的几何体是(
C
)
(2)有以下五种立体图形:①正方体;②三棱柱;③四棱柱;④长方体;⑤圆柱.其中有六个面的立体图形有(
B
)
A.4个
B.3个
C.2个
D.1个
三、解答题
9.将下列几何体进行分类,并说明理由.
解:分类首先要确定标准,可以按组成几何体的面的平或曲来划分,也可以按柱、锥、球来划分.
(1)长方体是由平面组成的,属于柱体.
(2)三棱柱是由平面组成的,属于柱体.
(3)球体是由曲面组成的,属于球体.
(4)圆柱是由平面和曲面组成的,属于柱体.
(5)圆锥是由曲面与平面组成的,属于锥体.
(6)四棱锥是由平面组成的,属于锥体.
(7)六棱柱是由平面组成的,属于柱体.
若按组成几何体的面的平或曲来划分:(1)(2)(6)(7)是一类,组成它的面都是平面;(3)(4)(5)是一类,组成它的面至少有一个是曲面.
若按柱、锥、球来划分:(1)(2)(4)(7)是一类,即柱体;(5)(6)是一类,即锥体;(3)是球体.
10.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下列问题.
(1)圆柱、六棱柱各由几个面组成?它们都是平的吗?
(2)圆柱的侧面与底面相交成几条线?它们是直的吗?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点.
解:(1)圆柱有3个面,六棱柱有8个面,圆柱有两个平面,有一个曲面,棱柱的8个面都是平面.
(2)圆柱的侧面与底面相交形成1条线,是一条曲线.
(3)六棱柱共有12个顶点,经过每个顶点有3条棱.
(4)棱柱与圆柱的相同点:都是柱体;
棱柱与圆柱的不同点:棱柱与圆柱的底面形状不同,棱柱的底面是多边形,圆柱的底面是圆形,圆柱的侧面是曲面,而棱柱的侧面是长方形.
B组(中档题)
一、填空题
11.如图所示的几何体是由一个正方体截去后而形成的,这个几何体是由8个面围成的,其中正方形有2个,长方形有4个.
12.一个长6
dm、宽4
dm、高2
dm的木箱,用三根铁丝捆起来(如图所示),打结处要用1
dm铁丝.这根铁丝总长至少为43dm.
13.观察图,三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,……由此可推测n棱柱有n+2个面,2n个顶点,3n条棱.
二、解答题
14.观察是学习的一种重要能力.
(1)在图①中,按上、下分类观察知,该几何体是几面体?
(2)在图②中,按前、中、后分类观察知,该几何体是几面体?
(3)在图③中,按上、中、下分类观察知,该几何体是几面体?
解:(1)在图①中,按上、下分类观察知,该几何体是8面体.
(2)在图②中,按前、中、后分类观察知,该几何体是12面体.
(3)在图③中,按上、中、下分类观察知,该几何体是20面体.
C组(综合题)
15.(2020·枣庄)欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数V(Vertex)、棱数E(Edge)、面数F(Flatsurface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称
三棱锥
三棱柱
正方体
正八面体
图形
顶点数V
4
6
8
6
棱数E
6
9
12
12
面数F
4
5
6
8
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:V+F-E=2;
【拓展提问】(1)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是20;
(2)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱.设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
解:因为有48个顶点,每个顶点处都有3条棱,
所以共有48×3÷2=72(条).
设总面数为F,
则48+F-72=2,解得F=26.
所以x+y=26.
2021-2022学年北师大版七年级数学上册第一章
A组(基础题)
一、填空题
1.写出下列物体类似的几何图形:
数学课本:________;笔筒:________;金字塔:________;西瓜:________.
2.请将下列几何体分类.
(1)如果按“柱”“锥”“球”来分,柱体有________,锥体有________,球有________;
(2)如果按“有无曲面”来分,有曲面的有________,无曲面的有________;
(3)如果按“有无顶点”来分,有顶点的有________,无顶点的有________.
3.(1)如图,斜四棱柱中,一共有________条棱.
(2)一个六棱柱有________条棱,________个面.
4.一个棱柱有16个顶点,所有侧棱长的和是64
cm,则每条侧棱的长是________.
二、选择题
5.下列几何体中,是圆锥的为(
)
6.围成下列立体图形的各个面中,每个面都是平面的是(
)
7.有一个几何体模型,甲同学:它的侧面是曲面;乙同学:它只有一个底面,且是圆形.该模型对应的立体图形可能是(
)
A.三棱柱
B.三棱锥
C.圆锥
D.圆柱
8.(1)如图所示的几何体中,由4个面围成的几何体是(
)
(2)有以下五种立体图形:①正方体;②三棱柱;③四棱柱;④长方体;⑤圆柱.其中有六个面的立体图形有(
)
A.4个
B.3个
C.2个
D.1个
三、解答题
9.将下列几何体进行分类,并说明理由.
10.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下列问题.
(1)圆柱、六棱柱各由几个面组成?它们都是平的吗?
(2)圆柱的侧面与底面相交成几条线?它们是直的吗?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点.
B组(中档题)
一、填空题
11.如图所示的几何体是由一个正方体截去后而形成的,这个几何体是由8个面围成的,其中正方形有________个,长方形有________个.
12.一个长6
dm、宽4
dm、高2
dm的木箱,用三根铁丝捆起来(如图所示),打结处要用1
dm铁丝.这根铁丝总长至少为________dm.
13.观察图,三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,……由此可推测n棱柱有n+2个面,________个顶点,________条棱.
二、解答题
14.观察是学习的一种重要能力.
(1)在图①中,按上、下分类观察知,该几何体是几面体?
(2)在图②中,按前、中、后分类观察知,该几何体是几面体?
(3)在图③中,按上、中、下分类观察知,该几何体是几面体?
C组(综合题)
15.(2020·枣庄)欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数V(Vertex)、棱数E(Edge)、面数F(Flatsurface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称
三棱锥
三棱柱
正方体
正八面体
图形
顶点数V
4
棱数E
6
面数F
4
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:________;
【拓展提问】(1)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是20;
(2)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱.设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
参考答案
1.1.1认识几何体同步练习题
2021-2022学年北师大版七年级数学上册第一章
A组(基础题)
一、填空题
1.写出下列物体类似的几何图形:
数学课本:长方体;笔筒:圆柱;金字塔:四棱锥;西瓜:球.
2.请将下列几何体分类.
(1)如果按“柱”“锥”“球”来分,柱体有①②③⑥⑧,锥体有④⑦,球有⑤;
(2)如果按“有无曲面”来分,有曲面的有③④⑤,无曲面的有①②⑥⑦⑧;
(3)如果按“有无顶点”来分,有顶点的有①②④⑥⑦⑧,无顶点的有③⑤.
3.(1)如图,斜四棱柱中,一共有12条棱.
(2)一个六棱柱有18条棱,8个面.
4.一个棱柱有16个顶点,所有侧棱长的和是64
cm,则每条侧棱的长是8__cm.
二、选择题
5.下列几何体中,是圆锥的为(
C
)
6.围成下列立体图形的各个面中,每个面都是平面的是(
A
)
7.有一个几何体模型,甲同学:它的侧面是曲面;乙同学:它只有一个底面,且是圆形.该模型对应的立体图形可能是(
C
)
A.三棱柱
B.三棱锥
C.圆锥
D.圆柱
8.(1)如图所示的几何体中,由4个面围成的几何体是(
C
)
(2)有以下五种立体图形:①正方体;②三棱柱;③四棱柱;④长方体;⑤圆柱.其中有六个面的立体图形有(
B
)
A.4个
B.3个
C.2个
D.1个
三、解答题
9.将下列几何体进行分类,并说明理由.
解:分类首先要确定标准,可以按组成几何体的面的平或曲来划分,也可以按柱、锥、球来划分.
(1)长方体是由平面组成的,属于柱体.
(2)三棱柱是由平面组成的,属于柱体.
(3)球体是由曲面组成的,属于球体.
(4)圆柱是由平面和曲面组成的,属于柱体.
(5)圆锥是由曲面与平面组成的,属于锥体.
(6)四棱锥是由平面组成的,属于锥体.
(7)六棱柱是由平面组成的,属于柱体.
若按组成几何体的面的平或曲来划分:(1)(2)(6)(7)是一类,组成它的面都是平面;(3)(4)(5)是一类,组成它的面至少有一个是曲面.
若按柱、锥、球来划分:(1)(2)(4)(7)是一类,即柱体;(5)(6)是一类,即锥体;(3)是球体.
10.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下列问题.
(1)圆柱、六棱柱各由几个面组成?它们都是平的吗?
(2)圆柱的侧面与底面相交成几条线?它们是直的吗?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点.
解:(1)圆柱有3个面,六棱柱有8个面,圆柱有两个平面,有一个曲面,棱柱的8个面都是平面.
(2)圆柱的侧面与底面相交形成1条线,是一条曲线.
(3)六棱柱共有12个顶点,经过每个顶点有3条棱.
(4)棱柱与圆柱的相同点:都是柱体;
棱柱与圆柱的不同点:棱柱与圆柱的底面形状不同,棱柱的底面是多边形,圆柱的底面是圆形,圆柱的侧面是曲面,而棱柱的侧面是长方形.
B组(中档题)
一、填空题
11.如图所示的几何体是由一个正方体截去后而形成的,这个几何体是由8个面围成的,其中正方形有2个,长方形有4个.
12.一个长6
dm、宽4
dm、高2
dm的木箱,用三根铁丝捆起来(如图所示),打结处要用1
dm铁丝.这根铁丝总长至少为43dm.
13.观察图,三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,……由此可推测n棱柱有n+2个面,2n个顶点,3n条棱.
二、解答题
14.观察是学习的一种重要能力.
(1)在图①中,按上、下分类观察知,该几何体是几面体?
(2)在图②中,按前、中、后分类观察知,该几何体是几面体?
(3)在图③中,按上、中、下分类观察知,该几何体是几面体?
解:(1)在图①中,按上、下分类观察知,该几何体是8面体.
(2)在图②中,按前、中、后分类观察知,该几何体是12面体.
(3)在图③中,按上、中、下分类观察知,该几何体是20面体.
C组(综合题)
15.(2020·枣庄)欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数V(Vertex)、棱数E(Edge)、面数F(Flatsurface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称
三棱锥
三棱柱
正方体
正八面体
图形
顶点数V
4
6
8
6
棱数E
6
9
12
12
面数F
4
5
6
8
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:V+F-E=2;
【拓展提问】(1)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是20;
(2)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱.设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
解:因为有48个顶点,每个顶点处都有3条棱,
所以共有48×3÷2=72(条).
设总面数为F,
则48+F-72=2,解得F=26.
所以x+y=26.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
