2.6 应用一元二次方程习题精练- 2021-2022学年北师大版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 2.6 应用一元二次方程习题精练- 2021-2022学年北师大版数学九年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 45.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 09:59:37 | ||
图片预览


文档简介
北师大版九年级第二章6应用一元二次方程习题精练
一、选择题
在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡42张,则参加活动的同学有
A.
6人
B.
7人
C.
8人
D.
9人
某城市2006年底已有绿化面积300公顷,经过两年的绿化,绿化面积逐年增加,如果设绿化面积平均每年的增长率为x,关于代数式下列说法正确的是
A.
2007年已有的绿化面积
B.
2008年增加的绿化面积
C.
2008年已有的绿化面积
D.
2007、2008年共增加的绿化面积
为提高人民生活幸福指数,某药厂决定降低药品的价格,已知某药品2019年的售价是100元,2021年的售价是81元,若年平均降价率相同,则年平均降价率是?
?
A.
B.
C.
D.
甲、乙两人同驾一辆车出游,各匀速驾驶一半路程,共用3小时,到达目的地后,甲对乙说:“我用你所花的时间,可以行驶180km”乙对甲说:“我用你所花的时间,只能行驶80km”从他们的交谈中可以判断,乙驾车的时长为?
?
A.
小时
B.
小时
C.
小时
D.
2小时
有一人患流感,经过两轮传染后,共有49人患了流感.如果不及时控制,第三轮被传染的人数为
A.
234人
B.
264人
C.
284人
D.
294人
在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为
A.
9
B.
10
C.
11
D.
12
毕业之际,某校九年级数学兴趣小组的同学相约到同一家礼品店购买纪念品,每两个同学都相互赠送一件礼品,礼品店共售出礼品30件,则该兴趣小组的人数为
A.
5人
B.
6人
C.
7人
D.
8人
组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛设比赛组织者应邀请x个队参赛,则x满足的关系式为?
?
A.
B.
C.
D.
某商品原价200元,连续两次降价后售价为148元,下列所列方程正确的是
A.
B.
C.
D.
如图1,有一张长80cm,宽50cm的长方形硬纸片,裁去角上四个小正方形之后,折成如图2那样的无盖纸盒,若纸盘的底面积是,设纸盒的高为,那么x满足的方程是
A.
B.
C.
D.
二、填空题
两年前生产1吨甲种药品的成本是元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,则甲药品成本的年平均下降率??????????乙药品成本的年平均下降率填“大于”“小于”或“等于”
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出据市场调查:每个玩具按480元销售时,每天可销售160个若销售单价每降低1元,每天可多售出2个已知每个玩具的固定成本为360元若该厂家每天想要获利20000元,则这种玩具的销售单价为??????????元
若两个相邻偶数的积是168,则这两个偶数的和是??????????.
小欣去年开了一家商店,将每个月的盈亏情况都作了记录,今年1月份开始盈利,2月份盈利2000元,4月份盈利恰好为2880元若每月盈利的平均增长率为x,则列出的方程为___________________.
三、解答题
参加一次商品交易会的每两家公司之间都签订了一式三份合同两家公司各执一份,给公证处一份,所有公司共签订了84份合同则共有多少家公司参加了此次商品交易会
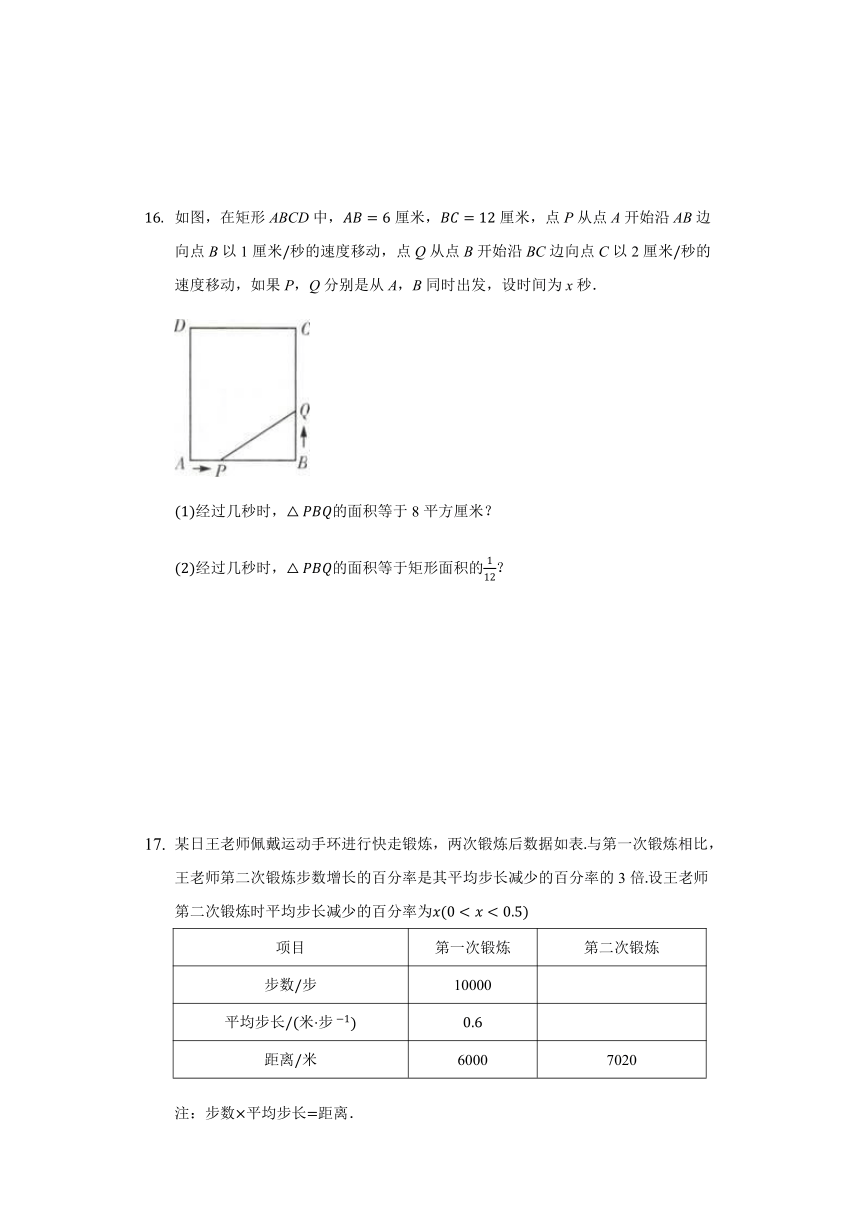
如图,在矩形ABCD中,厘米,厘米,点P从点A开始沿AB边向点B以1厘米秒的速度移动,点Q从点B开始沿BC边向点C以2厘米秒的速度移动,如果P,Q分别是从A,B同时出发,设时间为x秒.
经过几秒时,的面积等于8平方厘米?
经过几秒时,的面积等于矩形面积的?
某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍设王老师第二次锻炼时平均步长减少的百分率为
项目
第一次锻炼
第二次锻炼
步数步
10000
平均步长米步
距离米
6000
7020
注:步数平均步长距离.
根据题意完成表格填空.
求x的值.
王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
某生物实验室需培育一群有益菌现有60个活体样本,经过两轮培植后,有益菌总和达24000个,其中每个有益菌每一轮可分裂出若干个相同数目的有益菌.
每轮分裂中每个有益菌可分裂出多少个有益菌
按照这样的分裂速度,经过三轮培植后共有多少个有益菌
答案和解析
1.【答案】B
【解析】解:设参加此次活动的人数有x人,
由题意得:,
解得:,不合题意,舍去.
即参加此次活动的人数是7人.
故选B.
2.【答案】C
【解析】解:2006年底已有绿化面积300公顷,经过两年的绿化,绿化面积逐年增加,如果设绿化面积平均每年的增长率为x,代数式表示增长两年后的绿化面积,即:2008年已有的绿化面积,
故选:C.??
3.【答案】A
【解析】略
4.【答案】C
【解析】略
5.【答案】D
【解析】
解:设一个患者一次传染给x人,
由题意,得,
解得:,舍去,
一个患者一次传染给6个人,
第三轮被传染的人数是:人.
故选D.??
6.【答案】C
【解析】
解:设参加酒会的人数为x,
根据题意得,
整理得,
解得,不合题意,舍去.
故选C.??
7.【答案】B
【解析】
解:设该兴趣小组的人数为x人.
,
解得,不合题意,舍去,
故选:B.??
8.【答案】B
【解析】略
9.【答案】B
【解析】
解:依题意得两次降价后的售价为,
.
故选:B.??
10.【答案】D
【解析】解:设纸盒的高是x,根据题意得:.
故选:D.
设纸盒的高是x,根据长方形的面积公式列出算式,再进行求解即可.
此题考查了由实际问题抽象出一元二次方程,掌握长方形的面积计算公式是解决问题的关键.
11.【答案】等于
【解析】略
12.【答案】460【解析】略
13.【答案】【解析】略
14.【答案】
【解析】解:设每月盈利的平均增长率为x,根据题意得:
.
故答案为.??
15.【答案】解:设共有x家公司参加了此次商品交易会,
则由题意可得,
解得,不合题意,舍去.
答:共有8家公司参加了此次商品交易会.
16.【答案】解:厘米,厘米.
根据题意,得,
整理,得,
解得,.
故经过2秒或4秒时,的面积等于8平方厘米.
厘米,厘米,
根据题意,得,
整理,得,
解得,.
故经过秒或秒时,的面积等于矩形面积的.
【解析】此题考查了一元二次方程的应用,用到的知识点是三角形、矩形的面积公式,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
根据厘米,厘米,点P从点A开始沿AB边向点B以1厘米秒的速度移动,点Q从点B开始沿BC边向点C以2厘米秒的速度移动,得出厘米,厘米,再根据三角形的面积公式列方程求解即可;
根据三角形的面积公式和矩形的面积公式列出方程,然后求解即可.
17.【答案】解:?;;
的值为;
王老师这500米的平均步长为米.
18.【答案】设每轮分裂中每个有益菌可分裂出x个有益菌,根据题意,得
.
解得,不合题意,舍去.
答:每轮分裂中每个有益菌可分裂出19个有益菌.
个.
答:经过三轮培植后共有480000个有益菌.
第2页,共2页
一、选择题
在元旦庆祝活动中,参加活动的同学互赠贺卡,共送贺卡42张,则参加活动的同学有
A.
6人
B.
7人
C.
8人
D.
9人
某城市2006年底已有绿化面积300公顷,经过两年的绿化,绿化面积逐年增加,如果设绿化面积平均每年的增长率为x,关于代数式下列说法正确的是
A.
2007年已有的绿化面积
B.
2008年增加的绿化面积
C.
2008年已有的绿化面积
D.
2007、2008年共增加的绿化面积
为提高人民生活幸福指数,某药厂决定降低药品的价格,已知某药品2019年的售价是100元,2021年的售价是81元,若年平均降价率相同,则年平均降价率是?
?
A.
B.
C.
D.
甲、乙两人同驾一辆车出游,各匀速驾驶一半路程,共用3小时,到达目的地后,甲对乙说:“我用你所花的时间,可以行驶180km”乙对甲说:“我用你所花的时间,只能行驶80km”从他们的交谈中可以判断,乙驾车的时长为?
?
A.
小时
B.
小时
C.
小时
D.
2小时
有一人患流感,经过两轮传染后,共有49人患了流感.如果不及时控制,第三轮被传染的人数为
A.
234人
B.
264人
C.
284人
D.
294人
在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为
A.
9
B.
10
C.
11
D.
12
毕业之际,某校九年级数学兴趣小组的同学相约到同一家礼品店购买纪念品,每两个同学都相互赠送一件礼品,礼品店共售出礼品30件,则该兴趣小组的人数为
A.
5人
B.
6人
C.
7人
D.
8人
组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛设比赛组织者应邀请x个队参赛,则x满足的关系式为?
?
A.
B.
C.
D.
某商品原价200元,连续两次降价后售价为148元,下列所列方程正确的是
A.
B.
C.
D.
如图1,有一张长80cm,宽50cm的长方形硬纸片,裁去角上四个小正方形之后,折成如图2那样的无盖纸盒,若纸盘的底面积是,设纸盒的高为,那么x满足的方程是
A.
B.
C.
D.
二、填空题
两年前生产1吨甲种药品的成本是元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,则甲药品成本的年平均下降率??????????乙药品成本的年平均下降率填“大于”“小于”或“等于”
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出据市场调查:每个玩具按480元销售时,每天可销售160个若销售单价每降低1元,每天可多售出2个已知每个玩具的固定成本为360元若该厂家每天想要获利20000元,则这种玩具的销售单价为??????????元
若两个相邻偶数的积是168,则这两个偶数的和是??????????.
小欣去年开了一家商店,将每个月的盈亏情况都作了记录,今年1月份开始盈利,2月份盈利2000元,4月份盈利恰好为2880元若每月盈利的平均增长率为x,则列出的方程为___________________.
三、解答题
参加一次商品交易会的每两家公司之间都签订了一式三份合同两家公司各执一份,给公证处一份,所有公司共签订了84份合同则共有多少家公司参加了此次商品交易会
如图,在矩形ABCD中,厘米,厘米,点P从点A开始沿AB边向点B以1厘米秒的速度移动,点Q从点B开始沿BC边向点C以2厘米秒的速度移动,如果P,Q分别是从A,B同时出发,设时间为x秒.
经过几秒时,的面积等于8平方厘米?
经过几秒时,的面积等于矩形面积的?
某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍设王老师第二次锻炼时平均步长减少的百分率为
项目
第一次锻炼
第二次锻炼
步数步
10000
平均步长米步
距离米
6000
7020
注:步数平均步长距离.
根据题意完成表格填空.
求x的值.
王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
某生物实验室需培育一群有益菌现有60个活体样本,经过两轮培植后,有益菌总和达24000个,其中每个有益菌每一轮可分裂出若干个相同数目的有益菌.
每轮分裂中每个有益菌可分裂出多少个有益菌
按照这样的分裂速度,经过三轮培植后共有多少个有益菌
答案和解析
1.【答案】B
【解析】解:设参加此次活动的人数有x人,
由题意得:,
解得:,不合题意,舍去.
即参加此次活动的人数是7人.
故选B.
2.【答案】C
【解析】解:2006年底已有绿化面积300公顷,经过两年的绿化,绿化面积逐年增加,如果设绿化面积平均每年的增长率为x,代数式表示增长两年后的绿化面积,即:2008年已有的绿化面积,
故选:C.??
3.【答案】A
【解析】略
4.【答案】C
【解析】略
5.【答案】D
【解析】
解:设一个患者一次传染给x人,
由题意,得,
解得:,舍去,
一个患者一次传染给6个人,
第三轮被传染的人数是:人.
故选D.??
6.【答案】C
【解析】
解:设参加酒会的人数为x,
根据题意得,
整理得,
解得,不合题意,舍去.
故选C.??
7.【答案】B
【解析】
解:设该兴趣小组的人数为x人.
,
解得,不合题意,舍去,
故选:B.??
8.【答案】B
【解析】略
9.【答案】B
【解析】
解:依题意得两次降价后的售价为,
.
故选:B.??
10.【答案】D
【解析】解:设纸盒的高是x,根据题意得:.
故选:D.
设纸盒的高是x,根据长方形的面积公式列出算式,再进行求解即可.
此题考查了由实际问题抽象出一元二次方程,掌握长方形的面积计算公式是解决问题的关键.
11.【答案】等于
【解析】略
12.【答案】460【解析】略
13.【答案】【解析】略
14.【答案】
【解析】解:设每月盈利的平均增长率为x,根据题意得:
.
故答案为.??
15.【答案】解:设共有x家公司参加了此次商品交易会,
则由题意可得,
解得,不合题意,舍去.
答:共有8家公司参加了此次商品交易会.
16.【答案】解:厘米,厘米.
根据题意,得,
整理,得,
解得,.
故经过2秒或4秒时,的面积等于8平方厘米.
厘米,厘米,
根据题意,得,
整理,得,
解得,.
故经过秒或秒时,的面积等于矩形面积的.
【解析】此题考查了一元二次方程的应用,用到的知识点是三角形、矩形的面积公式,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
根据厘米,厘米,点P从点A开始沿AB边向点B以1厘米秒的速度移动,点Q从点B开始沿BC边向点C以2厘米秒的速度移动,得出厘米,厘米,再根据三角形的面积公式列方程求解即可;
根据三角形的面积公式和矩形的面积公式列出方程,然后求解即可.
17.【答案】解:?;;
的值为;
王老师这500米的平均步长为米.
18.【答案】设每轮分裂中每个有益菌可分裂出x个有益菌,根据题意,得
.
解得,不合题意,舍去.
答:每轮分裂中每个有益菌可分裂出19个有益菌.
个.
答:经过三轮培植后共有480000个有益菌.
第2页,共2页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
