5.6应用一元一次方程 追赶小明 同步练习2021-2022学年北师大版数学七年级上册(Word版 含答案)
文档属性
| 名称 | 5.6应用一元一次方程 追赶小明 同步练习2021-2022学年北师大版数学七年级上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 00:00:00 | ||
图片预览




文档简介
应用一元一次方程——追赶小明
一、单选题
1.方方早上骑自行车上学,中途因道路施工推车步行了一段路,到学校共用时15分钟.如果他骑自行车的平均速度是每分钟250米,推车步行的平均速度是每分钟80米,他家离学校的路程是2900米,设他推车步行的时间为分钟,那么可列出的方程是(
)
A.
B.
C.
D.
2.小亮原计划骑车以10千米/时的速度由A地去B地,这样就可以在规定时间到达B地,但他因故比原计划晚出发15分钟,只好以15千米/时的速度前进,结果比规定时间早到6分钟,若设A,B两地间的距离为x千米,则根据题意列出的方程正确的为(
)
A.+15+6
B.
C.
D.
3.甲、乙两人分别从两地同时骑自行车相向而行,2小时后在途中相遇,相遇后,甲、乙骑自行车的速度都提高了1千米/小时,当甲到达地后立刻以原路和提高后的速度向地返行,乙到达地后也立刻以原路和提高后的速度向地返行.甲、乙两人在开始
出发后的5小时36分钟又再次相遇,则两地的距离是(
)
A.24千米
B.30千米
C.32千米
D.36千米
4.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是(
)
A.
B.
C.
D.
5.一辆汽车从甲地行驶到乙地,第一小时行驶了全程的,第二小时行驶了全程的,此时离乙地还有150千米的路程,设甲、乙两地间的距离为千米,则下列方程正确的是(
)
A.
B.
C.
D.
6.我国元朝的数学著作《算学启蒙》记载:良马日行二百四十里,驽马日行一百五十里,两马同地出发,驽马先行一十二日,问良马几何追及之?其大意是:良马每天跑里,驽马每天跑里.
良马和驽马从同地出发,驽马先走天,问良马追上驽马的时间为多少天?若设良马追上驽马的时间为天,则可列方程为(
)
A.
B.
C.
D.
7.某铁路桥长1200m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.则火车的长度为(
)
A.180m
B.200m
C.240m
D.250m
8.小明从家里骑自行车到学校,每小时骑,可早到10分钟,每小时骑就会迟到5分钟.他家到学校的路程是多少?设他家到学校的路程是,则据题意列出的方程是(
)
A.
B.
C.
D.
9.甲、乙两人从同一地点出发,如果甲先出发2小时后,乙从后面追赶,那么当乙追上甲时,下面说法正确的是(
)
A.乙比甲多走了2小时
B.乙走的路程比甲多
C.甲、乙所用的时间相等
D.甲、乙所走的路程相等
10.甲、乙两人在长为25米泳池内始终以匀速游泳,两人同时从起点出发,触壁后原路返回,如是往返;甲的速度是1米/秒,乙的速度是0.6米/秒,那么第十次迎面相遇时他们离起点(
)
A.7.5米
B.10米
C.12米
D.12.5米
11.甲、乙两名运动员在圆形跑道上从点同时出发,并按相反方向匀速跑步,甲的速度为每秒6米,乙的速度为每秒7米,当他们第一次在点再度相遇时跑步就结束.则从他们开始出发(算第一次相遇)到结束(算最后一次相遇)共相遇次数是(
)
A.13
B.14
C.42
D.43
12.小明和小亮进行100米赛跑,两人在同一起跑线上,结果第一次比赛时小明胜10米;在进行第二次比赛时,小明的起跑线比原来起跑线推后10米,如果两次他们速度不变,则第二次结果(
)胜.
A.小亮胜
B.小明胜
C.同时到达
D.不能确定
二、填空题
13.一条船顺流航行,每小时行驶20千米;逆流航行,每小时行驶16千米若水的流速与船在静水中的速度都是不变的,则轮船在静水中的速度为______________千米/小时.
14.一人步行从甲地去乙地,第一天行若干千米,自第二天起,每一天都比前一天多走同样的路程,这样10天可以到达乙地;如果每天都以第一天所行的相同路程步行,用15天才能到达乙地;如果每天都以第一种走法的最后一天所行的路程步行到乙地,需要______天.
15.小华和小明周末到北京三山五园绿道骑行.他们按设计好的同一条线路同时出发,小华每小时骑行,小明每小时骑行,他们完成全部行程所用的时间,小明比小华多半小时.设他们这次骑行线路长为,依题意,可列方程为__________.
16.甲、乙二人赛跑,每秒钟甲比乙所跑的路程多,现在甲在乙后面24米所处同时启程,15秒钟后,甲已到终点,乙落后甲6米,则甲跑过的距离为______.
17.一列慢车和一列快车都从站出发到站,它们的速度分别是60千米/时.100千米/时,慢车早发车半小时,结果快车到达站时,慢车刚到达离站50千米的站(站在.两站之间),则A.两站之间的距离是_____千米.
三、解答题
18.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”其意思为:速度快的人走100步,速度慢的人只走60步;现速度慢的人先走100步,速度快的人去追赶.问:速度快的人要走多少步才能追到速度慢的人?
19.甲、乙两列火车从A、B两地相向而行,乙车比甲车早发车,甲车比乙车速度每小时快,甲车发车两小时恰好与乙车相遇,相遇后为了错车,甲车放慢了速度,以它原来的速度行驶;而乙车加快了速度,以它原来的倍飞速行驶,结果后,两车距离又等于A、B两地之间的距离,求两车相遇前速度及A、B两地之间的距离.
20.在数轴上,点A、B分别对应实数和25,点M从A点出发,以每秒5个单位长度的速度沿数轴向右匀速运动;点N从A点以每秒7个单位长度的速度向右匀速运动;M,N两点到达B点后均停止运动;若点M出发1秒后点N才出发.
(1)点N出发后需要多长时间才追上点M?
(2)从点M出发开始到点M停止运动期间,何时M、N两点之间的距离刚好为1个单位长度?
21.在风速为的条件下,一架飞机顺风从机场飞到机场要用,它逆风飞行同样的航线要用.求:
(1)无风时这架飞机在这一航线的平均航速;
(2)两机场之间的航程.
22.据国际田联《田径场地设施标准手册》,400米标准跑道由两个平行的直道和两个半径相等的弯道组成,有8条跑道,每条跑道宽1.2米,直道长87米;跑道的弯道是半圆形,环形跑道第一圈(最内圈)弯道半径为35.00米到38.00米之间.
某校据国际田联标准和学校场地实际,建成第一圈弯道半径为36米的标准跑道.小王同学计算了各圈的长:
第一圈长:87×2+2π(36+1.2×0)≈400(米);
第二圈长:87×2+2π(36+1.2×1)≈408(米);
第三圈长:87×2+2π(36+1.2×2)≈415(米);
……
请问:
(1)第三圈半圆形弯道长比第一圈半圆形弯道长多多少米?小王计算的第八圈长是多少?
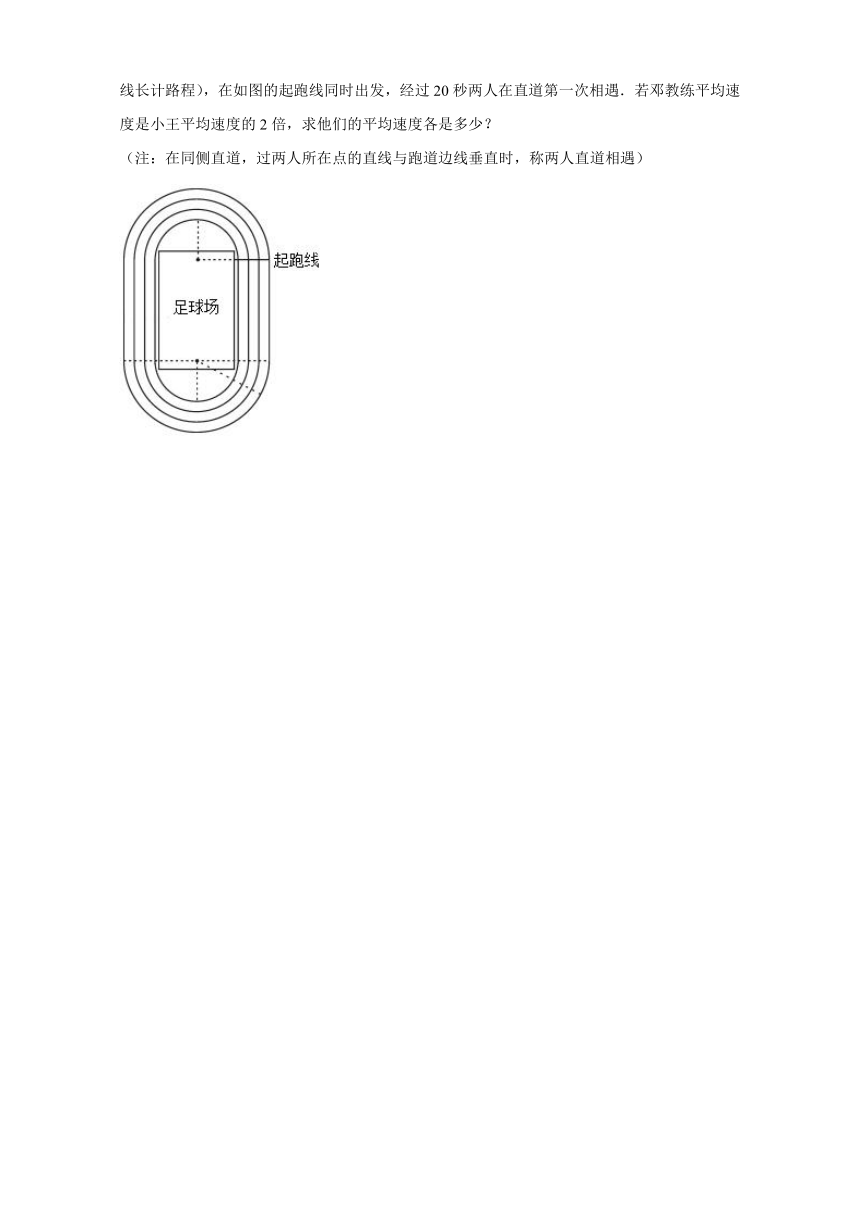
(2)小王紧靠第一圈边线逆时针跑步、邓教练紧靠第三圈边线顺时针骑自行车(均以所靠边线长计路程),在如图的起跑线同时出发,经过20秒两人在直道第一次相遇.若邓教练平均速度是小王平均速度的2倍,求他们的平均速度各是多少?
(注:在同侧直道,过两人所在点的直线与跑道边线垂直时,称两人直道相遇)
参考答案
1.A
解:设他推车步行的时间为分钟,骑自行车上学时间为(15-)分钟,
根据题意得:80x+250(15-)=2900,
变形得:250(15-x
)=2900-80x,.
故选择:A.
2.B
解:设A、B两地间的路程为x千米,
根据题意,得.
故选:B.
3.D
解:设第一次相遇时,甲、乙的速度和为xkm/h,
5小时36分钟=5(小时)
由题意可得:2×2x=(5-2)(x+2),
解得:x=18,
∴A、B两地的距离=2×18=36(km),
故选:D.
4.A
解:设A港和B港相距x千米,
根据题意得:.
故选:A.
5.C
解:由已知得:第一个小时行驶路程为,第二个小时行驶路程为,
故:,
整理得:.
故选:C.
6.B
解:设良马x天可以追上驽马,
依题意,得:240x=150(x+12).
故选:B.
7.C
解:设火车的长度为xm,
依题意,得:
,
解得:x=240.
故选:C.
8.A
解:设小明家到学校的路程是,根据题意列方程为:
故选A.
9.D
解:甲先出发2小时,甲多用时2小时。从同一地点出发,追到表示路程相等,
故选:D.
10.D
解:根据题意,画出图形可知:甲乙每迎面相遇一次,两人共行驶25×2=50米,
∴第十次迎面相遇时的总路程为50×10=500米
∴甲行驶的时间为500÷(1+)=s
∴甲行驶的路程为×1=米
∵一个来回共50米
∴÷50≈6个来回
∴此时距离出发点-50×6=米
故选D.
11.B
解:设路程为x,相向而行相遇时间=,相背而行相遇时间=,
根据题意可知最后相遇在A点时相遇次数=÷=13次,
则从他们开始出发(算第一次相遇)到结束(算最后一次相遇)共相遇次数=13+1=14次.
故选B.
12.B
解:设小明用的时间为t,则速度为v1=,
小亮的速度v2=,
第2次比赛时,s1′=100m+10m=110m,s2′=100m,
因为速度不变,所以小明用的时间:t1′=,
小亮用的时间:t2′=,
因为<t,即t1′<t2′,因此还是小明先到达终点,
故选:B.
13.18
解:设轮船在静水中的速度为千米小时,则水流速度为千米小时,
由题意可得:,
解得:,
轮船在静水中的速度为18千米小时,
故答案为:18.
14.7.5
解:设a是第一次第一天走的路程,b是第二天起每天多走的路程,x是所求的天数.则根据题意,得
15a=a+(a+b)+(a+2b)+(a+3b)+(a+4b)+(a+5b)+(a+6b)+(a+7b)+(a+8b)+(a+9b)=10a+45b,
∴15a=10a+45b,
∴5a=45b,
∴a=9b,
又∵15a=x(a+9b)
∴15a=x(a+a),解得
x=7.5
(天).
故答案为:7.5.
15.
解:设他们这次骑行线路长为,则小华完成全部行程的时间为小时,小明完成全部行程的时间为小时,
由题意得,
故答案为:.
16.180米
解:设乙的速度是v米/秒,则甲的速度是(1+)v米/秒,根据题意得:
(1+)v×15﹣15v=24+6,解得:v=10,
所以甲的速度是:10×(1+)=12(米/秒),
则甲跑的路程是:12×15=180米.
故答案为:180米.
17.200
解:设快车从A站出发x小时到达B站,则慢车出发了(x+0.5)小时,依题意列方程得:
60(x+0.5)+50=100x
解得:x=2
即快车从A站出发2小时到达B站,因此A、B两站之间的距离为100×2=200千米,
故答案为:200
18.250步
解:设速度快的人追到速度慢的人所用时间为t,
根据题意列方程得:100t=60t+100,
解得t=2.5,
2.5×100=250(步),
答:速度快的人要走250步才能追到速度慢的人.
19.相遇前甲车的速度为90km/h,乙车的速度为60km/h,A、B两地的距离为360km
解:设两车相遇前乙车的速度为xkm/h,则甲车的速度为km/h,
根据题意得:,
解得:,
,.
答:两车相遇前甲车的速度为90km/h,乙车的速度为60km/h,、两地的距离为360km.
20.(1)点N追上点M需要2.5秒;(2)动点M出发0.2秒或3秒或4秒或6.8秒时,M、N两点之间的距离刚好为1个单位长度.
解:(1)设点N追上点M需要x秒,
根据题意得:,
解得:.
答:点N追上点M需要2.5秒.
(2)要分四种情况讨论:
设点M出发t秒后,M、N两点之间的距离刚好为1个单位长度,则:
①当点M出发不到1秒,点N还未出发时,M、N两点间距离为1,
由题意得,解得;
②当点M出发1秒后,点N追上动点M之前,M、N两点间距离为1,
由题意得:,
解得:;
③当点M出发1秒后,点N追上点M之后,M、N两点间距离为1,
由题意得:,
解得:;
④当点N到达B点停止运动后,M、N两点间距离为1,
由题意得:,,
解得:,符合题意
答:动点M出发0.2秒或3秒或4秒或6.8秒时,M、N两点之间的距离刚好为1个单位长度.
21.(1)264
km/h;(2)720
km.
解:(1)设无风时飞机的平均航速是x
km/h,
依题意得:2.5×(x+24)=3×(x-24),
解得:x=264,
答:无风时飞机的平均航速是264
km/h.
(2)由(1)知,无风时飞机的平均航速是264千米/时,则
3×(264-24)=720(km),
答:两机场之间的航程是720
km.
22.(1)第三圈弯道比第一圈弯道长15米,第八圈长453米;(2)小王的速度为,老师的速度为.
解:(1)根据题意得,第三圈弯道比第一圈弯道长:
(米);
第八圈长:(米)
答:第三圈弯道比第一圈弯道长15米,第八圈长453米.
(2)由于两人是第一次相遇,教练的速度更快,且是在直道上两人相遇,
那么两人一定在左边的直道上相遇,
两人的总路程刚好是第一圈的长度加上两个半圆赛道长度的差:
(米)
设小王的速度为,则老师的速度为
答:小王的速度为,老师的速度为.
一、单选题
1.方方早上骑自行车上学,中途因道路施工推车步行了一段路,到学校共用时15分钟.如果他骑自行车的平均速度是每分钟250米,推车步行的平均速度是每分钟80米,他家离学校的路程是2900米,设他推车步行的时间为分钟,那么可列出的方程是(
)
A.
B.
C.
D.
2.小亮原计划骑车以10千米/时的速度由A地去B地,这样就可以在规定时间到达B地,但他因故比原计划晚出发15分钟,只好以15千米/时的速度前进,结果比规定时间早到6分钟,若设A,B两地间的距离为x千米,则根据题意列出的方程正确的为(
)
A.+15+6
B.
C.
D.
3.甲、乙两人分别从两地同时骑自行车相向而行,2小时后在途中相遇,相遇后,甲、乙骑自行车的速度都提高了1千米/小时,当甲到达地后立刻以原路和提高后的速度向地返行,乙到达地后也立刻以原路和提高后的速度向地返行.甲、乙两人在开始
出发后的5小时36分钟又再次相遇,则两地的距离是(
)
A.24千米
B.30千米
C.32千米
D.36千米
4.轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是(
)
A.
B.
C.
D.
5.一辆汽车从甲地行驶到乙地,第一小时行驶了全程的,第二小时行驶了全程的,此时离乙地还有150千米的路程,设甲、乙两地间的距离为千米,则下列方程正确的是(
)
A.
B.
C.
D.
6.我国元朝的数学著作《算学启蒙》记载:良马日行二百四十里,驽马日行一百五十里,两马同地出发,驽马先行一十二日,问良马几何追及之?其大意是:良马每天跑里,驽马每天跑里.
良马和驽马从同地出发,驽马先走天,问良马追上驽马的时间为多少天?若设良马追上驽马的时间为天,则可列方程为(
)
A.
B.
C.
D.
7.某铁路桥长1200m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.则火车的长度为(
)
A.180m
B.200m
C.240m
D.250m
8.小明从家里骑自行车到学校,每小时骑,可早到10分钟,每小时骑就会迟到5分钟.他家到学校的路程是多少?设他家到学校的路程是,则据题意列出的方程是(
)
A.
B.
C.
D.
9.甲、乙两人从同一地点出发,如果甲先出发2小时后,乙从后面追赶,那么当乙追上甲时,下面说法正确的是(
)
A.乙比甲多走了2小时
B.乙走的路程比甲多
C.甲、乙所用的时间相等
D.甲、乙所走的路程相等
10.甲、乙两人在长为25米泳池内始终以匀速游泳,两人同时从起点出发,触壁后原路返回,如是往返;甲的速度是1米/秒,乙的速度是0.6米/秒,那么第十次迎面相遇时他们离起点(
)
A.7.5米
B.10米
C.12米
D.12.5米
11.甲、乙两名运动员在圆形跑道上从点同时出发,并按相反方向匀速跑步,甲的速度为每秒6米,乙的速度为每秒7米,当他们第一次在点再度相遇时跑步就结束.则从他们开始出发(算第一次相遇)到结束(算最后一次相遇)共相遇次数是(
)
A.13
B.14
C.42
D.43
12.小明和小亮进行100米赛跑,两人在同一起跑线上,结果第一次比赛时小明胜10米;在进行第二次比赛时,小明的起跑线比原来起跑线推后10米,如果两次他们速度不变,则第二次结果(
)胜.
A.小亮胜
B.小明胜
C.同时到达
D.不能确定
二、填空题
13.一条船顺流航行,每小时行驶20千米;逆流航行,每小时行驶16千米若水的流速与船在静水中的速度都是不变的,则轮船在静水中的速度为______________千米/小时.
14.一人步行从甲地去乙地,第一天行若干千米,自第二天起,每一天都比前一天多走同样的路程,这样10天可以到达乙地;如果每天都以第一天所行的相同路程步行,用15天才能到达乙地;如果每天都以第一种走法的最后一天所行的路程步行到乙地,需要______天.
15.小华和小明周末到北京三山五园绿道骑行.他们按设计好的同一条线路同时出发,小华每小时骑行,小明每小时骑行,他们完成全部行程所用的时间,小明比小华多半小时.设他们这次骑行线路长为,依题意,可列方程为__________.
16.甲、乙二人赛跑,每秒钟甲比乙所跑的路程多,现在甲在乙后面24米所处同时启程,15秒钟后,甲已到终点,乙落后甲6米,则甲跑过的距离为______.
17.一列慢车和一列快车都从站出发到站,它们的速度分别是60千米/时.100千米/时,慢车早发车半小时,结果快车到达站时,慢车刚到达离站50千米的站(站在.两站之间),则A.两站之间的距离是_____千米.
三、解答题
18.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”其意思为:速度快的人走100步,速度慢的人只走60步;现速度慢的人先走100步,速度快的人去追赶.问:速度快的人要走多少步才能追到速度慢的人?
19.甲、乙两列火车从A、B两地相向而行,乙车比甲车早发车,甲车比乙车速度每小时快,甲车发车两小时恰好与乙车相遇,相遇后为了错车,甲车放慢了速度,以它原来的速度行驶;而乙车加快了速度,以它原来的倍飞速行驶,结果后,两车距离又等于A、B两地之间的距离,求两车相遇前速度及A、B两地之间的距离.
20.在数轴上,点A、B分别对应实数和25,点M从A点出发,以每秒5个单位长度的速度沿数轴向右匀速运动;点N从A点以每秒7个单位长度的速度向右匀速运动;M,N两点到达B点后均停止运动;若点M出发1秒后点N才出发.
(1)点N出发后需要多长时间才追上点M?
(2)从点M出发开始到点M停止运动期间,何时M、N两点之间的距离刚好为1个单位长度?
21.在风速为的条件下,一架飞机顺风从机场飞到机场要用,它逆风飞行同样的航线要用.求:
(1)无风时这架飞机在这一航线的平均航速;
(2)两机场之间的航程.
22.据国际田联《田径场地设施标准手册》,400米标准跑道由两个平行的直道和两个半径相等的弯道组成,有8条跑道,每条跑道宽1.2米,直道长87米;跑道的弯道是半圆形,环形跑道第一圈(最内圈)弯道半径为35.00米到38.00米之间.
某校据国际田联标准和学校场地实际,建成第一圈弯道半径为36米的标准跑道.小王同学计算了各圈的长:
第一圈长:87×2+2π(36+1.2×0)≈400(米);
第二圈长:87×2+2π(36+1.2×1)≈408(米);
第三圈长:87×2+2π(36+1.2×2)≈415(米);
……
请问:
(1)第三圈半圆形弯道长比第一圈半圆形弯道长多多少米?小王计算的第八圈长是多少?
(2)小王紧靠第一圈边线逆时针跑步、邓教练紧靠第三圈边线顺时针骑自行车(均以所靠边线长计路程),在如图的起跑线同时出发,经过20秒两人在直道第一次相遇.若邓教练平均速度是小王平均速度的2倍,求他们的平均速度各是多少?
(注:在同侧直道,过两人所在点的直线与跑道边线垂直时,称两人直道相遇)
参考答案
1.A
解:设他推车步行的时间为分钟,骑自行车上学时间为(15-)分钟,
根据题意得:80x+250(15-)=2900,
变形得:250(15-x
)=2900-80x,.
故选择:A.
2.B
解:设A、B两地间的路程为x千米,
根据题意,得.
故选:B.
3.D
解:设第一次相遇时,甲、乙的速度和为xkm/h,
5小时36分钟=5(小时)
由题意可得:2×2x=(5-2)(x+2),
解得:x=18,
∴A、B两地的距离=2×18=36(km),
故选:D.
4.A
解:设A港和B港相距x千米,
根据题意得:.
故选:A.
5.C
解:由已知得:第一个小时行驶路程为,第二个小时行驶路程为,
故:,
整理得:.
故选:C.
6.B
解:设良马x天可以追上驽马,
依题意,得:240x=150(x+12).
故选:B.
7.C
解:设火车的长度为xm,
依题意,得:
,
解得:x=240.
故选:C.
8.A
解:设小明家到学校的路程是,根据题意列方程为:
故选A.
9.D
解:甲先出发2小时,甲多用时2小时。从同一地点出发,追到表示路程相等,
故选:D.
10.D
解:根据题意,画出图形可知:甲乙每迎面相遇一次,两人共行驶25×2=50米,
∴第十次迎面相遇时的总路程为50×10=500米
∴甲行驶的时间为500÷(1+)=s
∴甲行驶的路程为×1=米
∵一个来回共50米
∴÷50≈6个来回
∴此时距离出发点-50×6=米
故选D.
11.B
解:设路程为x,相向而行相遇时间=,相背而行相遇时间=,
根据题意可知最后相遇在A点时相遇次数=÷=13次,
则从他们开始出发(算第一次相遇)到结束(算最后一次相遇)共相遇次数=13+1=14次.
故选B.
12.B
解:设小明用的时间为t,则速度为v1=,
小亮的速度v2=,
第2次比赛时,s1′=100m+10m=110m,s2′=100m,
因为速度不变,所以小明用的时间:t1′=,
小亮用的时间:t2′=,
因为<t,即t1′<t2′,因此还是小明先到达终点,
故选:B.
13.18
解:设轮船在静水中的速度为千米小时,则水流速度为千米小时,
由题意可得:,
解得:,
轮船在静水中的速度为18千米小时,
故答案为:18.
14.7.5
解:设a是第一次第一天走的路程,b是第二天起每天多走的路程,x是所求的天数.则根据题意,得
15a=a+(a+b)+(a+2b)+(a+3b)+(a+4b)+(a+5b)+(a+6b)+(a+7b)+(a+8b)+(a+9b)=10a+45b,
∴15a=10a+45b,
∴5a=45b,
∴a=9b,
又∵15a=x(a+9b)
∴15a=x(a+a),解得
x=7.5
(天).
故答案为:7.5.
15.
解:设他们这次骑行线路长为,则小华完成全部行程的时间为小时,小明完成全部行程的时间为小时,
由题意得,
故答案为:.
16.180米
解:设乙的速度是v米/秒,则甲的速度是(1+)v米/秒,根据题意得:
(1+)v×15﹣15v=24+6,解得:v=10,
所以甲的速度是:10×(1+)=12(米/秒),
则甲跑的路程是:12×15=180米.
故答案为:180米.
17.200
解:设快车从A站出发x小时到达B站,则慢车出发了(x+0.5)小时,依题意列方程得:
60(x+0.5)+50=100x
解得:x=2
即快车从A站出发2小时到达B站,因此A、B两站之间的距离为100×2=200千米,
故答案为:200
18.250步
解:设速度快的人追到速度慢的人所用时间为t,
根据题意列方程得:100t=60t+100,
解得t=2.5,
2.5×100=250(步),
答:速度快的人要走250步才能追到速度慢的人.
19.相遇前甲车的速度为90km/h,乙车的速度为60km/h,A、B两地的距离为360km
解:设两车相遇前乙车的速度为xkm/h,则甲车的速度为km/h,
根据题意得:,
解得:,
,.
答:两车相遇前甲车的速度为90km/h,乙车的速度为60km/h,、两地的距离为360km.
20.(1)点N追上点M需要2.5秒;(2)动点M出发0.2秒或3秒或4秒或6.8秒时,M、N两点之间的距离刚好为1个单位长度.
解:(1)设点N追上点M需要x秒,
根据题意得:,
解得:.
答:点N追上点M需要2.5秒.
(2)要分四种情况讨论:
设点M出发t秒后,M、N两点之间的距离刚好为1个单位长度,则:
①当点M出发不到1秒,点N还未出发时,M、N两点间距离为1,
由题意得,解得;
②当点M出发1秒后,点N追上动点M之前,M、N两点间距离为1,
由题意得:,
解得:;
③当点M出发1秒后,点N追上点M之后,M、N两点间距离为1,
由题意得:,
解得:;
④当点N到达B点停止运动后,M、N两点间距离为1,
由题意得:,,
解得:,符合题意
答:动点M出发0.2秒或3秒或4秒或6.8秒时,M、N两点之间的距离刚好为1个单位长度.
21.(1)264
km/h;(2)720
km.
解:(1)设无风时飞机的平均航速是x
km/h,
依题意得:2.5×(x+24)=3×(x-24),
解得:x=264,
答:无风时飞机的平均航速是264
km/h.
(2)由(1)知,无风时飞机的平均航速是264千米/时,则
3×(264-24)=720(km),
答:两机场之间的航程是720
km.
22.(1)第三圈弯道比第一圈弯道长15米,第八圈长453米;(2)小王的速度为,老师的速度为.
解:(1)根据题意得,第三圈弯道比第一圈弯道长:
(米);
第八圈长:(米)
答:第三圈弯道比第一圈弯道长15米,第八圈长453米.
(2)由于两人是第一次相遇,教练的速度更快,且是在直道上两人相遇,
那么两人一定在左边的直道上相遇,
两人的总路程刚好是第一圈的长度加上两个半圆赛道长度的差:
(米)
设小王的速度为,则老师的速度为
答:小王的速度为,老师的速度为.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
