24.2.1 点和圆的位置关系 (含答案)
文档属性
| 名称 | 24.2.1 点和圆的位置关系 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 00:00:00 | ||
图片预览




文档简介
24.2 点和圆、直线和圆的位置关系
24.2.1 点和圆的位置关系
一、选择题
1.☉O的直径为4,若点A到圆心O的距离为3,则
(
)
A.点A在☉O外
B.点A在☉O上
C.点A在☉O内
D.点A与☉O的位置关系不能确定
2.已知☉O的半径为6
cm,若P是☉O内的一点,则线段OP的长度可能为
(
)
A.5
cm
B.6
cm
C.9
cm
D.12
cm
3.若点A在☉O内,点B在☉O外,OA=3,OB=5,则☉O的半径r的取值范围是
(
)
A.0B.2C.3D.r>5
4.确定一个圆的条件是
(
)
A.已知圆心
B.已知半径
C.过三个已知点
D.过一个三角形的三个顶点
5.过钝角三角形的三个顶点作圆,其圆心在
(
)
A.三角形内
B.三角形上
C.三角形外
D.以上都有可能
6.用反证法证明“a不大于b”时,第一步应假设( )
A.a>b
B.a=b
C.a≥b
D.a≠b
7.用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时应假设
(
)
A.三角形中有一个内角小于或等于60°
B.三角形中有两个内角小于或等于60°
C.三角形中有三个内角小于或等于60°
D.三角形中没有一个内角小于或等于60°
8.若☉A的半径为5,圆心A的坐标是(1,2),点P的坐标是(5,2),那么点P的位置为
(
)
A.在☉A内
B.在☉A上
C.在☉A外
D.不能确定
9.用反证法证明“在△ABC中,∠A,∠B的对边分别是a,b,若∠A>∠B,则a>b.”第一步应假设
(
)
A.aB.a=b
C.a≤b
D.a≥b
10.如图,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,☉A的半径为3,那么下列说法正确的是( )
A.点B,点C都在☉A内
B.点C在☉A内,点B在☉A外
C.点B在☉A内,点C在☉A外
D.点B,点C都在☉A外
第10题图
第11题图
第12题图
第13题图
11.(2020·陕西)如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A.55°
B.65°
C.60°
D.75°
12.如图,△ABC内接于☉O,∠BAC=30°,BC=8,则☉O的半径为( )
A.4
B.6
C.8
D.12
13.如图,已知☉A的半径为5,圆心A的坐标为(1,0),点B(a,0)在☉A外,则a的取值范围( )
A.a<6
B.a>-4
C.-2D.a<-4或a>6
14.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为
(
)
A.
B.2-2
C.2-2
D.4
第14题图
第15题图
第16题图
15.(2020·泰安)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1
B.+
C.2+1
D.2-
16.(2020·泰安)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( ).
A.4
B.4
C.
D.2
二、填空题
17.设⊙O的半径为r,点P到圆心O的距离OP=d,则有:点P在圆外?d________r;点P在圆上?d________r;点P在圆内?d________r.
18.__________________________的三个点确定一个圆.
19.经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的_________,外接圆的圆心是三角形三条边的__________的交点,叫做这个三角形的__________.
20.对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设
.?
21.如图,☉O为△ABC的外接圆,∠A=60°,BC=2,则☉O的半径为
.?
22.如图,Rt△ABE内接于☉O,半径OD垂直于AB,垂足为C,连接CE.若AB=8,CD=2,则△BCE的面积是
.?
第21题图
第22题图
第23题图
23.如图,△ABC内接于☉O,AD⊥BC于点D,AD=BD.若☉O的半径OB=2,则AC的长为
.?
三、解答题
24.[教材P101习题第2题变式]如图,矩形ABCD的边AB=3
cm,BC=4
cm,以点A为圆心,4
cm为半径作☉A,则点B,C,D分别与☉A有怎样的位置关系?
25.如图,点B在直线AC上,点D在直线AC外,过A,B,C,D四点中的任意3个点,可以画多少个圆?
26.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,DB为半径的圆上,并说明理由.
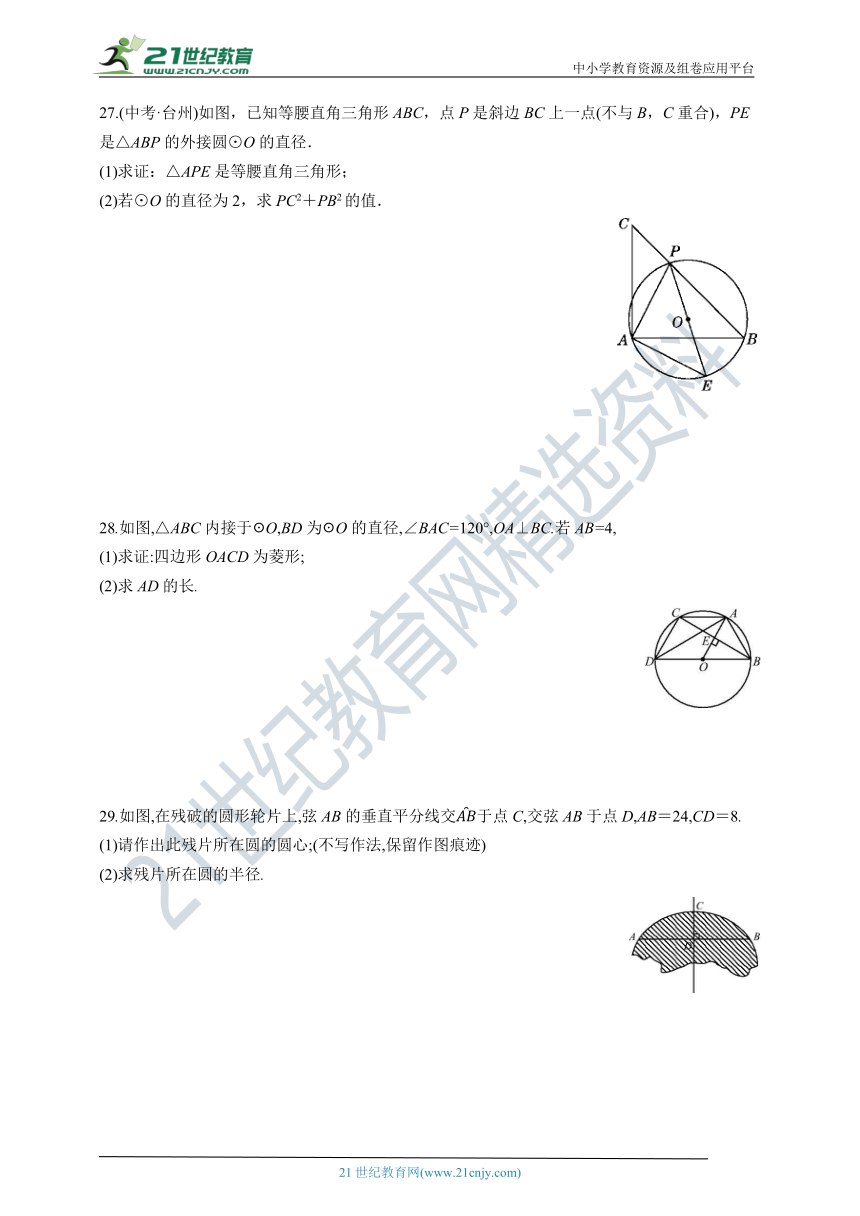
27.(中考·台州)如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求PC2+PB2的值.
28.如图,△ABC内接于☉O,BD为☉O的直径,∠BAC=120°,OA⊥BC.若AB=4,
(1)求证:四边形OACD为菱形;
(2)求AD的长.
29.如图,在残破的圆形轮片上,弦AB的垂直平分线交于点C,交弦AB于点D,AB=24,CD=8.
(1)请作出此残片所在圆的圆心;(不写作法,保留作图痕迹)
(2)求残片所在圆的半径.
30.如图,△ABC内接于☉O,∠BAC=45°,AD⊥BC,垂足为D,BD=6,CD=4.
(1)求☉O的半径;
(2)求AD的长.
31.丁丁在求两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=.他还证明了线段P1P2的中点P(x,y)的坐标公式是x=,y=.
请利用上面的信息,解答下面的问题:
如图,在平面直角坐标系中,已知点A(8,0),B(0,6),C(1,7),☉M经过原点O及点A,B.
(1)求☉M的半径及圆心M的坐标;
(2)判断点C与☉M的位置关系,并说明理由.
32.(中考·日照)如图,已知点A(-1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线对应的函数解析式.
(2)在直线BC上方的抛物线上求一点P,使△PBC的面积为1.
(3)在x轴下方且在抛物线的对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点的坐标;若不存在,说明理由.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.☉O的直径为4,若点A到圆心O的距离为3,则
(A)
A.点A在☉O外
B.点A在☉O上
C.点A在☉O内
D.点A与☉O的位置关系不能确定
2.已知☉O的半径为6
cm,若P是☉O内的一点,则线段OP的长度可能为
(A)
A.5
cm
B.6
cm
C.9
cm
D.12
cm
3.若点A在☉O内,点B在☉O外,OA=3,OB=5,则☉O的半径r的取值范围是
(C)
A.0B.2C.3D.r>5
4.确定一个圆的条件是
(D)
A.已知圆心
B.已知半径
C.过三个已知点
D.过一个三角形的三个顶点
5.过钝角三角形的三个顶点作圆,其圆心在
(C)
A.三角形内
B.三角形上
C.三角形外
D.以上都有可能
6.用反证法证明“a不大于b”时,第一步应假设( A )
A.a>b
B.a=b
C.a≥b
D.a≠b
7.用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时应假设
(D)
A.三角形中有一个内角小于或等于60°
B.三角形中有两个内角小于或等于60°
C.三角形中有三个内角小于或等于60°
D.三角形中没有一个内角小于或等于60°
8.若☉A的半径为5,圆心A的坐标是(1,2),点P的坐标是(5,2),那么点P的位置为
(A)
A.在☉A内
B.在☉A上
C.在☉A外
D.不能确定
9.用反证法证明“在△ABC中,∠A,∠B的对边分别是a,b,若∠A>∠B,则a>b.”第一步应假设
(C)
A.aB.a=b
C.a≤b
D.a≥b
10.如图,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,☉A的半径为3,那么下列说法正确的是( D )
A.点B,点C都在☉A内
B.点C在☉A内,点B在☉A外
C.点B在☉A内,点C在☉A外
D.点B,点C都在☉A外
第10题图
第11题图
第12题图
第13题图
11.(2020·陕西)如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A.55°
B.65°
C.60°
D.75°
【点拨】连接CD.
∵∠A=50°,
∴∠CDB=180°-∠A=130°.
∵E是边BC的中点,
∴OD⊥BC.
∴BD=CD.
∴∠ODB=∠ODC=∠BDC=65°.
【答案】B
12.如图,△ABC内接于☉O,∠BAC=30°,BC=8,则☉O的半径为( C )
A.4
B.6
C.8
D.12
13.如图,已知☉A的半径为5,圆心A的坐标为(1,0),点B(a,0)在☉A外,则a的取值范围( D )
A.a<6
B.a>-4
C.-2D.a<-4或a>6
14.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为
(B)
A.
B.2-2
C.2-2
D.4
第14题图
第15题图
第16题图
15.(2020·泰安)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1
B.+
C.2+1
D.2-
【点拨】如图,作A关于y轴的对称点D,连接BD,CD.
∵A(2,0),∴D(-2,0).
∴OA=OD=2.
∵B(0,2),∴OB=2.
∴BD==2.
∵M点是AC的中点,∴AM=CM.
∴OM是△ACD的中位线.
∴OM=DC.
∵BC=1,
∴点C在以B为圆心,1为半径的圆弧上移动.
∴CD≤BD+BC.
∴CD≤2+1.
∴当且仅当D,B,C三点共线时,CD取得最大值为2+1.
∵OM=CD,
∴OM的最大值为+.
【答案】B
16.(2020·泰安)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( ).
A.4
B.4
C.
D.2
【点拨】如图,连接CD.
∵AB=BC,∠BAC=30°,∴∠ACB=∠BAC=30°.
∴∠B=180°-30°-30°=120°.
∴∠D=180°-∠B=60°.
∵AD是直径,∴∠ACD=90°.
∴∠CAD=30°.
∵AD=8,∴CD=AD=4.
∴AC===4.
【答案】B
二、填空题
17.设⊙O的半径为r,点P到圆心O的距离OP=d,则有:点P在圆外?d________r;点P在圆上?d________r;点P在圆内?d________r.
【答案】>;=;<
18.__________________________的三个点确定一个圆.
【答案】不在同一条直线上
19.经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的_________,外接圆的圆心是三角形三条边的__________的交点,叫做这个三角形的__________.
【答案】外接圆;垂直平分线;外心
20.对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设 b与c相交 .?
21.如图,☉O为△ABC的外接圆,∠A=60°,BC=2,则☉O的半径为 2 .?
22.如图,Rt△ABE内接于☉O,半径OD垂直于AB,垂足为C,连接CE.若AB=8,CD=2,则△BCE的面积是 12 .?
第21题图
第22题图
第23题图
23.如图,△ABC内接于☉O,AD⊥BC于点D,AD=BD.若☉O的半径OB=2,则AC的长为 2 .?
三、解答题
24.[教材P101习题第2题变式]如图,矩形ABCD的边AB=3
cm,BC=4
cm,以点A为圆心,4
cm为半径作☉A,则点B,C,D分别与☉A有怎样的位置关系?
解:连接AC.
∵AB=3
cm,BC=AD=4
cm,
∴AC=5
cm,
∴点B在☉A内,点D在☉A上,点C在☉A外.
25.如图,点B在直线AC上,点D在直线AC外,过A,B,C,D四点中的任意3个点,可以画多少个圆?
解:∵点A,B,C在同一条直线上,
∴经过点A,B,D或点A,C,D或点B,C,D分别能画一个圆,即经过A,B,C,D四点中的任意3个点共能画3个圆.
26.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
证明:∵AD为直径,AD⊥BC,
∴.
∴BD=CD.
(2)请判断B,E,C三点是否在以D为圆心,DB为半径的圆上,并说明理由.
解:B,E,C三点在以D为圆心,DB为半径的圆上.理由如下:
由(1)知,∴∠BAD=∠CBD.
又∵BE平分∠ABC,∴∠CBE=∠ABE.
∵∠DBE=∠CBD+∠CBE,
∠DEB=∠BAD+∠ABE,
∴∠DBE=∠DEB.
∴DB=DE.
由(1)知BD=CD,∴DB=DE=DC.
∴B,E,C三点在以D为圆心,DB为半径的圆上.
27.(中考·台州)如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
解:证明:∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°.
∴∠AEP=∠ABC=45°.
∵PE是⊙O的直径,∴∠PAE=90°.
∴∠APE=∠AEP=45°.
∴AP=AE.
∴△APE是等腰直角三角形.
(2)若⊙O的直径为2,求PC2+PB2的值.
解:如图,作PM⊥AC于M,PN⊥AB于N,则四边形PMAN是矩形.
∴PM=AN,易知△PCM,△PNB都是等腰直角三角形.
∴PC=PM,PB=PN.
∴PC2+PB2=2(PM2+PN2)=2(AN2+PN2)=2PA2=PE2=22=4.
28.如图,△ABC内接于☉O,BD为☉O的直径,∠BAC=120°,OA⊥BC.若AB=4,
(1)求证:四边形OACD为菱形;
(2)求AD的长.
解:(1)∵OA⊥BC,∴,
∴∠CDA=∠ADB=∠BDC.
∵∠BDC=180°-120°=60°,∴∠CDA=∠ADB=30°.
∵∠CAD=∠CAB-∠BAD=30°,∴∠CAD=∠ADB,
∴AC∥OD.
又∵∠DCB=∠OEB=90°,∴CD∥OA,
∴四边形OACD为平行四边形.
又∵OA=OD,∴四边形OACD为菱形.
(2)由(1)可知BD=2AB=8,
在Rt△ABD中,AD==4.
29.如图,在残破的圆形轮片上,弦AB的垂直平分线交于点C,交弦AB于点D,AB=24,CD=8.
(1)请作出此残片所在圆的圆心;(不写作法,保留作图痕迹)
(2)求残片所在圆的半径.
解:(1)如图所示,点O即为残片所在圆的圆心.
(2)连接OA.设OA=x.
∵CD=8,AB=24,
∴AD=BD=AB=12,OD=x-8,
在Rt△ADO中,
由勾股定理得x2=122+(x-8)2,解得x=13,
故残片所在圆的半径为13.
30.如图,△ABC内接于☉O,∠BAC=45°,AD⊥BC,垂足为D,BD=6,CD=4.
(1)求☉O的半径;
(2)求AD的长.
解:(1)连接OB,OC.
∵BD=6,CD=4,∴BC=10.
∵∠BOC=2∠BAC=90°,
∴OB=.
(2)连接OA,过点O作OE⊥AD于点E,OF⊥BC于点F,
∴BF=CF=BC=5,∴DF=CF-CD=1.
∵∠BOC=90°,∴OF=BC=5.
∵AD⊥BC,OE⊥AD,OF⊥BC,
∴四边形OFDE为矩形,
∴OE=DF=1,DE=OF=5,
∴在Rt△AOE中,AE==7,
∴AD=AE+DE=12.
31.丁丁在求两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=.他还证明了线段P1P2的中点P(x,y)的坐标公式是x=,y=.
请利用上面的信息,解答下面的问题:
如图,在平面直角坐标系中,已知点A(8,0),B(0,6),C(1,7),☉M经过原点O及点A,B.
(1)求☉M的半径及圆心M的坐标;
(2)判断点C与☉M的位置关系,并说明理由.
解:(1)∵∠AOB=90°,∴AB是☉M的直径.
∵A(8,0),B(0,6),
∴AB==10,
∴☉M的半径为5.
由线段中点坐标公式x=,
得x=4,y=3,∴点M的坐标为(4,3).
(2)点C在☉M上.
理由:∵C(1,7),M(4,3),
∴CM==5,∴点C在☉M上.
32.(中考·日照)如图,已知点A(-1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线对应的函数解析式.
解:把点A(-1,0),B(3,0),C(0,1)的坐标分别代入y=ax2+bx+c,得
解得
∴抛物线对应的函数解析式为y=-x2+x+1.
(2)
在直线BC上方的抛物线上求一点P,使△PBC的面积为1.
解:∵B(3,0),C(0,1),
∴直线BC对应的函数解析式为y=-x+1.
如图,过点P作PE⊥x轴于点E,交BC于D.
设P,则D(x,-x+1).
∴PD=-x2+x+1-=-x2+x.
∴S△PBC=S△PDC+S△PDB=PD(xB-xC)=(3-0)=-x2+x.
又∵S△PBC=1,∴-x2+x=1,
解得x1=1,x2=2.
∴点P的坐标为或(2,1).
(3)在x轴下方且在抛物线的对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点的坐标;若不存在,说明理由.
【思路点拨】作△ABC的外接圆,此圆与对称轴在x轴下方的交点Q即为所求.
存在.
由题可知点Q为△ABC外接圆与抛物线对称轴在x轴下方的交点.
作△ABC的外接圆,设外接圆圆心为M,连接BM,如图所示.
易知线段AC的垂直平分线为直线y=-x,
线段AB的垂直平分线为直线x=1,
∴点M为直线y=-x与直线x=1的交点,
即M(1,-1).
∴MB==.
∴MQ=MB=.
∴yQ=-(1+)=-1-.
∵点Q在直线x=1上,∴xQ=1.
∴Q(1,-1-).
24.2.1 点和圆的位置关系
一、选择题
1.☉O的直径为4,若点A到圆心O的距离为3,则
(
)
A.点A在☉O外
B.点A在☉O上
C.点A在☉O内
D.点A与☉O的位置关系不能确定
2.已知☉O的半径为6
cm,若P是☉O内的一点,则线段OP的长度可能为
(
)
A.5
cm
B.6
cm
C.9
cm
D.12
cm
3.若点A在☉O内,点B在☉O外,OA=3,OB=5,则☉O的半径r的取值范围是
(
)
A.0
4.确定一个圆的条件是
(
)
A.已知圆心
B.已知半径
C.过三个已知点
D.过一个三角形的三个顶点
5.过钝角三角形的三个顶点作圆,其圆心在
(
)
A.三角形内
B.三角形上
C.三角形外
D.以上都有可能
6.用反证法证明“a不大于b”时,第一步应假设( )
A.a>b
B.a=b
C.a≥b
D.a≠b
7.用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时应假设
(
)
A.三角形中有一个内角小于或等于60°
B.三角形中有两个内角小于或等于60°
C.三角形中有三个内角小于或等于60°
D.三角形中没有一个内角小于或等于60°
8.若☉A的半径为5,圆心A的坐标是(1,2),点P的坐标是(5,2),那么点P的位置为
(
)
A.在☉A内
B.在☉A上
C.在☉A外
D.不能确定
9.用反证法证明“在△ABC中,∠A,∠B的对边分别是a,b,若∠A>∠B,则a>b.”第一步应假设
(
)
A.a
C.a≤b
D.a≥b
10.如图,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,☉A的半径为3,那么下列说法正确的是( )
A.点B,点C都在☉A内
B.点C在☉A内,点B在☉A外
C.点B在☉A内,点C在☉A外
D.点B,点C都在☉A外
第10题图
第11题图
第12题图
第13题图
11.(2020·陕西)如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A.55°
B.65°
C.60°
D.75°
12.如图,△ABC内接于☉O,∠BAC=30°,BC=8,则☉O的半径为( )
A.4
B.6
C.8
D.12
13.如图,已知☉A的半径为5,圆心A的坐标为(1,0),点B(a,0)在☉A外,则a的取值范围( )
A.a<6
B.a>-4
C.-2
14.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为
(
)
A.
B.2-2
C.2-2
D.4
第14题图
第15题图
第16题图
15.(2020·泰安)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1
B.+
C.2+1
D.2-
16.(2020·泰安)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( ).
A.4
B.4
C.
D.2
二、填空题
17.设⊙O的半径为r,点P到圆心O的距离OP=d,则有:点P在圆外?d________r;点P在圆上?d________r;点P在圆内?d________r.
18.__________________________的三个点确定一个圆.
19.经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的_________,外接圆的圆心是三角形三条边的__________的交点,叫做这个三角形的__________.
20.对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设
.?
21.如图,☉O为△ABC的外接圆,∠A=60°,BC=2,则☉O的半径为
.?
22.如图,Rt△ABE内接于☉O,半径OD垂直于AB,垂足为C,连接CE.若AB=8,CD=2,则△BCE的面积是
.?
第21题图
第22题图
第23题图
23.如图,△ABC内接于☉O,AD⊥BC于点D,AD=BD.若☉O的半径OB=2,则AC的长为
.?
三、解答题
24.[教材P101习题第2题变式]如图,矩形ABCD的边AB=3
cm,BC=4
cm,以点A为圆心,4
cm为半径作☉A,则点B,C,D分别与☉A有怎样的位置关系?
25.如图,点B在直线AC上,点D在直线AC外,过A,B,C,D四点中的任意3个点,可以画多少个圆?
26.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,DB为半径的圆上,并说明理由.
27.(中考·台州)如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求PC2+PB2的值.
28.如图,△ABC内接于☉O,BD为☉O的直径,∠BAC=120°,OA⊥BC.若AB=4,
(1)求证:四边形OACD为菱形;
(2)求AD的长.
29.如图,在残破的圆形轮片上,弦AB的垂直平分线交于点C,交弦AB于点D,AB=24,CD=8.
(1)请作出此残片所在圆的圆心;(不写作法,保留作图痕迹)
(2)求残片所在圆的半径.
30.如图,△ABC内接于☉O,∠BAC=45°,AD⊥BC,垂足为D,BD=6,CD=4.
(1)求☉O的半径;
(2)求AD的长.
31.丁丁在求两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=.他还证明了线段P1P2的中点P(x,y)的坐标公式是x=,y=.
请利用上面的信息,解答下面的问题:
如图,在平面直角坐标系中,已知点A(8,0),B(0,6),C(1,7),☉M经过原点O及点A,B.
(1)求☉M的半径及圆心M的坐标;
(2)判断点C与☉M的位置关系,并说明理由.
32.(中考·日照)如图,已知点A(-1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线对应的函数解析式.
(2)在直线BC上方的抛物线上求一点P,使△PBC的面积为1.
(3)在x轴下方且在抛物线的对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点的坐标;若不存在,说明理由.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.☉O的直径为4,若点A到圆心O的距离为3,则
(A)
A.点A在☉O外
B.点A在☉O上
C.点A在☉O内
D.点A与☉O的位置关系不能确定
2.已知☉O的半径为6
cm,若P是☉O内的一点,则线段OP的长度可能为
(A)
A.5
cm
B.6
cm
C.9
cm
D.12
cm
3.若点A在☉O内,点B在☉O外,OA=3,OB=5,则☉O的半径r的取值范围是
(C)
A.0
4.确定一个圆的条件是
(D)
A.已知圆心
B.已知半径
C.过三个已知点
D.过一个三角形的三个顶点
5.过钝角三角形的三个顶点作圆,其圆心在
(C)
A.三角形内
B.三角形上
C.三角形外
D.以上都有可能
6.用反证法证明“a不大于b”时,第一步应假设( A )
A.a>b
B.a=b
C.a≥b
D.a≠b
7.用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时应假设
(D)
A.三角形中有一个内角小于或等于60°
B.三角形中有两个内角小于或等于60°
C.三角形中有三个内角小于或等于60°
D.三角形中没有一个内角小于或等于60°
8.若☉A的半径为5,圆心A的坐标是(1,2),点P的坐标是(5,2),那么点P的位置为
(A)
A.在☉A内
B.在☉A上
C.在☉A外
D.不能确定
9.用反证法证明“在△ABC中,∠A,∠B的对边分别是a,b,若∠A>∠B,则a>b.”第一步应假设
(C)
A.a
C.a≤b
D.a≥b
10.如图,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,☉A的半径为3,那么下列说法正确的是( D )
A.点B,点C都在☉A内
B.点C在☉A内,点B在☉A外
C.点B在☉A内,点C在☉A外
D.点B,点C都在☉A外
第10题图
第11题图
第12题图
第13题图
11.(2020·陕西)如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A.55°
B.65°
C.60°
D.75°
【点拨】连接CD.
∵∠A=50°,
∴∠CDB=180°-∠A=130°.
∵E是边BC的中点,
∴OD⊥BC.
∴BD=CD.
∴∠ODB=∠ODC=∠BDC=65°.
【答案】B
12.如图,△ABC内接于☉O,∠BAC=30°,BC=8,则☉O的半径为( C )
A.4
B.6
C.8
D.12
13.如图,已知☉A的半径为5,圆心A的坐标为(1,0),点B(a,0)在☉A外,则a的取值范围( D )
A.a<6
B.a>-4
C.-2
14.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为
(B)
A.
B.2-2
C.2-2
D.4
第14题图
第15题图
第16题图
15.(2020·泰安)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1
B.+
C.2+1
D.2-
【点拨】如图,作A关于y轴的对称点D,连接BD,CD.
∵A(2,0),∴D(-2,0).
∴OA=OD=2.
∵B(0,2),∴OB=2.
∴BD==2.
∵M点是AC的中点,∴AM=CM.
∴OM是△ACD的中位线.
∴OM=DC.
∵BC=1,
∴点C在以B为圆心,1为半径的圆弧上移动.
∴CD≤BD+BC.
∴CD≤2+1.
∴当且仅当D,B,C三点共线时,CD取得最大值为2+1.
∵OM=CD,
∴OM的最大值为+.
【答案】B
16.(2020·泰安)如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( ).
A.4
B.4
C.
D.2
【点拨】如图,连接CD.
∵AB=BC,∠BAC=30°,∴∠ACB=∠BAC=30°.
∴∠B=180°-30°-30°=120°.
∴∠D=180°-∠B=60°.
∵AD是直径,∴∠ACD=90°.
∴∠CAD=30°.
∵AD=8,∴CD=AD=4.
∴AC===4.
【答案】B
二、填空题
17.设⊙O的半径为r,点P到圆心O的距离OP=d,则有:点P在圆外?d________r;点P在圆上?d________r;点P在圆内?d________r.
【答案】>;=;<
18.__________________________的三个点确定一个圆.
【答案】不在同一条直线上
19.经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的_________,外接圆的圆心是三角形三条边的__________的交点,叫做这个三角形的__________.
【答案】外接圆;垂直平分线;外心
20.对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设 b与c相交 .?
21.如图,☉O为△ABC的外接圆,∠A=60°,BC=2,则☉O的半径为 2 .?
22.如图,Rt△ABE内接于☉O,半径OD垂直于AB,垂足为C,连接CE.若AB=8,CD=2,则△BCE的面积是 12 .?
第21题图
第22题图
第23题图
23.如图,△ABC内接于☉O,AD⊥BC于点D,AD=BD.若☉O的半径OB=2,则AC的长为 2 .?
三、解答题
24.[教材P101习题第2题变式]如图,矩形ABCD的边AB=3
cm,BC=4
cm,以点A为圆心,4
cm为半径作☉A,则点B,C,D分别与☉A有怎样的位置关系?
解:连接AC.
∵AB=3
cm,BC=AD=4
cm,
∴AC=5
cm,
∴点B在☉A内,点D在☉A上,点C在☉A外.
25.如图,点B在直线AC上,点D在直线AC外,过A,B,C,D四点中的任意3个点,可以画多少个圆?
解:∵点A,B,C在同一条直线上,
∴经过点A,B,D或点A,C,D或点B,C,D分别能画一个圆,即经过A,B,C,D四点中的任意3个点共能画3个圆.
26.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
证明:∵AD为直径,AD⊥BC,
∴.
∴BD=CD.
(2)请判断B,E,C三点是否在以D为圆心,DB为半径的圆上,并说明理由.
解:B,E,C三点在以D为圆心,DB为半径的圆上.理由如下:
由(1)知,∴∠BAD=∠CBD.
又∵BE平分∠ABC,∴∠CBE=∠ABE.
∵∠DBE=∠CBD+∠CBE,
∠DEB=∠BAD+∠ABE,
∴∠DBE=∠DEB.
∴DB=DE.
由(1)知BD=CD,∴DB=DE=DC.
∴B,E,C三点在以D为圆心,DB为半径的圆上.
27.(中考·台州)如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
解:证明:∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°.
∴∠AEP=∠ABC=45°.
∵PE是⊙O的直径,∴∠PAE=90°.
∴∠APE=∠AEP=45°.
∴AP=AE.
∴△APE是等腰直角三角形.
(2)若⊙O的直径为2,求PC2+PB2的值.
解:如图,作PM⊥AC于M,PN⊥AB于N,则四边形PMAN是矩形.
∴PM=AN,易知△PCM,△PNB都是等腰直角三角形.
∴PC=PM,PB=PN.
∴PC2+PB2=2(PM2+PN2)=2(AN2+PN2)=2PA2=PE2=22=4.
28.如图,△ABC内接于☉O,BD为☉O的直径,∠BAC=120°,OA⊥BC.若AB=4,
(1)求证:四边形OACD为菱形;
(2)求AD的长.
解:(1)∵OA⊥BC,∴,
∴∠CDA=∠ADB=∠BDC.
∵∠BDC=180°-120°=60°,∴∠CDA=∠ADB=30°.
∵∠CAD=∠CAB-∠BAD=30°,∴∠CAD=∠ADB,
∴AC∥OD.
又∵∠DCB=∠OEB=90°,∴CD∥OA,
∴四边形OACD为平行四边形.
又∵OA=OD,∴四边形OACD为菱形.
(2)由(1)可知BD=2AB=8,
在Rt△ABD中,AD==4.
29.如图,在残破的圆形轮片上,弦AB的垂直平分线交于点C,交弦AB于点D,AB=24,CD=8.
(1)请作出此残片所在圆的圆心;(不写作法,保留作图痕迹)
(2)求残片所在圆的半径.
解:(1)如图所示,点O即为残片所在圆的圆心.
(2)连接OA.设OA=x.
∵CD=8,AB=24,
∴AD=BD=AB=12,OD=x-8,
在Rt△ADO中,
由勾股定理得x2=122+(x-8)2,解得x=13,
故残片所在圆的半径为13.
30.如图,△ABC内接于☉O,∠BAC=45°,AD⊥BC,垂足为D,BD=6,CD=4.
(1)求☉O的半径;
(2)求AD的长.
解:(1)连接OB,OC.
∵BD=6,CD=4,∴BC=10.
∵∠BOC=2∠BAC=90°,
∴OB=.
(2)连接OA,过点O作OE⊥AD于点E,OF⊥BC于点F,
∴BF=CF=BC=5,∴DF=CF-CD=1.
∵∠BOC=90°,∴OF=BC=5.
∵AD⊥BC,OE⊥AD,OF⊥BC,
∴四边形OFDE为矩形,
∴OE=DF=1,DE=OF=5,
∴在Rt△AOE中,AE==7,
∴AD=AE+DE=12.
31.丁丁在求两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=.他还证明了线段P1P2的中点P(x,y)的坐标公式是x=,y=.
请利用上面的信息,解答下面的问题:
如图,在平面直角坐标系中,已知点A(8,0),B(0,6),C(1,7),☉M经过原点O及点A,B.
(1)求☉M的半径及圆心M的坐标;
(2)判断点C与☉M的位置关系,并说明理由.
解:(1)∵∠AOB=90°,∴AB是☉M的直径.
∵A(8,0),B(0,6),
∴AB==10,
∴☉M的半径为5.
由线段中点坐标公式x=,
得x=4,y=3,∴点M的坐标为(4,3).
(2)点C在☉M上.
理由:∵C(1,7),M(4,3),
∴CM==5,∴点C在☉M上.
32.(中考·日照)如图,已知点A(-1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线对应的函数解析式.
解:把点A(-1,0),B(3,0),C(0,1)的坐标分别代入y=ax2+bx+c,得
解得
∴抛物线对应的函数解析式为y=-x2+x+1.
(2)
在直线BC上方的抛物线上求一点P,使△PBC的面积为1.
解:∵B(3,0),C(0,1),
∴直线BC对应的函数解析式为y=-x+1.
如图,过点P作PE⊥x轴于点E,交BC于D.
设P,则D(x,-x+1).
∴PD=-x2+x+1-=-x2+x.
∴S△PBC=S△PDC+S△PDB=PD(xB-xC)=(3-0)=-x2+x.
又∵S△PBC=1,∴-x2+x=1,
解得x1=1,x2=2.
∴点P的坐标为或(2,1).
(3)在x轴下方且在抛物线的对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点的坐标;若不存在,说明理由.
【思路点拨】作△ABC的外接圆,此圆与对称轴在x轴下方的交点Q即为所求.
存在.
由题可知点Q为△ABC外接圆与抛物线对称轴在x轴下方的交点.
作△ABC的外接圆,设外接圆圆心为M,连接BM,如图所示.
易知线段AC的垂直平分线为直线y=-x,
线段AB的垂直平分线为直线x=1,
∴点M为直线y=-x与直线x=1的交点,
即M(1,-1).
∴MB==.
∴MQ=MB=.
∴yQ=-(1+)=-1-.
∵点Q在直线x=1上,∴xQ=1.
∴Q(1,-1-).
同课章节目录
