24.4.1 弧长和扇形面积同步练习(含答案)
文档属性
| 名称 | 24.4.1 弧长和扇形面积同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 00:00:00 | ||
图片预览




文档简介
24.4 弧长和扇形面积
第1课时 弧长和扇形面积
一、选择题
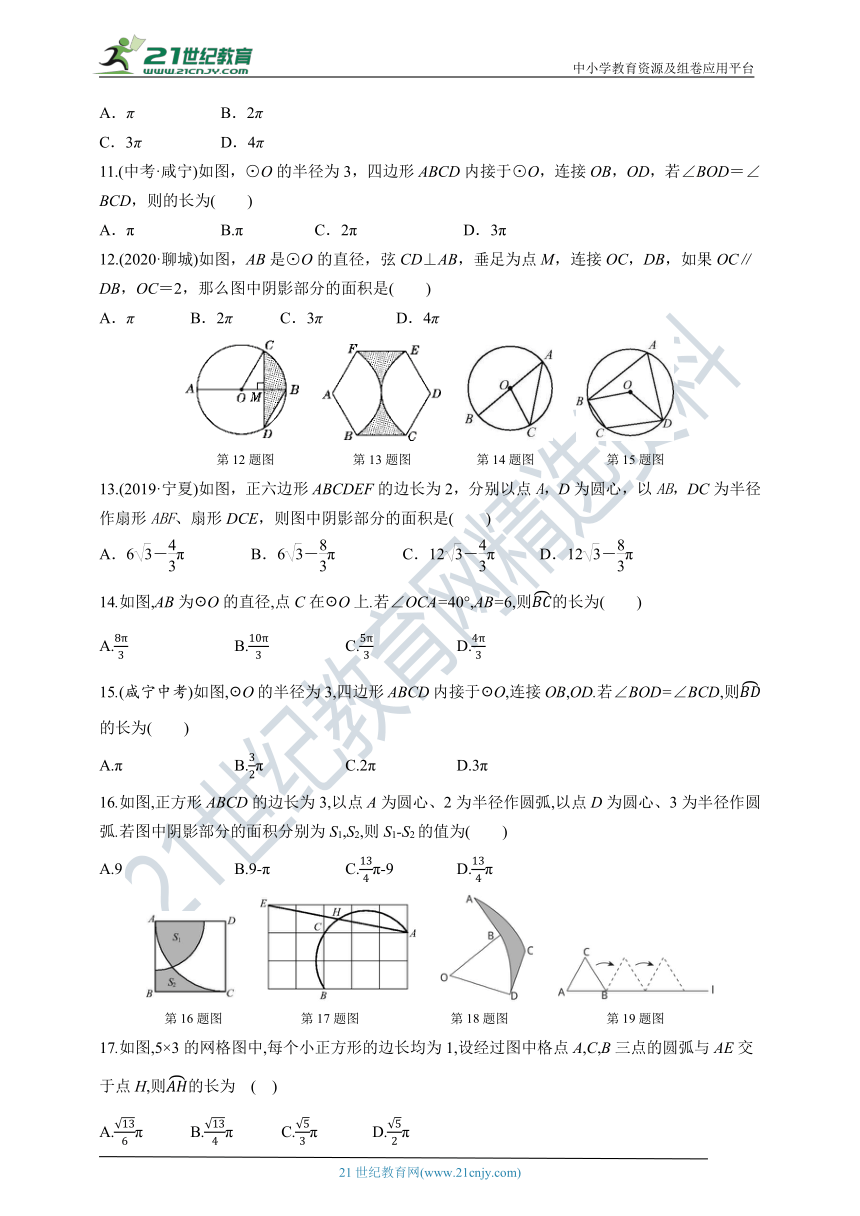
1.如图,☉O的半径为6,☉O上有三点A,B,C,且∠ACB=30°,则的长等于
(
)
A.π
B.2π
C.3π
D.4π
第1题图
第5题图
第10题图
第11题图
2.(2019·温州)若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π
B.2π
C.3π
D.6π
3.有一段长度为2.5π的弧,则此弧所对的圆心角的度数为75°,则这段圆弧所在圆的半径是
(
)
A.3
B.4
C.6
D.12
4.有一条弧的长为2π
cm,半径为2
cm,则这条弧所对的圆心角的度数是
(
)
A.90°
B.120°
C.135°
D.180°
5.如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,AB的长为32
cm,BD的长为14
cm,则的长为
(
)
A.π
cm
B.12π
cm
C.15π
cm
D.36π
cm
6.若扇形的圆心角为90°,半径为6,则该扇形的面积为
(
)
A.
B.3π
C.6π
D.9π
7.如果弧长为4π
cm的扇形面积为16π
cm2,那么该扇形的半径为
(
)
A.8
cm
B.9
cm
C.10
cm
D.11
cm
8.已知一个扇形的半径等于一个圆的半径的2倍,且它的面积等于该已知圆的面积,则这一扇形的圆心角为
(
)
A.60°
B.90°
C.120°
D.150°
9.若钟面上分针的长为1,则从9点到9点15分,分针在钟面上扫过的面积是
(
)
A.π
B.π
C.π
D.π
10.(2020·南充)如图,四个三角形拼成一个风车图形,若AB=2,当风车转动90°,点B运动路径的长度为( )
A.π
B.2π
C.3π
D.4π
11.(中考·咸宁)如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为( )
A.π
B.π
C.2π
D.3π
12.(2020·聊城)如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M,连接OC,DB,如果OC∥DB,OC=2,那么图中阴影部分的面积是( )
A.π
B.2π
C.3π
D.4π
第12题图
第13题图
第14题图
第15题图
13.(2019·宁夏)如图,正六边形ABCDEF的边长为2,分别以点A,D为圆心,以AB,DC为半径作扇形ABF、扇形DCE,则图中阴影部分的面积是( )
A.6-π
B.6-π
C.12-π
D.12-π
14.如图,AB为☉O的直径,点C在☉O上.若∠OCA=40°,AB=6,则的长为( )
A.
B.
C.
D.
15.(咸宁中考)如图,☉O的半径为3,四边形ABCD内接于☉O,连接OB,OD.若∠BOD=∠BCD,则的长为( )
A.π
B.π
C.2π
D.3π
16.如图,正方形ABCD的边长为3,以点A为圆心、2为半径作圆弧,以点D为圆心、3为半径作圆弧.若图中阴影部分的面积分别为S1,S2,则S1-S2的值为( )
A.9
B.9-π
C.π-9
D.π
第16题图
第17题图
第18题图
第19题图
17.如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于点H,则的长为
(
)
A.π
B.π
C.π
D.π
18.如图,AB⊥OB,AB=2,OB=4,把∠ABO绕点O顺时针旋转60°得到∠CDO,则AB扫过的面积(图中阴影部分)为
(
)
A.2
B.2π
C.π
D.π
19.边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为
(
)
A.
B.
C.π
D.
20.(2020·淄博)如图,放置在直线l上的扇形OAB,由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径OA=2,∠AOB=45°,则点O所经过的路径的长是( )
A.2π+2
B.3π
C.
D.+2
第20题图
第21题图
21.(2020·苏州)如图,在扇形OAB中,已知∠AOB=90°,OA=,过的中点C作CD⊥OA,CE⊥OB,垂足分别为D,E,则图中阴影部分的面积为( )
A.π-1
B.
-1
C.π-
D.
-
22.(2020·乐山)在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图,将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′.则图中阴影部分面积为( )
A.
B.
C.
D.π
第22题图
第23题图
23.(2020·遂宁)如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=,则图中阴影部分面积为( )
A.4-
B.2-
C.2-π
D.1-
二、填空题
24.在半径为R的圆中,n°的圆心角所对的弧长为______.
25.由组成圆心角的__________和______________围成的图形叫做扇形;半径为R,圆心角为n°的扇形的面积为____________;若已知扇形的半径为R,弧长为l,则扇形的面积为________.
26.(贵港中考)如图,在Rt△ABC中,∠ACB=90°,AB=4,BC=2,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,则图中阴影部分的面积为________.(结果保留π).
第26题图
第27题图
第29题图
第30题图
第31题图
27.如图,一把直角尺的45°角的顶点A落在☉O上,两边分别交☉O于B,C两点.若☉O的半径为2,则的长为
.?
28.若某扇形花坛的面积为6
m2,半径为3
m,则该扇形花坛的弧长为
m.?
29.如图,AB是☉O的直径,弦CD⊥AB于点E,连接BD,∠ABD=60°,CD=2,则的长为
.?
30.如图,在△ABC中,BC=2,∠B=60°,若把线段BC绕着点B旋转,使得点C落在直线AB上的点D处,旋转角度大于0°且小于180°,那么线段BC扫过的面积等于
.(结果保留π)?
31.(天水中考)如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长是
.?
三、解答题
32.如图,A,B,C三点在半径为1的☉O上,四边形ABCO是菱形,求的长.
33.如图,AB是半圆的直径,C,D是的三等分点,☉O的半径为1.
(1)求的长;
(2)求图中阴影部分的面积.
34.如图,AB是☉O的直径,弦CD交AB于点E,∠ACD=60°,∠ADC=50°.
(1)求∠CEB的度数;
(2)若AD=2,求扇形AOC的面积.
35.如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得BD=CB,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
36.如图,AB是☉O的直径,C,D是☉O上的点,OC∥BD交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
37.(2020·郴州)如图,△ABC内接于⊙O,AB是⊙O的直径.直线l与⊙O相切于点A,在l上取一点D使得DA=DC,线段DC,AB的延长线交于点E.
(1)求证:直线DC是⊙O的切线.
(2)若BC=2,∠CAB=30°,求图中阴影部分的面积(结果保留π).
38.如图,在平面直角坐标系中,直线l的函数解析式为y=x,点O1的坐标为(1,0),以点O1为圆心、O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和围成的弓形面积记为S1;以点O2为圆心、O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围成的弓形面积记为S2;以点O3为圆心、O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和围成的弓形面积记为S3;……按此做法进行下去,求S2021.
39.如图,半圆O的直径AB=6,弦CD的长为3,点C,D在上运动,点D在上运动,且不与点A重合,但点C可与点B重合.
(1)当的长为时,求的长;
(2)取CD的中点M,在CD运动的过程中,求点M到AB的距离的最小值.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,☉O的半径为6,☉O上有三点A,B,C,且∠ACB=30°,则的长等于
(B)
A.π
B.2π
C.3π
D.4π
第1题图
第5题图
第10题图
第11题图
2.(2019·温州)若扇形的圆心角为90°,半径为6,则该扇形的弧长为( C )
A.π
B.2π
C.3π
D.6π
3.有一段长度为2.5π的弧,则此弧所对的圆心角的度数为75°,则这段圆弧所在圆的半径是
(C)
A.3
B.4
C.6
D.12
4.有一条弧的长为2π
cm,半径为2
cm,则这条弧所对的圆心角的度数是
(D)
A.90°
B.120°
C.135°
D.180°
5.如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,AB的长为32
cm,BD的长为14
cm,则的长为
(C)
A.π
cm
B.12π
cm
C.15π
cm
D.36π
cm
6.若扇形的圆心角为90°,半径为6,则该扇形的面积为
(D)
A.
B.3π
C.6π
D.9π
7.如果弧长为4π
cm的扇形面积为16π
cm2,那么该扇形的半径为
(A)
A.8
cm
B.9
cm
C.10
cm
D.11
cm
8.已知一个扇形的半径等于一个圆的半径的2倍,且它的面积等于该已知圆的面积,则这一扇形的圆心角为
(B)
A.60°
B.90°
C.120°
D.150°
9.若钟面上分针的长为1,则从9点到9点15分,分针在钟面上扫过的面积是
(B)
A.π
B.π
C.π
D.π
10.(2020·南充)如图,四个三角形拼成一个风车图形,若AB=2,当风车转动90°,点B运动路径的长度为( A )
A.π
B.2π
C.3π
D.4π
11.(中考·咸宁)如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为( C )
A.π
B.π
C.2π
D.3π
12.(2020·聊城)如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M,连接OC,DB,如果OC∥DB,OC=2,那么图中阴影部分的面积是( B )
A.π
B.2π
C.3π
D.4π
第12题图
第13题图
第14题图
第15题图
13.(2019·宁夏)如图,正六边形ABCDEF的边长为2,分别以点A,D为圆心,以AB,DC为半径作扇形ABF、扇形DCE,则图中阴影部分的面积是( B )
A.6-π
B.6-π
C.12-π
D.12-π
14.如图,AB为☉O的直径,点C在☉O上.若∠OCA=40°,AB=6,则的长为( D )
A.
B.
C.
D.
15.(咸宁中考)如图,☉O的半径为3,四边形ABCD内接于☉O,连接OB,OD.若∠BOD=∠BCD,则的长为( C )
A.π
B.π
C.2π
D.3π
16.如图,正方形ABCD的边长为3,以点A为圆心、2为半径作圆弧,以点D为圆心、3为半径作圆弧.若图中阴影部分的面积分别为S1,S2,则S1-S2的值为( C )
A.9
B.9-π
C.π-9
D.π
第16题图
第17题图
第18题图
第19题图
17.如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于点H,则的长为
(B)
A.π
B.π
C.π
D.π
18.如图,AB⊥OB,AB=2,OB=4,把∠ABO绕点O顺时针旋转60°得到∠CDO,则AB扫过的面积(图中阴影部分)为
(C)
A.2
B.2π
C.π
D.π
19.边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为
(B)
A.
B.
C.π
D.
20.(2020·淄博)如图,放置在直线l上的扇形OAB,由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径OA=2,∠AOB=45°,则点O所经过的路径的长是( )
A.2π+2
B.3π
C.
D.+2
【点拨】如图所示.
第20题图
第21题图
21.(2020·苏州)如图,在扇形OAB中,已知∠AOB=90°,OA=,过的中点C作CD⊥OA,CE⊥OB,垂足分别为D,E,则图中阴影部分的面积为( )
A.π-1
B.
-1
C.π-
D.
-
【点拨】∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=∠AOB=90°.∴四边形CDOE是矩形.
连接OC.
∵点C是的中点,
∴∠AOC=∠BOC.
又∵OC=OC,
∴△COD≌△COE(AAS).
∴OD=OE.
∴矩形CDOE是正方形.
∵OC=OA=,∴OE=1.
∴S阴影=S扇形OAB-S正方形CDOE=-1×1=-1.
【答案】B
22.(2020·乐山)在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图,将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′.则图中阴影部分面积为( )
A.
B.
C.
D.π
第22题图
第23题图
【点拨】∵∠ABC=90°,∠BAC=30°,BC=1,
∠BAB′=90°,
∴∠CAB′=60°,AC=2BC=2.
∴AB=.
∴S阴影=--×1×=.
【答案】B
23.(2020·遂宁)如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=,则图中阴影部分面积为( )
A.4-
B.2-
C.2-π
D.1-
【点拨】如图,连接OD,过点O作OH⊥AC于点H.
∵∠C=90°,AC=BC,
∴∠B=∠CAB=45°.
∵⊙O与BC相切于点D,
∴OD⊥BC.
∴四边形ODCH为矩形.
∴OH=CD=.
在Rt△OAH中,∠OAH=45°,
∴OA=OH=2.
∴OD=OA=2.
在Rt△OBD中,∠B=45°,
∴∠BOD=45°,BD=OD=2.
∴S阴影=S△OBD-S扇形ODE=×2×2-=2-.
【答案】B
二、填空题
24.在半径为R的圆中,n°的圆心角所对的弧长为______.
【答案】
25.由组成圆心角的__________和______________围成的图形叫做扇形;半径为R,圆心角为n°的扇形的面积为____________;若已知扇形的半径为R,弧长为l,则扇形的面积为________.
【答案】两条半径;圆心角所对的弧;;lR
26.(贵港中考)如图,在Rt△ABC中,∠ACB=90°,AB=4,BC=2,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,则图中阴影部分的面积为________.(结果保留π).
【答案】4π
第26题图
第27题图
第29题图
第30题图
第31题图
27.如图,一把直角尺的45°角的顶点A落在☉O上,两边分别交☉O于B,C两点.若☉O的半径为2,则的长为 π .?
28.若某扇形花坛的面积为6
m2,半径为3
m,则该扇形花坛的弧长为 4 m.?
29.如图,AB是☉O的直径,弦CD⊥AB于点E,连接BD,∠ABD=60°,CD=2,则的长为?π .?
30.如图,在△ABC中,BC=2,∠B=60°,若把线段BC绕着点B旋转,使得点C落在直线AB上的点D处,旋转角度大于0°且小于180°,那么线段BC扫过的面积等于?π .(结果保留π)?
31.(天水中考)如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长是 4π .?
三、解答题
32.如图,A,B,C三点在半径为1的☉O上,四边形ABCO是菱形,求的长.
解:连接OB.
∵四边形OABC是菱形,
∴OA=AB=OB=OC=BC,
∴△AOB,△BOC都是等边三角形,
∴∠AOB=∠BOC=60°,∴∠AOC=120°,
∴.
33.如图,AB是半圆的直径,C,D是的三等分点,☉O的半径为1.
(1)求的长;
(2)求图中阴影部分的面积.
解:(1)∵C,D是的三等分点,∴∠COD=60°,
∴的长l=.
(2)图中阴影部分的面积=.
34.如图,AB是☉O的直径,弦CD交AB于点E,∠ACD=60°,∠ADC=50°.
(1)求∠CEB的度数;
(2)若AD=2,求扇形AOC的面积.
解:(1)连接BC.∵AB是☉O的直径,∴∠ACB=90°.
又∵∠ABC=∠ADC=50°,∴∠BAC=40°,
∴∠CEB=∠ACD+∠BAC=60°+40°=100°.
(2)连接BD,OC,则∠AOC=2∠ADC=100°.
∵∠BAD=∠BCD=30°,∠ADB=90°,AD=2,
∴AB=4,∴AO=2,∴扇形AOC的面积=.
35.如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得BD=CB,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
证明:连接BO.
∵∠ACB=30°,OB=OC,∴∠OBC=∠OCB=30°.
∵DE⊥AC,CB=BD.
∴BE=CD=BC.
∴∠BEC=∠BCE=30°.
∴在△BCE中,∠EBC=180°-∠BEC-∠BCE=120°.
∴∠EBO=∠EBC-∠OBC=120°-30°=90°.
∴BE是⊙O的切线.
(2)当BE=3时,求图中阴影部分的面积.
解:当BE=3时,BC=3.
∵AC为⊙O的直径,∴∠ABC=90°.
又∵∠ACB=30°,∴AB=AC.
∵AB2+BC2=AC2,∴AB=.
∴AC=2.∴AO=.
∴S阴影=S半圆形-SRt△ABC=π×AO2-AB×BC=π×3-××3=π-
.
36.如图,AB是☉O的直径,C,D是☉O上的点,OC∥BD交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
解:(1)∵AB是☉O的直径,∴∠ADB=90°.
∵OC∥BD,O为AB的中点,
∴OE为△ABD的中位线,∴AE=ED.
(2)连接OD.
∵OC∥BD,∠CBD=30°,∴∠OCB=∠CBD=30°.
∵OC=OB,∴∠OBC=∠OCB=30°,
∴∠AOC=∠OCB+∠OBC=60°.
∵∠COD=2∠CBD=60°,∴∠AOD=120°.
由(1)可知∠AEO=90°,
∴∠AOE=60°,∠OAE=30°.
∵AB=6,∴OA=,
∴S阴影=S扇形AOD-S△AOD=.
37.(2020·郴州)如图,△ABC内接于⊙O,AB是⊙O的直径.直线l与⊙O相切于点A,在l上取一点D使得DA=DC,线段DC,AB的延长线交于点E.
(1)求证:直线DC是⊙O的切线.
证明:如图,连接OC.
∵AB是⊙O的直径,直线l与⊙O相切于点A,∴∠DAB=90°.
∵DA=DC,OA=OC,
∴∠DAC=∠DCA,∠OAC=∠OCA.
∴∠DCA+∠OCA=∠DAC+∠OAC,
即∠DCO=∠DAO=90°.
∴OC⊥DC.
∴直线DC是⊙O的切线.
(2)若BC=2,∠CAB=30°,求图中阴影部分的面积(结果保留π).
【思路点拨】连接OC,将阴影部分的面积转化为△OCE与扇形OCB的面积之差.
解:∵∠CAB=30°,
∴∠BOC=2∠CAB=60°.
又∵OC=OB,∴△COB是等边三角形.
∴OC=OB=BC=2.
在Rt△OCE中,∠EOC=60°,
∴∠E=30°.
∴OE=2OC=4.
∴CE=2.
∴S阴影=S△OCE-S扇形OCB=×2×2-=2-.
38.如图,在平面直角坐标系中,直线l的函数解析式为y=x,点O1的坐标为(1,0),以点O1为圆心、O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和围成的弓形面积记为S1;以点O2为圆心、O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围成的弓形面积记为S2;以点O3为圆心、O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和围成的弓形面积记为S3;……按此做法进行下去,求S2021.
解:连接P1O1,P2O2,P3O3,P4O4,…,
∵P1是☉O1上的点,∴P1O1=O1O2.
∵直线l的解析式为y=x,∴∠P1OO1=30°,
∴∠P1O1O2=60°,∴△O1P1O2是等边三角形,
∴△O1P1O2的边长=1,∴△O1P1O2的面积=,
∴S1=π-,
同理S2=π-,S3=π-4,S4=-16π-42,…
∴Sn=π-4n-2,∴S2021=π-42019.
39.如图,半圆O的直径AB=6,弦CD的长为3,点C,D在上运动,点D在上运动,且不与点A重合,但点C可与点B重合.
(1)当的长为时,求的长;
(2)取CD的中点M,在CD运动的过程中,求点M到AB的距离的最小值.
解:(1)连接OD,OC.
∵AB=6,CD=3,
∴OC=OD=AB=CD=3,
∴△CDO是等边三角形,∴∠COD=60°,
∴=π.
∵×6π=3π,
∴.
(2)过点M作ME⊥AB于点E,连接OM.
∵CD=3,∴DM=.
∵△CDO是等边三角形,M为CD的中点,
∴∠OMD=90°,∠DOM=∠COM=30°,
∴在Rt△OMD中,OM=.
∵在Rt△DME中,ME2=OM2-OE2,
∴若ME取最小值,则只需要OE最大即可.
当点C与点B重合时,此时OE最大,如图.
∵∠MOC=30°,OM=,
∴ME=,
即点M到AB的距离的最小值为.
第1课时 弧长和扇形面积
一、选择题
1.如图,☉O的半径为6,☉O上有三点A,B,C,且∠ACB=30°,则的长等于
(
)
A.π
B.2π
C.3π
D.4π
第1题图
第5题图
第10题图
第11题图
2.(2019·温州)若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π
B.2π
C.3π
D.6π
3.有一段长度为2.5π的弧,则此弧所对的圆心角的度数为75°,则这段圆弧所在圆的半径是
(
)
A.3
B.4
C.6
D.12
4.有一条弧的长为2π
cm,半径为2
cm,则这条弧所对的圆心角的度数是
(
)
A.90°
B.120°
C.135°
D.180°
5.如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,AB的长为32
cm,BD的长为14
cm,则的长为
(
)
A.π
cm
B.12π
cm
C.15π
cm
D.36π
cm
6.若扇形的圆心角为90°,半径为6,则该扇形的面积为
(
)
A.
B.3π
C.6π
D.9π
7.如果弧长为4π
cm的扇形面积为16π
cm2,那么该扇形的半径为
(
)
A.8
cm
B.9
cm
C.10
cm
D.11
cm
8.已知一个扇形的半径等于一个圆的半径的2倍,且它的面积等于该已知圆的面积,则这一扇形的圆心角为
(
)
A.60°
B.90°
C.120°
D.150°
9.若钟面上分针的长为1,则从9点到9点15分,分针在钟面上扫过的面积是
(
)
A.π
B.π
C.π
D.π
10.(2020·南充)如图,四个三角形拼成一个风车图形,若AB=2,当风车转动90°,点B运动路径的长度为( )
A.π
B.2π
C.3π
D.4π
11.(中考·咸宁)如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为( )
A.π
B.π
C.2π
D.3π
12.(2020·聊城)如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M,连接OC,DB,如果OC∥DB,OC=2,那么图中阴影部分的面积是( )
A.π
B.2π
C.3π
D.4π
第12题图
第13题图
第14题图
第15题图
13.(2019·宁夏)如图,正六边形ABCDEF的边长为2,分别以点A,D为圆心,以AB,DC为半径作扇形ABF、扇形DCE,则图中阴影部分的面积是( )
A.6-π
B.6-π
C.12-π
D.12-π
14.如图,AB为☉O的直径,点C在☉O上.若∠OCA=40°,AB=6,则的长为( )
A.
B.
C.
D.
15.(咸宁中考)如图,☉O的半径为3,四边形ABCD内接于☉O,连接OB,OD.若∠BOD=∠BCD,则的长为( )
A.π
B.π
C.2π
D.3π
16.如图,正方形ABCD的边长为3,以点A为圆心、2为半径作圆弧,以点D为圆心、3为半径作圆弧.若图中阴影部分的面积分别为S1,S2,则S1-S2的值为( )
A.9
B.9-π
C.π-9
D.π
第16题图
第17题图
第18题图
第19题图
17.如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于点H,则的长为
(
)
A.π
B.π
C.π
D.π
18.如图,AB⊥OB,AB=2,OB=4,把∠ABO绕点O顺时针旋转60°得到∠CDO,则AB扫过的面积(图中阴影部分)为
(
)
A.2
B.2π
C.π
D.π
19.边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为
(
)
A.
B.
C.π
D.
20.(2020·淄博)如图,放置在直线l上的扇形OAB,由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径OA=2,∠AOB=45°,则点O所经过的路径的长是( )
A.2π+2
B.3π
C.
D.+2
第20题图
第21题图
21.(2020·苏州)如图,在扇形OAB中,已知∠AOB=90°,OA=,过的中点C作CD⊥OA,CE⊥OB,垂足分别为D,E,则图中阴影部分的面积为( )
A.π-1
B.
-1
C.π-
D.
-
22.(2020·乐山)在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图,将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′.则图中阴影部分面积为( )
A.
B.
C.
D.π
第22题图
第23题图
23.(2020·遂宁)如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=,则图中阴影部分面积为( )
A.4-
B.2-
C.2-π
D.1-
二、填空题
24.在半径为R的圆中,n°的圆心角所对的弧长为______.
25.由组成圆心角的__________和______________围成的图形叫做扇形;半径为R,圆心角为n°的扇形的面积为____________;若已知扇形的半径为R,弧长为l,则扇形的面积为________.
26.(贵港中考)如图,在Rt△ABC中,∠ACB=90°,AB=4,BC=2,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,则图中阴影部分的面积为________.(结果保留π).
第26题图
第27题图
第29题图
第30题图
第31题图
27.如图,一把直角尺的45°角的顶点A落在☉O上,两边分别交☉O于B,C两点.若☉O的半径为2,则的长为
.?
28.若某扇形花坛的面积为6
m2,半径为3
m,则该扇形花坛的弧长为
m.?
29.如图,AB是☉O的直径,弦CD⊥AB于点E,连接BD,∠ABD=60°,CD=2,则的长为
.?
30.如图,在△ABC中,BC=2,∠B=60°,若把线段BC绕着点B旋转,使得点C落在直线AB上的点D处,旋转角度大于0°且小于180°,那么线段BC扫过的面积等于
.(结果保留π)?
31.(天水中考)如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长是
.?
三、解答题
32.如图,A,B,C三点在半径为1的☉O上,四边形ABCO是菱形,求的长.
33.如图,AB是半圆的直径,C,D是的三等分点,☉O的半径为1.
(1)求的长;
(2)求图中阴影部分的面积.
34.如图,AB是☉O的直径,弦CD交AB于点E,∠ACD=60°,∠ADC=50°.
(1)求∠CEB的度数;
(2)若AD=2,求扇形AOC的面积.
35.如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得BD=CB,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
36.如图,AB是☉O的直径,C,D是☉O上的点,OC∥BD交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
37.(2020·郴州)如图,△ABC内接于⊙O,AB是⊙O的直径.直线l与⊙O相切于点A,在l上取一点D使得DA=DC,线段DC,AB的延长线交于点E.
(1)求证:直线DC是⊙O的切线.
(2)若BC=2,∠CAB=30°,求图中阴影部分的面积(结果保留π).
38.如图,在平面直角坐标系中,直线l的函数解析式为y=x,点O1的坐标为(1,0),以点O1为圆心、O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和围成的弓形面积记为S1;以点O2为圆心、O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围成的弓形面积记为S2;以点O3为圆心、O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和围成的弓形面积记为S3;……按此做法进行下去,求S2021.
39.如图,半圆O的直径AB=6,弦CD的长为3,点C,D在上运动,点D在上运动,且不与点A重合,但点C可与点B重合.
(1)当的长为时,求的长;
(2)取CD的中点M,在CD运动的过程中,求点M到AB的距离的最小值.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图,☉O的半径为6,☉O上有三点A,B,C,且∠ACB=30°,则的长等于
(B)
A.π
B.2π
C.3π
D.4π
第1题图
第5题图
第10题图
第11题图
2.(2019·温州)若扇形的圆心角为90°,半径为6,则该扇形的弧长为( C )
A.π
B.2π
C.3π
D.6π
3.有一段长度为2.5π的弧,则此弧所对的圆心角的度数为75°,则这段圆弧所在圆的半径是
(C)
A.3
B.4
C.6
D.12
4.有一条弧的长为2π
cm,半径为2
cm,则这条弧所对的圆心角的度数是
(D)
A.90°
B.120°
C.135°
D.180°
5.如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,AB的长为32
cm,BD的长为14
cm,则的长为
(C)
A.π
cm
B.12π
cm
C.15π
cm
D.36π
cm
6.若扇形的圆心角为90°,半径为6,则该扇形的面积为
(D)
A.
B.3π
C.6π
D.9π
7.如果弧长为4π
cm的扇形面积为16π
cm2,那么该扇形的半径为
(A)
A.8
cm
B.9
cm
C.10
cm
D.11
cm
8.已知一个扇形的半径等于一个圆的半径的2倍,且它的面积等于该已知圆的面积,则这一扇形的圆心角为
(B)
A.60°
B.90°
C.120°
D.150°
9.若钟面上分针的长为1,则从9点到9点15分,分针在钟面上扫过的面积是
(B)
A.π
B.π
C.π
D.π
10.(2020·南充)如图,四个三角形拼成一个风车图形,若AB=2,当风车转动90°,点B运动路径的长度为( A )
A.π
B.2π
C.3π
D.4π
11.(中考·咸宁)如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD,若∠BOD=∠BCD,则的长为( C )
A.π
B.π
C.2π
D.3π
12.(2020·聊城)如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M,连接OC,DB,如果OC∥DB,OC=2,那么图中阴影部分的面积是( B )
A.π
B.2π
C.3π
D.4π
第12题图
第13题图
第14题图
第15题图
13.(2019·宁夏)如图,正六边形ABCDEF的边长为2,分别以点A,D为圆心,以AB,DC为半径作扇形ABF、扇形DCE,则图中阴影部分的面积是( B )
A.6-π
B.6-π
C.12-π
D.12-π
14.如图,AB为☉O的直径,点C在☉O上.若∠OCA=40°,AB=6,则的长为( D )
A.
B.
C.
D.
15.(咸宁中考)如图,☉O的半径为3,四边形ABCD内接于☉O,连接OB,OD.若∠BOD=∠BCD,则的长为( C )
A.π
B.π
C.2π
D.3π
16.如图,正方形ABCD的边长为3,以点A为圆心、2为半径作圆弧,以点D为圆心、3为半径作圆弧.若图中阴影部分的面积分别为S1,S2,则S1-S2的值为( C )
A.9
B.9-π
C.π-9
D.π
第16题图
第17题图
第18题图
第19题图
17.如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与AE交于点H,则的长为
(B)
A.π
B.π
C.π
D.π
18.如图,AB⊥OB,AB=2,OB=4,把∠ABO绕点O顺时针旋转60°得到∠CDO,则AB扫过的面积(图中阴影部分)为
(C)
A.2
B.2π
C.π
D.π
19.边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为
(B)
A.
B.
C.π
D.
20.(2020·淄博)如图,放置在直线l上的扇形OAB,由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径OA=2,∠AOB=45°,则点O所经过的路径的长是( )
A.2π+2
B.3π
C.
D.+2
【点拨】如图所示.
第20题图
第21题图
21.(2020·苏州)如图,在扇形OAB中,已知∠AOB=90°,OA=,过的中点C作CD⊥OA,CE⊥OB,垂足分别为D,E,则图中阴影部分的面积为( )
A.π-1
B.
-1
C.π-
D.
-
【点拨】∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=∠AOB=90°.∴四边形CDOE是矩形.
连接OC.
∵点C是的中点,
∴∠AOC=∠BOC.
又∵OC=OC,
∴△COD≌△COE(AAS).
∴OD=OE.
∴矩形CDOE是正方形.
∵OC=OA=,∴OE=1.
∴S阴影=S扇形OAB-S正方形CDOE=-1×1=-1.
【答案】B
22.(2020·乐山)在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图,将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′.则图中阴影部分面积为( )
A.
B.
C.
D.π
第22题图
第23题图
【点拨】∵∠ABC=90°,∠BAC=30°,BC=1,
∠BAB′=90°,
∴∠CAB′=60°,AC=2BC=2.
∴AB=.
∴S阴影=--×1×=.
【答案】B
23.(2020·遂宁)如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=,则图中阴影部分面积为( )
A.4-
B.2-
C.2-π
D.1-
【点拨】如图,连接OD,过点O作OH⊥AC于点H.
∵∠C=90°,AC=BC,
∴∠B=∠CAB=45°.
∵⊙O与BC相切于点D,
∴OD⊥BC.
∴四边形ODCH为矩形.
∴OH=CD=.
在Rt△OAH中,∠OAH=45°,
∴OA=OH=2.
∴OD=OA=2.
在Rt△OBD中,∠B=45°,
∴∠BOD=45°,BD=OD=2.
∴S阴影=S△OBD-S扇形ODE=×2×2-=2-.
【答案】B
二、填空题
24.在半径为R的圆中,n°的圆心角所对的弧长为______.
【答案】
25.由组成圆心角的__________和______________围成的图形叫做扇形;半径为R,圆心角为n°的扇形的面积为____________;若已知扇形的半径为R,弧长为l,则扇形的面积为________.
【答案】两条半径;圆心角所对的弧;;lR
26.(贵港中考)如图,在Rt△ABC中,∠ACB=90°,AB=4,BC=2,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,则图中阴影部分的面积为________.(结果保留π).
【答案】4π
第26题图
第27题图
第29题图
第30题图
第31题图
27.如图,一把直角尺的45°角的顶点A落在☉O上,两边分别交☉O于B,C两点.若☉O的半径为2,则的长为 π .?
28.若某扇形花坛的面积为6
m2,半径为3
m,则该扇形花坛的弧长为 4 m.?
29.如图,AB是☉O的直径,弦CD⊥AB于点E,连接BD,∠ABD=60°,CD=2,则的长为?π .?
30.如图,在△ABC中,BC=2,∠B=60°,若把线段BC绕着点B旋转,使得点C落在直线AB上的点D处,旋转角度大于0°且小于180°,那么线段BC扫过的面积等于?π .(结果保留π)?
31.(天水中考)如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长是 4π .?
三、解答题
32.如图,A,B,C三点在半径为1的☉O上,四边形ABCO是菱形,求的长.
解:连接OB.
∵四边形OABC是菱形,
∴OA=AB=OB=OC=BC,
∴△AOB,△BOC都是等边三角形,
∴∠AOB=∠BOC=60°,∴∠AOC=120°,
∴.
33.如图,AB是半圆的直径,C,D是的三等分点,☉O的半径为1.
(1)求的长;
(2)求图中阴影部分的面积.
解:(1)∵C,D是的三等分点,∴∠COD=60°,
∴的长l=.
(2)图中阴影部分的面积=.
34.如图,AB是☉O的直径,弦CD交AB于点E,∠ACD=60°,∠ADC=50°.
(1)求∠CEB的度数;
(2)若AD=2,求扇形AOC的面积.
解:(1)连接BC.∵AB是☉O的直径,∴∠ACB=90°.
又∵∠ABC=∠ADC=50°,∴∠BAC=40°,
∴∠CEB=∠ACD+∠BAC=60°+40°=100°.
(2)连接BD,OC,则∠AOC=2∠ADC=100°.
∵∠BAD=∠BCD=30°,∠ADB=90°,AD=2,
∴AB=4,∴AO=2,∴扇形AOC的面积=.
35.如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得BD=CB,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
证明:连接BO.
∵∠ACB=30°,OB=OC,∴∠OBC=∠OCB=30°.
∵DE⊥AC,CB=BD.
∴BE=CD=BC.
∴∠BEC=∠BCE=30°.
∴在△BCE中,∠EBC=180°-∠BEC-∠BCE=120°.
∴∠EBO=∠EBC-∠OBC=120°-30°=90°.
∴BE是⊙O的切线.
(2)当BE=3时,求图中阴影部分的面积.
解:当BE=3时,BC=3.
∵AC为⊙O的直径,∴∠ABC=90°.
又∵∠ACB=30°,∴AB=AC.
∵AB2+BC2=AC2,∴AB=.
∴AC=2.∴AO=.
∴S阴影=S半圆形-SRt△ABC=π×AO2-AB×BC=π×3-××3=π-
.
36.如图,AB是☉O的直径,C,D是☉O上的点,OC∥BD交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=6,∠CBD=30°,求图中阴影部分的面积.
解:(1)∵AB是☉O的直径,∴∠ADB=90°.
∵OC∥BD,O为AB的中点,
∴OE为△ABD的中位线,∴AE=ED.
(2)连接OD.
∵OC∥BD,∠CBD=30°,∴∠OCB=∠CBD=30°.
∵OC=OB,∴∠OBC=∠OCB=30°,
∴∠AOC=∠OCB+∠OBC=60°.
∵∠COD=2∠CBD=60°,∴∠AOD=120°.
由(1)可知∠AEO=90°,
∴∠AOE=60°,∠OAE=30°.
∵AB=6,∴OA=,
∴S阴影=S扇形AOD-S△AOD=.
37.(2020·郴州)如图,△ABC内接于⊙O,AB是⊙O的直径.直线l与⊙O相切于点A,在l上取一点D使得DA=DC,线段DC,AB的延长线交于点E.
(1)求证:直线DC是⊙O的切线.
证明:如图,连接OC.
∵AB是⊙O的直径,直线l与⊙O相切于点A,∴∠DAB=90°.
∵DA=DC,OA=OC,
∴∠DAC=∠DCA,∠OAC=∠OCA.
∴∠DCA+∠OCA=∠DAC+∠OAC,
即∠DCO=∠DAO=90°.
∴OC⊥DC.
∴直线DC是⊙O的切线.
(2)若BC=2,∠CAB=30°,求图中阴影部分的面积(结果保留π).
【思路点拨】连接OC,将阴影部分的面积转化为△OCE与扇形OCB的面积之差.
解:∵∠CAB=30°,
∴∠BOC=2∠CAB=60°.
又∵OC=OB,∴△COB是等边三角形.
∴OC=OB=BC=2.
在Rt△OCE中,∠EOC=60°,
∴∠E=30°.
∴OE=2OC=4.
∴CE=2.
∴S阴影=S△OCE-S扇形OCB=×2×2-=2-.
38.如图,在平面直角坐标系中,直线l的函数解析式为y=x,点O1的坐标为(1,0),以点O1为圆心、O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和围成的弓形面积记为S1;以点O2为圆心、O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围成的弓形面积记为S2;以点O3为圆心、O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和围成的弓形面积记为S3;……按此做法进行下去,求S2021.
解:连接P1O1,P2O2,P3O3,P4O4,…,
∵P1是☉O1上的点,∴P1O1=O1O2.
∵直线l的解析式为y=x,∴∠P1OO1=30°,
∴∠P1O1O2=60°,∴△O1P1O2是等边三角形,
∴△O1P1O2的边长=1,∴△O1P1O2的面积=,
∴S1=π-,
同理S2=π-,S3=π-4,S4=-16π-42,…
∴Sn=π-4n-2,∴S2021=π-42019.
39.如图,半圆O的直径AB=6,弦CD的长为3,点C,D在上运动,点D在上运动,且不与点A重合,但点C可与点B重合.
(1)当的长为时,求的长;
(2)取CD的中点M,在CD运动的过程中,求点M到AB的距离的最小值.
解:(1)连接OD,OC.
∵AB=6,CD=3,
∴OC=OD=AB=CD=3,
∴△CDO是等边三角形,∴∠COD=60°,
∴=π.
∵×6π=3π,
∴.
(2)过点M作ME⊥AB于点E,连接OM.
∵CD=3,∴DM=.
∵△CDO是等边三角形,M为CD的中点,
∴∠OMD=90°,∠DOM=∠COM=30°,
∴在Rt△OMD中,OM=.
∵在Rt△DME中,ME2=OM2-OE2,
∴若ME取最小值,则只需要OE最大即可.
当点C与点B重合时,此时OE最大,如图.
∵∠MOC=30°,OM=,
∴ME=,
即点M到AB的距离的最小值为.
同课章节目录
