人教版八年级数学上册一课一练试题 11.2.2《三角形的外角》 (Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册一课一练试题 11.2.2《三角形的外角》 (Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 120.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 11:06:13 | ||
图片预览



文档简介
11.2.2《三角形的外角》
一、选择题
1.AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
A.25°
B.60°
C.85°
D.95°
2.(2020春?黑河期中)以下判断正确的是( )
A.三角形的一个外角等于两个内角的和
B.三角形的外角大于任何一个内角
C.一个三角形中,至少有一个角大于或等于60°
D.三角形的外角是内角的邻补角
3.如图,已知∠ACD=130°,∠B=20°,则∠A的度数是( )
A.110°
B.30°
C.150°
D.90°
4.如图,△ABC中,点D在BC延长线上,则下列结论一定成立的是( )
A.∠1=∠A+∠B
B.∠1=∠2+∠A
C.∠1=∠2+∠B
D.∠2=∠A+∠B
5.如图,在△ABC中,∠A=78°,∠ACD是△ABC的一个外角,∠EBC∠ABC,∠ECD∠ACD,则∠E为( )
A.22°
B.26°
C.28°
D.30°
6.如图,∠1,∠2,∠3,∠4恒满足关系式是( )
A.∠1+∠2=∠3+∠4
B.∠1+∠2=∠4﹣∠3
C.∠1+∠4=∠2+∠3
D.∠1+∠4=∠2﹣∠3
7.如图,在△ABC中,∠B=45°,∠C=30°,延长线段BA至点E,则∠EAC的度数为( )
A.105°
B.75°
C.70°
D.60°
8.在△ABC,∠A,∠C与∠B的外角度数如图所示,则x的值是( )
A.80
B.70
C.65
D.60
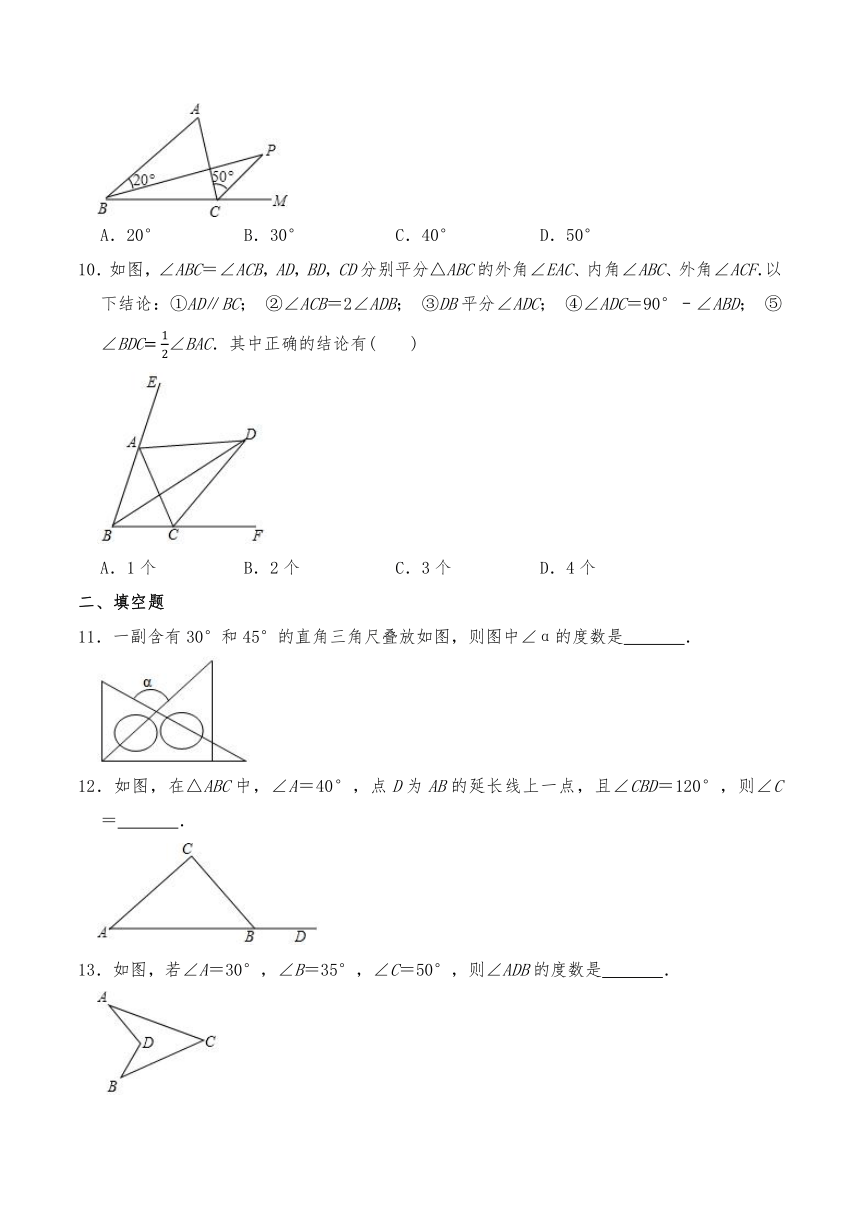
9.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线.如果∠ABP=20°,∠ACP=50°,则∠P=( )
A.20°
B.30°
C.40°
D.50°
10.如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;
②∠ACB=2∠ADB;
③DB平分∠ADC;
④∠ADC=90°﹣∠ABD;
⑤∠BDC∠BAC.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
二、填空题
11.一副含有30°和45°的直角三角尺叠放如图,则图中∠α的度数是
.
12.如图,在△ABC中,∠A=40°,点D为AB的延长线上一点,且∠CBD=120°,则∠C=
.
13.如图,若∠A=30°,∠B=35°,∠C=50°,则∠ADB的度数是
.
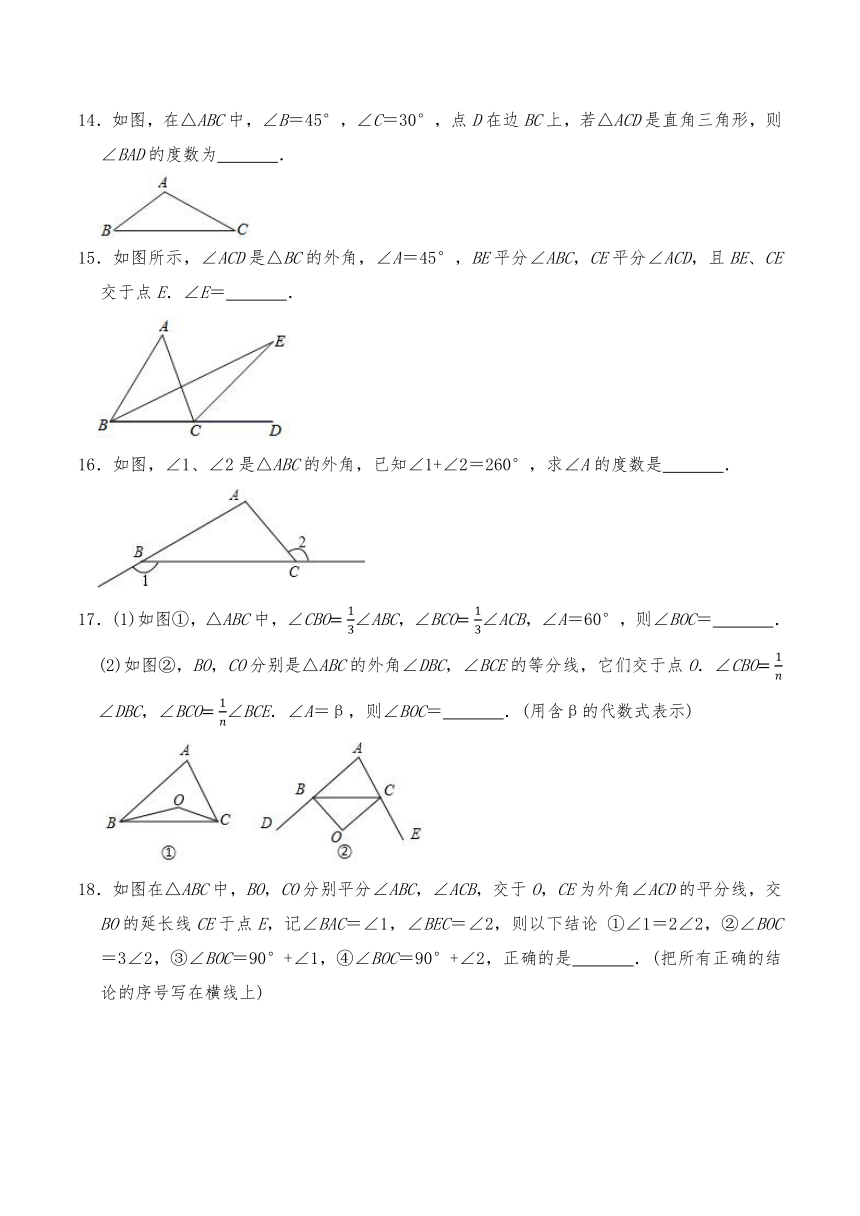
14.如图,在△ABC中,∠B=45°,∠C=30°,点D在边BC上,若△ACD是直角三角形,则∠BAD的度数为
.
15.如图所示,∠ACD是△BC的外角,∠A=45°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.∠E=
.
16.如图,∠1、∠2是△ABC的外角,已知∠1+∠2=260°,求∠A的度数是
.
17.(1)如图①,△ABC中,∠CBO∠ABC,∠BCO∠ACB,∠A=60°,则∠BOC=
.
(2)如图②,BO,CO分别是△ABC的外角∠DBC,∠BCE的等分线,它们交于点O.∠CBO∠DBC,∠BCO∠BCE.∠A=β,则∠BOC=
.(用含β的代数式表示)
18.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,交BO的延长线CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论
①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2,正确的是
.(把所有正确的结论的序号写在横线上)
三、解答题
19.用两种方法证明“三角形的外角和等于360°”.如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵∠BAE、∠CBF、∠ACD是△ABC的三个外角.
∴
.
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),
∵
.
∴∠BAE+∠CBF+∠ACD=360°
请把证法1补充完整,并用不同的方法完成证法2.
20.已知:如图,△ABC的两个外角的平分线交于点P,如果∠A=40°,求∠BPC的度数.
21.如图,∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E,∠ABC=∠ACE.
(1)求证:AB∥CE;
(2)猜想:若∠A=50°,求∠E的度数.
22.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=35°,∠E=25°,求∠BAC的度数;
(2)请你写出∠BAC、∠B、∠E三个角之间存在的等量关系,并写出证明过程.
23.如图,∠A=37°,∠B=28°,∠ADB=148°,求∠C的度数.
24.某校八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.
(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC=
;
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC与∠A的数量关系,并证明.
答案
一、选择题
1.D.2.C.3.A.4.A.5.B.6.D.7.B.8.B.9.B.10.D.
二、填空题
11.105°.
12.80°.
13.115°.
14.45°或15°.
15.22.5°
16.80°.
17.150°;.
18.①④.
三、解答题
19.证明:证法1:∵∠BAE、∠CBF、∠ACD是△ABC的三个外角.
∴∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2.
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),
∵∠1+∠2+∠3=180°.
∴∠BAE+∠CBF+∠ACD=360°;
证法2:∵平角等于180°,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
20.∵∠A=40°,
∴∠ABC+∠ACB=180°﹣40°=140°,
∴∠EBC+∠FCB=360°﹣140°=220°,
∵BP、CP是△ABC的外角平分线,
∴∠PBC∠EBC,∠PCB∠FCB,
∴∠PBC+∠PCB(∠EBC+∠FCB)=110°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=70°.
21.(1)证明:∵CE平分∠ACD,
∴∠ECD=∠ACE,
∵∠ABC=∠ACE
∴∠ABC=∠ECD,
∴AB∥CE;
(2)解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠ABC+∠A,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠E=∠ECD﹣∠EBC∠ACD∠ABC∠A=25°.
22.(1)∵∠ECD=∠B+∠E,∠B=35°,∠E=25°,
∴∠ECD=60°,
∵EC平分∠ACD,
∴∠ACE=∠ECD=60°,
∴∠BAC=∠ACE+∠E=60°+25°=85°.
(2)结论:∠BAC=∠B+2∠E.
理由:∵∠BAC=∠ACE+∠E,
∠ECD=∠ACE=∠B+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
23.连接CD并延长点E,
∵∠ACD=∠ADE﹣∠A=∠ADE﹣37°,
∴∠A=37°,∠ADE=∠A+∠ACD,
同理可得:∠BCD=∠BDE﹣28°,
∵∠ACB=∠ACD+∠BCD,
∴∠ADB=148°,
∠ACB=∠ADB﹣∠A﹣∠B,
=148°﹣37°﹣28°
=83°.
24.(1)∵BP、CP分别平分∠ABC和∠ACB,
∴∠PBC∠ABC,∠PCB∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(∠ABC∠ACB),
=180°(∠ABC+∠ACB),
=180°(180°﹣∠A),
=180°﹣90°∠A,
=90°+32°=122°,
故答案为:122°;
(2)∵CE和BE分别是∠ACB和∠ABD的角平分线,
∴∠1∠ACB,∠2∠ABD,
又∵∠ABD是△ABC的一外角,
∴∠ABD=∠A+∠ACB,
∴∠2(∠A+∠ABC)∠A+∠1,
∵∠2是△BEC的一外角,
∴∠BEC=∠2﹣∠1∠A+∠1﹣∠1∠A;
(3)∠QBC(∠A+∠ACB),∠QCB(∠A+∠ABC),
∠BQC=180°﹣∠QBC﹣∠QCB,
=180°(∠A+∠ACB)(∠A+∠ABC),
=180°∠A(∠A+∠ABC+∠ACB),
结论∠BQC=90°∠A.
一、选择题
1.AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD=( )
A.25°
B.60°
C.85°
D.95°
2.(2020春?黑河期中)以下判断正确的是( )
A.三角形的一个外角等于两个内角的和
B.三角形的外角大于任何一个内角
C.一个三角形中,至少有一个角大于或等于60°
D.三角形的外角是内角的邻补角
3.如图,已知∠ACD=130°,∠B=20°,则∠A的度数是( )
A.110°
B.30°
C.150°
D.90°
4.如图,△ABC中,点D在BC延长线上,则下列结论一定成立的是( )
A.∠1=∠A+∠B
B.∠1=∠2+∠A
C.∠1=∠2+∠B
D.∠2=∠A+∠B
5.如图,在△ABC中,∠A=78°,∠ACD是△ABC的一个外角,∠EBC∠ABC,∠ECD∠ACD,则∠E为( )
A.22°
B.26°
C.28°
D.30°
6.如图,∠1,∠2,∠3,∠4恒满足关系式是( )
A.∠1+∠2=∠3+∠4
B.∠1+∠2=∠4﹣∠3
C.∠1+∠4=∠2+∠3
D.∠1+∠4=∠2﹣∠3
7.如图,在△ABC中,∠B=45°,∠C=30°,延长线段BA至点E,则∠EAC的度数为( )
A.105°
B.75°
C.70°
D.60°
8.在△ABC,∠A,∠C与∠B的外角度数如图所示,则x的值是( )
A.80
B.70
C.65
D.60
9.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线.如果∠ABP=20°,∠ACP=50°,则∠P=( )
A.20°
B.30°
C.40°
D.50°
10.如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;
②∠ACB=2∠ADB;
③DB平分∠ADC;
④∠ADC=90°﹣∠ABD;
⑤∠BDC∠BAC.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
二、填空题
11.一副含有30°和45°的直角三角尺叠放如图,则图中∠α的度数是
.
12.如图,在△ABC中,∠A=40°,点D为AB的延长线上一点,且∠CBD=120°,则∠C=
.
13.如图,若∠A=30°,∠B=35°,∠C=50°,则∠ADB的度数是
.
14.如图,在△ABC中,∠B=45°,∠C=30°,点D在边BC上,若△ACD是直角三角形,则∠BAD的度数为
.
15.如图所示,∠ACD是△BC的外角,∠A=45°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.∠E=
.
16.如图,∠1、∠2是△ABC的外角,已知∠1+∠2=260°,求∠A的度数是
.
17.(1)如图①,△ABC中,∠CBO∠ABC,∠BCO∠ACB,∠A=60°,则∠BOC=
.
(2)如图②,BO,CO分别是△ABC的外角∠DBC,∠BCE的等分线,它们交于点O.∠CBO∠DBC,∠BCO∠BCE.∠A=β,则∠BOC=
.(用含β的代数式表示)
18.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,交BO的延长线CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论
①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2,正确的是
.(把所有正确的结论的序号写在横线上)
三、解答题
19.用两种方法证明“三角形的外角和等于360°”.如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵∠BAE、∠CBF、∠ACD是△ABC的三个外角.
∴
.
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),
∵
.
∴∠BAE+∠CBF+∠ACD=360°
请把证法1补充完整,并用不同的方法完成证法2.
20.已知:如图,△ABC的两个外角的平分线交于点P,如果∠A=40°,求∠BPC的度数.
21.如图,∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E,∠ABC=∠ACE.
(1)求证:AB∥CE;
(2)猜想:若∠A=50°,求∠E的度数.
22.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=35°,∠E=25°,求∠BAC的度数;
(2)请你写出∠BAC、∠B、∠E三个角之间存在的等量关系,并写出证明过程.
23.如图,∠A=37°,∠B=28°,∠ADB=148°,求∠C的度数.
24.某校八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.
(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC=
;
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC与∠A的数量关系,并证明.
答案
一、选择题
1.D.2.C.3.A.4.A.5.B.6.D.7.B.8.B.9.B.10.D.
二、填空题
11.105°.
12.80°.
13.115°.
14.45°或15°.
15.22.5°
16.80°.
17.150°;.
18.①④.
三、解答题
19.证明:证法1:∵∠BAE、∠CBF、∠ACD是△ABC的三个外角.
∴∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2.
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),
∵∠1+∠2+∠3=180°.
∴∠BAE+∠CBF+∠ACD=360°;
证法2:∵平角等于180°,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
20.∵∠A=40°,
∴∠ABC+∠ACB=180°﹣40°=140°,
∴∠EBC+∠FCB=360°﹣140°=220°,
∵BP、CP是△ABC的外角平分线,
∴∠PBC∠EBC,∠PCB∠FCB,
∴∠PBC+∠PCB(∠EBC+∠FCB)=110°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=70°.
21.(1)证明:∵CE平分∠ACD,
∴∠ECD=∠ACE,
∵∠ABC=∠ACE
∴∠ABC=∠ECD,
∴AB∥CE;
(2)解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠ABC+∠A,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠E=∠ECD﹣∠EBC∠ACD∠ABC∠A=25°.
22.(1)∵∠ECD=∠B+∠E,∠B=35°,∠E=25°,
∴∠ECD=60°,
∵EC平分∠ACD,
∴∠ACE=∠ECD=60°,
∴∠BAC=∠ACE+∠E=60°+25°=85°.
(2)结论:∠BAC=∠B+2∠E.
理由:∵∠BAC=∠ACE+∠E,
∠ECD=∠ACE=∠B+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
23.连接CD并延长点E,
∵∠ACD=∠ADE﹣∠A=∠ADE﹣37°,
∴∠A=37°,∠ADE=∠A+∠ACD,
同理可得:∠BCD=∠BDE﹣28°,
∵∠ACB=∠ACD+∠BCD,
∴∠ADB=148°,
∠ACB=∠ADB﹣∠A﹣∠B,
=148°﹣37°﹣28°
=83°.
24.(1)∵BP、CP分别平分∠ABC和∠ACB,
∴∠PBC∠ABC,∠PCB∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(∠ABC∠ACB),
=180°(∠ABC+∠ACB),
=180°(180°﹣∠A),
=180°﹣90°∠A,
=90°+32°=122°,
故答案为:122°;
(2)∵CE和BE分别是∠ACB和∠ABD的角平分线,
∴∠1∠ACB,∠2∠ABD,
又∵∠ABD是△ABC的一外角,
∴∠ABD=∠A+∠ACB,
∴∠2(∠A+∠ABC)∠A+∠1,
∵∠2是△BEC的一外角,
∴∠BEC=∠2﹣∠1∠A+∠1﹣∠1∠A;
(3)∠QBC(∠A+∠ACB),∠QCB(∠A+∠ABC),
∠BQC=180°﹣∠QBC﹣∠QCB,
=180°(∠A+∠ACB)(∠A+∠ABC),
=180°∠A(∠A+∠ABC+∠ACB),
结论∠BQC=90°∠A.
