人教版八年级数学上册一课一练试题 11.2.1《三角形的内角》(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册一课一练试题 11.2.1《三角形的内角》(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 91.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 11:07:46 | ||
图片预览




文档简介
11.2.1《三角形的内角》
一、选择题
1.△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC的形状是( )
A.直角三角形
B.等腰三角形
C.锐角三角形
D.钝角三角形
2.将一副三角板如图放置,作CF∥AB,则∠EFC的度数是( )
A.90°
B.100°
C.105°
D.110°
3.下列条件能说明△ABC是直角三角形的是( )
A.∠A=∠B=2∠C
B.∠A=∠B+∠C
C.∠A:∠B:∠C=2:3:4
D.∠A=40°,∠B=55°
4.如图,△ABC中,∠A=75°,∠B=65°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为( )
A.40°
B.45°
C.50°
D.60°
5.如图,在△ABC中,∠ABC=75°,∠ABD=∠BCD,则∠BDC的度数是( )
A.115°
B.110°
C.105°
D.100°
6.下列条件:①∠A﹣∠B=∠C;
②∠A:∠B:∠C=2:3:5;
③∠A∠B∠C;④∠A=∠B=2∠C;⑤∠A=∠B∠C,其中能确定△ABC为直角三角形的条件有( )
A.2个
B.3个
C.4个
D.5个
7.在△ABC中,∠C=40°,∠B=4∠A,则∠A为( )度.
A.30
B.28
C.26
D.40
8.如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在△ABC外的点C′处,若∠1=20°,则∠2的度数为( )
A.80°
B.90°
C.100°
D.110°
9.如图,在△ABC中,∠A=α,∠B=∠C,点D,E,F分别在BC,AB,AC上,且∠EDF=∠B,若∠2=2∠1,则∠EDB的度数为( )
A.120°﹣a
B.60°a
C.90°a
D.45°a
10.如图,在△ABC中,∠A=40°,高BE、CF交于点O,则∠BOC为( )
A.40°
B.110°
C.130°
D.140°
二、填空题
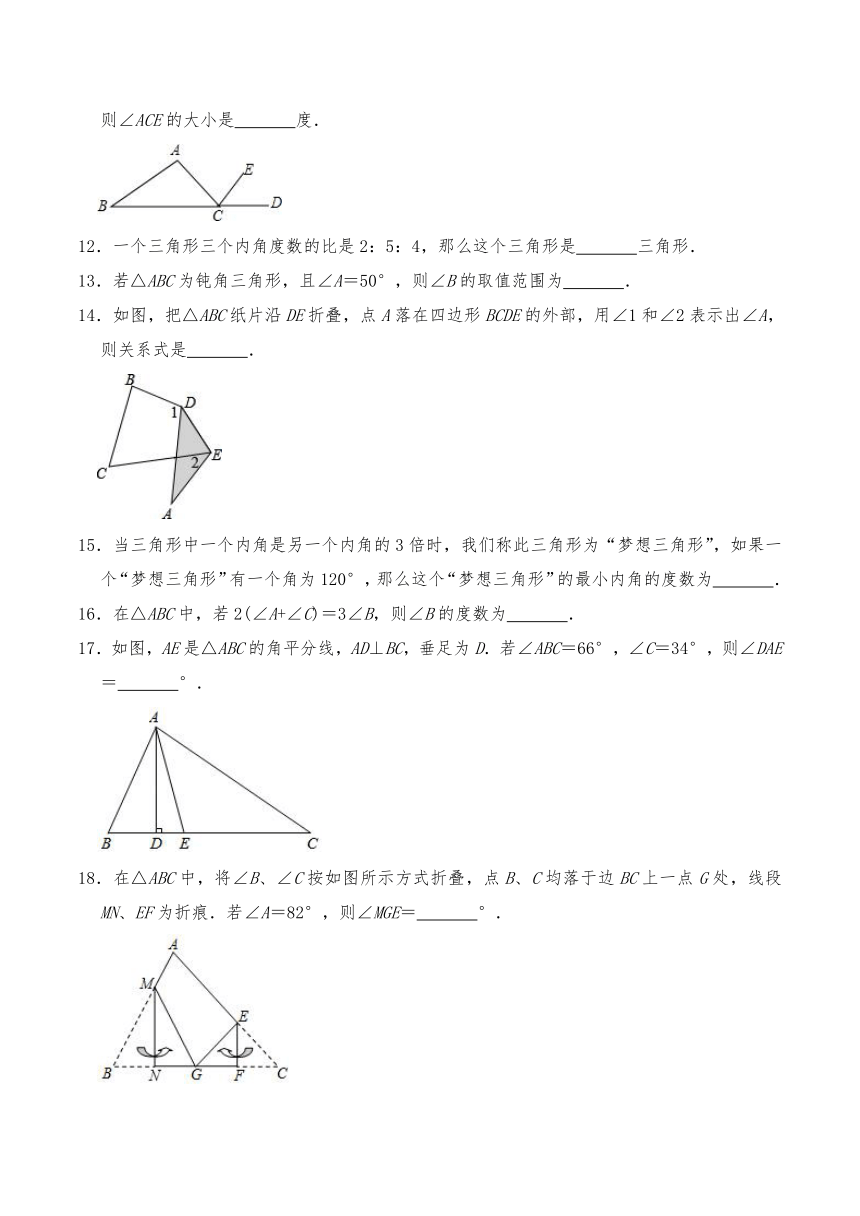
11.如图,点D在三角形ABC的边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=20°,则∠ACE的大小是
度.
12.一个三角形三个内角度数的比是2:5:4,那么这个三角形是
三角形.
13.若△ABC为钝角三角形,且∠A=50°,则∠B的取值范围为
.
14.如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE的外部,用∠1和∠2表示出∠A,则关系式是
.
15.当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”,如果一个“梦想三角形”有一个角为120°,那么这个“梦想三角形”的最小内角的度数为
.
16.在△ABC中,若2(∠A+∠C)=3∠B,则∠B的度数为
.
17.如图,AE是△ABC的角平分线,AD⊥BC,垂足为D.若∠ABC=66°,∠C=34°,则∠DAE=
°.
18.在△ABC中,将∠B、∠C按如图所示方式折叠,点B、C均落于边BC上一点G处,线段MN、EF为折痕.若∠A=82°,则∠MGE=
°.
三、解答题
19.如图,已知,在△ABC中,∠C=∠ABC,BE⊥AC,∠DBE=60°,求∠C的度数.
20.如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=50°.
(1)求∠DAE的度数;
(2)试写出∠DAE与∠C、∠B之间的数量关系(不必说明理由).
21.如图:有一张直角三角形纸片ABC,∠ACB=90°,∠A=50°,将其沿CD折叠,使点A落在边CB上的点A′处,求∠A′DB的度数.
22.如图,在△ABC中,点D在BC上,∠ADB=∠BAC,BE平分∠ABC,过点E作EF∥AD,交BC于点F.
(1)求证:∠BAD=∠C;
(2)若∠C=20°,∠BAC=110°,求∠BEF的度数.
23.如图1,AD、BC交于点O,得到的数学基本图形我们称之为‘8’字形ABCD.
(1)试说明:∠A+∠B=∠C+∠D;
(2)如图2,∠ABC和∠ADC的平分线相交于E,尝试用(1)中的数学基本图形和结论,猜想∠E与∠A、∠C之间的数量关系并说明理由.
24.已知(如图1)在△ABC中,∠B>∠C,AD平分∠BAC,点E在AD的延长线上,过点E作EF⊥BC于点F,设∠B=α,∠C=β.
(1)当α=80°,β=30°时,求∠E的度数;
(2)试问∠E与∠B,∠C之间存在着怎样的数量关系,试用α、β表示∠E,并说明理由;
(3)若∠EFB与∠BAE平分线交于点P(如图2),当点E在AD延长线上运动时,∠P是否发生变化,若不变,请用α、β表示∠P;若变化,请说明理由.
答案
一、选择题
1.A.2.C.3.B.4.D.5.C.6.C.7.B.8.C.9.B.10.D.
二、填空题
11.50.
12.锐角.
13.130°>∠B>90°或0°<∠B<40°.
14.2∠A=∠1﹣∠2.
15.20°或15°.
16.72°
17.16°.
18.82°,
三、解答题
19.∵BE⊥AC,
∴∠AEB=90°,
∵∠DBE=60°,
∴∠A=90°﹣60°=30°,
∴∠C=∠ABC(180°﹣30°)=75°.
20.(1)∵AD是BC边上的高,
∴∠ADE=90°.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣∠B﹣∠C=100°.
∵AE是∠BAC平分线,
∴∠BAE∠BAC=50°,
∴∠AED=∠B+∠BAE=30°+50°=80°.
∵∠ADE+∠AED+∠DAE=180°,
∴∠DAE=180°﹣∠ADE﹣∠AED=180°﹣90°﹣80°=10°.
(2)∠DAE(∠C﹣∠B),理由如下:
∵AD是BC边上的高,
∴∠ADE=90°.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣∠B﹣∠C.
∵AE是∠BAC平分线,
∴∠BAE∠BAC=90°(∠B+∠C),
∴∠AED=∠B+∠BAE=90°(∠B﹣∠C).
∵∠ADE+∠AED+∠DAE=180°,
∴∠DAE=180°﹣∠ADE﹣∠AED=180°﹣90°﹣[90°(∠B﹣∠C)](∠C﹣∠B).
21.由折叠可得,∠CA'D=∠A=50°,
∵∠ACB=90°,∠A=50°,
∴∠B=40°,
∵∠B+∠A'DB=∠CA'D,
∴∠A'DB=50°﹣40°=10°.
22.(1)证明:∵∠ABC+∠BAC+∠C=180°,∠ABC+∠BDA+∠BAD=180°,∠BDA=∠BAC,
∴∠BAD=∠C.
(2)解:∵∠C=20°,∠BAC=110°,
∴∠ABC=180°﹣20°﹣110°=50°,
∵BE平分∠ABC,
∴∠EBF∠ABC=25°,
∵∠BDA=∠BAC=110°,
∴∠BHD=180°﹣∠HBD﹣∠BDA=180°﹣25°﹣110°=45°,
∵AD∥EF,
∴∠BEF=∠BHD=45°.
23.(1)证明:∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
又∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)解:结论:2∠E=∠A+∠C.
理由:∵∠ABC和∠ADC的平分线相交于E,
∴可以假设∠ABE=∠EBC=x,∠ADE=∠EDC=y,
∵∠A+x=∠E+y,∠C+y=∠E+x,
∴∠A+∠C=∠E+∠E,
∴2∠E=∠A+∠C,
24.(1)∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵AD平分∠BAC,
∴∠BADBAC=35°,
∴∠EDF=∠ADB=180°﹣35°﹣80°=65°,
∵EF⊥BC,
∴∠EFD=90°,
∴∠E=90°﹣65°=25°;
(2)∵∠EDF=∠C+∠CAD,∠CAD∠BAC(180°﹣α﹣β),
∴∠EDF=∠C+90°αβ=90°(α﹣β),
∵∠EFD=90°,
∴∠DEF(α﹣β);
(3)设AP与BC交于G,
∵AD平分∠BAC,
∴∠BADBAC(180°﹣α﹣β),
∵AP平分∠BAE,
∴∠BAPBAD(180°﹣α﹣β),
∴∠PGF=∠AGB=180°﹣∠B﹣∠BAP=180°﹣α(180°﹣α﹣β)=135°αβ,
∵PF平分∠EFB,
∴∠PFB=45°,
∴∠P=180°﹣∠PFB﹣∠PGF=180°﹣45°﹣(135°αβ)αβ,
故∠P不会发生变化.
一、选择题
1.△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC的形状是( )
A.直角三角形
B.等腰三角形
C.锐角三角形
D.钝角三角形
2.将一副三角板如图放置,作CF∥AB,则∠EFC的度数是( )
A.90°
B.100°
C.105°
D.110°
3.下列条件能说明△ABC是直角三角形的是( )
A.∠A=∠B=2∠C
B.∠A=∠B+∠C
C.∠A:∠B:∠C=2:3:4
D.∠A=40°,∠B=55°
4.如图,△ABC中,∠A=75°,∠B=65°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为( )
A.40°
B.45°
C.50°
D.60°
5.如图,在△ABC中,∠ABC=75°,∠ABD=∠BCD,则∠BDC的度数是( )
A.115°
B.110°
C.105°
D.100°
6.下列条件:①∠A﹣∠B=∠C;
②∠A:∠B:∠C=2:3:5;
③∠A∠B∠C;④∠A=∠B=2∠C;⑤∠A=∠B∠C,其中能确定△ABC为直角三角形的条件有( )
A.2个
B.3个
C.4个
D.5个
7.在△ABC中,∠C=40°,∠B=4∠A,则∠A为( )度.
A.30
B.28
C.26
D.40
8.如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在△ABC外的点C′处,若∠1=20°,则∠2的度数为( )
A.80°
B.90°
C.100°
D.110°
9.如图,在△ABC中,∠A=α,∠B=∠C,点D,E,F分别在BC,AB,AC上,且∠EDF=∠B,若∠2=2∠1,则∠EDB的度数为( )
A.120°﹣a
B.60°a
C.90°a
D.45°a
10.如图,在△ABC中,∠A=40°,高BE、CF交于点O,则∠BOC为( )
A.40°
B.110°
C.130°
D.140°
二、填空题
11.如图,点D在三角形ABC的边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=20°,则∠ACE的大小是
度.
12.一个三角形三个内角度数的比是2:5:4,那么这个三角形是
三角形.
13.若△ABC为钝角三角形,且∠A=50°,则∠B的取值范围为
.
14.如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE的外部,用∠1和∠2表示出∠A,则关系式是
.
15.当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”,如果一个“梦想三角形”有一个角为120°,那么这个“梦想三角形”的最小内角的度数为
.
16.在△ABC中,若2(∠A+∠C)=3∠B,则∠B的度数为
.
17.如图,AE是△ABC的角平分线,AD⊥BC,垂足为D.若∠ABC=66°,∠C=34°,则∠DAE=
°.
18.在△ABC中,将∠B、∠C按如图所示方式折叠,点B、C均落于边BC上一点G处,线段MN、EF为折痕.若∠A=82°,则∠MGE=
°.
三、解答题
19.如图,已知,在△ABC中,∠C=∠ABC,BE⊥AC,∠DBE=60°,求∠C的度数.
20.如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=50°.
(1)求∠DAE的度数;
(2)试写出∠DAE与∠C、∠B之间的数量关系(不必说明理由).
21.如图:有一张直角三角形纸片ABC,∠ACB=90°,∠A=50°,将其沿CD折叠,使点A落在边CB上的点A′处,求∠A′DB的度数.
22.如图,在△ABC中,点D在BC上,∠ADB=∠BAC,BE平分∠ABC,过点E作EF∥AD,交BC于点F.
(1)求证:∠BAD=∠C;
(2)若∠C=20°,∠BAC=110°,求∠BEF的度数.
23.如图1,AD、BC交于点O,得到的数学基本图形我们称之为‘8’字形ABCD.
(1)试说明:∠A+∠B=∠C+∠D;
(2)如图2,∠ABC和∠ADC的平分线相交于E,尝试用(1)中的数学基本图形和结论,猜想∠E与∠A、∠C之间的数量关系并说明理由.
24.已知(如图1)在△ABC中,∠B>∠C,AD平分∠BAC,点E在AD的延长线上,过点E作EF⊥BC于点F,设∠B=α,∠C=β.
(1)当α=80°,β=30°时,求∠E的度数;
(2)试问∠E与∠B,∠C之间存在着怎样的数量关系,试用α、β表示∠E,并说明理由;
(3)若∠EFB与∠BAE平分线交于点P(如图2),当点E在AD延长线上运动时,∠P是否发生变化,若不变,请用α、β表示∠P;若变化,请说明理由.
答案
一、选择题
1.A.2.C.3.B.4.D.5.C.6.C.7.B.8.C.9.B.10.D.
二、填空题
11.50.
12.锐角.
13.130°>∠B>90°或0°<∠B<40°.
14.2∠A=∠1﹣∠2.
15.20°或15°.
16.72°
17.16°.
18.82°,
三、解答题
19.∵BE⊥AC,
∴∠AEB=90°,
∵∠DBE=60°,
∴∠A=90°﹣60°=30°,
∴∠C=∠ABC(180°﹣30°)=75°.
20.(1)∵AD是BC边上的高,
∴∠ADE=90°.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣∠B﹣∠C=100°.
∵AE是∠BAC平分线,
∴∠BAE∠BAC=50°,
∴∠AED=∠B+∠BAE=30°+50°=80°.
∵∠ADE+∠AED+∠DAE=180°,
∴∠DAE=180°﹣∠ADE﹣∠AED=180°﹣90°﹣80°=10°.
(2)∠DAE(∠C﹣∠B),理由如下:
∵AD是BC边上的高,
∴∠ADE=90°.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣∠B﹣∠C.
∵AE是∠BAC平分线,
∴∠BAE∠BAC=90°(∠B+∠C),
∴∠AED=∠B+∠BAE=90°(∠B﹣∠C).
∵∠ADE+∠AED+∠DAE=180°,
∴∠DAE=180°﹣∠ADE﹣∠AED=180°﹣90°﹣[90°(∠B﹣∠C)](∠C﹣∠B).
21.由折叠可得,∠CA'D=∠A=50°,
∵∠ACB=90°,∠A=50°,
∴∠B=40°,
∵∠B+∠A'DB=∠CA'D,
∴∠A'DB=50°﹣40°=10°.
22.(1)证明:∵∠ABC+∠BAC+∠C=180°,∠ABC+∠BDA+∠BAD=180°,∠BDA=∠BAC,
∴∠BAD=∠C.
(2)解:∵∠C=20°,∠BAC=110°,
∴∠ABC=180°﹣20°﹣110°=50°,
∵BE平分∠ABC,
∴∠EBF∠ABC=25°,
∵∠BDA=∠BAC=110°,
∴∠BHD=180°﹣∠HBD﹣∠BDA=180°﹣25°﹣110°=45°,
∵AD∥EF,
∴∠BEF=∠BHD=45°.
23.(1)证明:∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
又∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)解:结论:2∠E=∠A+∠C.
理由:∵∠ABC和∠ADC的平分线相交于E,
∴可以假设∠ABE=∠EBC=x,∠ADE=∠EDC=y,
∵∠A+x=∠E+y,∠C+y=∠E+x,
∴∠A+∠C=∠E+∠E,
∴2∠E=∠A+∠C,
24.(1)∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵AD平分∠BAC,
∴∠BADBAC=35°,
∴∠EDF=∠ADB=180°﹣35°﹣80°=65°,
∵EF⊥BC,
∴∠EFD=90°,
∴∠E=90°﹣65°=25°;
(2)∵∠EDF=∠C+∠CAD,∠CAD∠BAC(180°﹣α﹣β),
∴∠EDF=∠C+90°αβ=90°(α﹣β),
∵∠EFD=90°,
∴∠DEF(α﹣β);
(3)设AP与BC交于G,
∵AD平分∠BAC,
∴∠BADBAC(180°﹣α﹣β),
∵AP平分∠BAE,
∴∠BAPBAD(180°﹣α﹣β),
∴∠PGF=∠AGB=180°﹣∠B﹣∠BAP=180°﹣α(180°﹣α﹣β)=135°αβ,
∵PF平分∠EFB,
∴∠PFB=45°,
∴∠P=180°﹣∠PFB﹣∠PGF=180°﹣45°﹣(135°αβ)αβ,
故∠P不会发生变化.
