人教版八年级数学上册一课一练试题 11.3《多边形及其内角和》(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册一课一练试题 11.3《多边形及其内角和》(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 115.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 11:12:06 | ||
图片预览


文档简介
11.3《多边形及其内角和》
一、选择题
1.内角和为720°的多边形是( )
A.
B.
C.
D.
2.如果一个正多边形的内角和是外角和的3倍,那么这个正多边形的边数为( )
A.5
B.6
C.7
D.8
3.设四边形的内角和等于a,五边形的内角和等于b,则a与b的关系是( )
A.a>b
B.a=b
C.a=b+180°
D.b=a+180°
4.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为( )
A.100米
B.80米
C.60米
D.40米
5.若某多边形的边数增加1,则这个多边形的外角和( )
A.增加180°
B.增加360°
C.减少180°
D.不变
6.若正多边形的一个外角是36°,则该正多边形的内角和为( )
A.360°
B.720°
C.900°
D.1440°
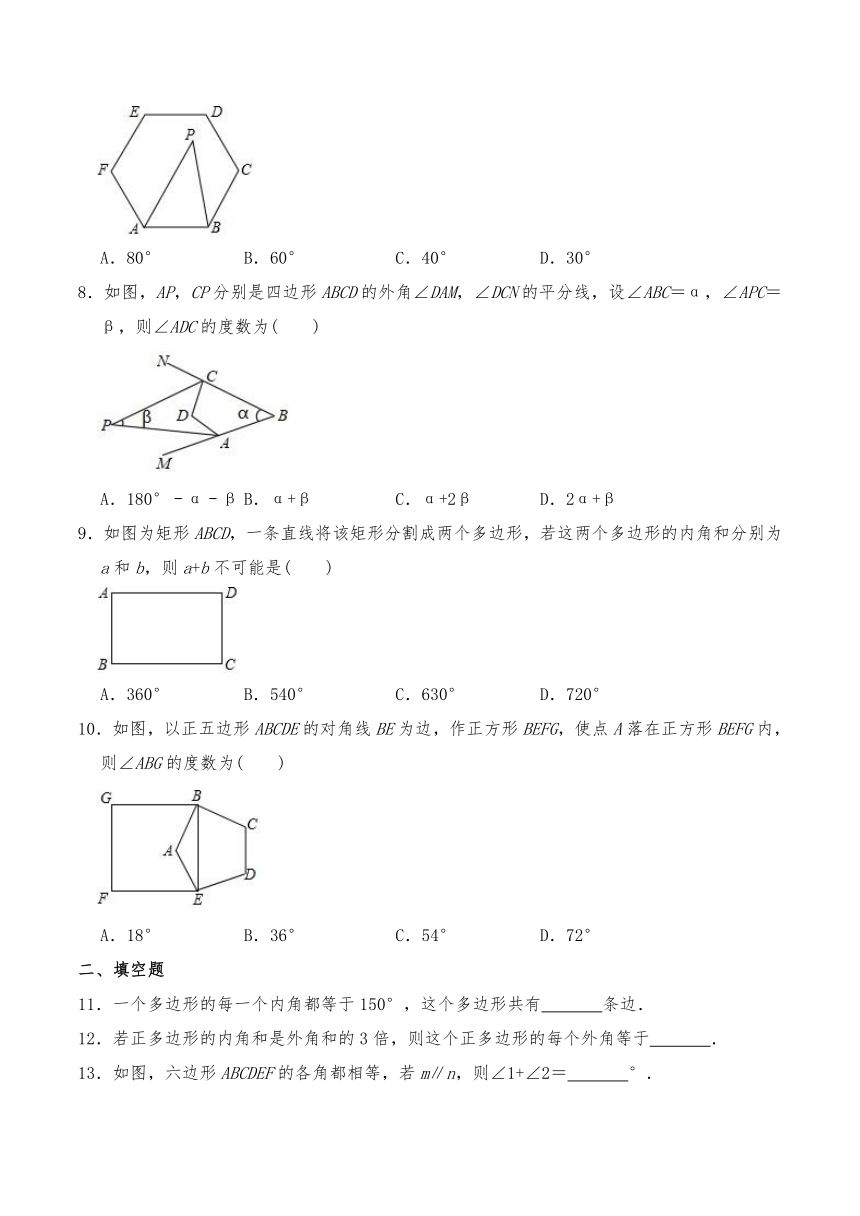
7.如图,过正六边形ABCDEF的顶点B作一条射线与其内角∠BAF的角平分线相交于点P,且∠APB=40°,则∠CBP的度数为( )
A.80°
B.60°
C.40°
D.30°
8.如图,AP,CP分别是四边形ABCD的外角∠DAM,∠DCN的平分线,设∠ABC=α,∠APC=β,则∠ADC的度数为( )
A.180°﹣α﹣β
B.α+β
C.α+2β
D.2α+β
9.如图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360°
B.540°
C.630°
D.720°
10.如图,以正五边形ABCDE的对角线BE为边,作正方形BEFG,使点A落在正方形BEFG内,则∠ABG的度数为( )
A.18°
B.36°
C.54°
D.72°
二、填空题
11.一个多边形的每一个内角都等于150°,这个多边形共有
条边.
12.若正多边形的内角和是外角和的3倍,则这个正多边形的每个外角等于
.
13.如图,六边形ABCDEF的各角都相等,若m∥n,则∠1+∠2=
°.
14.如图,已知∠B=30°,则∠A+∠D+∠C+∠G=
°.
15.已知正n边形的一个内角为135°,则n的值是
.
16.如图,将四边形纸片ABCD沿MN折叠,点A、D分别落在A1、D1处,若∠1+∠2=145°,则∠B+∠C=
°.
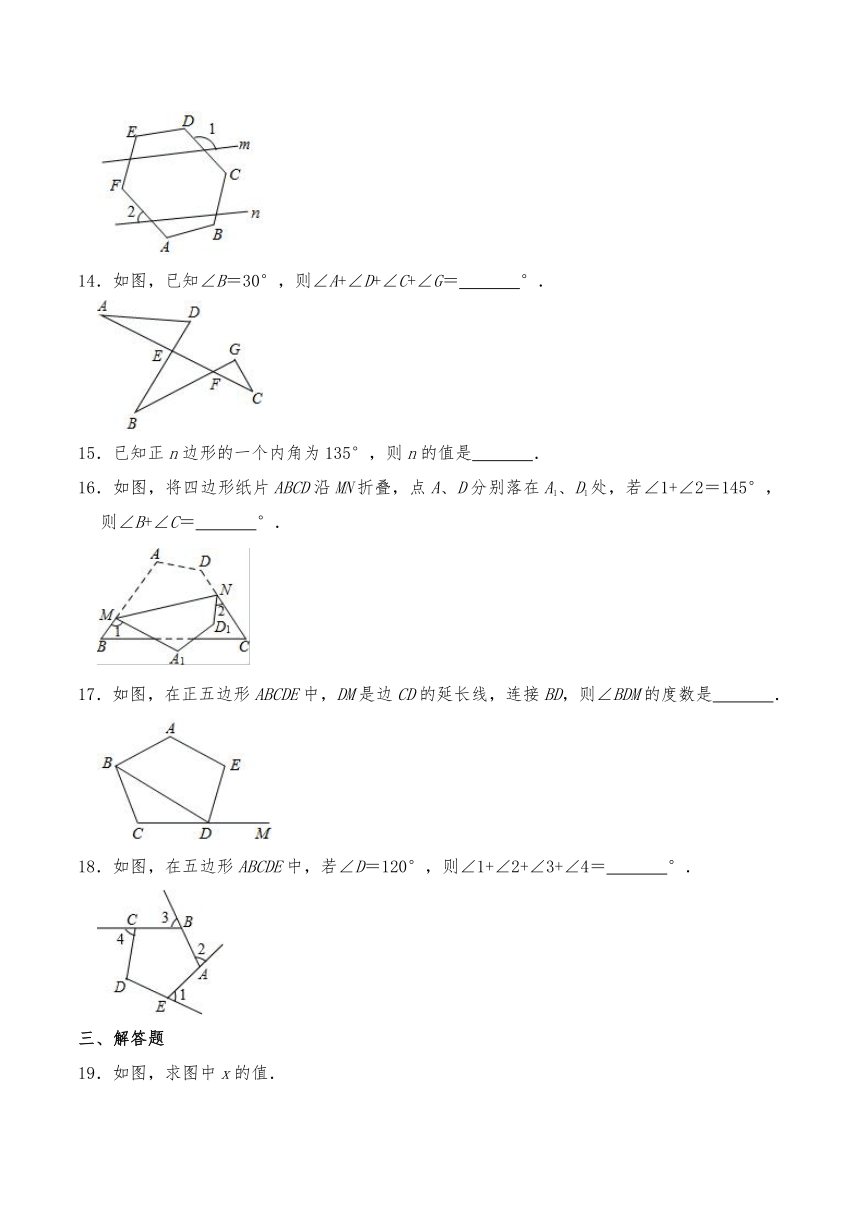
17.如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是
.
18.如图,在五边形ABCDE中,若∠D=120°,则∠1+∠2+∠3+∠4=
°.
三、解答题
19.如图,求图中x的值.
20.在各个内角都相等的多边形中,一个外角等于一个内角的,求这个多边形每一个内角的度数和它的边数.
21.阅读佳佳与明明的对话,解决下列问题:
(1)“多边形内角和为2020°”,为什么不可能?
(2)佳佳求的是几边形的内角和?
(3)错当成内角和那个外角为多少度?
22.如图,在四边形ABCD中,∠C+∠D=210°
(1)∠DAB+∠CBA=
度;
(2)若∠DAB的角平分线与∠CBA的角平分线相交于点E,求∠E的度数.
23.已知:在四边形ABCD中,∠A=∠C=90°.
(1)如图1,求∠B与∠D的和为多少度?
(2)如图2,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F,求证:BE∥DF.
24.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
答案
一、选择题
1.D.2.D.3.D.4.B.5.D.6.D.7.C.8.C.9.C.10.C.
二、填空题
11.十二.
12.45°.
13.180.
14.210.
15.8.
16.107.5°.
17.144°.
18.300.
三、解答题
19.由题意可得,5x=360,
解得x=72.
20.设这个多边形的每一个内角为x°,那么180﹣xx,
解得x=150,
那么边数为360÷(180﹣150)=12.
答:这个多边形的每一个内角的度数为150,它的边数为12.
21.(1)设多边形的边数为n,
180°(n﹣2)=2020°,
解得,
∵n为正整数,
∴“多边形的内角和为2020°”不可能.
(2)设应加的内角为x,多加的外角为y,
依题意可列方程:(n﹣2)180°=2020°﹣y+x,
∵﹣180°<x﹣y<180,
∴2020°﹣180°<180°(n﹣2)<2020°+180°,
解得,
又∵n为正整数,
∴n=13,n=14.
故佳佳求的是十三边形或十四边形的内角和.
(3)十三边的内角和:180°×(13﹣2)=1980°,
∴y﹣x=2020°﹣1980°=40°,
又x+y=180°,
解得:x=70°,y=110°;
十四边的内角和:180°×(13﹣2)=2160°,
∴y﹣x=2160°﹣2020°=140°,
又x+y=180°,
解得:x=160°,y=20°;
所以那个外角为110°或20°.
22.(1)∵∠DAB+∠CBA+∠C+∠D=360°,
∴∠DAB+∠CBA=360°﹣(∠C+∠D)=360°﹣210°=150°.
故答案为:150;
(2)∵∠DAB与∠ABC的平分线交于四边形内一点E,
∴∠EAB∠DAB,∠EBA∠ABC,
∴∠E=180°﹣(∠EAB+∠EBA)
=180°(∠DAB+∠CBA)
=180°(360°﹣∠C﹣∠D)
(∠C+∠D),
∵∠C+∠D=210°,
∴∠E(∠C+∠D)=105°.
23.(1)解:∵∠A=∠C=90°,
∴∠B+∠D+∠A+∠C=(4﹣2)×180°=360°,
∴∠B+∠D=360°﹣∠A﹣∠C=180°;
即∠B与∠D的和为180度;
(2)证明:∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°﹣∠A﹣∠C=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE+∠EDF=90°,
∵∠ABE+∠AEB=90°,
∴∠AEB=∠ADF,
∴BE∥DF.
24.(1)∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°;
(3)根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,
所以当截去5个角时增加了180×5度,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
一、选择题
1.内角和为720°的多边形是( )
A.
B.
C.
D.
2.如果一个正多边形的内角和是外角和的3倍,那么这个正多边形的边数为( )
A.5
B.6
C.7
D.8
3.设四边形的内角和等于a,五边形的内角和等于b,则a与b的关系是( )
A.a>b
B.a=b
C.a=b+180°
D.b=a+180°
4.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为( )
A.100米
B.80米
C.60米
D.40米
5.若某多边形的边数增加1,则这个多边形的外角和( )
A.增加180°
B.增加360°
C.减少180°
D.不变
6.若正多边形的一个外角是36°,则该正多边形的内角和为( )
A.360°
B.720°
C.900°
D.1440°
7.如图,过正六边形ABCDEF的顶点B作一条射线与其内角∠BAF的角平分线相交于点P,且∠APB=40°,则∠CBP的度数为( )
A.80°
B.60°
C.40°
D.30°
8.如图,AP,CP分别是四边形ABCD的外角∠DAM,∠DCN的平分线,设∠ABC=α,∠APC=β,则∠ADC的度数为( )
A.180°﹣α﹣β
B.α+β
C.α+2β
D.2α+β
9.如图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360°
B.540°
C.630°
D.720°
10.如图,以正五边形ABCDE的对角线BE为边,作正方形BEFG,使点A落在正方形BEFG内,则∠ABG的度数为( )
A.18°
B.36°
C.54°
D.72°
二、填空题
11.一个多边形的每一个内角都等于150°,这个多边形共有
条边.
12.若正多边形的内角和是外角和的3倍,则这个正多边形的每个外角等于
.
13.如图,六边形ABCDEF的各角都相等,若m∥n,则∠1+∠2=
°.
14.如图,已知∠B=30°,则∠A+∠D+∠C+∠G=
°.
15.已知正n边形的一个内角为135°,则n的值是
.
16.如图,将四边形纸片ABCD沿MN折叠,点A、D分别落在A1、D1处,若∠1+∠2=145°,则∠B+∠C=
°.
17.如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是
.
18.如图,在五边形ABCDE中,若∠D=120°,则∠1+∠2+∠3+∠4=
°.
三、解答题
19.如图,求图中x的值.
20.在各个内角都相等的多边形中,一个外角等于一个内角的,求这个多边形每一个内角的度数和它的边数.
21.阅读佳佳与明明的对话,解决下列问题:
(1)“多边形内角和为2020°”,为什么不可能?
(2)佳佳求的是几边形的内角和?
(3)错当成内角和那个外角为多少度?
22.如图,在四边形ABCD中,∠C+∠D=210°
(1)∠DAB+∠CBA=
度;
(2)若∠DAB的角平分线与∠CBA的角平分线相交于点E,求∠E的度数.
23.已知:在四边形ABCD中,∠A=∠C=90°.
(1)如图1,求∠B与∠D的和为多少度?
(2)如图2,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F,求证:BE∥DF.
24.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
答案
一、选择题
1.D.2.D.3.D.4.B.5.D.6.D.7.C.8.C.9.C.10.C.
二、填空题
11.十二.
12.45°.
13.180.
14.210.
15.8.
16.107.5°.
17.144°.
18.300.
三、解答题
19.由题意可得,5x=360,
解得x=72.
20.设这个多边形的每一个内角为x°,那么180﹣xx,
解得x=150,
那么边数为360÷(180﹣150)=12.
答:这个多边形的每一个内角的度数为150,它的边数为12.
21.(1)设多边形的边数为n,
180°(n﹣2)=2020°,
解得,
∵n为正整数,
∴“多边形的内角和为2020°”不可能.
(2)设应加的内角为x,多加的外角为y,
依题意可列方程:(n﹣2)180°=2020°﹣y+x,
∵﹣180°<x﹣y<180,
∴2020°﹣180°<180°(n﹣2)<2020°+180°,
解得,
又∵n为正整数,
∴n=13,n=14.
故佳佳求的是十三边形或十四边形的内角和.
(3)十三边的内角和:180°×(13﹣2)=1980°,
∴y﹣x=2020°﹣1980°=40°,
又x+y=180°,
解得:x=70°,y=110°;
十四边的内角和:180°×(13﹣2)=2160°,
∴y﹣x=2160°﹣2020°=140°,
又x+y=180°,
解得:x=160°,y=20°;
所以那个外角为110°或20°.
22.(1)∵∠DAB+∠CBA+∠C+∠D=360°,
∴∠DAB+∠CBA=360°﹣(∠C+∠D)=360°﹣210°=150°.
故答案为:150;
(2)∵∠DAB与∠ABC的平分线交于四边形内一点E,
∴∠EAB∠DAB,∠EBA∠ABC,
∴∠E=180°﹣(∠EAB+∠EBA)
=180°(∠DAB+∠CBA)
=180°(360°﹣∠C﹣∠D)
(∠C+∠D),
∵∠C+∠D=210°,
∴∠E(∠C+∠D)=105°.
23.(1)解:∵∠A=∠C=90°,
∴∠B+∠D+∠A+∠C=(4﹣2)×180°=360°,
∴∠B+∠D=360°﹣∠A﹣∠C=180°;
即∠B与∠D的和为180度;
(2)证明:∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°﹣∠A﹣∠C=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE+∠EDF=90°,
∵∠ABE+∠AEB=90°,
∴∠AEB=∠ADF,
∴BE∥DF.
24.(1)∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°;
(3)根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,
所以当截去5个角时增加了180×5度,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
