数学人教A版选修1-1 3.2函数单调性与导数(课件)(共25张PPT)
文档属性
| 名称 | 数学人教A版选修1-1 3.2函数单调性与导数(课件)(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
函数的单调性
与导数
知识导学
知识导学
问题探究
探究1:
利用导数判断函数图象
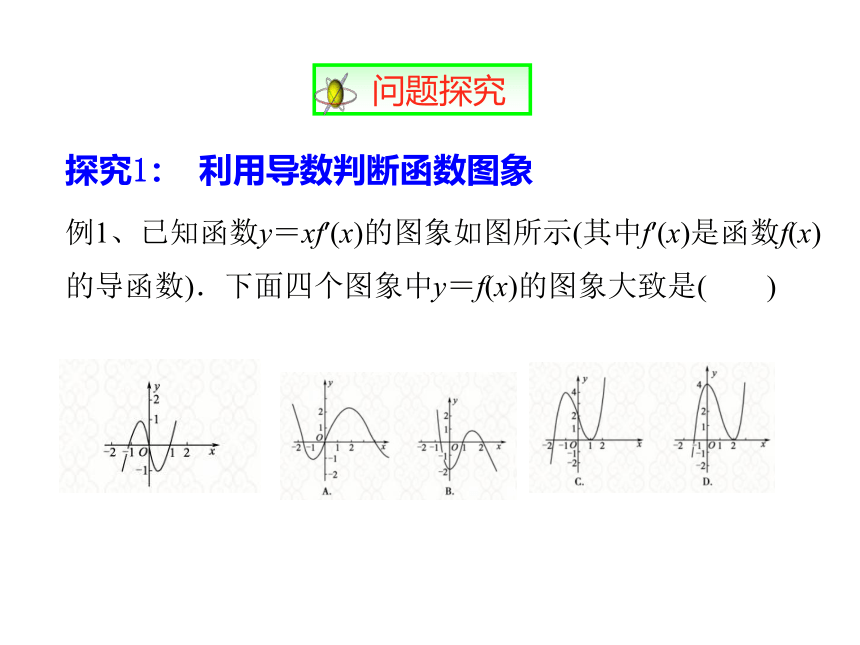
例1、已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数).下面四个图象中y=f(x)的图象大致是( )
解析: 当x<-1时,xf′(x)<0,
∴f′(x)>0,f(x)为增函数,
当-10,
∴f′(x)<0,f(x)为减函数,
当0∴f′(x)<0,f(x)为减函数,
当x>1时,xf′(x)>0,f′(x)>0,f(x)为增函数.
答案:C
归纳总结
根据题目条件和所给图象,判断f′(x)所在区间函数值的符号,确定f(x)所在区间的单调性,大致可以确定曲线的形状.
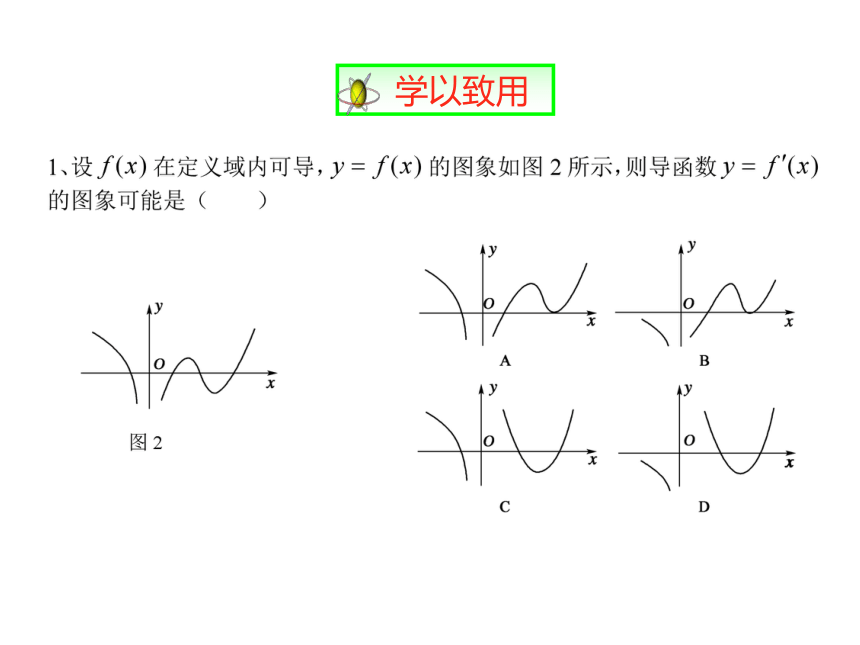
学以致用
问题探究
探究2:
求函数的单调区间
归纳总结
学以致用
2、设函数f(x)=xekx(k≠0)
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)的单调区间.
(1)f′(x)=(1+kx)ekx,f′(0)=1,f(0)=0,
曲线y=f(x)在点(0,f(0))处的切线方程为y=x.
问题探究
探究3:
由函数的单调性求参数的范围
归纳总结
学以致用
C
当堂检测
课堂小结
2
求含参函数的单调区间
3
利用函数单调性求参数范围
1
函数与导函数图像关系
作
业
生活中没有什么可怕的东西,只有需要理解的东西.
——居里夫人
1完成创新设计251页第3-5题
2有能力的同学完成252页第7题
函数的单调性
与导数
知识导学
知识导学
问题探究
探究1:
利用导数判断函数图象
例1、已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数).下面四个图象中y=f(x)的图象大致是( )
解析: 当x<-1时,xf′(x)<0,
∴f′(x)>0,f(x)为增函数,
当-1
∴f′(x)<0,f(x)为减函数,
当0
当x>1时,xf′(x)>0,f′(x)>0,f(x)为增函数.
答案:C
归纳总结
根据题目条件和所给图象,判断f′(x)所在区间函数值的符号,确定f(x)所在区间的单调性,大致可以确定曲线的形状.
学以致用
问题探究
探究2:
求函数的单调区间
归纳总结
学以致用
2、设函数f(x)=xekx(k≠0)
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)的单调区间.
(1)f′(x)=(1+kx)ekx,f′(0)=1,f(0)=0,
曲线y=f(x)在点(0,f(0))处的切线方程为y=x.
问题探究
探究3:
由函数的单调性求参数的范围
归纳总结
学以致用
C
当堂检测
课堂小结
2
求含参函数的单调区间
3
利用函数单调性求参数范围
1
函数与导函数图像关系
作
业
生活中没有什么可怕的东西,只有需要理解的东西.
——居里夫人
1完成创新设计251页第3-5题
2有能力的同学完成252页第7题
