数学人教A版(2019)必修第一册4.2指数函数(课件)(共16张PPT)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.2指数函数(课件)(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 601.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 10:57:00 | ||
图片预览




文档简介
(共16张PPT)
指数函数
创设情景
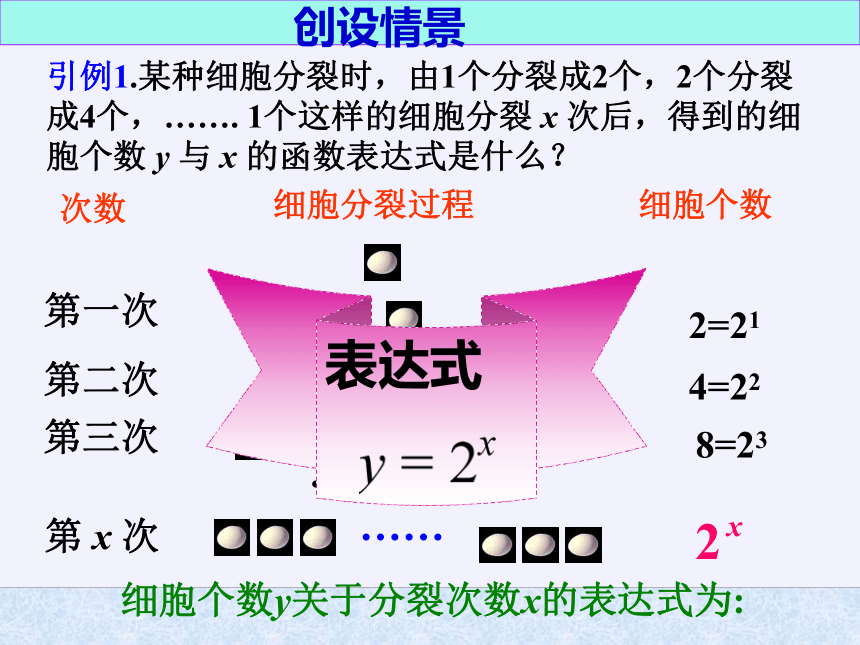
引例1.某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…….
1个这样的细胞分裂
x
次后,得到的细胞个数
y
与
x
的函数表达式是什么?
次数
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第
x
次
……
细胞个数y关于分裂次数x的表达式为:
表达式
创设情景
引例2
、
(2).一根1米长的绳子从中间剪一次剩下
米,再从中
间剪一次剩下
米,若这条绳子剪x次剩下y米,
则y与x的函数表达式是:
引入概念与剖析
1.指数函数的定义:
形如y
=
ax(a?0,且a
?1)的函数叫做指数函数,其中x是自变量
.
函数的定义域是R
.
概念剖析
指数函数解析式有什么特点?
下列哪些是指数函数?
思考2:
(1)
y=x2
y=2x
(3)
y=2-x
(4)
y=2
·
3x
(5)
y=23x
(6)
y=3x+1
⒉
的系数是1
;
指数函数的解析式
,
⒈底数a?0,且a?1.
指数必须是单个x
;
⒊
动手操作,
画出图像
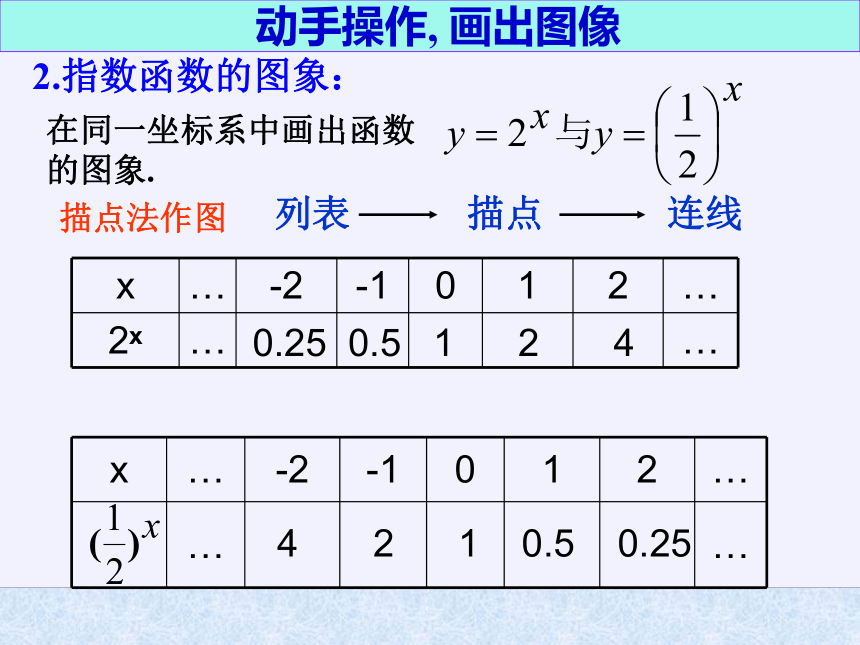
2.指数函数的图象:
在同一坐标系中画出函数
的图象.
x
…
-2
-1
0
1
2
…
2x
…
…
描点法作图
列表
描点
连线
x
…
-2
-1
0
1
2
…
…
…
0.25
0.5
1
2
4
4
2
1
0.5
0.25
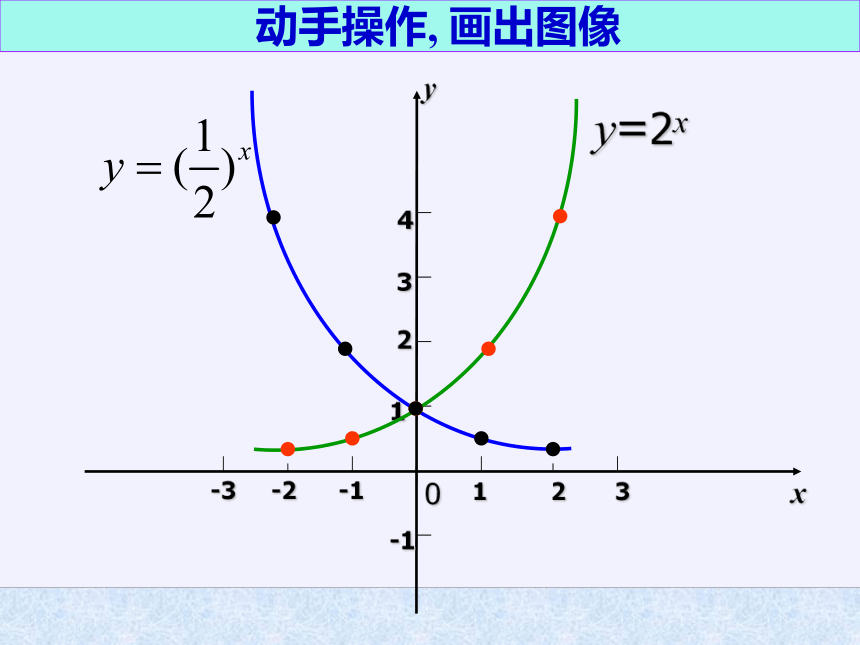
动手操作,
画出图像
-1
1
2
3
-3
-2
-1
4
3
2
1
0
y
x
y=2x
动手操作,
画出图像
观察以上四个函数的图象,你发现了什么特征?有何异同?
图
象
性
质
a>1
0y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定
义
域
:
值
域
:
必过
点:
在
R
上是
在
R
上是
R
(
0
,
+
∞
)
(
0
,
1
)
,即
x
=
0
时,
y
=
1
.
增函数
减函数
x>0,y>1;
x<0,y>1;
x<0,
0x>0,0观察图像,
得出性质
解:
例1
例2.
比较下列各题中两个值的大小:
(1)1.72.5
,
1.73
;
(2)0.8-0.1
,0.8
-0.2
(3)1.70.3
,
0.93.1.
应用新知
小结
比较指数幂大小的方法:
①、单调性法:利用函数的单调性,数的特征
是底同指不同(包括可以化为同底的)。
②、中间值法:找一个
“中间值”如“1”来过渡,
数的特征是底不同指不同。
<
<
>
练习1.
比较大小:
(1)3.10.5
,
3.12.3
(2)
(3)
2.3-2.5
,
0.2
-0.1
应用新知
<
<
>
1.函数是
指数函数,则
=________
3
(0,4)
3.函数
是减函数,求
的取值范围.
4.已知0.3x≥0.37,求实数x的取值范围.
5.已知
5x<
,
求实数x的取值范围.
x<-2
(1).指数函数
中的
(2).函数
的图象恒过点
(3).若指数函数
是减函数,求实数
的取值范围.
(4).函数
在
上的最大值比最小值大
则
(5).
函数
为奇函数则
(6).设
它的最小值是
(7).求
在定义域上的单调性
感悟收获,巩固拓展
1、总结反思
这节课我学到了哪些数学知识和数学思想方法?
2、课后作业
谢
谢
指数函数
创设情景
引例1.某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…….
1个这样的细胞分裂
x
次后,得到的细胞个数
y
与
x
的函数表达式是什么?
次数
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第
x
次
……
细胞个数y关于分裂次数x的表达式为:
表达式
创设情景
引例2
、
(2).一根1米长的绳子从中间剪一次剩下
米,再从中
间剪一次剩下
米,若这条绳子剪x次剩下y米,
则y与x的函数表达式是:
引入概念与剖析
1.指数函数的定义:
形如y
=
ax(a?0,且a
?1)的函数叫做指数函数,其中x是自变量
.
函数的定义域是R
.
概念剖析
指数函数解析式有什么特点?
下列哪些是指数函数?
思考2:
(1)
y=x2
y=2x
(3)
y=2-x
(4)
y=2
·
3x
(5)
y=23x
(6)
y=3x+1
⒉
的系数是1
;
指数函数的解析式
,
⒈底数a?0,且a?1.
指数必须是单个x
;
⒊
动手操作,
画出图像
2.指数函数的图象:
在同一坐标系中画出函数
的图象.
x
…
-2
-1
0
1
2
…
2x
…
…
描点法作图
列表
描点
连线
x
…
-2
-1
0
1
2
…
…
…
0.25
0.5
1
2
4
4
2
1
0.5
0.25
动手操作,
画出图像
-1
1
2
3
-3
-2
-1
4
3
2
1
0
y
x
y=2x
动手操作,
画出图像
观察以上四个函数的图象,你发现了什么特征?有何异同?
图
象
性
质
a>1
0
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
义
域
:
值
域
:
必过
点:
在
R
上是
在
R
上是
R
(
0
,
+
∞
)
(
0
,
1
)
,即
x
=
0
时,
y
=
1
.
增函数
减函数
x>0,y>1;
x<0,y>1;
x<0,
0
得出性质
解:
例1
例2.
比较下列各题中两个值的大小:
(1)1.72.5
,
1.73
;
(2)0.8-0.1
,0.8
-0.2
(3)1.70.3
,
0.93.1.
应用新知
小结
比较指数幂大小的方法:
①、单调性法:利用函数的单调性,数的特征
是底同指不同(包括可以化为同底的)。
②、中间值法:找一个
“中间值”如“1”来过渡,
数的特征是底不同指不同。
<
<
>
练习1.
比较大小:
(1)3.10.5
,
3.12.3
(2)
(3)
2.3-2.5
,
0.2
-0.1
应用新知
<
<
>
1.函数是
指数函数,则
=________
3
(0,4)
3.函数
是减函数,求
的取值范围.
4.已知0.3x≥0.37,求实数x的取值范围.
5.已知
5x<
,
求实数x的取值范围.
x<-2
(1).指数函数
中的
(2).函数
的图象恒过点
(3).若指数函数
是减函数,求实数
的取值范围.
(4).函数
在
上的最大值比最小值大
则
(5).
函数
为奇函数则
(6).设
它的最小值是
(7).求
在定义域上的单调性
感悟收获,巩固拓展
1、总结反思
这节课我学到了哪些数学知识和数学思想方法?
2、课后作业
谢
谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
