八年级数学一次函数的应用

(共28张PPT)
25.5
河北省深州市于科中学 于藏娟
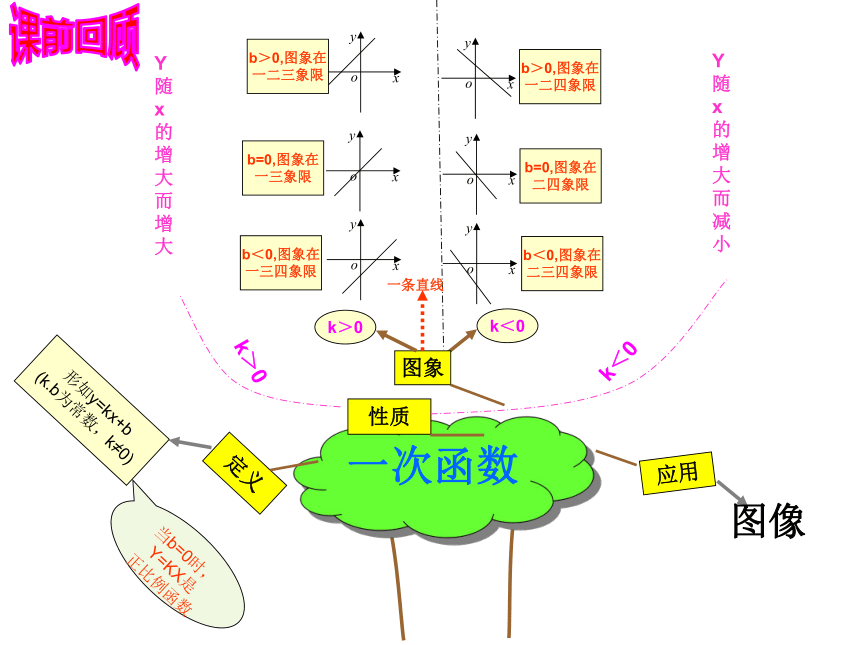
一次函数
k＜0
b＜0,图象在
二三四象限
b=0,图象在
二四象限
b＞0,图象在
一二四象限
定义
形如y=kx+b
(k.b为常数，k≠0)
当b=0时，Y=KX是
正比例函数
图象
k＞0
b＜0,图象在
一三四象限
b=0,图象在
一三象限
b＞0,图象在
一二三象限
一条直线
性质
k＞0
k＜0
Y随x的增大而增大
Y随x的增大而减小
应用
图像
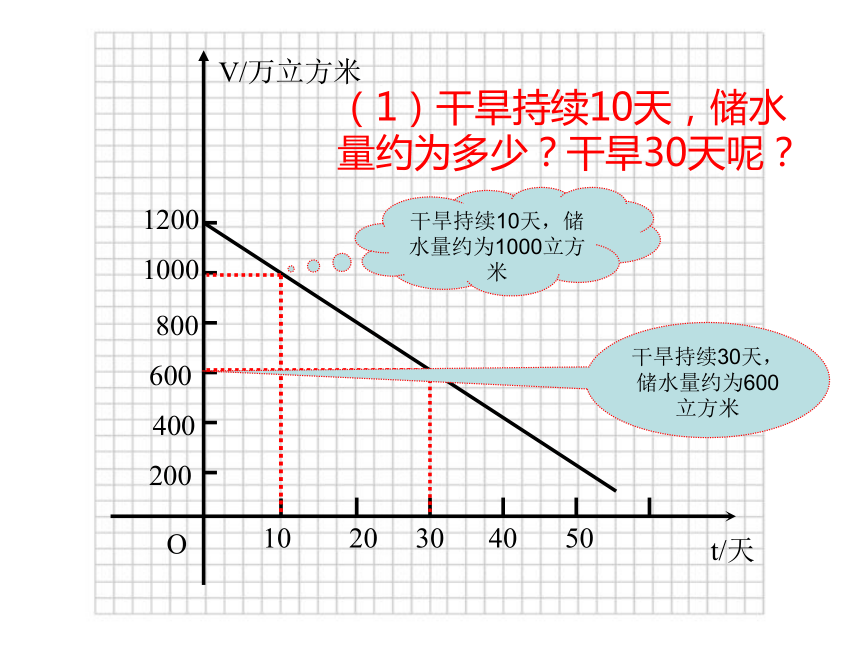
引例：1、由于持续的高温和连日无雨某水 库的储水量随着时间的增加而减少，干 旱持续了t（天）与储水量V（万立方 米 ）的关系如下图所示：
40
400
800
O
10
20
30
50
t/天
200
600
1000
1200
V/万立方米
10
20
30
40
50
t/天
200
400
600
800
1000
1200
O
V/万立方米
（1）干旱持续10天，储水量约为多少？干旱30天呢？
干旱持续10天，储水量约为1000立方米
干旱持续30天，储水量约为600立方米
10
20
30
40
50
t/天
200
400
600
800
1000
1200
O
V/万立方米
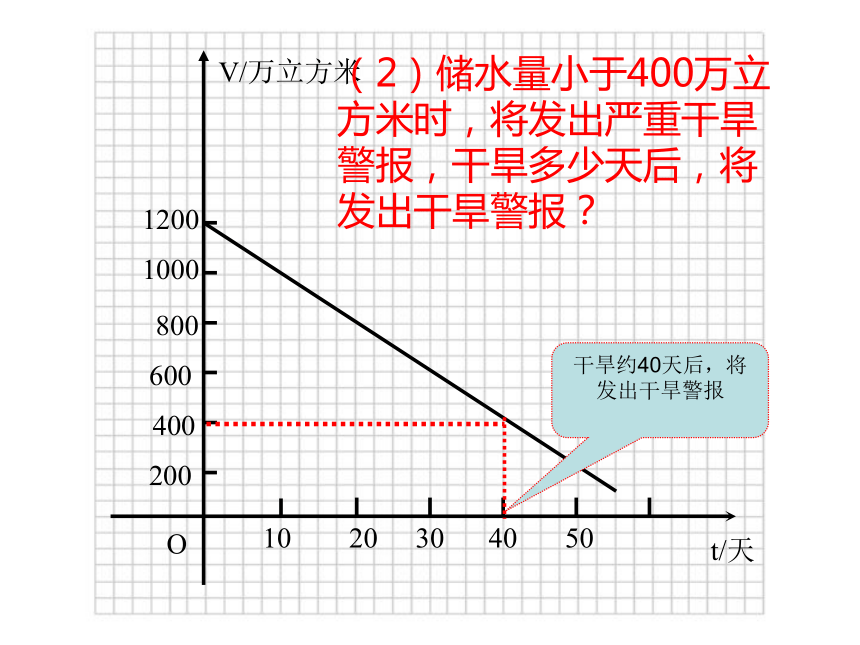
（2）储水量小于400万立方米时，将发出严重干旱警报，干旱多少天后，将发出干旱警报？
干旱约40天后，将发出干旱警报










1
2
3
4
5
6
7
8
10
1
2
3
4
5
6
9
10


7
8









9
t /天


y /厘米
l
O
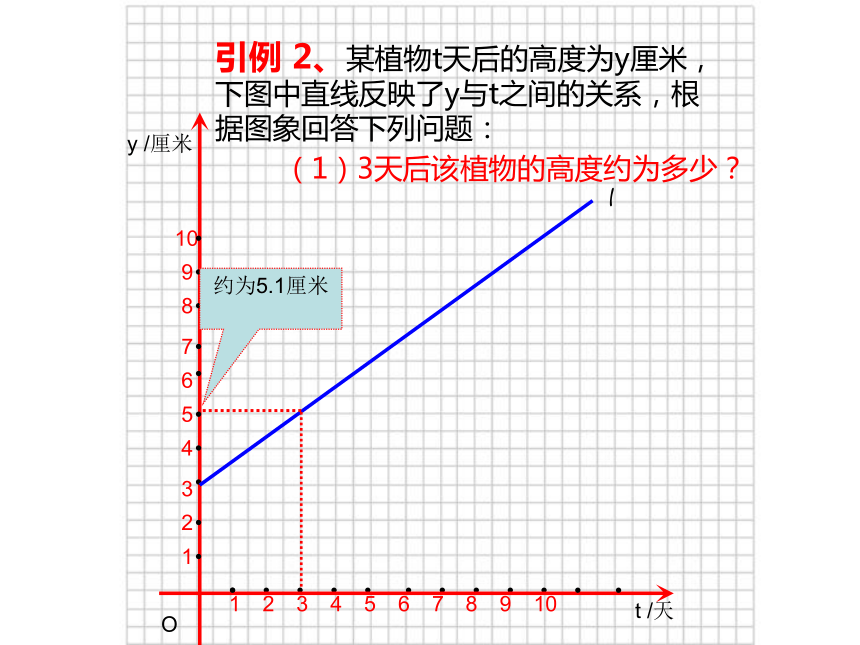
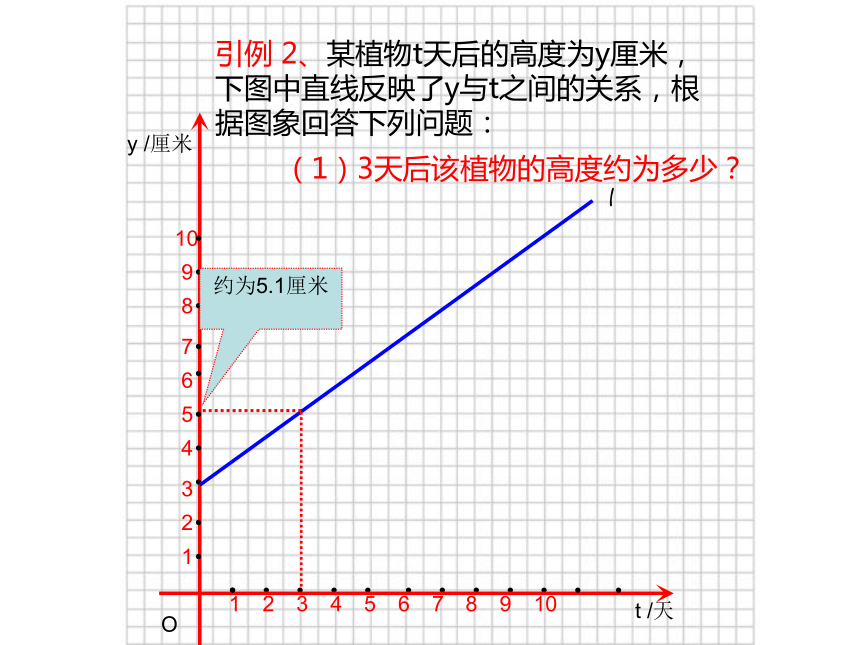
引例 2、某植物t天后的高度为y厘米，下图中直线反映了y与t之间的关系，根据图象回答下列问题：
（1）3天后该植物的高度约为多少？
约为5.1厘米










1
2
3
4
5
6
7
8
10
1
2
3
4
5
6
9
10


7
8









9
t /天


y /厘米
l
O
引例 2、某植物t天后的高度为y厘米，下图中直线反映了y与t之间的关系，根据图象回答下列问题：
（1）3天后该植物的高度约为多少？
约为5.1厘米










1
2
3
4
5
6
7
8
10
1
2
3
4
5
6
9
10


7
8









9
t /天


Y /厘米
l
O
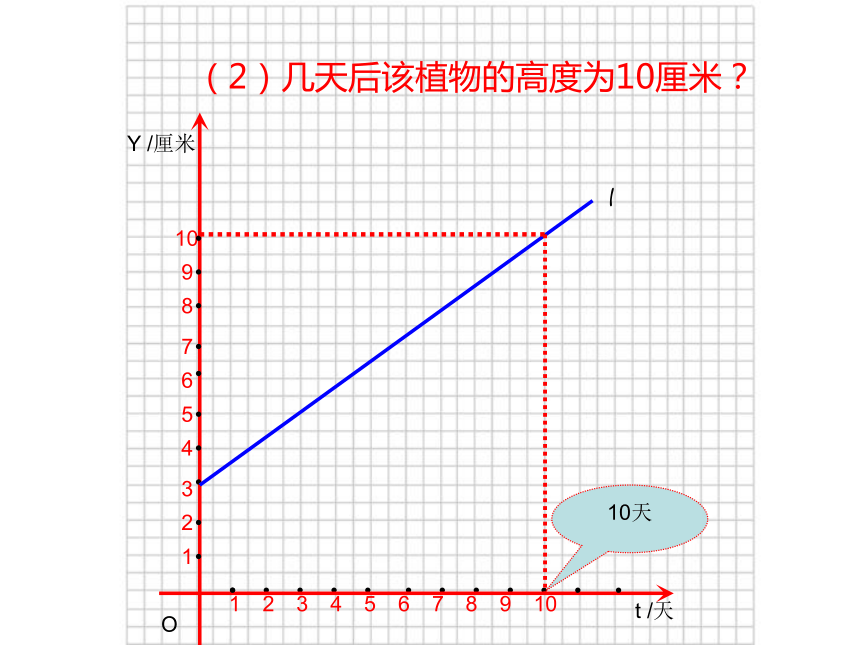
（2）几天后该植物的高度为10厘米？
10天










1
2
3
4
5
6
7
8
10
1
2
3
4
5
6
9
10


7
8









9
t /天


l
y /厘米

O
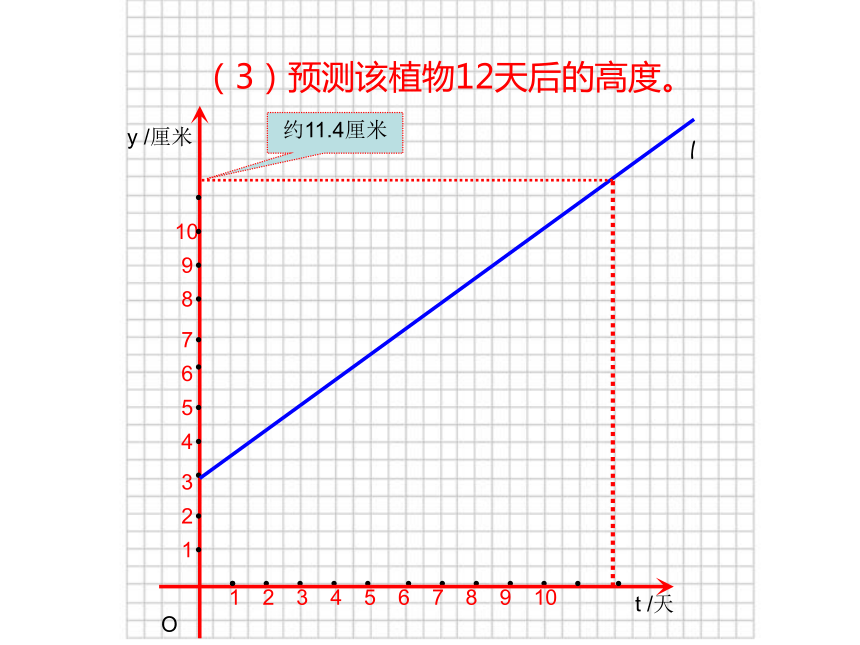
（3）预测该植物12天后的高度。
约11.4厘米
张大伯出去散步，从家走了20分钟，到了一个离家900米的阅报亭，看了10分钟报纸后，用了15分钟返回到家。下面哪个图象表示张大伯离家时间与距离之间的关系？ （ ）
时间（分）
距离（米）
时间（分）
10 20 30 40 50
900
0
A
0
时间（分）
距离（米）
10 20 30 40 50
900
B
距离（米）
900
C
10 20 30 40 50
0
900
10 20 3 0 40 50
0
时间（分）
距离（米）
D
D
请你判断
x(吨)
y(元)
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1 反映了某公司产品的销售收入与销售量的关系，根据图象回答：
l1
(1)当销售量为2吨时，销售收入＝　　　　元，
销售收入
2000
(2)l1对应的函数表达式是　　　　　　　　，
y=1000x
共同探究
x(吨)
y(元)
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2
(1)当销售成本＝4500元时，销售量＝　　吨；
5
l2 反映了该公司产品的销售成本与销售量的
关系， 根据图象回答：
销售成本
　　(2)l2对应的函数表达式是　　　　　　　　。
y=500x+2000
x(吨)
y(元)
O
1
2
3
4
5
6
L1
销售收入
1000
4000
5000
2000
3000
6000
l1 反映了公司产品的销售收入与销售量的关系。
l2 反映了公司产品的销售成本与销售量的关系。
L2销售成本
x(吨)
y(元)
O
1
2
3
4
5
6
l2
销售成本
1000
4000
5000
2000
3000
6000
x(吨)
y(元)
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
（1）当销售量为6吨时，销售收入＝　　　　元，
　　 销售成本＝　　　元， 利润＝　　　　元。
6000
5000
销售收入
销售成本
1000
（2）你还能得到什么信息？
x(吨)
y(元)
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
销售收入
销售成本
5
6
1
2
3
P
7
8
（2）你还能得到什么信息？
1.小明与小李一天去游泳馆进行1000米
游泳训练,他们在长为50米的泳道上分别在泳道
的两端出发,若都以2米/秒的速度向对面游去,游
到对岸之后马上返回,并且在游泳过程中保持匀
速,当两人同时游完后,他们在游泳过程中,总共
相遇了______次.
试着做做（1）
1.小明与小李一天去游泳馆进行1000米
游泳训练,他们在长为50米的泳道上分别在泳道
的两端出发,若都以2米/秒的速度向对面游去,游
到对岸之后马上返回,并且在游泳过程中保持匀
速,当两人同时游完后,他们在游泳过程中,总共
相遇了______次.
填一填
t(秒)
s(米)
O
50
25
25
50
75
100
125
150
175
200
225
250
20
2.下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象.根据图象回答问题:
s (米)
1
2
3
4
5
O
100
20
120
40
60
80
t(分)
6
8
7
-1
12
9
10
11
-3
-2
l1
l2
-4
试着做做（2）
（1）乌龟与兔子___时,___地出发,____时到达终点.
（填“同”或“不同”）
同
同
不同
2.下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象.根据图象回答问题:
（2）这一次是 　米赛跑。
（3）表示兔子赛跑的图象是 。
100
l2
s (米)
1
2
3
4
5
O
100
20
120
40
60
80
t(分)
6
8
7
-1
12
9
10
11
-3
-2
l1
l2
-4
填一填
A
s (米)
（3）当兔子到达终点时，乌龟距终点还有 　米。
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
t (分)
6
8
7
（4）乌龟要与兔子同时到达终点乌龟要先跑 米。
-1
12
9
10
11
-3
-2
40
-4
40
想一想:你觉得如果让兔子后退40米,两者再同时
起跑,它们能同时到达终点吗
A
s (米)
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
t (分)
6
8
7
-1
12
9
10
11
-3
-2
-4
想一想:你觉得如果让兔子后退40米,两者再同时
起跑,它们能同时到达终点吗
-20
-40
下表是某水果市场香蕉的价格情况:
购买香蕉的数量
(千克) 不超过20
千克 20千克以上,不
超过40千克
每千克价格 6元 5元
（1）试写出所付金额y（元）随购买香蕉数量x（千克）
变化的函数关系式；
（2）画出函数图象；
（3）现有60元全部用于购买香蕉,你能买多少千克香蕉
思考:购买香蕉的金额在怎样的范围内,可以用同样的钱
买更多的香蕉
（4）若现有108元全部用于购买香蕉,你会怎样购买
y(元)
O
1
2
3
50
150
100
200
5
10
15
20
25
30
35
40
x(千克)
120
画函数图象
y=6x (0≤x≤20)
y=5x (201、如图表示一艘轮船和一艘快艇
沿相同路线从甲港出发到乙港行
驶过程中,路程随时间变化的图象
（分别是正比例函数图象和一次
函数图象）．根据图象解答下列
问题：
(1)请分别求出表示轮船和快艇行
驶过程的函数解析式（不要求写
出自变量的取值范围）；
(2)轮船和快艇在途中行驶的速度分别是多少？
(3)问快艇出发多长时间赶上轮船？
o
2
5
3
6
x/小时
y/ 微克
2. 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)变化情况如图所示,当成人按规定剂量服药后.
(1)服药后 时,血液中含药量最高,达每毫升 微克,接着逐步衰减.
(2)服药后5时,血液中含药量为每毫升 微克
(3)当x≤2时,y与x之间的函数关系式是
(4)当x≥2时,y与x之间的函数关系式是
(5)如果每毫克血液中含药量度3微克或3微克以上时,治疗疾病最有效,
那么这个有效时间范围是 时
一次函数的概念
一次函数的内容
一次函数的图像和性质
一般一次函数
一次函数的应用
待定系数法
特殊的一次函数
一条直线
图像经过象限的情况
画一次函数图像的妙法
增减性
图像的应用
生活中的问题
代数式
方程
不等式
坐标系
一次函数表达式的确定
根据题意直接写
知识小结
达标测评：我边防局接到情报，近海处有一可疑船只A正向公海方向行驶，边防局迅速派出快艇B追赶（如图所示）。图中 L1 ，L2 分别表示两船相对于海岸的距离s（海里）与追赶时间t（分）之间的关系
根据图象回答下列问题
1 ） 哪条线表示B到海岸的距离与追赶时间之间的关系？
2） A，B哪个速度快
3） 15分内B能否追上A？
4）如果一直追下去，那么B能否追上A？
5）当A逃到离海岸12海里时，B将无法对其进行检查。照此速度，B能否在A逃入公海前将其拦截？
s/海里
1 2 3 4 5 6 7 8 9
1
2
3
4
5
6
7
8
0
L1
L2
t/分
敬请指教
谢谢