3.1 对函数的再认识课件(共40张PPT)
文档属性
| 名称 | 3.1 对函数的再认识课件(共40张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 00:00:00 | ||
图片预览








文档简介
(共40张PPT)
第三章
二次函数
1
对函数的再认识
知识点一
函数的定义
一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x在某一范围内的每一个确定值,变量y都有唯一确定的值与它对应,那么我们就称y是x的函数,其中x是自变量,y是因变量.
知识解读
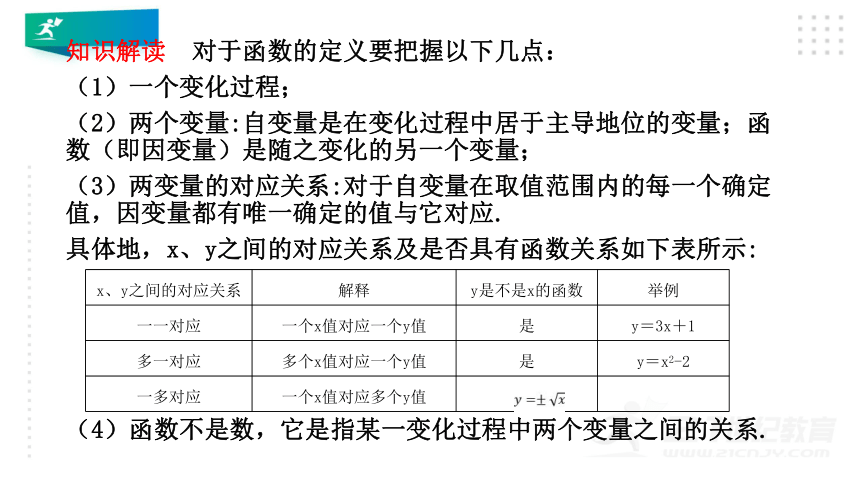
对于函数的定义要把握以下几点:
(1)一个变化过程;
(2)两个变量:自变量是在变化过程中居于主导地位的变量;函数(即因变量)是随之变化的另一个变量;
(3)两变量的对应关系:对于自变量在取值范围内的每一个确定值,因变量都有唯一确定的值与它对应.
具体地,x、y之间的对应关系及是否具有函数关系如下表所示:
(4)函数不是数,它是指某一变化过程中两个变量之间的关系.
x、y之间的对应关系
解释
y是不是x的函数
举例
一一对应
一个x值对应一个y值
是
y=3x+1
多一对应
多个x值对应一个y值
是
y=x2-2
一多对应
一个x值对应多个y值
否
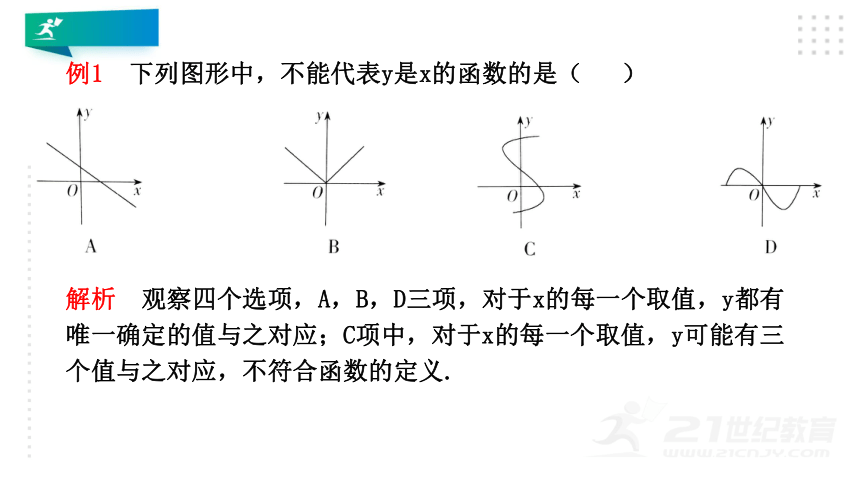
例1
下列图形中,不能代表y是x的函数的是(
)
例1
下列图形中,不能代表y是x的函数的是(
)
解析
观察四个选项,A,B,D三项,对于x的每一个取值,y都有唯一确定的值与之对应;C项中,对于x的每一个取值,y可能有三个值与之对应,不符合函数的定义.
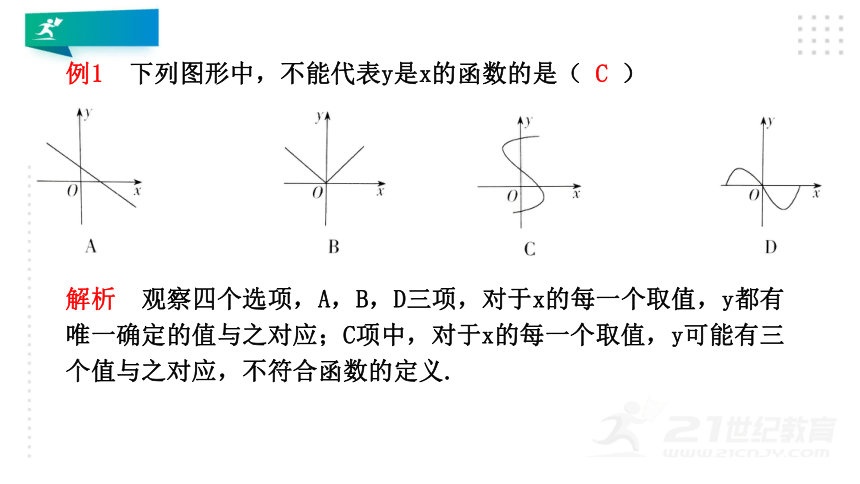
例1
下列图形中,不能代表y是x的函数的是(
C
)
解析
观察四个选项,A,B,D三项,对于x的每一个取值,y都有唯一确定的值与之对应;C项中,对于x的每一个取值,y可能有三个值与之对应,不符合函数的定义.
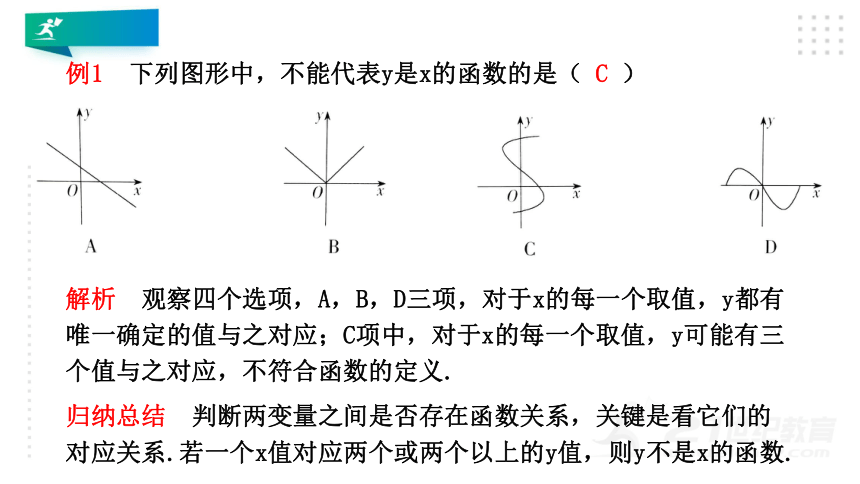
例1
下列图形中,不能代表y是x的函数的是(
C
)
解析
观察四个选项,A,B,D三项,对于x的每一个取值,y都有唯一确定的值与之对应;C项中,对于x的每一个取值,y可能有三个值与之对应,不符合函数的定义.
归纳总结
判断两变量之间是否存在函数关系,关键是看它们的对应关系.若一个x值对应两个或两个以上的y值,则y不是x的函数.
知识点二
函数值
对于自变量x在某一范围内的一个确定的值a,函数y有唯一确定的对应值,这个对应值叫做当x=a时函数的值简称函数值.
知识点二
函数值
对于自变量x在某一范围内的一个确定的值a,函数y有唯一确定的对应值,这个对应值叫做当x=a时函数的值简称函数值.
温馨提示
(1)当已知函数解析式及自变量的值,欲求函数值时,实质就是求代数式的值.
(2)当已知函数解析式,又给出函数值,欲求相应的自变量的值时,实质就是解方程.
(3)当给定函数值的一个取值范围,欲求相应的自变量的取值范围时,实质就是解不等式.
(4)当自变量确定时,函数值是唯一确定的.但当函数值唯一确定时,对应的自变量可以是多个,如y=x2-1,当y=3时,x=±2.
知识点三
函数的表示方法
用来表示函数关系的数学式子叫做函数的表达式(或解析式),用数学式子表示函数的方法称为解析法.函数还可以用表格和图象表示,分别称为列表法和图象法.
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
列表法
图象法
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
列表法
图象法
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
不直观,有些实际问题不能用解析式表示出来
列表法
图象法
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
不直观,有些实际问题不能用解析式表示出来
列表法
可以清楚、直接地表示出变量之间的数值对应关系
图象法
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
不直观,有些实际问题不能用解析式表示出来
列表法
可以清楚、直接地表示出变量之间的数值对应关系
有局限性,列出的对应值是有限的
图象法
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
不直观,有些实际问题不能用解析式表示出来
列表法
可以清楚、直接地表示出变量之间的数值对应关系
有局限性,列出的对应值是有限的
图象法
可以直观地表示出函数的变化过程和变化趋势
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
不直观,有些实际问题不能用解析式表示出来
列表法
可以清楚、直接地表示出变量之间的数值对应关系
有局限性,列出的对应值是有限的
图象法
可以直观地表示出函数的变化过程和变化趋势
观察得到的自变量或函数的值是近似的
知识拓展
分段函数
定义
在自变量的取值范围内,对于自变量x的不同取值范围、函数与自变量间有不同的对应关系,这样的函数叫做分段函数
定义解读
确定解析式的方法
求值方法
知识拓展
分段函数
定义
在自变量的取值范围内,对于自变量x的不同取值范围、函数与自变量间有不同的对应关系,这样的函数叫做分段函数
定义解读
(1)对分段函数来说,在不同自变量的取值范围内其对应关系不同,但分段函数是一个函数;
(2)分段函数中自变量的取值范围为各段取值范围的并集,分段函数中函数的取值范围为各段函数的取值范围的并集
确定解析式的方法
求值方法
知识拓展
分段函数
定义
在自变量的取值范围内,对于自变量x的不同取值范围、函数与自变量间有不同的对应关系,这样的函数叫做分段函数
定义解读
(1)对分段函数来说,在不同自变量的取值范围内其对应关系不同,但分段函数是一个函数;
(2)分段函数中自变量的取值范围为各段取值范围的并集,分段函数中函数的取值范围为各段函数的取值范围的并集
确定解析式的方法
(1)分别求出自变量在不同范围内的函数解析式;
(2)用“|”表示出各段解析式,注意写明自变量的取值范围
求值方法
知识拓展
分段函数
定义
在自变量的取值范围内,对于自变量x的不同取值范围、函数与自变量间有不同的对应关系,这样的函数叫做分段函数
定义解读
(1)对分段函数来说,在不同自变量的取值范围内其对应关系不同,但分段函数是一个函数;
(2)分段函数中自变量的取值范围为各段取值范围的并集,分段函数中函数的取值范围为各段函数的取值范围的并集
确定解析式的方法
(1)分别求出自变量在不同范围内的函数解析式;
(2)用“|”表示出各段解析式,注意写明自变量的取值范围
求值方法
(1)先确定要求值的自变量属于哪一段;
(2)代入该段的解析式求值
例3
数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度-20℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到-4℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至-20℃时,制冷再次停止,……按照以上方式循环进行.
同学们记录了“44min内15个时间点冷柜中的温度y(℃)随时间x(min)的变化情况”,制成下表:
时间x/min
…
4
8
10
16
20
21
22
23
24
28
30
36
40
42
44
…
温度y/℃
…
-20
-10
-8
-5
-4
-8
-12
-16
-20
-10
-8
-5
-4
a
-20
…
(1)通过分析发现,冷柜中的温度y是时间x的函数.
①当4≤x<20时,写出一个符合表中数据的函数解析式;
②当20≤x<24时,写出一个符合表中数据的函数解析式;
(2)求a的值;
(3)如图所示,在直角坐标系中,已描出了上表中部分数据对应的点,请描出剩余数据对应的点,并画出当4≤x≤44时,温度y随时间x变化的函数图象.
知识点四
函数自变量的取值范围
函数自变量的取值范围应使函数表达式有意义.在解决实际问题时,还必须考虑使实际问题有意义.
知识点四
函数自变量的取值范围
函数自变量的取值范围应使函数表达式有意义.在解决实际问题时,还必须考虑使实际问题有意义.
不同类型的函数表达式自变量取值范围的确定:
表达式的类型
自变量的取值范围
整式
全体实数
分式
使分母不为零
二次根式
使被开方数为非负数
零指数幂或负指数幂
使底数不为零
由整式、分式和二次根式等综合得到的代数式
使它们均有意义
知识点四
函数自变量的取值范围
函数自变量的取值范围应使函数表达式有意义.在解决实际问题时,还必须考虑使实际问题有意义.
不同类型的函数表达式自变量取值范围的确定:
求自变量的取值范围关键是明确限制条件,能根据限制条件列方程(组)或不等式(组)求解,或根据实际问题确定自变量的取值范围.
表达式的类型
自变量的取值范围
整式
全体实数
分式
使分母不为零
二次根式
使被开方数为非负数
零指数幂或负指数幂
使底数不为零
由整式、分式和二次根式等综合得到的代数式
使它们均有意义
经典例题
题型
函数表达式的求解与应用
例
有一块矩形地块ABCD,AB=20米,BC=30米为美观,拟种植不同的花卉,如图所示,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形AEHD和BCGF中种植甲种花卉;在等腰梯形ABFE和CDHG中种植乙种花卉;在矩形EFCH中种植丙种花卉.甲,乙,丙三种花卉的种植成本分别为20元/米2,60元/米2,40元/米2,设三种花卉的种植总成本为y元.
(1)当x=5时,求种植总成本y;
(2)求种植总成本y与x的函数表达式,并写出自变量x的
取值范围;
(3)若甲,乙两种花卉的种植面积之差不超过120平方米,
求三种花卉的最低种植总成本.
(2)EF=(20-2x)米,EH=(30-2x)米,
y=(30+30-2x)·x·20+(20+20-2x)·x·60+(30-2x)(20-2x)·40
=-400x+24000(0<x<10).
归纳总结
解决此类题一般需列出函数表达式,再利用函数表达式求值或利用函数的图象、性质解决问题.
第三章
二次函数
1
对函数的再认识
知识点一
函数的定义
一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x在某一范围内的每一个确定值,变量y都有唯一确定的值与它对应,那么我们就称y是x的函数,其中x是自变量,y是因变量.
知识解读
对于函数的定义要把握以下几点:
(1)一个变化过程;
(2)两个变量:自变量是在变化过程中居于主导地位的变量;函数(即因变量)是随之变化的另一个变量;
(3)两变量的对应关系:对于自变量在取值范围内的每一个确定值,因变量都有唯一确定的值与它对应.
具体地,x、y之间的对应关系及是否具有函数关系如下表所示:
(4)函数不是数,它是指某一变化过程中两个变量之间的关系.
x、y之间的对应关系
解释
y是不是x的函数
举例
一一对应
一个x值对应一个y值
是
y=3x+1
多一对应
多个x值对应一个y值
是
y=x2-2
一多对应
一个x值对应多个y值
否
例1
下列图形中,不能代表y是x的函数的是(
)
例1
下列图形中,不能代表y是x的函数的是(
)
解析
观察四个选项,A,B,D三项,对于x的每一个取值,y都有唯一确定的值与之对应;C项中,对于x的每一个取值,y可能有三个值与之对应,不符合函数的定义.
例1
下列图形中,不能代表y是x的函数的是(
C
)
解析
观察四个选项,A,B,D三项,对于x的每一个取值,y都有唯一确定的值与之对应;C项中,对于x的每一个取值,y可能有三个值与之对应,不符合函数的定义.
例1
下列图形中,不能代表y是x的函数的是(
C
)
解析
观察四个选项,A,B,D三项,对于x的每一个取值,y都有唯一确定的值与之对应;C项中,对于x的每一个取值,y可能有三个值与之对应,不符合函数的定义.
归纳总结
判断两变量之间是否存在函数关系,关键是看它们的对应关系.若一个x值对应两个或两个以上的y值,则y不是x的函数.
知识点二
函数值
对于自变量x在某一范围内的一个确定的值a,函数y有唯一确定的对应值,这个对应值叫做当x=a时函数的值简称函数值.
知识点二
函数值
对于自变量x在某一范围内的一个确定的值a,函数y有唯一确定的对应值,这个对应值叫做当x=a时函数的值简称函数值.
温馨提示
(1)当已知函数解析式及自变量的值,欲求函数值时,实质就是求代数式的值.
(2)当已知函数解析式,又给出函数值,欲求相应的自变量的值时,实质就是解方程.
(3)当给定函数值的一个取值范围,欲求相应的自变量的取值范围时,实质就是解不等式.
(4)当自变量确定时,函数值是唯一确定的.但当函数值唯一确定时,对应的自变量可以是多个,如y=x2-1,当y=3时,x=±2.
知识点三
函数的表示方法
用来表示函数关系的数学式子叫做函数的表达式(或解析式),用数学式子表示函数的方法称为解析法.函数还可以用表格和图象表示,分别称为列表法和图象法.
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
列表法
图象法
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
列表法
图象法
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
不直观,有些实际问题不能用解析式表示出来
列表法
图象法
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
不直观,有些实际问题不能用解析式表示出来
列表法
可以清楚、直接地表示出变量之间的数值对应关系
图象法
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
不直观,有些实际问题不能用解析式表示出来
列表法
可以清楚、直接地表示出变量之间的数值对应关系
有局限性,列出的对应值是有限的
图象法
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
不直观,有些实际问题不能用解析式表示出来
列表法
可以清楚、直接地表示出变量之间的数值对应关系
有局限性,列出的对应值是有限的
图象法
可以直观地表示出函数的变化过程和变化趋势
函数的三种表示方法各有优缺点,如下表所示:
?
优点
缺点
解析法
可以准确、完整、简洁地表示出变量之间的关系
不直观,有些实际问题不能用解析式表示出来
列表法
可以清楚、直接地表示出变量之间的数值对应关系
有局限性,列出的对应值是有限的
图象法
可以直观地表示出函数的变化过程和变化趋势
观察得到的自变量或函数的值是近似的
知识拓展
分段函数
定义
在自变量的取值范围内,对于自变量x的不同取值范围、函数与自变量间有不同的对应关系,这样的函数叫做分段函数
定义解读
确定解析式的方法
求值方法
知识拓展
分段函数
定义
在自变量的取值范围内,对于自变量x的不同取值范围、函数与自变量间有不同的对应关系,这样的函数叫做分段函数
定义解读
(1)对分段函数来说,在不同自变量的取值范围内其对应关系不同,但分段函数是一个函数;
(2)分段函数中自变量的取值范围为各段取值范围的并集,分段函数中函数的取值范围为各段函数的取值范围的并集
确定解析式的方法
求值方法
知识拓展
分段函数
定义
在自变量的取值范围内,对于自变量x的不同取值范围、函数与自变量间有不同的对应关系,这样的函数叫做分段函数
定义解读
(1)对分段函数来说,在不同自变量的取值范围内其对应关系不同,但分段函数是一个函数;
(2)分段函数中自变量的取值范围为各段取值范围的并集,分段函数中函数的取值范围为各段函数的取值范围的并集
确定解析式的方法
(1)分别求出自变量在不同范围内的函数解析式;
(2)用“|”表示出各段解析式,注意写明自变量的取值范围
求值方法
知识拓展
分段函数
定义
在自变量的取值范围内,对于自变量x的不同取值范围、函数与自变量间有不同的对应关系,这样的函数叫做分段函数
定义解读
(1)对分段函数来说,在不同自变量的取值范围内其对应关系不同,但分段函数是一个函数;
(2)分段函数中自变量的取值范围为各段取值范围的并集,分段函数中函数的取值范围为各段函数的取值范围的并集
确定解析式的方法
(1)分别求出自变量在不同范围内的函数解析式;
(2)用“|”表示出各段解析式,注意写明自变量的取值范围
求值方法
(1)先确定要求值的自变量属于哪一段;
(2)代入该段的解析式求值
例3
数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度-20℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到-4℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至-20℃时,制冷再次停止,……按照以上方式循环进行.
同学们记录了“44min内15个时间点冷柜中的温度y(℃)随时间x(min)的变化情况”,制成下表:
时间x/min
…
4
8
10
16
20
21
22
23
24
28
30
36
40
42
44
…
温度y/℃
…
-20
-10
-8
-5
-4
-8
-12
-16
-20
-10
-8
-5
-4
a
-20
…
(1)通过分析发现,冷柜中的温度y是时间x的函数.
①当4≤x<20时,写出一个符合表中数据的函数解析式;
②当20≤x<24时,写出一个符合表中数据的函数解析式;
(2)求a的值;
(3)如图所示,在直角坐标系中,已描出了上表中部分数据对应的点,请描出剩余数据对应的点,并画出当4≤x≤44时,温度y随时间x变化的函数图象.
知识点四
函数自变量的取值范围
函数自变量的取值范围应使函数表达式有意义.在解决实际问题时,还必须考虑使实际问题有意义.
知识点四
函数自变量的取值范围
函数自变量的取值范围应使函数表达式有意义.在解决实际问题时,还必须考虑使实际问题有意义.
不同类型的函数表达式自变量取值范围的确定:
表达式的类型
自变量的取值范围
整式
全体实数
分式
使分母不为零
二次根式
使被开方数为非负数
零指数幂或负指数幂
使底数不为零
由整式、分式和二次根式等综合得到的代数式
使它们均有意义
知识点四
函数自变量的取值范围
函数自变量的取值范围应使函数表达式有意义.在解决实际问题时,还必须考虑使实际问题有意义.
不同类型的函数表达式自变量取值范围的确定:
求自变量的取值范围关键是明确限制条件,能根据限制条件列方程(组)或不等式(组)求解,或根据实际问题确定自变量的取值范围.
表达式的类型
自变量的取值范围
整式
全体实数
分式
使分母不为零
二次根式
使被开方数为非负数
零指数幂或负指数幂
使底数不为零
由整式、分式和二次根式等综合得到的代数式
使它们均有意义
经典例题
题型
函数表达式的求解与应用
例
有一块矩形地块ABCD,AB=20米,BC=30米为美观,拟种植不同的花卉,如图所示,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形AEHD和BCGF中种植甲种花卉;在等腰梯形ABFE和CDHG中种植乙种花卉;在矩形EFCH中种植丙种花卉.甲,乙,丙三种花卉的种植成本分别为20元/米2,60元/米2,40元/米2,设三种花卉的种植总成本为y元.
(1)当x=5时,求种植总成本y;
(2)求种植总成本y与x的函数表达式,并写出自变量x的
取值范围;
(3)若甲,乙两种花卉的种植面积之差不超过120平方米,
求三种花卉的最低种植总成本.
(2)EF=(20-2x)米,EH=(30-2x)米,
y=(30+30-2x)·x·20+(20+20-2x)·x·60+(30-2x)(20-2x)·40
=-400x+24000(0<x<10).
归纳总结
解决此类题一般需列出函数表达式,再利用函数表达式求值或利用函数的图象、性质解决问题.
