福建省三明市名校2020-2021学年高二下学期期中考试数学试题( Word版含答案)
文档属性
| 名称 | 福建省三明市名校2020-2021学年高二下学期期中考试数学试题( Word版含答案) | 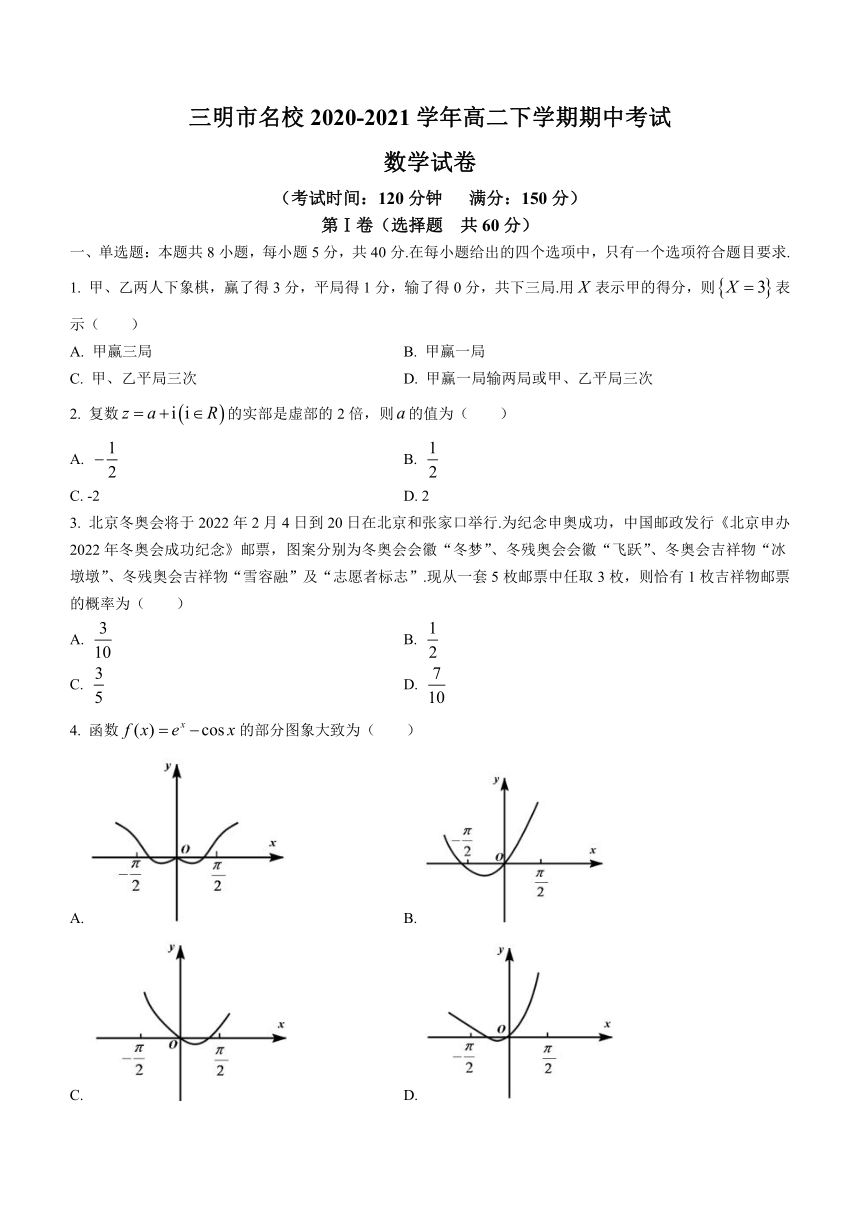 | |
| 格式 | docx | ||
| 文件大小 | 396.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 10:37:48 | ||
图片预览




文档简介
三明市名校2020-2021学年高二下学期期中考试
数学试卷
(考试时间:120分钟
满分:150分)
第Ⅰ卷(选择题
共60分)
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项符合题目要求.
1.
甲、乙两人下象棋,赢了得3分,平局得1分,输了得0分,共下三局.用表示甲的得分,则表示(
)
A.
甲赢三局
B.
甲赢一局
C.
甲、乙平局三次
D.
甲赢一局输两局或甲、乙平局三次
2.
复数的实部是虚部的2倍,则的值为(
)
A.
B.
C.
-2
D.
2
3.
北京冬奥会将于2022年2月4日到20日在北京和张家口举行.为纪念申奥成功,中国邮政发行《北京申办2022年冬奥会成功纪念》邮票,图案分别为冬奥会会徽“冬梦”、冬残奥会会徽“飞跃”、冬奥会吉祥物“冰墩墩”、冬残奥会吉祥物“雪容融”及“志愿者标志”.现从一套5枚邮票中任取3枚,则恰有1枚吉祥物邮票的概率为(
)
A.
B.
C.
D.
4.
函数的部分图象大致为(
)
A.
B.
C.
D.
5.
已知某种产品的合格率是,合格品中的一级品率是.则这种产品的一级品率为(
)
A.
B.
C.
D.
6.
已知函数的单调递增区间是,则(
)
A.
B.
C.
D.
7.
2021年是巩固脱贫攻坚成果的重要一年,某县为响应国家政策,选派了6名工作人员到、、三个村调研脱贫后的产业规划,每个村至少去1人,不同的安排方式共有(
)
A.
480种
B.
540种
C.
600种
D.
630种
8.
原子有稳定和不稳定两种.不稳定的原子除天然元素外,主要由核裂变或核聚变过程中产生碎片形成,这些不稳定的元素在放出、、等射线后,会转变成稳定的原子,这种过程称之为“衰变”.这种不稳定的元素就称为放射性同位素.随着科学技术的发展,放射性同位素技术已经广泛应用于医学、航天等众多领域,并取得了显著经济效益.假设在放射性同位素钍234的衰变过程中,其含量(单位:贝克)与时间(单位:天)满足函数关系,其中为时钍234的含量.已知时,钍234含量的瞬时变化率为,则(
)
A.
12贝克
B.
贝克
C.
6贝克
D.
贝克
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得5分,选对但不全的得3分,有选错的得0分.
9.
下列命题中正确的是(
)
A.
若,,则仅当时为纯虚数
B.
若,互为共轭虚数,则在复平面内它们所对应的点关于轴对称
C.
若,则为纯虚数
D.
若,则
10.
甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8,乙的中靶概率为0.9,则(
)
A.
两人都中靶的概率为0.72
B.
恰好有一人中靶的概率为0.26
C.
两人不都中靶的概率为0.02
D.
至少有一人中靶的概率为0.28
11.
的展开式中(
)
A.
常数项为252
B.
不含的奇次项
C.
偶数项的系数和为-512
D.
系数最大的项为第6项
12.
定义在上的函数满足,,则下列说法正确的是(
)
A.
在处取得极小值,极小值为
B.
只有一个零点
C.
若在上恒成立,则
D.
第Ⅱ卷(非选择题
共90分)
三、填空题:本题共4小题,每小题5分,共20分.
13.
已知,则__________.
14.
若,则__________.
15.
有标号分别为1,2,3,4,5,6的6张防疫宣传海报,要求排成2行3列,则共有___________种不同的排法,如果再要求每列中前面一张的标号比其后面一张的标号小,则共有___________种不同的排法.(结果均用数字作答)
16.
已知函数与的图象上存在两对关于直线对称的点,则实数的取值范围是__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、推理过程或演算步骤.
17.
已知,复数.
(1)若对应的点在第四象限,求的取值范围;
(2)若的共轭复数与复数相等,求的值.
18.
已知函数在处有极值2.
(1)求,的值;
(2)证明:.
19.
某中学将要举行校园歌手大赛,现有4男3女参加,需要安排他们的出场顺序.
(1)如果3个女生都不相邻,那么有多少种不同的出场顺序?
(2)如果女生甲在女生乙的前面(可以不相邻),那么有多少种不同的出场顺序?
(3)如果3位女生都相邻,且女生甲不在第一个出场,那么有多少种不同的出场顺序?(结果均用数字作答)
20.
一个盒子中有10个小球,其中3个红球,7个白球.从这10个球中任取3个.
(1)若采用无放回抽取,求取出的3个球中红球的个数的分布列;
(2)若采用有放回抽取,求取出的3个球中红球的个数的分布列.
21.
已知函数,.
(1)若,求曲线在点处的切线方程;
(2)若在内单调递减,求实数的取值范围.
22.
某工厂购进一批加工设备,由于该设备自动模式运行不稳定,因此一个工作时段内会有的概率出现自动运行故障,此时需要1名维护人员立刻将设备切换至手动操控模式,并持续人工操作至此工作时段结束,期间该人员无法对其它设备进行维护.工厂在每个工作时段开始时将所有设备调至自动模式,若设备的自动模式出现故障而得不到人员的维护,则该设备将停止运行,且每台设备运行的状态相互独立.
(1)若安排1名人员负责维护3台设备,求这3台设备能顺利运行至工作时段结束的概率;
(2)设该工厂有甲,乙两个车间.甲车间有6台设备和2名维护人员,将6台设备平均分配给2人,每名维护人员只负责维护分配给自己的3台设备;乙车间有7台设备和2名维护人员,7台设备由这2人共同负责维护.若用车间所有设备顺利运行至工作时段结束的概率来衡量生产的稳定性,试比较两个车间稳定性的高低.
三明市名校2020-2021学年高二下学期期中考试
数学参考答案
一、单选题
1-5:DDCDA
6-8:CBA
二、多选题
9.
BD
10.
AB
11.
BC
12.
BCD
三、填空题
13.
6
14.
0.096
15.
720;90
16.
四、解答题
17.
解:(1)由复数对应的点在第四象限,
可得,
解得,所以,即的取值范围为.
(2)复数共轭复数为,
因为的共轭复数与复数相等,
所以,
即,解得.
18.
解:(1),,
由已知可得,即,
所以,
经检验符合题意,所以.
(2)设,那么,
令,解得.
当变化时,,的变化情况如下表所示:
1
-
0
+
单调递减
1
单调递增
所以,当时,取得最小值.
所以,即,所以.
19.
解:(1)根据题意,分2步进行分析:
①将4名男生排成一排,有种情况,
②男生排好后有5个空位,在5个空位中任选3个,安排3名女生,有种情况,
故共有种不同的出场顺序.
(2)根据题意,将7人排成一排,有种情况,
其中女生甲在女生乙的前面和女生甲在女生乙的后面的排法是一样的,
故女生甲在女生乙的前面的排法有种不同的出场顺序.
(3)根据题意,分3步进行分析:
①先将3名女生看成一个整体,考虑三人之间的顺序,有种情况,
②将3名女生的整体和4名男生全排列,有种情况,
③女生甲不在第一个出场,减去其第一个出场的情况即可,
则有种符合题意的安排方法.
20.
解:(1)由题意知,随机变量的所有可能取值为0,1,2,3,
且服从参数为,,的超几何分布,
因此,,
所以,,
,;
所以的分布列为:
0
1
2
3
(2)随机变量的所有可能取值为0,1,2,3,且,
所以,
,
,
,
所以的分布列为:
0
1
2
3
0.343
0.441
0.189
0.027
21.
解:(1)因为,所以,
,又因为,
所以曲线在点处的切线方程为,
化简得.
(2)由题可知,其中.
当时,,故在内单调递减;
当时,
对于,,且,所以.
所以当时,.
设,,则
,
所以在上单调递减,
又,.
当时,即时,,对,,所以
,在内单调递增,不符合题意.
当时,即时,,,
所以,使,
因为在内单调递减,所以对,,所以,
所以在内单调递增,不符合题意.
所以当时,在内不单调递减.
综上可得,故的取值范围为.
22.
解:(1)设3台设备自动模式不出故障的台数记为,则,
记“1名人员维护3台设备能顺利运行至工作时段结束”为事件.
则.
(2)甲车间分得的两个小组相互独立,
由(1)知每个小组能保证设备顺利运行至结束概率,
设“甲车间设备顺利运行至结束”为事件,则.
乙车间7台设备自动模式不出故障的台数记为,,
记“乙车间设备顺利运行至结束”为事件,
,
∵,∴,
故乙车间生产稳定性更高.
数学试卷
(考试时间:120分钟
满分:150分)
第Ⅰ卷(选择题
共60分)
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项符合题目要求.
1.
甲、乙两人下象棋,赢了得3分,平局得1分,输了得0分,共下三局.用表示甲的得分,则表示(
)
A.
甲赢三局
B.
甲赢一局
C.
甲、乙平局三次
D.
甲赢一局输两局或甲、乙平局三次
2.
复数的实部是虚部的2倍,则的值为(
)
A.
B.
C.
-2
D.
2
3.
北京冬奥会将于2022年2月4日到20日在北京和张家口举行.为纪念申奥成功,中国邮政发行《北京申办2022年冬奥会成功纪念》邮票,图案分别为冬奥会会徽“冬梦”、冬残奥会会徽“飞跃”、冬奥会吉祥物“冰墩墩”、冬残奥会吉祥物“雪容融”及“志愿者标志”.现从一套5枚邮票中任取3枚,则恰有1枚吉祥物邮票的概率为(
)
A.
B.
C.
D.
4.
函数的部分图象大致为(
)
A.
B.
C.
D.
5.
已知某种产品的合格率是,合格品中的一级品率是.则这种产品的一级品率为(
)
A.
B.
C.
D.
6.
已知函数的单调递增区间是,则(
)
A.
B.
C.
D.
7.
2021年是巩固脱贫攻坚成果的重要一年,某县为响应国家政策,选派了6名工作人员到、、三个村调研脱贫后的产业规划,每个村至少去1人,不同的安排方式共有(
)
A.
480种
B.
540种
C.
600种
D.
630种
8.
原子有稳定和不稳定两种.不稳定的原子除天然元素外,主要由核裂变或核聚变过程中产生碎片形成,这些不稳定的元素在放出、、等射线后,会转变成稳定的原子,这种过程称之为“衰变”.这种不稳定的元素就称为放射性同位素.随着科学技术的发展,放射性同位素技术已经广泛应用于医学、航天等众多领域,并取得了显著经济效益.假设在放射性同位素钍234的衰变过程中,其含量(单位:贝克)与时间(单位:天)满足函数关系,其中为时钍234的含量.已知时,钍234含量的瞬时变化率为,则(
)
A.
12贝克
B.
贝克
C.
6贝克
D.
贝克
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得5分,选对但不全的得3分,有选错的得0分.
9.
下列命题中正确的是(
)
A.
若,,则仅当时为纯虚数
B.
若,互为共轭虚数,则在复平面内它们所对应的点关于轴对称
C.
若,则为纯虚数
D.
若,则
10.
甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8,乙的中靶概率为0.9,则(
)
A.
两人都中靶的概率为0.72
B.
恰好有一人中靶的概率为0.26
C.
两人不都中靶的概率为0.02
D.
至少有一人中靶的概率为0.28
11.
的展开式中(
)
A.
常数项为252
B.
不含的奇次项
C.
偶数项的系数和为-512
D.
系数最大的项为第6项
12.
定义在上的函数满足,,则下列说法正确的是(
)
A.
在处取得极小值,极小值为
B.
只有一个零点
C.
若在上恒成立,则
D.
第Ⅱ卷(非选择题
共90分)
三、填空题:本题共4小题,每小题5分,共20分.
13.
已知,则__________.
14.
若,则__________.
15.
有标号分别为1,2,3,4,5,6的6张防疫宣传海报,要求排成2行3列,则共有___________种不同的排法,如果再要求每列中前面一张的标号比其后面一张的标号小,则共有___________种不同的排法.(结果均用数字作答)
16.
已知函数与的图象上存在两对关于直线对称的点,则实数的取值范围是__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、推理过程或演算步骤.
17.
已知,复数.
(1)若对应的点在第四象限,求的取值范围;
(2)若的共轭复数与复数相等,求的值.
18.
已知函数在处有极值2.
(1)求,的值;
(2)证明:.
19.
某中学将要举行校园歌手大赛,现有4男3女参加,需要安排他们的出场顺序.
(1)如果3个女生都不相邻,那么有多少种不同的出场顺序?
(2)如果女生甲在女生乙的前面(可以不相邻),那么有多少种不同的出场顺序?
(3)如果3位女生都相邻,且女生甲不在第一个出场,那么有多少种不同的出场顺序?(结果均用数字作答)
20.
一个盒子中有10个小球,其中3个红球,7个白球.从这10个球中任取3个.
(1)若采用无放回抽取,求取出的3个球中红球的个数的分布列;
(2)若采用有放回抽取,求取出的3个球中红球的个数的分布列.
21.
已知函数,.
(1)若,求曲线在点处的切线方程;
(2)若在内单调递减,求实数的取值范围.
22.
某工厂购进一批加工设备,由于该设备自动模式运行不稳定,因此一个工作时段内会有的概率出现自动运行故障,此时需要1名维护人员立刻将设备切换至手动操控模式,并持续人工操作至此工作时段结束,期间该人员无法对其它设备进行维护.工厂在每个工作时段开始时将所有设备调至自动模式,若设备的自动模式出现故障而得不到人员的维护,则该设备将停止运行,且每台设备运行的状态相互独立.
(1)若安排1名人员负责维护3台设备,求这3台设备能顺利运行至工作时段结束的概率;
(2)设该工厂有甲,乙两个车间.甲车间有6台设备和2名维护人员,将6台设备平均分配给2人,每名维护人员只负责维护分配给自己的3台设备;乙车间有7台设备和2名维护人员,7台设备由这2人共同负责维护.若用车间所有设备顺利运行至工作时段结束的概率来衡量生产的稳定性,试比较两个车间稳定性的高低.
三明市名校2020-2021学年高二下学期期中考试
数学参考答案
一、单选题
1-5:DDCDA
6-8:CBA
二、多选题
9.
BD
10.
AB
11.
BC
12.
BCD
三、填空题
13.
6
14.
0.096
15.
720;90
16.
四、解答题
17.
解:(1)由复数对应的点在第四象限,
可得,
解得,所以,即的取值范围为.
(2)复数共轭复数为,
因为的共轭复数与复数相等,
所以,
即,解得.
18.
解:(1),,
由已知可得,即,
所以,
经检验符合题意,所以.
(2)设,那么,
令,解得.
当变化时,,的变化情况如下表所示:
1
-
0
+
单调递减
1
单调递增
所以,当时,取得最小值.
所以,即,所以.
19.
解:(1)根据题意,分2步进行分析:
①将4名男生排成一排,有种情况,
②男生排好后有5个空位,在5个空位中任选3个,安排3名女生,有种情况,
故共有种不同的出场顺序.
(2)根据题意,将7人排成一排,有种情况,
其中女生甲在女生乙的前面和女生甲在女生乙的后面的排法是一样的,
故女生甲在女生乙的前面的排法有种不同的出场顺序.
(3)根据题意,分3步进行分析:
①先将3名女生看成一个整体,考虑三人之间的顺序,有种情况,
②将3名女生的整体和4名男生全排列,有种情况,
③女生甲不在第一个出场,减去其第一个出场的情况即可,
则有种符合题意的安排方法.
20.
解:(1)由题意知,随机变量的所有可能取值为0,1,2,3,
且服从参数为,,的超几何分布,
因此,,
所以,,
,;
所以的分布列为:
0
1
2
3
(2)随机变量的所有可能取值为0,1,2,3,且,
所以,
,
,
,
所以的分布列为:
0
1
2
3
0.343
0.441
0.189
0.027
21.
解:(1)因为,所以,
,又因为,
所以曲线在点处的切线方程为,
化简得.
(2)由题可知,其中.
当时,,故在内单调递减;
当时,
对于,,且,所以.
所以当时,.
设,,则
,
所以在上单调递减,
又,.
当时,即时,,对,,所以
,在内单调递增,不符合题意.
当时,即时,,,
所以,使,
因为在内单调递减,所以对,,所以,
所以在内单调递增,不符合题意.
所以当时,在内不单调递减.
综上可得,故的取值范围为.
22.
解:(1)设3台设备自动模式不出故障的台数记为,则,
记“1名人员维护3台设备能顺利运行至工作时段结束”为事件.
则.
(2)甲车间分得的两个小组相互独立,
由(1)知每个小组能保证设备顺利运行至结束概率,
设“甲车间设备顺利运行至结束”为事件,则.
乙车间7台设备自动模式不出故障的台数记为,,
记“乙车间设备顺利运行至结束”为事件,
,
∵,∴,
故乙车间生产稳定性更高.
同课章节目录
