云南省马关一高2020-2021学年高二下学期期末考试数学试题( Word版,含答案)
文档属性
| 名称 | 云南省马关一高2020-2021学年高二下学期期末考试数学试题( Word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 349.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 00:00:00 | ||
图片预览



文档简介
马关一高2020-2021学年高二下学期数学期末试卷
一、单选题
1.设a>0,b>0,则以下不等式中,不恒成立的是( )
A.??????????????B.??????????????
C.??????????????D.?aabb>abba
2.已知抛物线上存在关于直线x+y=0对称的相异两点A,B,则等于(???)
A.?3????????????????????????????????????????B.?4????????????????????????????????????????C.?????????????????????????????????????????D.?
3.已知等比数列的首项公比,
则(??
)
A.?50?????????????????????????????????????????B.?35?????????????????????????????????????????C.?55?????????????????????????????????????????D.?46
4.如图,在正方体ABCD﹣A1B1C1D1中,异面直线A1D与D1C所成的角为(??
)
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?60°???????????????????????????????????????D.?90°
5.下列说法正确的是(??
)
A.?命题“若
,则
”的否命题为“若
,则
”;
B.?命题“
”的否定是“
”;
C.?命题“若x=y,则
”的逆否命题为真命题;
D.?“
”
是“
”的必要不充分条件.
6.设Sn为等比数列{an}的前n项和,若,
则(???
)
A.?-8??????????????????????????????????????????B.?5??????????????????????????????????????????C.?8??????????????????????????????????????????D.?15
7.设等比数列{an}的前
n
项和为Sn
,
且S3=7a1
,则数列{an}的公比q的值为(??
)
A.?2或-3???????????????????????????????????????B.?2或3???????????????????????????????????????C.?2???????????????????????????????????????D.?3
8.定义方程
的实根
叫做函数
的“新驻点”,若函数
,
,
的“新驻点”分别为
,
,
,则
,
,
的大小关系为(???
)
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
9.椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的两倍,则m的值为( )
A.? ??????????????????????????????????????B.???????????????????????????????????????C.?2 ??????????????????????????????????????D.?4
10.已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为(2,0),则|
|的最大值为(??
)
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
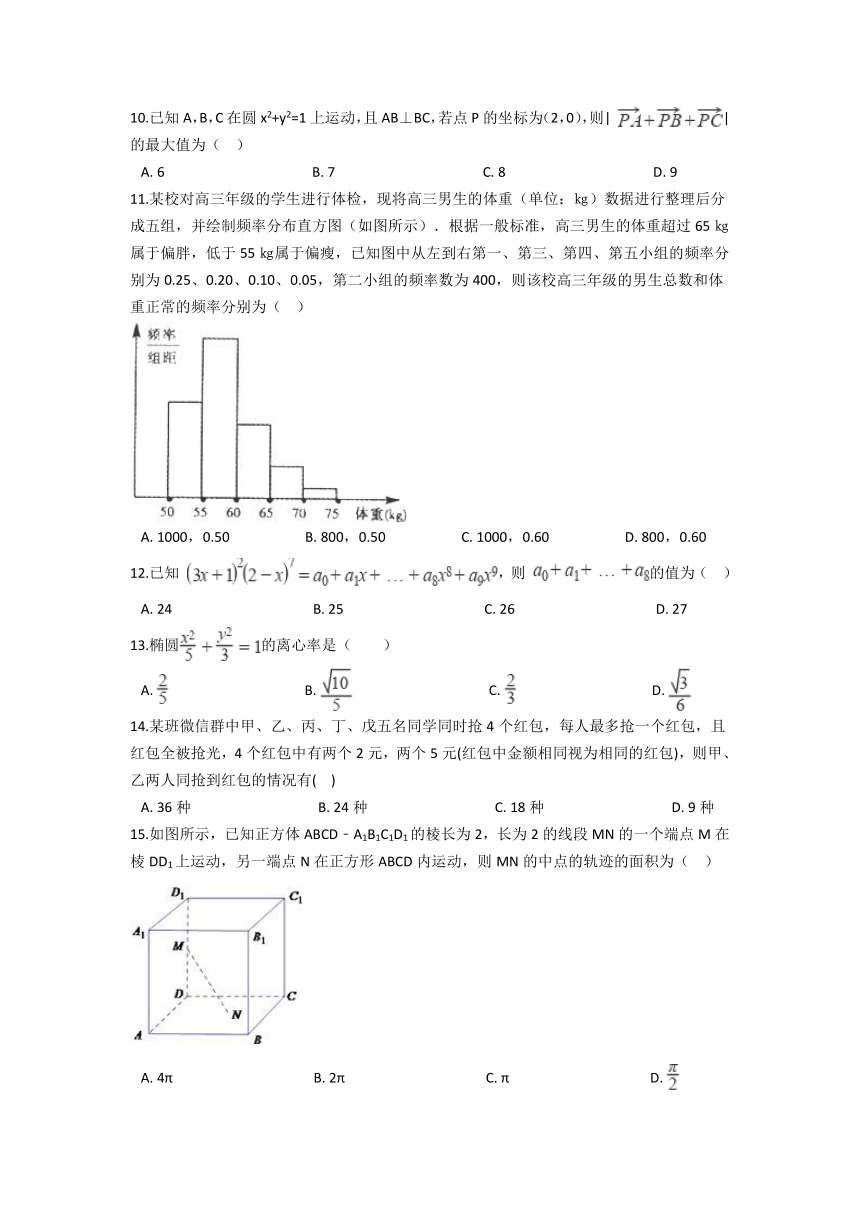
11.某校对高三年级的学生进行体检,现将高三男生的体重(单位:㎏)数据进行整理后分成五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65㎏属于偏胖,低于55㎏属于偏瘦,已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频率数为400,则该校高三年级的男生总数和体重正常的频率分别为(??
)
A.?1000,0.50??????????????????????B.?800,0.50??????????????????????C.?1000,0.60??????????????????????D.?800,0.60
12.已知
,则
的值为(??
)
A.?24?????????????????????????????????????????B.?25?????????????????????????????????????????C.?26?????????????????????????????????????????D.?27
13.椭圆的离心率是( )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
14.某班微信群中甲、乙、丙、丁、戊五名同学同时抢4个红包,每人最多抢一个红包,且红包全被抢光,4个红包中有两个2元,两个5元(红包中金额相同视为相同的红包),则甲、乙两人同抢到红包的情况有(??
)
A.?36种?????????????????????????????????????B.?24种?????????????????????????????????????C.?18种?????????????????????????????????????D.?9种
15.如图所示,已知正方体ABCD﹣A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为(??
)
A.?4π?????????????????????????????????????????B.?2π?????????????????????????????????????????C.?π?????????????????????????????????????????D.?
16.在平面直角坐标系中,不等式组表示的平面区域的面积是??
(
)
A.?????????????????????????????????????????B.?4????????????????????????????????????????C.?????????????????????????????????????????D.?2
17.设函数,
则等于(??
)
A.0
B.60
C.-1
D.-60
18.在等比数列{an}中,a1=2,前n项和为sn
,
若数列{an+1}也是等比数列,则sn等于(?
)
A.?2n+1﹣2???????????????????????????????????B.?3n2???????????????????????????????????C.?2n???????????????????????????????????D.?3n﹣1
19.已知函数y=f(x)的定义域为R,满足且函数y=f(x+2)为偶函数,,
则实数a,b,c的大小关系是(???)
A.?a>B>c???????????????????????????????B.?c>b>a???????????????????????????????C.?b>c>a???????????????????????????????D.?c>a>b
20.已知函数
有两个零点,则
的取值范围是(?
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
二、填空题
21.在△ABC中,如果0<tanAtanB<1,那么△ABC是________三角形.(填“钝角”、“锐角”、“直角”)
22.在三角形ABC中,已知A=60°,b=1,其面积为
,则
=________.
23.若有三个新冠肺炎重症突击小分队,已知第一小分队人数多于第二小分队,第二小分队人数多于第三小分队,但第三小分队人数的两倍却要多于第一小分队.则这三个小分队人数的总和的最小值为________.
24.与双曲线
﹣y2=1有相同渐近线,且与椭圆
=1有共同焦点的双曲线方程是________.
25.已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈[
,2]时,函数f(x)=x+
>
恒成立.如果“p或q”为真命题,“p且q”为假命题,则c的取值范围是________.
26.在
的内角
,
,
的对边分别为
,
,
,已知
,则
的值为________.
27.如图所示,终边落在直线y=
x上的角的集合为________.
28.如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北的方向上,行驶600m后到达B处,测得此山顶在西偏北的方向上,仰角为,
则此山的高度________
m.
?
?
29.4张卡片的正、反面分别写有0与1,2与3,4与5,6与7,将其中3张卡片排放在一起,可组成________个不同的三位数.
30.对于函数f(x)=
给出下列四个命题:
①该函数是以π为最小正周期的周期函数;
②当且仅当x=π+2kπ(k∈Z)时,该函数取得最小值﹣1;
③该函数的图象关于x=
+2kπ(k∈Z)对称;
④当且仅当2kπ<x<
+2kπ(k∈Z)时,0<f(x)≤
其中正确命题的序号是________.(请将所有正确命题的序号都填上)
三、解答题
31.已知函数
(
是自然对数的底数).
(1)求证:
;
(2)若不等式
在
上恒成立,求正实数
的取值范围.
32.已知
.
(1)当
时,求不等式
的解集;
(2)若
,对
恒成立,求实数
的取值范围.
33.?????????????????????
??
(1)椭圆的焦点为
,点
是椭圆上的一个点,求椭圆的方程.
(2)求以椭圆
+
=1的焦点为焦点,一条渐近线方程为y=-
x的双曲线方程.
34.如图,设F1
,
F2是椭圆C:
(a>b>0)的左、右焦点,直线y=kx(k>0)与椭圆C交于A,B.已知椭圆C的焦距是2,四边形AF1BF2的周长是4
.
(1)求椭圆C的方程;
(2)直线AF1
,
BF1分别与椭圆C交于M,N,求△MNF1面积的最大值.
35.如图,在三棱柱
中,
、
分别为
、
的中点,
,
,
.
(1)求证:
平面
;
(2)求二面角
的余弦值.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
C
3.【答案】
C
4.【答案】
C
5.【答案】
C
6.【答案】
B
7.【答案】
A
8.【答案】
B
9.【答案】
A
10.【答案】
B
11.【答案】
C
12.【答案】
B
13.【答案】
B
14.【答案】
C
15.【答案】
D
16.【答案】
B
17.【答案】
B
18.【答案】
C
19.【答案】
B
20.【答案】
B
二、填空题
21.【答案】
钝角
22.【答案】
23.【答案】
12
24.【答案】
﹣
=1
25.【答案】
26.【答案】
27.【答案】
{α|α=60°+n?180°,n∈Z}
28.【答案】
29.【答案】
168
30.【答案】③④
三、解答题
31.【答案】
(1)证明:
,可得
,
当
,解得
,
∴当
时,
为增函数,
当
时,
为减函数,
的最小值为
.
(2)证明:∵不等式
在
上恒成立,
在
上恒成立,
即
在
上恒成立.
令
,
,当
时,解得
,
∴当
时,
为减函数,
当
时,
为增函数,
的最小值为
,
∴
,
则正数
的取值范围为
32.【答案】
(1)解:
时,即求解
,
①当
时,
,∴
;
②当
时,
,∴
,无解;
③当
时,
,∴
.综上,解集为
(2)解:即
恒成立,令
则函数图象如图:
∴
,∴
33.【答案】
(1)解:依题意可知椭圆
,且焦点在
轴上,设椭圆方程为
,将点
的坐标代入椭圆方程得
,结合
,解得
.故所求椭圆方程为
.
(2)解:依题意可知椭圆的焦点为
,故双曲线
,根据双曲线的渐近线方程可知
,结合
,觉得
,故双曲线方程为
.
34.【答案】
(1)解:由题意可得2c=2,4a=4
,b2=a2﹣c2
,
解得:a2=2,b2=1,
∴椭圆的方程为:
=1.
(2)解:设A(x0
,
y0),(x0>0,y0>0),B(﹣x0
,
﹣y0),
则直线AF1:
,直线BF1:
联立
,得
,
又
=1,代入化简得
=0,
∴y0yM=﹣
,∴
,∴
=﹣
,
同理得
,xN=
,设直线MN与x轴交于E(t,0),
由M,N,E三点共线得kME=kNE
,
得t=﹣
,
∴
=
=
=
≤
,当
时,取等号.
∴△MNF1面积的最大值为
。
35.【答案】
(1)证明:连接
.
∵
,
为
的中点,∴
.
∵
,
,∴
.
∵
,
为
的中点,∴
.
∵
,
,∴
.
∵
,故
,∴
.
∵
,
,∴
平面
(2)解:以
为坐标原点,
,
,
所在的直线分别为
,
,
轴,
建立如图所示的空间直角坐标系.
则
,
,
.
则
,
.
设平面
的法向量
,
则
.
令
,则
,
,则
.
易证
平面
,故取平面
的法向量
.
.
因为二面角
的平面角
为锐角,所以
一、单选题
1.设a>0,b>0,则以下不等式中,不恒成立的是( )
A.??????????????B.??????????????
C.??????????????D.?aabb>abba
2.已知抛物线上存在关于直线x+y=0对称的相异两点A,B,则等于(???)
A.?3????????????????????????????????????????B.?4????????????????????????????????????????C.?????????????????????????????????????????D.?
3.已知等比数列的首项公比,
则(??
)
A.?50?????????????????????????????????????????B.?35?????????????????????????????????????????C.?55?????????????????????????????????????????D.?46
4.如图,在正方体ABCD﹣A1B1C1D1中,异面直线A1D与D1C所成的角为(??
)
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?60°???????????????????????????????????????D.?90°
5.下列说法正确的是(??
)
A.?命题“若
,则
”的否命题为“若
,则
”;
B.?命题“
”的否定是“
”;
C.?命题“若x=y,则
”的逆否命题为真命题;
D.?“
”
是“
”的必要不充分条件.
6.设Sn为等比数列{an}的前n项和,若,
则(???
)
A.?-8??????????????????????????????????????????B.?5??????????????????????????????????????????C.?8??????????????????????????????????????????D.?15
7.设等比数列{an}的前
n
项和为Sn
,
且S3=7a1
,则数列{an}的公比q的值为(??
)
A.?2或-3???????????????????????????????????????B.?2或3???????????????????????????????????????C.?2???????????????????????????????????????D.?3
8.定义方程
的实根
叫做函数
的“新驻点”,若函数
,
,
的“新驻点”分别为
,
,
,则
,
,
的大小关系为(???
)
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
9.椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的两倍,则m的值为( )
A.? ??????????????????????????????????????B.???????????????????????????????????????C.?2 ??????????????????????????????????????D.?4
10.已知A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为(2,0),则|
|的最大值为(??
)
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
11.某校对高三年级的学生进行体检,现将高三男生的体重(单位:㎏)数据进行整理后分成五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65㎏属于偏胖,低于55㎏属于偏瘦,已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频率数为400,则该校高三年级的男生总数和体重正常的频率分别为(??
)
A.?1000,0.50??????????????????????B.?800,0.50??????????????????????C.?1000,0.60??????????????????????D.?800,0.60
12.已知
,则
的值为(??
)
A.?24?????????????????????????????????????????B.?25?????????????????????????????????????????C.?26?????????????????????????????????????????D.?27
13.椭圆的离心率是( )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
14.某班微信群中甲、乙、丙、丁、戊五名同学同时抢4个红包,每人最多抢一个红包,且红包全被抢光,4个红包中有两个2元,两个5元(红包中金额相同视为相同的红包),则甲、乙两人同抢到红包的情况有(??
)
A.?36种?????????????????????????????????????B.?24种?????????????????????????????????????C.?18种?????????????????????????????????????D.?9种
15.如图所示,已知正方体ABCD﹣A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为(??
)
A.?4π?????????????????????????????????????????B.?2π?????????????????????????????????????????C.?π?????????????????????????????????????????D.?
16.在平面直角坐标系中,不等式组表示的平面区域的面积是??
(
)
A.?????????????????????????????????????????B.?4????????????????????????????????????????C.?????????????????????????????????????????D.?2
17.设函数,
则等于(??
)
A.0
B.60
C.-1
D.-60
18.在等比数列{an}中,a1=2,前n项和为sn
,
若数列{an+1}也是等比数列,则sn等于(?
)
A.?2n+1﹣2???????????????????????????????????B.?3n2???????????????????????????????????C.?2n???????????????????????????????????D.?3n﹣1
19.已知函数y=f(x)的定义域为R,满足且函数y=f(x+2)为偶函数,,
则实数a,b,c的大小关系是(???)
A.?a>B>c???????????????????????????????B.?c>b>a???????????????????????????????C.?b>c>a???????????????????????????????D.?c>a>b
20.已知函数
有两个零点,则
的取值范围是(?
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
二、填空题
21.在△ABC中,如果0<tanAtanB<1,那么△ABC是________三角形.(填“钝角”、“锐角”、“直角”)
22.在三角形ABC中,已知A=60°,b=1,其面积为
,则
=________.
23.若有三个新冠肺炎重症突击小分队,已知第一小分队人数多于第二小分队,第二小分队人数多于第三小分队,但第三小分队人数的两倍却要多于第一小分队.则这三个小分队人数的总和的最小值为________.
24.与双曲线
﹣y2=1有相同渐近线,且与椭圆
=1有共同焦点的双曲线方程是________.
25.已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈[
,2]时,函数f(x)=x+
>
恒成立.如果“p或q”为真命题,“p且q”为假命题,则c的取值范围是________.
26.在
的内角
,
,
的对边分别为
,
,
,已知
,则
的值为________.
27.如图所示,终边落在直线y=
x上的角的集合为________.
28.如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北的方向上,行驶600m后到达B处,测得此山顶在西偏北的方向上,仰角为,
则此山的高度________
m.
?
?
29.4张卡片的正、反面分别写有0与1,2与3,4与5,6与7,将其中3张卡片排放在一起,可组成________个不同的三位数.
30.对于函数f(x)=
给出下列四个命题:
①该函数是以π为最小正周期的周期函数;
②当且仅当x=π+2kπ(k∈Z)时,该函数取得最小值﹣1;
③该函数的图象关于x=
+2kπ(k∈Z)对称;
④当且仅当2kπ<x<
+2kπ(k∈Z)时,0<f(x)≤
其中正确命题的序号是________.(请将所有正确命题的序号都填上)
三、解答题
31.已知函数
(
是自然对数的底数).
(1)求证:
;
(2)若不等式
在
上恒成立,求正实数
的取值范围.
32.已知
.
(1)当
时,求不等式
的解集;
(2)若
,对
恒成立,求实数
的取值范围.
33.?????????????????????
??
(1)椭圆的焦点为
,点
是椭圆上的一个点,求椭圆的方程.
(2)求以椭圆
+
=1的焦点为焦点,一条渐近线方程为y=-
x的双曲线方程.
34.如图,设F1
,
F2是椭圆C:
(a>b>0)的左、右焦点,直线y=kx(k>0)与椭圆C交于A,B.已知椭圆C的焦距是2,四边形AF1BF2的周长是4
.
(1)求椭圆C的方程;
(2)直线AF1
,
BF1分别与椭圆C交于M,N,求△MNF1面积的最大值.
35.如图,在三棱柱
中,
、
分别为
、
的中点,
,
,
.
(1)求证:
平面
;
(2)求二面角
的余弦值.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
C
3.【答案】
C
4.【答案】
C
5.【答案】
C
6.【答案】
B
7.【答案】
A
8.【答案】
B
9.【答案】
A
10.【答案】
B
11.【答案】
C
12.【答案】
B
13.【答案】
B
14.【答案】
C
15.【答案】
D
16.【答案】
B
17.【答案】
B
18.【答案】
C
19.【答案】
B
20.【答案】
B
二、填空题
21.【答案】
钝角
22.【答案】
23.【答案】
12
24.【答案】
﹣
=1
25.【答案】
26.【答案】
27.【答案】
{α|α=60°+n?180°,n∈Z}
28.【答案】
29.【答案】
168
30.【答案】③④
三、解答题
31.【答案】
(1)证明:
,可得
,
当
,解得
,
∴当
时,
为增函数,
当
时,
为减函数,
的最小值为
.
(2)证明:∵不等式
在
上恒成立,
在
上恒成立,
即
在
上恒成立.
令
,
,当
时,解得
,
∴当
时,
为减函数,
当
时,
为增函数,
的最小值为
,
∴
,
则正数
的取值范围为
32.【答案】
(1)解:
时,即求解
,
①当
时,
,∴
;
②当
时,
,∴
,无解;
③当
时,
,∴
.综上,解集为
(2)解:即
恒成立,令
则函数图象如图:
∴
,∴
33.【答案】
(1)解:依题意可知椭圆
,且焦点在
轴上,设椭圆方程为
,将点
的坐标代入椭圆方程得
,结合
,解得
.故所求椭圆方程为
.
(2)解:依题意可知椭圆的焦点为
,故双曲线
,根据双曲线的渐近线方程可知
,结合
,觉得
,故双曲线方程为
.
34.【答案】
(1)解:由题意可得2c=2,4a=4
,b2=a2﹣c2
,
解得:a2=2,b2=1,
∴椭圆的方程为:
=1.
(2)解:设A(x0
,
y0),(x0>0,y0>0),B(﹣x0
,
﹣y0),
则直线AF1:
,直线BF1:
联立
,得
,
又
=1,代入化简得
=0,
∴y0yM=﹣
,∴
,∴
=﹣
,
同理得
,xN=
,设直线MN与x轴交于E(t,0),
由M,N,E三点共线得kME=kNE
,
得t=﹣
,
∴
=
=
=
≤
,当
时,取等号.
∴△MNF1面积的最大值为
。
35.【答案】
(1)证明:连接
.
∵
,
为
的中点,∴
.
∵
,
,∴
.
∵
,
为
的中点,∴
.
∵
,
,∴
.
∵
,故
,∴
.
∵
,
,∴
平面
(2)解:以
为坐标原点,
,
,
所在的直线分别为
,
,
轴,
建立如图所示的空间直角坐标系.
则
,
,
.
则
,
.
设平面
的法向量
,
则
.
令
,则
,
,则
.
易证
平面
,故取平面
的法向量
.
.
因为二面角
的平面角
为锐角,所以
同课章节目录
