云南省马关一高2020-2021学年高一下学期期末考试数学试题 (Word版,含答案)
文档属性
| 名称 | 云南省马关一高2020-2021学年高一下学期期末考试数学试题 (Word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 317.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 00:00:00 | ||
图片预览


文档简介
马关一高2020-2021学年高一下学期数学期末试卷
一、单选题
1.对任意的实数
,在下列命题中的真命题是(
??)
A.?“
”是“
”的必要不充分条件?????B.?“
”是“
”的必要不充分条件
C.?“
”是“
”的充分不必要条件?????D.?“
”是“
”的充分不必要条件
2.口袋内装有一些大小相同的红球、白球和黒球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0.28,那么摸出黒球的概率是( )
A.?0.42??????????????????????????????????????B.?0.28??????????????????????????????????????C.?0.3???????????????????????????????????????D.?0.7
3.已知
是等差数列,且
,则
的值是(???
)
A.??
24????????????????????????????????????????B.?27????????????????????????????????????????C.?30????????????????????????????????????????D.?33
4.如图,网格纸上小正方形变长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体体积为(??
)
A.??????????????????????????????????????B.???
B.?????????????????????????????????????C.?8?????????????????????????????????????D.?
5.已知偶函数f(x)在(0,+∞)上单调递增,则f(﹣3),f(﹣1),f(2)的大小关系是(?
)
A.?f(2)>f(﹣3)>f(﹣1)??????????????????????????????B.?f(﹣1)>f(2)>f(﹣3)
C.?f(﹣3)>f(﹣1)>f(2)??????????????????????????????D.?f(﹣3)>f(2)>f(﹣1)
6.已知函数,
则下列等式对恒成立的是(???)
A.f(-x)=f(x)
B.
C.
D.f(-x)=-sinx
7.设m,n表示不同的直线,α,β表示不同的平面,且m,n?α.则“α∥β”是“m∥β且n∥β”的( )
A.?充分但不必要条件???????????B.?必要但不充分条件???????????C.?充要条件???????????D.?既不充分又不必要条件
8.已知A=
,则a=(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?0???????????????????????????????????????????D.?
9.下列函数中,既是偶函数,又在区间(0,3)内是减函数的是(??
)
A.?y=2x﹣2﹣x??????????????????????????B.?y=cosx??????????????????????????C.?y=log2|x|??????????????????????????D.?y=x+x﹣1
10.在区间(0,3]上随机取一个数x,则事件“0≤log2x≤1”发生的概率为(??
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
11.已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.则该几何体的体积为(???
)
A.?48????????????????????????????????????????B.?64????????????????????????????????????????C.?96????????????????????????????????????????D.?192
12.已知函数
则函数y=f[f(x)]+1的零点个数是(?
)
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????C.?2???????????????????????????????????????????D.?1
13.已知函数
+2,则关于x的不等式f(3x+1)+f(x)>4的解集为(??
)
A.?(﹣
,+∞)???????????B.?(﹣
,+∞)???????????C.?(﹣
,+∞)???????????D.?(﹣
,+∞)
14.已知实数a1
,
a2
,
b1
,
b2
,
b3满足数列1,a1
,
a2
,
9是等差数列,数列1,b1
,
b2
,
b3
,
9是等比数列,则
的值为(??
)
A.?±
?????????????????????????????????????B.??????????????????????????????????????C.?﹣
?????????????????????????????????????D.?1
15.已知f(x)=,
则f()的值是( )
A.?0??????????????????????????????????????????B.?1??????????????????????????????????????????C.???????????????????????????????????????????D.?-
16.直线3x﹣4y﹣9=0被圆(x﹣3)2+y2=9截得的弦长为(??
)
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
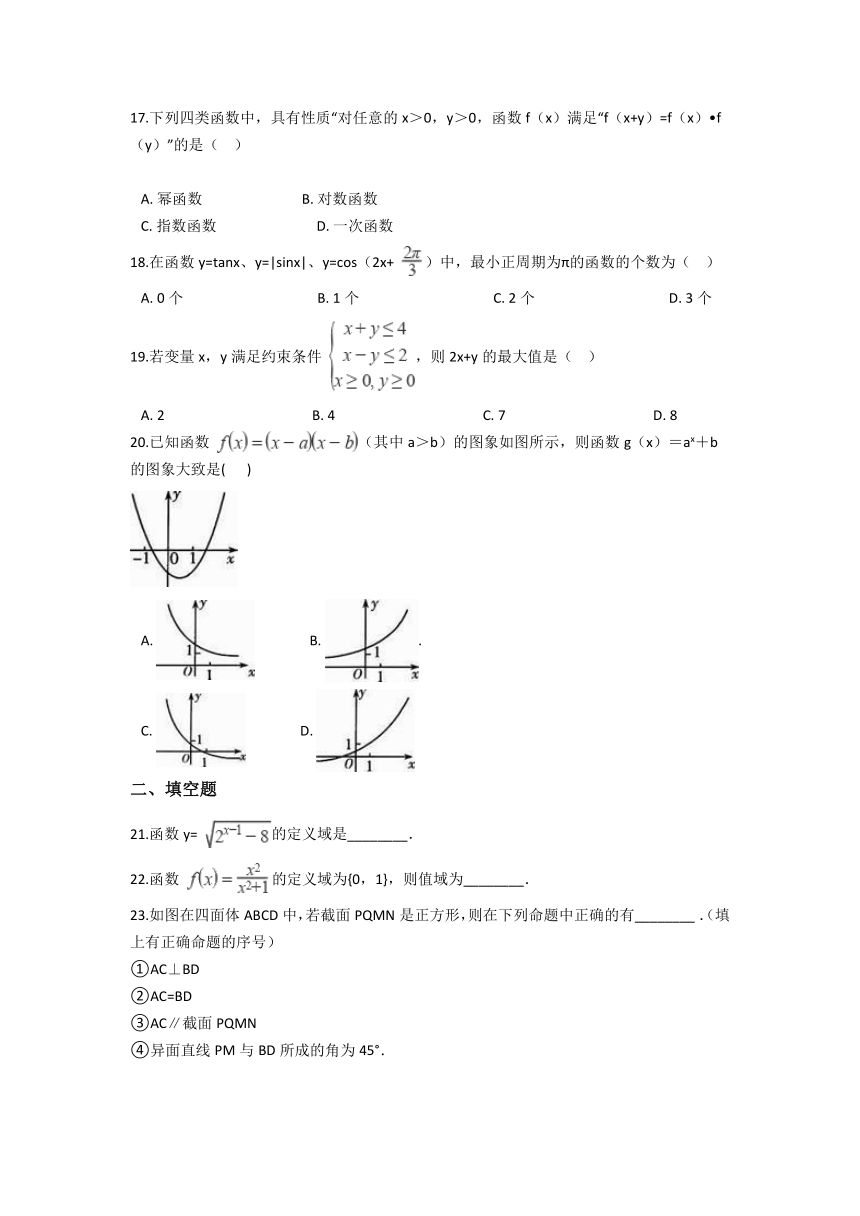
17.下列四类函数中,具有性质“对任意的x>0,y>0,函数f(x)满足“f(x+y)=f(x)?f(y)”的是(??
)
A.?幂函数?????????????????????????????B.?对数函数?????????????????????????????
C.?指数函数?????????????????????????????D.?一次函数
18.在函数y=tanx、y=|sinx|、y=cos(2x+
)中,最小正周期为π的函数的个数为(??
)
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
19.若变量x,y满足约束条件
,则2x+y的最大值是(??
)
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
20.已知函数
(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象大致是(????
)
A.?????????????????B.?.????????????????
C.?????????????????D.?
二、填空题
21.函数y=
的定义域是________.
22.函数
的定义域为{0,1},则值域为________.
23.如图在四面体ABCD中,若截面PQMN是正方形,则在下列命题中正确的有________?.(填上有正确命题的序号)
①AC⊥BD
②AC=BD
③AC∥截面PQMN
④异面直线PM与BD所成的角为45°.
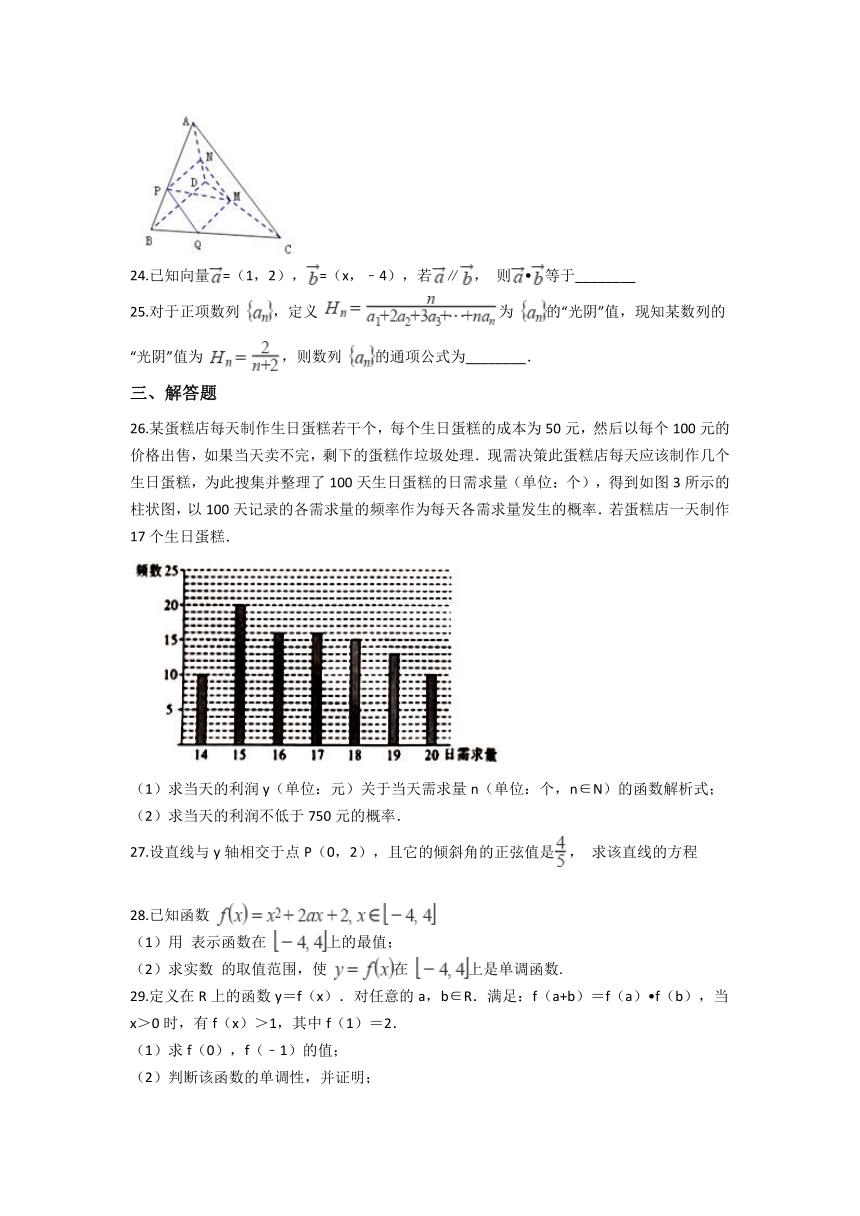
24.已知向量=(1,2),=(x,﹣4),若∥,
则?等于________?
25.对于正项数列
,定义
为
的“光阴”值,现知某数列的“光阴”值为
,则数列
的通项公式为________.
三、解答题
26.某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图3所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.若蛋糕店一天制作17个生日蛋糕.
(1)求当天的利润y(单位:元)关于当天需求量n(单位:个,n∈N)的函数解析式;
(2)求当天的利润不低于750元的概率.
27.设直线与y轴相交于点P(0,2),且它的倾斜角的正弦值是,
求该直线的方程
28.已知函数
(1)用
表示函数在
上的最值;
(2)求实数
的取值范围,使
在
上是单调函数.
29.定义在R上的函数y=f(x).对任意的a,b∈R.满足:f(a+b)=f(a)?f(b),当x>0时,有f(x)>1,其中f(1)=2.
(1)求f(0),f(﹣1)的值;
(2)判断该函数的单调性,并证明;
(3)求不等式f(x+1)<4的解集.
30.已知函数:
且
.
(1)证明:
对定义域内的所有
都成立;
(2)当
的定义域为
时,求证:
的值域为
;
(3)设函数
,求
的最小值.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
C
3.【答案】
D
4.【答案】A
5.【答案】
D
6.【答案】
C
7.【答案】
A
8.【答案】
B
9.【答案】B
10.【答案】
C
11.【答案】
B
12.【答案】
A
13.【答案】
D
14.【答案】B
15.【答案】
C
16.【答案】
D
17.【答案】
C
18.【答案】D
19.【答案】
C
20.【答案】
D
二、填空题
21.【答案】[4,+∞)
22.【答案】{0,
}
23.【答案】
①③④
24.【答案】
-10
25.【答案】
三、解答题
26.【答案】
(1)解:当n≥17时,y=17×(100﹣50)=850;
当n≤16时,y=50n﹣50(17﹣n)=100n﹣850.
得
(2)解:设当天的利润不低于750元为事件A,由(2)得“利润不低于750元”等价于“需求量不低于16个”,则P(A)=0.7
27.【答案】
解:因为倾斜角α的范围是:0≤α<π,又由题意:sinα=,
所以:tanα=±,
直线过点P(0,2),由直线的点斜式方程得到:y﹣2=±x.
即:4x﹣3y+6=0或4x+3y﹣6=0.
28.【答案】
(1)解:二次函数
的对称轴为
,
的图象是抛物线,开口向上,对称轴为
;
当
时,
在
上是增函数;
,
;
当
时,
在
上是先减后增的函数,
当
时,
,当
时,
,
当
时,
在
上是减函数;
,
;
所以,
在
上的最小值是:
.
在
上的最大值是:
.
(2)解:由于此函数在区间
上是单调函数,
可得
的对称轴落在区间
外,
即
或
,解得
或
,
故
的取值范围是
或
;
29.【答案】
(1)解:根据题意,对任意的a,b∈R,满足f(a+b)=f(a)?f(b);
令a=1,b=0,则f(1)=f(0)?f(1),又由f(1)>1,则f(0)=1;
令a=1,b=﹣1,则f(0)=f(1)?f(﹣1),又由f(1)=2,则f(-1)=
(2)解:f(x)在(﹣∞,+∞)上单调递增;
任取x1
,
x2∈(﹣∞,+∞)且x1<x2
,
则有x2﹣x1>0,则f(x2﹣x1)>1,
f(x2)=f[(x2﹣x1)+x1]=f(x2﹣x1)?f(x1)>f(x1),
则f(x2)﹣f(x1)>0,
即函数f(x)为增函数
(3)解:根据题意,f(2)=f(1+1)=f(1)?f(1)=4,
则f(x+1)<4?f(x+1)<f(2)?x+1<2,
解可得:x<1,
即不等式的解集为(﹣∞,1).
30.【答案】
(1)解:因为
,
所以
对定义域
且
内的所有
都成立;
(2)解:因为
在
上单调递增,
所以当
时,
取得最小值,最小值为
,
当
时,
取得最大值,最大值为
,
所以
的值域为
.
(3)解:
,
当
,且
时,
,
若
,即
时,函数
在
和
上为增函数,所以
,
若
,即
且
时,
,
若
时,
的最小值不存在,
当
时,
,
若
,即
时,
,
若
,即
时,
在
上为减函数,
的最小值不存在,
又因为
时,
,
综上所述:当
且
时,
,
当
时,
的最小值不存在,
当
时,
,
当
时,
.
一、单选题
1.对任意的实数
,在下列命题中的真命题是(
??)
A.?“
”是“
”的必要不充分条件?????B.?“
”是“
”的必要不充分条件
C.?“
”是“
”的充分不必要条件?????D.?“
”是“
”的充分不必要条件
2.口袋内装有一些大小相同的红球、白球和黒球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0.28,那么摸出黒球的概率是( )
A.?0.42??????????????????????????????????????B.?0.28??????????????????????????????????????C.?0.3???????????????????????????????????????D.?0.7
3.已知
是等差数列,且
,则
的值是(???
)
A.??
24????????????????????????????????????????B.?27????????????????????????????????????????C.?30????????????????????????????????????????D.?33
4.如图,网格纸上小正方形变长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体体积为(??
)
A.??????????????????????????????????????B.???
B.?????????????????????????????????????C.?8?????????????????????????????????????D.?
5.已知偶函数f(x)在(0,+∞)上单调递增,则f(﹣3),f(﹣1),f(2)的大小关系是(?
)
A.?f(2)>f(﹣3)>f(﹣1)??????????????????????????????B.?f(﹣1)>f(2)>f(﹣3)
C.?f(﹣3)>f(﹣1)>f(2)??????????????????????????????D.?f(﹣3)>f(2)>f(﹣1)
6.已知函数,
则下列等式对恒成立的是(???)
A.f(-x)=f(x)
B.
C.
D.f(-x)=-sinx
7.设m,n表示不同的直线,α,β表示不同的平面,且m,n?α.则“α∥β”是“m∥β且n∥β”的( )
A.?充分但不必要条件???????????B.?必要但不充分条件???????????C.?充要条件???????????D.?既不充分又不必要条件
8.已知A=
,则a=(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?0???????????????????????????????????????????D.?
9.下列函数中,既是偶函数,又在区间(0,3)内是减函数的是(??
)
A.?y=2x﹣2﹣x??????????????????????????B.?y=cosx??????????????????????????C.?y=log2|x|??????????????????????????D.?y=x+x﹣1
10.在区间(0,3]上随机取一个数x,则事件“0≤log2x≤1”发生的概率为(??
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
11.已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.则该几何体的体积为(???
)
A.?48????????????????????????????????????????B.?64????????????????????????????????????????C.?96????????????????????????????????????????D.?192
12.已知函数
则函数y=f[f(x)]+1的零点个数是(?
)
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????C.?2???????????????????????????????????????????D.?1
13.已知函数
+2,则关于x的不等式f(3x+1)+f(x)>4的解集为(??
)
A.?(﹣
,+∞)???????????B.?(﹣
,+∞)???????????C.?(﹣
,+∞)???????????D.?(﹣
,+∞)
14.已知实数a1
,
a2
,
b1
,
b2
,
b3满足数列1,a1
,
a2
,
9是等差数列,数列1,b1
,
b2
,
b3
,
9是等比数列,则
的值为(??
)
A.?±
?????????????????????????????????????B.??????????????????????????????????????C.?﹣
?????????????????????????????????????D.?1
15.已知f(x)=,
则f()的值是( )
A.?0??????????????????????????????????????????B.?1??????????????????????????????????????????C.???????????????????????????????????????????D.?-
16.直线3x﹣4y﹣9=0被圆(x﹣3)2+y2=9截得的弦长为(??
)
A.?3???????????????????????????????????????????B.?4???????????????????????????????????????????C.?5???????????????????????????????????????????D.?6
17.下列四类函数中,具有性质“对任意的x>0,y>0,函数f(x)满足“f(x+y)=f(x)?f(y)”的是(??
)
A.?幂函数?????????????????????????????B.?对数函数?????????????????????????????
C.?指数函数?????????????????????????????D.?一次函数
18.在函数y=tanx、y=|sinx|、y=cos(2x+
)中,最小正周期为π的函数的个数为(??
)
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
19.若变量x,y满足约束条件
,则2x+y的最大值是(??
)
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
20.已知函数
(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象大致是(????
)
A.?????????????????B.?.????????????????
C.?????????????????D.?
二、填空题
21.函数y=
的定义域是________.
22.函数
的定义域为{0,1},则值域为________.
23.如图在四面体ABCD中,若截面PQMN是正方形,则在下列命题中正确的有________?.(填上有正确命题的序号)
①AC⊥BD
②AC=BD
③AC∥截面PQMN
④异面直线PM与BD所成的角为45°.
24.已知向量=(1,2),=(x,﹣4),若∥,
则?等于________?
25.对于正项数列
,定义
为
的“光阴”值,现知某数列的“光阴”值为
,则数列
的通项公式为________.
三、解答题
26.某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图3所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.若蛋糕店一天制作17个生日蛋糕.
(1)求当天的利润y(单位:元)关于当天需求量n(单位:个,n∈N)的函数解析式;
(2)求当天的利润不低于750元的概率.
27.设直线与y轴相交于点P(0,2),且它的倾斜角的正弦值是,
求该直线的方程
28.已知函数
(1)用
表示函数在
上的最值;
(2)求实数
的取值范围,使
在
上是单调函数.
29.定义在R上的函数y=f(x).对任意的a,b∈R.满足:f(a+b)=f(a)?f(b),当x>0时,有f(x)>1,其中f(1)=2.
(1)求f(0),f(﹣1)的值;
(2)判断该函数的单调性,并证明;
(3)求不等式f(x+1)<4的解集.
30.已知函数:
且
.
(1)证明:
对定义域内的所有
都成立;
(2)当
的定义域为
时,求证:
的值域为
;
(3)设函数
,求
的最小值.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
C
3.【答案】
D
4.【答案】A
5.【答案】
D
6.【答案】
C
7.【答案】
A
8.【答案】
B
9.【答案】B
10.【答案】
C
11.【答案】
B
12.【答案】
A
13.【答案】
D
14.【答案】B
15.【答案】
C
16.【答案】
D
17.【答案】
C
18.【答案】D
19.【答案】
C
20.【答案】
D
二、填空题
21.【答案】[4,+∞)
22.【答案】{0,
}
23.【答案】
①③④
24.【答案】
-10
25.【答案】
三、解答题
26.【答案】
(1)解:当n≥17时,y=17×(100﹣50)=850;
当n≤16时,y=50n﹣50(17﹣n)=100n﹣850.
得
(2)解:设当天的利润不低于750元为事件A,由(2)得“利润不低于750元”等价于“需求量不低于16个”,则P(A)=0.7
27.【答案】
解:因为倾斜角α的范围是:0≤α<π,又由题意:sinα=,
所以:tanα=±,
直线过点P(0,2),由直线的点斜式方程得到:y﹣2=±x.
即:4x﹣3y+6=0或4x+3y﹣6=0.
28.【答案】
(1)解:二次函数
的对称轴为
,
的图象是抛物线,开口向上,对称轴为
;
当
时,
在
上是增函数;
,
;
当
时,
在
上是先减后增的函数,
当
时,
,当
时,
,
当
时,
在
上是减函数;
,
;
所以,
在
上的最小值是:
.
在
上的最大值是:
.
(2)解:由于此函数在区间
上是单调函数,
可得
的对称轴落在区间
外,
即
或
,解得
或
,
故
的取值范围是
或
;
29.【答案】
(1)解:根据题意,对任意的a,b∈R,满足f(a+b)=f(a)?f(b);
令a=1,b=0,则f(1)=f(0)?f(1),又由f(1)>1,则f(0)=1;
令a=1,b=﹣1,则f(0)=f(1)?f(﹣1),又由f(1)=2,则f(-1)=
(2)解:f(x)在(﹣∞,+∞)上单调递增;
任取x1
,
x2∈(﹣∞,+∞)且x1<x2
,
则有x2﹣x1>0,则f(x2﹣x1)>1,
f(x2)=f[(x2﹣x1)+x1]=f(x2﹣x1)?f(x1)>f(x1),
则f(x2)﹣f(x1)>0,
即函数f(x)为增函数
(3)解:根据题意,f(2)=f(1+1)=f(1)?f(1)=4,
则f(x+1)<4?f(x+1)<f(2)?x+1<2,
解可得:x<1,
即不等式的解集为(﹣∞,1).
30.【答案】
(1)解:因为
,
所以
对定义域
且
内的所有
都成立;
(2)解:因为
在
上单调递增,
所以当
时,
取得最小值,最小值为
,
当
时,
取得最大值,最大值为
,
所以
的值域为
.
(3)解:
,
当
,且
时,
,
若
,即
时,函数
在
和
上为增函数,所以
,
若
,即
且
时,
,
若
时,
的最小值不存在,
当
时,
,
若
,即
时,
,
若
,即
时,
在
上为减函数,
的最小值不存在,
又因为
时,
,
综上所述:当
且
时,
,
当
时,
的最小值不存在,
当
时,
,
当
时,
.
同课章节目录
