上海市浦东新区2020-2021学年度八年级上期期末数学试(word版含答案)
文档属性
| 名称 | 上海市浦东新区2020-2021学年度八年级上期期末数学试(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 760.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 00:00:00 | ||
图片预览




文档简介
上海市浦东新区第四教育署八年级上学期期末数学试题
一、选择题:本大题共6个小题,每小题2分,共12分.
1.
下列计算结果正确的是(
)
A.
B.
C.
D.
2.
一元二次方程根的情况是(
)
A.
有两个相等的实数根;
B.
有两个不相等的实数根;
C.
没有实数根;
D.
无法确定.
3.
在△ABC中,BC=6,AC=8,AB=10,则该三角形为( )
A
锐角三角形
B.
直角三角形
C.
纯角三角形
D.
等腰直角三角形
4.
若点在反比例函数的图象上,且,则下列各式正确的是(
)
A.
B.
C.
D.
5.
对于下列说法:
①角平分线上任意一点到角两边的距离相等;
②等腰三角形的高、中线、角平分线互相重合;
③三角形三边中垂线交点到三个顶点的距离相等;
④直角三角形只有一条高线.
正确的有(
)
A.
①②③④
B.
①③
C.
①②③
D.
①②④
6.
如图,在中,点在边上,垂直平分边,垂足为点,若且,则的度数是(
)
A.
B.
C.
D.
二、填空题(本大题共有12小题,每题3分,满分36分)
7.
计算:=________.
8.
方程的根是
_______________.
9.
在实数范围内分解因式:=____________.
10.
函数的定义域是______________.
11.
已知函数,那么=_________.
12.
平面直角坐标系中,点P(-4,2)到坐标原点的距离是____________
13.
电影《中国机长》首映当日票房已经达到1.92亿元,2天后当日票房达到2.61亿元,设平均每天票房的增长率为x,则可列方程为___.
14.
如果正比例函数的图像经过第一、三象限,那么的取值范围是
__.
15.
如图,△ABC中,AB=8,BC=10,BD是△ABC的角平分线,DE⊥AB于点E,若DE=4,则三角形ABC的面积为______.
16.
如图,中,平分,的中垂线交于点,交于点,连接.若,,则的度数为=______.
17.
如图,中,,,,,平分,与相交于点,则长等于_____.
18.
如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=和y=
在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交y=的图象于点C,连接AC.若△ABC是等腰三角形,则k的值是_____.
三、解答题:本大题共8小题,共52分)
19.
计算:
20.
解方程:
21.
已知,其中与成正比例,与成反比例,并且当时,;当时,,求关于的函数解析式.
22.
如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.
23.
直角坐标平面内,已知点,,在轴上求一点,使得是以为直角的直角三角形.
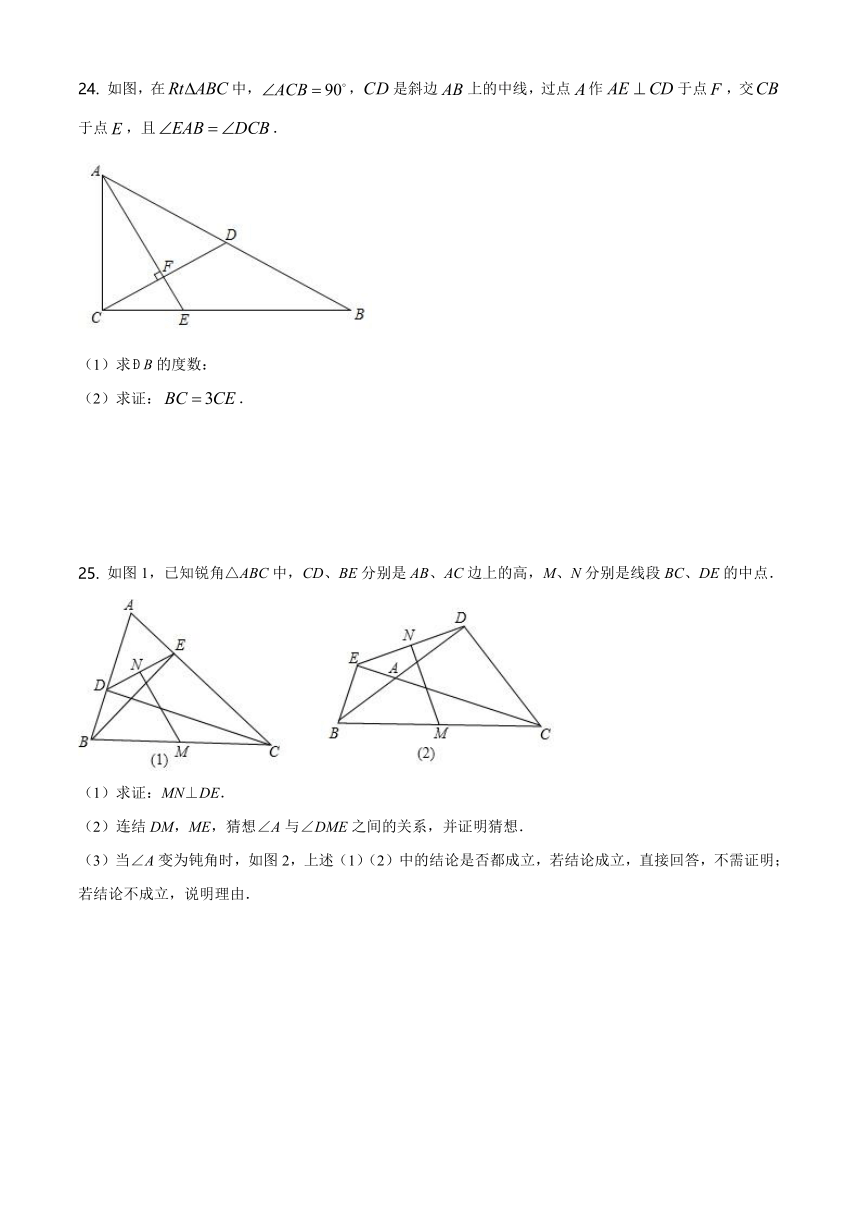
24.
如图,在中,,是斜边上的中线,过点作于点,交于点,且.
(1)求的度数:
(2)求证:.
25.
如图1,已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE.
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想.
(3)当∠A变为钝角时,如图2,上述(1)(2)中的结论是否都成立,若结论成立,直接回答,不需证明;若结论不成立,说明理由.
26.
阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)理解并填空:
①根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
(填“是”或“不是”)
②若某三角形的三边长分别为1、、2,则该三角形
(填“是”或“不是”)奇异三角形.
(2)探究:在中,两边长分别,且,,则这个三角形是否是奇异三角形?请说明理由.
参考答案
1-6.BCBCBD
7.
8.
,
9.
10.
且
11.
2.
12.
13.
1.92(1+x)2=2.61.
14.
k>3
15.36
16.
17.
3
∴DE=DH-EH=5=2=3.
18.
19.
解:
=
=.
20.
解:其中,
得
即或
所以原方程的根是
21.
解:∵y1与x2成正比例,y2与x成反比例,
∴y1=kx2,y2=,
∵y=y1+y2,
∴y=kx2+,
∵当x=时y=5,当x=1时y=-1,
∴,
解得:,
∴y与x之间的函数关系式为y=-4x2+.
22.
解:连接BD.如图所示:
∵∠C=90°,BC=15米,CD=20米,
∴BD===25(米);
在△ABD中,∵BD=25米,AB=24米,DA=7米,
242+72=252,即AB2+BD2=AD2,
∴△ABD是直角三角形.
∴S四边形ABCD=S△ABD+S△BCD
=AB?AD+BC?CD
=×24×7+×15×20
=84+150
=234(平方米);
即绿地ABCD的面积为234平方米.
23.
解:设
由勾股定理得:,
,
,
∵,
∴,
即,
解得:,,
∴点的坐标为或.
24.
解(1)∵,
∴,
∴,
∴,
∵,
∴,
∵是斜边上的中线,,
∴,
∴,
∴,
∵,
∴,
(2)∵,
∴,,
∴,
25.
解:(1)证明:如图,连接,,
、分别是、边上的高,是的中点,
,,
,
又为中点,
;
(2)在中,,
,
∴,,
,
,
,
,
;
(3)结论(1)成立,结论(2)不成立,
理由如下:如图,
同理(1)可知:,故结论(1)正确;
,
∴,,
在中,,
,
,故结论(2)不正确.
26.
解:(1)①设等边三角形的边长为a,则,
∴等边三角形一定是奇异三角形,
故答案为:是;
②∵,2×=8,
∴
∴该三角形是奇异三角形,
故答案为:是;
(2)当c为斜边时,则,
则
∴Rt△ABC不是奇异三角形;
当b为斜边时,,
则有,
∴Rt△ABC是奇异三角形,
答:当为斜边时,不是奇异三角形;当为斜边时,是奇异三角形.
一、选择题:本大题共6个小题,每小题2分,共12分.
1.
下列计算结果正确的是(
)
A.
B.
C.
D.
2.
一元二次方程根的情况是(
)
A.
有两个相等的实数根;
B.
有两个不相等的实数根;
C.
没有实数根;
D.
无法确定.
3.
在△ABC中,BC=6,AC=8,AB=10,则该三角形为( )
A
锐角三角形
B.
直角三角形
C.
纯角三角形
D.
等腰直角三角形
4.
若点在反比例函数的图象上,且,则下列各式正确的是(
)
A.
B.
C.
D.
5.
对于下列说法:
①角平分线上任意一点到角两边的距离相等;
②等腰三角形的高、中线、角平分线互相重合;
③三角形三边中垂线交点到三个顶点的距离相等;
④直角三角形只有一条高线.
正确的有(
)
A.
①②③④
B.
①③
C.
①②③
D.
①②④
6.
如图,在中,点在边上,垂直平分边,垂足为点,若且,则的度数是(
)
A.
B.
C.
D.
二、填空题(本大题共有12小题,每题3分,满分36分)
7.
计算:=________.
8.
方程的根是
_______________.
9.
在实数范围内分解因式:=____________.
10.
函数的定义域是______________.
11.
已知函数,那么=_________.
12.
平面直角坐标系中,点P(-4,2)到坐标原点的距离是____________
13.
电影《中国机长》首映当日票房已经达到1.92亿元,2天后当日票房达到2.61亿元,设平均每天票房的增长率为x,则可列方程为___.
14.
如果正比例函数的图像经过第一、三象限,那么的取值范围是
__.
15.
如图,△ABC中,AB=8,BC=10,BD是△ABC的角平分线,DE⊥AB于点E,若DE=4,则三角形ABC的面积为______.
16.
如图,中,平分,的中垂线交于点,交于点,连接.若,,则的度数为=______.
17.
如图,中,,,,,平分,与相交于点,则长等于_____.
18.
如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=和y=
在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交y=的图象于点C,连接AC.若△ABC是等腰三角形,则k的值是_____.
三、解答题:本大题共8小题,共52分)
19.
计算:
20.
解方程:
21.
已知,其中与成正比例,与成反比例,并且当时,;当时,,求关于的函数解析式.
22.
如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.
23.
直角坐标平面内,已知点,,在轴上求一点,使得是以为直角的直角三角形.
24.
如图,在中,,是斜边上的中线,过点作于点,交于点,且.
(1)求的度数:
(2)求证:.
25.
如图1,已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE.
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想.
(3)当∠A变为钝角时,如图2,上述(1)(2)中的结论是否都成立,若结论成立,直接回答,不需证明;若结论不成立,说明理由.
26.
阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)理解并填空:
①根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
(填“是”或“不是”)
②若某三角形的三边长分别为1、、2,则该三角形
(填“是”或“不是”)奇异三角形.
(2)探究:在中,两边长分别,且,,则这个三角形是否是奇异三角形?请说明理由.
参考答案
1-6.BCBCBD
7.
8.
,
9.
10.
且
11.
2.
12.
13.
1.92(1+x)2=2.61.
14.
k>3
15.36
16.
17.
3
∴DE=DH-EH=5=2=3.
18.
19.
解:
=
=.
20.
解:其中,
得
即或
所以原方程的根是
21.
解:∵y1与x2成正比例,y2与x成反比例,
∴y1=kx2,y2=,
∵y=y1+y2,
∴y=kx2+,
∵当x=时y=5,当x=1时y=-1,
∴,
解得:,
∴y与x之间的函数关系式为y=-4x2+.
22.
解:连接BD.如图所示:
∵∠C=90°,BC=15米,CD=20米,
∴BD===25(米);
在△ABD中,∵BD=25米,AB=24米,DA=7米,
242+72=252,即AB2+BD2=AD2,
∴△ABD是直角三角形.
∴S四边形ABCD=S△ABD+S△BCD
=AB?AD+BC?CD
=×24×7+×15×20
=84+150
=234(平方米);
即绿地ABCD的面积为234平方米.
23.
解:设
由勾股定理得:,
,
,
∵,
∴,
即,
解得:,,
∴点的坐标为或.
24.
解(1)∵,
∴,
∴,
∴,
∵,
∴,
∵是斜边上的中线,,
∴,
∴,
∴,
∵,
∴,
(2)∵,
∴,,
∴,
25.
解:(1)证明:如图,连接,,
、分别是、边上的高,是的中点,
,,
,
又为中点,
;
(2)在中,,
,
∴,,
,
,
,
,
;
(3)结论(1)成立,结论(2)不成立,
理由如下:如图,
同理(1)可知:,故结论(1)正确;
,
∴,,
在中,,
,
,故结论(2)不正确.
26.
解:(1)①设等边三角形的边长为a,则,
∴等边三角形一定是奇异三角形,
故答案为:是;
②∵,2×=8,
∴
∴该三角形是奇异三角形,
故答案为:是;
(2)当c为斜边时,则,
则
∴Rt△ABC不是奇异三角形;
当b为斜边时,,
则有,
∴Rt△ABC是奇异三角形,
答:当为斜边时,不是奇异三角形;当为斜边时,是奇异三角形.
同课章节目录
