第七章生活中的轴对称

(共37张PPT)
第七章
生活中的轴对称
自远古以来，对称的形式被认为是和谐、美丽并且真实的．不论在自然界里还是在建筑中，不论在艺术中还是在科学中，甚至最普通的日常生活用品中，对称的形式都随处可见．
山倒映在湖中，建筑物倒映水中……这些都是令人难忘的对称景象．
请你想一想：将上图中的每一个图形沿某条直线对折，直线两旁的部分能完全重合吗？
如果一个图形沿某条直线对折，对折的两部分是完全重合的，那么就称这样的图形称为轴对称图形 （a figure of line symmetry）.
这条直线叫做这个图形的对称轴（axis of symmetry）．
试一试
一定要熟记！
认一认
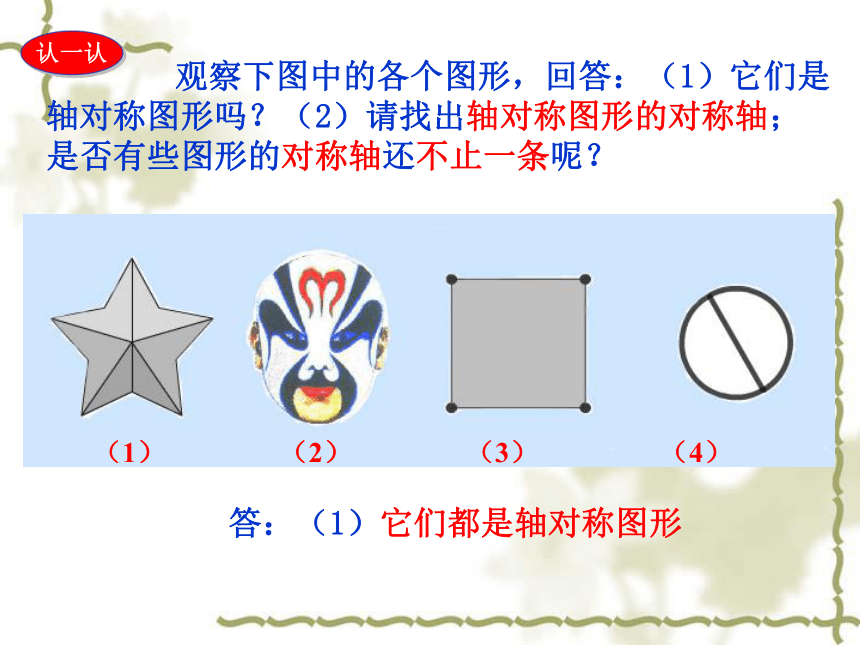
观察下图中的各个图形，回答：（1）它们是轴对称图形吗？（2）请找出轴对称图形的对称轴；是否有些图形的对称轴还不止一条呢？
（1） （2） （3） （4）
答：（1）它们都是轴对称图形
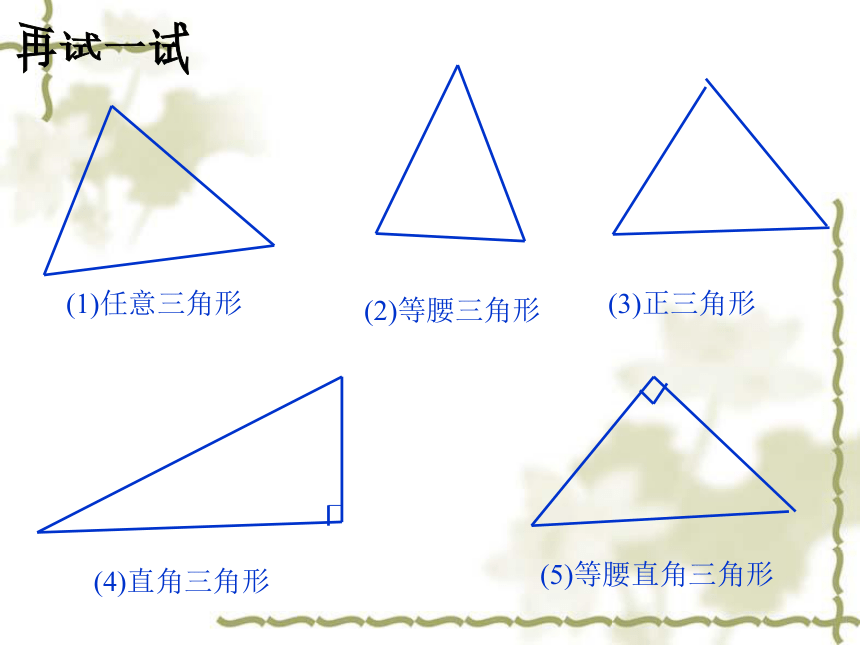
(1)任意三角形
(2)等腰三角形
(3)正三角形
(4)直角三角形
(5)等腰直角三角形
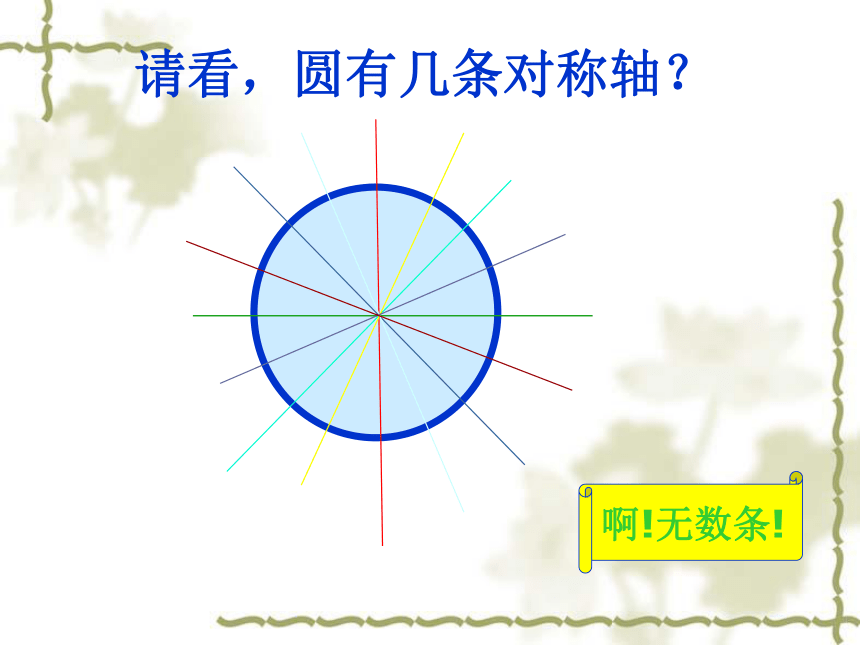
请看，圆有几条对称轴？
啊!无数条!
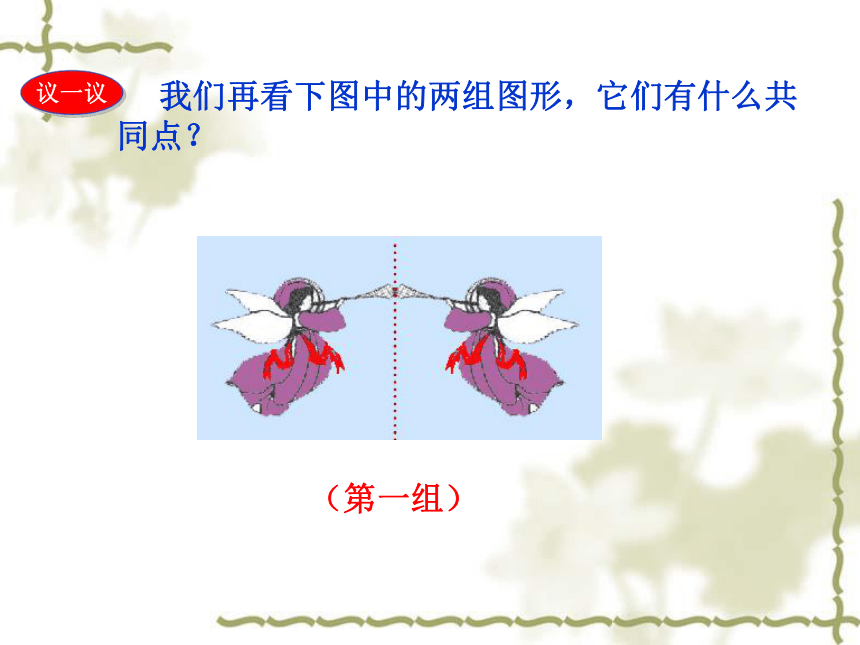
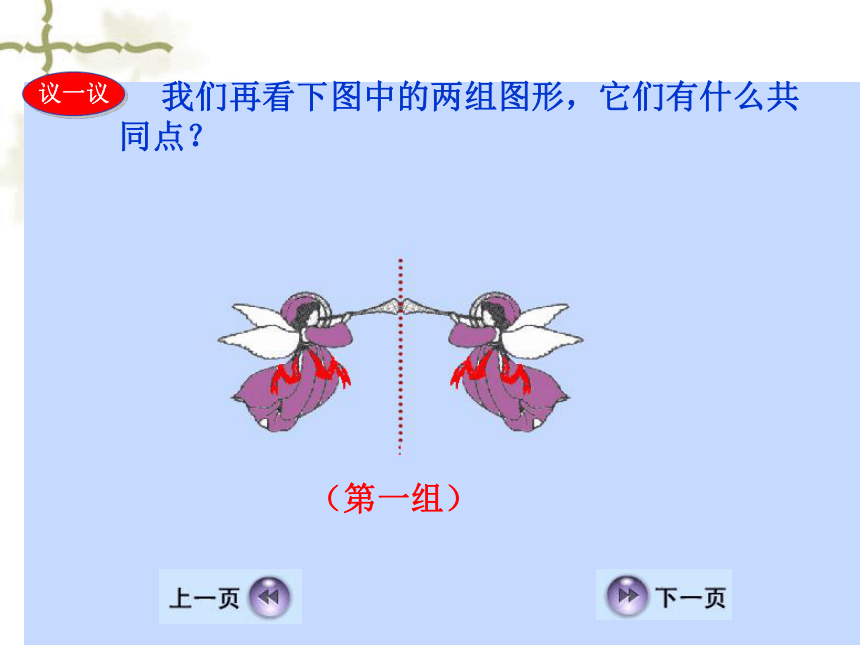
我们再看下图中的两组图形，它们有什么共同点？
议一议
（第一组）
议一议
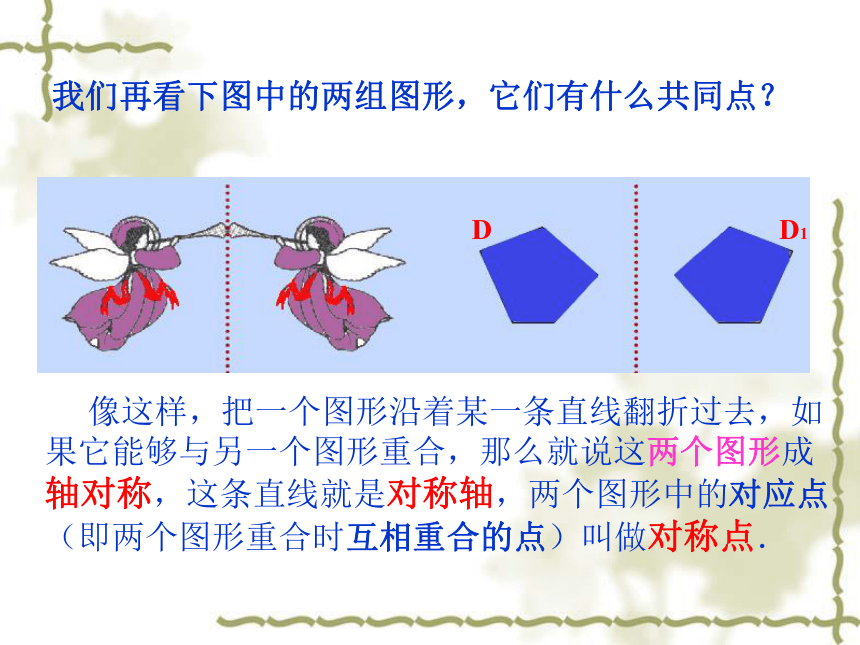
我们再看下图中的两组图形，它们有什么共同点？
（第一组）
我们再看下图中的两组图形，它们有什么共同点？
像这样，把一个图形沿着某一条直线翻折过去，如果它能够与另一个图形重合，那么就说这两个图形成轴对称，这条直线就是对称轴，两个图形中的对应点（即两个图形重合时互相重合的点）叫做对称点．
D D1
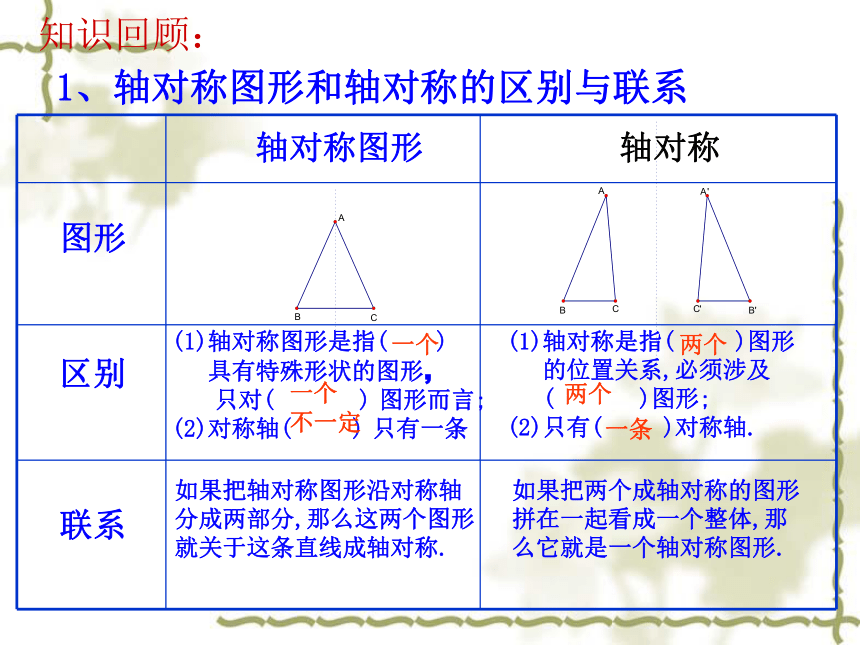
1、轴对称图形和轴对称的区别与联系
轴对称图形
轴对称
区别
联系
图形
(1)轴对称图形是指( )
具有特殊形状的图形,
只对( ) 图形而言;
(2)对称轴( ) 只有一条
(1)轴对称是指( )图形
的位置关系,必须涉及
( )图形;
(2)只有( )对称轴.
如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称.
如果把两个成轴对称的图形
拼在一起看成一个整体,那
么它就是一个轴对称图形.
一个
一个
不一定
两个
两个
一条
知识回顾：
1.等腰三角形的性质
①.等腰三角形的两个底角相等。（等边对等角）
②.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。（三线合一）
2、等腰三角形的判定：
如果一个三角形有两个角相等，那么这两个角所对的边也相等。（等角对等边）
1.等边三角形的性质：
等边三角形的三个角都相等，并且每一个角都等于600 。
2、等边三角形的判定：
①三个角都相等的三角形是等边三角形。
②有一个角是600的等腰三角形是等边三角形。
3.在直角三角形中，如果一个锐角等于300，那么它所对的直角边等于斜边的一半。
1、什么是“轴对称”和“对称轴”
如果一个图形沿一条直线折叠, 直线两侧的图形能够互相重合, 这个图形就叫做轴对称图形, 这条直线叫做这个图形的对称轴。
2.轴对称图形的基本性质是什么
对应点的连线被对称轴__________;对应线段_________;对应角_______.
垂直平分
相等
相等
3.角是轴对称图形，_________是它的对称轴，角平分线上的点到角的两边距离________.
线段也是轴对称图形,____________
是它的对称轴,线段垂直平分线上的点到线段的两个端点距离________.
角平分线
线段垂直平分线
相等
相等
4、小明照镜子的时候，发现T恤上的英文单词在镜子中呈现“ ”的样子，请你判断这个英文单词是（ ）
(A)
(B)
(C)
(D)
A
加拿大 韩国 澳大利亚 乌拉圭 瑞典 瑞士
C
5. 国旗是一个国家的象征，观察下面的国旗，是轴对称图形的是 （ ）
A.加拿大、韩国、乌拉圭
B.加拿大、瑞典、澳大利亚
C.加拿大、瑞典、瑞士
D.乌拉圭、瑞典、瑞士
6. ① 如图, AB//CD,∠ACD的角平分线交AB于E,想一想△ACE是什么三角形.
7. ②如图, ∠ABC、∠ACB的平分线相交于F, 过F作DE//BC交AB于D, 交AC于E,若AB=9cm, AC=8cm, 则△ADE的周长是多少
F
E
D
C
B
A
AC=AE+EC=AE+EF
AB=AD+DB=AD+DF
1.如图: 点B、C、D、E、F在∠MAN的边上, ∠A=15o, AB=BC=CD＝DE=EF，求∠ MEF的度数。
A
B
C
D
E
F
M
N
答: ∠ MEF的度数=75 °
——数学就在你身边
2、社区服务部为了方便居民取奶，要在街道上修建一个奶站，给住宅A区和B区的居民供奶
A区
B区
街道
M
（1）奶站建在街道的什么位置才能使它到A区和B区的距离之和最短？
A区
B区
街道
怎么建呢？为什么？
C
O
（2）如果想使这个奶站到A区和B区的距离相等，应将它建在街道的什么位置呢？
A区
B区
街道
C
(3) 如果是奶站工人送奶，你认为哪种建法比较合理？如果是居民自己取奶，你认为哪种建法合理呢？请联系实际说明理由。
1.轴对称图形的对称轴的条数( )
A. 只有1条 B. 2条
C. 3条 D. 至少一条
2.下列图形中对称轴最多的是( )
A. 圆 B. 正方形
C. 角 D. 线段?
D
A
3.下面几何图形中,其中一定是轴对称图形的有 ( )个
⑴线段 ⑵角 ⑶等腰三角形 ⑷直角三角形 ⑸等腰梯形 ⑹平行四边形
A.1 B.2 C.3 D.4?
4.小明从镜子里看到镜子对面的钟表里的时间是2点30分，实际时间为　　　点______　　　分．
D
9
30
5.如图, △ABC的周长为19cm，AC的垂直平分线DE交BC于D，E为垂足，AE=3cm，则△ABD的周长为_____cm.
13
1. A、B、C三所居民区之间有一个三角形花坛，现决定在花坛中建一凉亭，使三个居民区到凉亭的距离相等，建在哪儿好？
A
B
C
倘若要使凉亭到AB、BC、AC这三条小路的距离相等，它应建在什么位置呢？
A
B
C
2.如图：C为马厩，D为帐篷，牧马人某一天要从马厩牵出马，先到草地边某一处牧马，再到河边饮马，然后回到帐篷，请你帮他确定这一天的最短路线，
作法：1.作点C关于直线
OA 的 对称点点F,
2. 作点D关于直线 OB
的对称点点E,
3.连接EF分别交直线OA.OB于点G.H，
则CG+GH+DH最短.
F
A
O
B
D ·
· C
E
G
H
证明：在直线OA 上另外任取一点G，连接…
∵点F,点C关于直线OA对称，点G.M在OA上，∴GF=GC,FM=CM,
同理HD=HE，ND=NE,
∴CM+MN+ND=FM+MN+NE=FE,
CG+GH+HD=FG+GH+HE,
在四边形EFGH中，
∵FG+GH+HE＞FE（两点之间，线段最短），
即CG+GH+HD＞CM+MN+ND 即CM+MN+ND最短.
F
A
O
B
D ·
· C
E
M
N
G
H
3.如图，A, B两地在一条河的两岸，现要在河上建一座桥MN，桥造在何处才能使从A到B的路径AMNB最短？（假设河的两岸是平行的直线，桥要与河垂直）
A·
B
3.如图，A, B两地在一条河的两岸，现要在河上建一座桥MN，桥造在何处才能使从A到B的路径AMNB最短？（假设河的两岸是平行的直线，桥要与河垂直）
A·
B
M
N
E
作法：1.将点B沿垂直与河岸的方向平移一个河宽到E，
2.连接AE交河对岸与点M,
则点M为建桥的位置，MN为所建的桥。
证明：由平移的性质，得 BN∥EM 且BN=EM, MN=CD, BD∥CE, BD=CE,
所以A.B两地的距:AM+MN+BN=AM+MN+EM=AE+MN,
若桥的位置建在CD处，连接AC.CD.DB.CE,
则AB两地的距离为：
AC+CD+DB=AC+CD+CE=AC+CE+MN,
在△ACE中，∵AC+CE＞AE,
∴AC+CE+MN＞AE+MN,
即AC+CD+DB ＞AM+MN+BN
所以桥的位置建在CD处，AB两地的路程最短。
A·
B
M
N
E
C
D
1.如果一个图形沿某条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形；这条直线叫做对称轴。
2.角平分线上的点到角两边距离相等。
3.线段垂直平分线上的任意一点到线段两个端点的距离相等。
4.角、线段和等腰三角形是轴对称图形。
5.等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合，简称为“三线合一”。
6.轴对称图形上对应点所连的线段被对称轴垂直平分。
7.轴对称图形上对应线段相等、对应角相等。