2021年高考数学真题模拟试题专项汇编之不等式、推理与证明、算法初步(Word版,含解析)
文档属性
| 名称 | 2021年高考数学真题模拟试题专项汇编之不等式、推理与证明、算法初步(Word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 766.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 10:06:49 | ||
图片预览

文档简介
(7)不等式、推理与证明、算法初步——2021年高考数学真题模拟试题专项汇编
1.【2021年全国乙卷(文),5】若x,y满足约束条件则的最小值为(
)
A.18
B.10
C.6
D.4
2.【2021年浙江卷,5】若实数x,y满足约束条件,则的最小值是(
)
A.-2
B.
C.
D.
3.【2021年安徽桐城模拟,4】设满足约束条件,则的最大值为(
)
A.
3
B.
C.
1
D.
4.【2021年山东泰安模拟,5】劳动教育是中国特色社会主义教育制度的重要内容,直接决定了社会主义建设者和接班人的劳动价值取向、劳动精神面貌和劳动技能水平.新学期到来,某大学开出了烹饪选修课,共18学时,面向2020级本科生和强基计划学生开放.该校学生小华选完内容后,其他三位同学根据小华的兴趣爱好对他选择的内容进行猜测.
甲说:“小华选的不是川菜干烧大虾,选的是烹制中式面食.”乙说:“小华选的不是烹制中式面食,选的是烹制西式点心.”丙说:“小华选的不是烹制中式面食,也不是青椒土豆丝.”已知三人中有一个人说的全对,有一个人说的对了一半,剩下的一个人说的全不对,由此推断小华选择的内容(
)
A.可能是青椒土豆丝
B.可能是川菜干烧大虾
C.可能是烹制西式点心
D.一定是烹制中式面食
5.【2021年广东珠海模拟,6】变量x,y满足约束条件,若目标函数的最大值为12,则实数(
)
A.12
B.-12
C.4
D.-4
6.【2021年全国乙卷(理),8】在区间与中各随机取1个数,则两数之和大于的概率为(
)
A.
B.
C.
D.
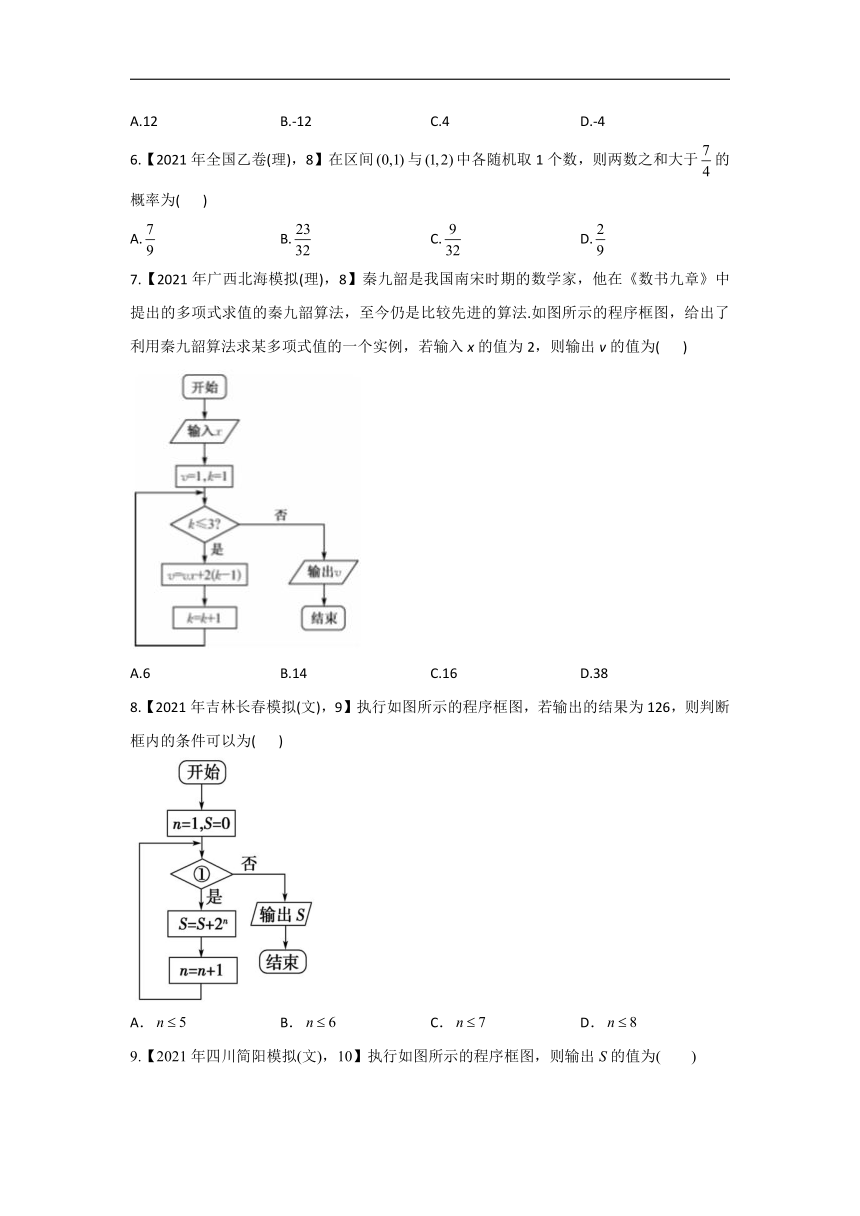
7.【2021年广西北海模拟(理),8】秦九韶是我国南宋时期的数学家,他在《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图,给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为(
)
A.6
B.14
C.16
D.38
8.【2021年吉林长春模拟(文),9】执行如图所示的程序框图,若输出的结果为126,则判断框内的条件可以为(
)
A.
B.
C.
D.
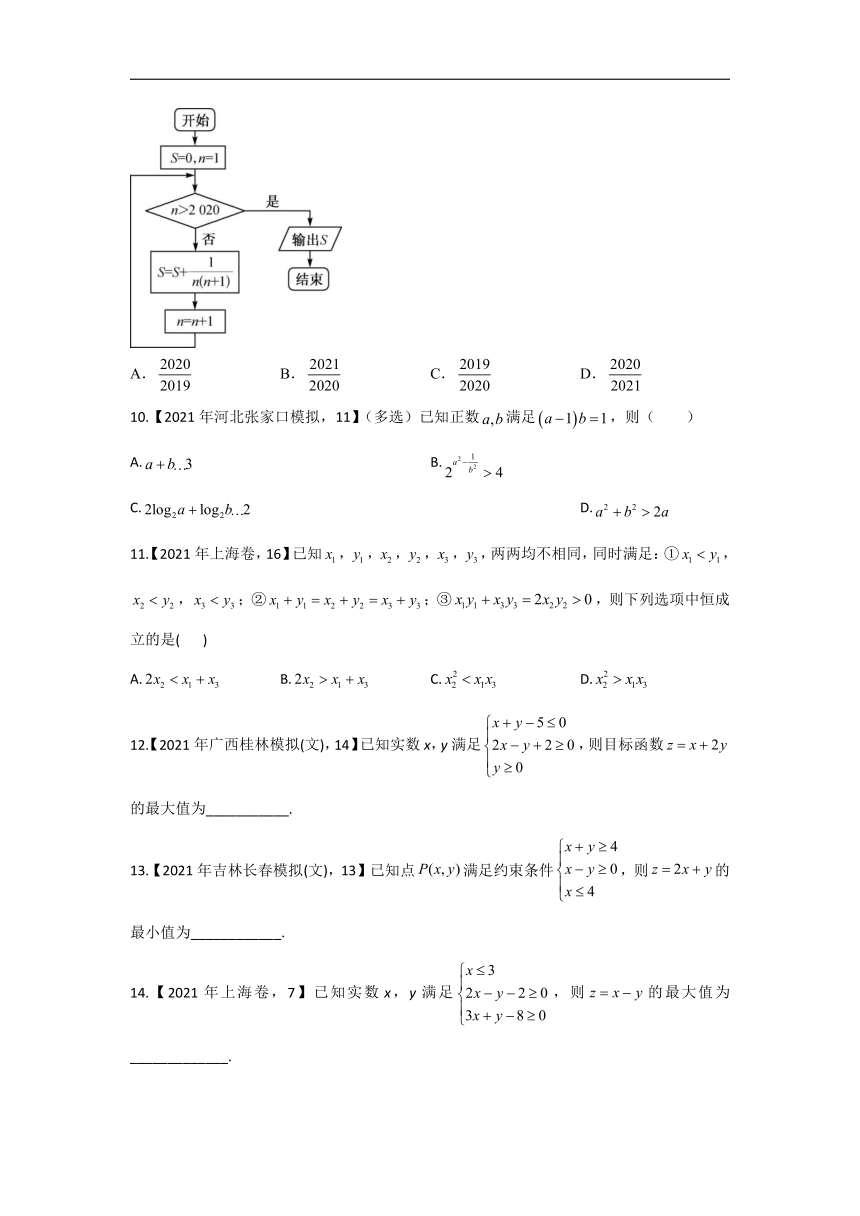
9.【2021年四川简阳模拟(文),10】执行如图所示的程序框图,则输出S的值为(
)
A.
B.
C.
D.
10.【2021年河北张家口模拟,11】(多选)已知正数满足,则(
)
A.
B.
C.
D.
11.【2021年上海卷,16】已知,,,,,,两两均不相同,同时满足:①,,;②;③,则下列选项中恒成立的是(
)
A.
B.
C.
D.
12.【2021年广西桂林模拟(文),14】已知实数x,y满足,则目标函数的最大值为___________.
13.【2021年吉林长春模拟(文),13】已知点满足约束条件,则的最小值为____________.
14.【2021年上海卷,7】已知实数x,y满足,则的最大值为_____________.
答案以及解析
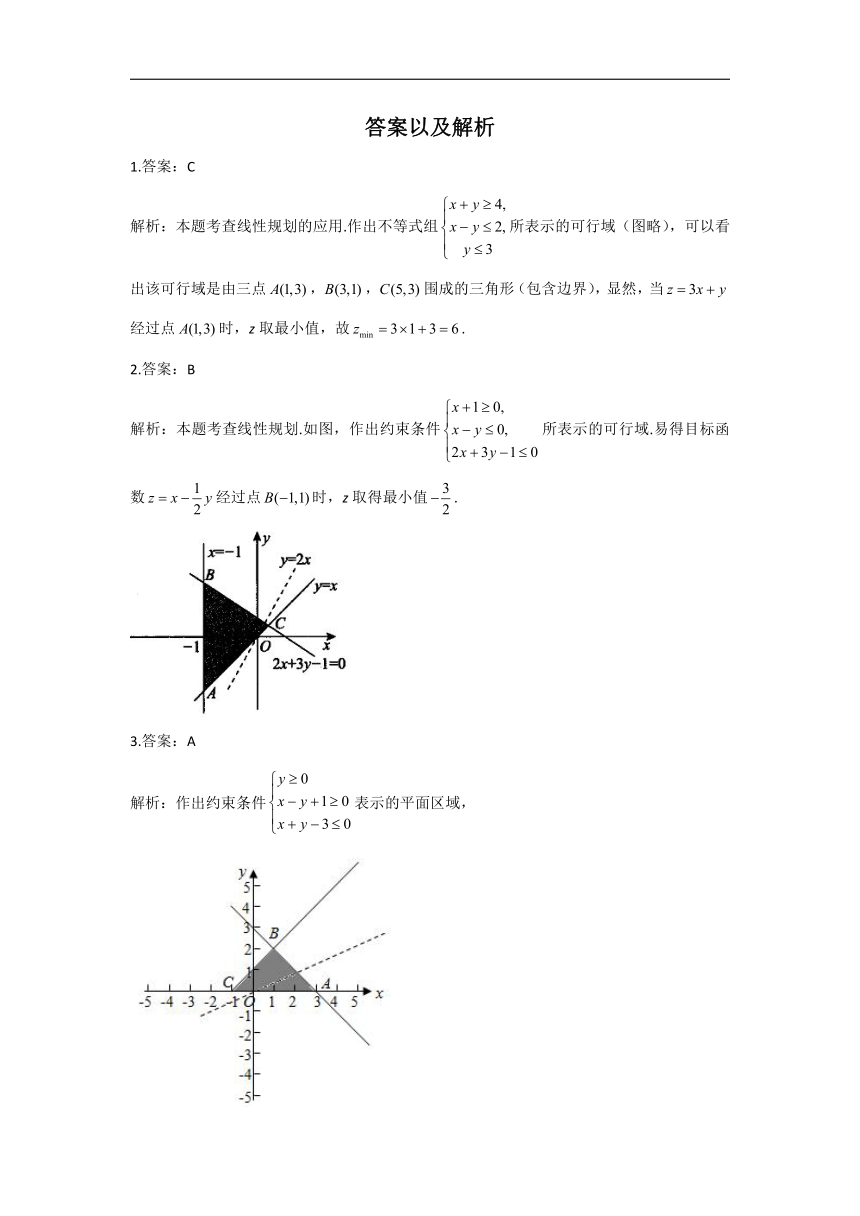
1.答案:C
解析:本题考查线性规划的应用.作出不等式组所表示的可行域(图略),可以看出该可行域是由三点,,围成的三角形(包含边界),显然,当经过点时,z取最小值,故.
2.答案:B
解析:本题考查线性规划.如图,作出约束条件所表示的可行域.易得目标函数经过点时,z取得最小值.
3.答案:A
解析:作出约束条件表示的平面区域,
得到如图的及其内部,其中,,
设,将直线进行平移,
当l经过点A时,目标函数z达到最大值.
故选:A.
4.答案:B
解析:若小华选择的青椒土豆丝,则甲、乙、丙都各对一半,排除;若小华选择的川菜干烧大虾,则甲全不对,乙对一半,丙全对,符合;若小华选择的制西式点心,则甲对一半,乙全对,丙全对,不符合,排除;若小华选择的烹制中式面食,则甲全对,乙全不对,丙对一半,符合;由此推断小华选择的内容可能是川菜干烧大虾或烹制中式面食.
所以选B.
5.答案:B
解析:解:根据约束条件得,如图当最优解是时,目标函数得到最大值得,故选B.
6.答案:B
解析:本题考查简单的线性规划及其应用、几何概型的概率问题.由题目条件设,,且,则作出对应的平面区域如图所示,可知所求的概率为.
7.答案:C
解析:程序运行过程如下:
,;,;,;,,跳出循环,输出v的值为16.故选C.
8.答案:B
解析:根据框图,执行程序,
;
;
……
,
令,
解得,即时结束程序,
所以,
故选:B.
9.答案:D
解析:第一次循环,不成立,,;
第二次循环,不成立,,;
以此类推,执行最后一次循环,不成立,,;成立,输出.
故选:D.
10.答案:ACD
解析:由,得,又,所以,故A正确;
因为,所以当时,,此时,故B错误;
,所以,故C正确;
又,所以,故D正确.
所以选
11.答案:A
解析:设,
由题可得,且,
由③得,
则有,
因为
所以,
故A选项正确;
上面已证,
因为不知道m的正负,
所以该式子的正负无法恒定.
故选A.
12.答案:9
解析:作出不等式组对应的平面区域如图:由,得表示斜率为,纵截距为的一组平行直线,平移直线,当直线经过点时,此时直线截距最大,z最大,此时.
13.答案:6
解析:由约束条件,画出可行域如图所示阴影部分:
将目标函数转化为,平移直线,
当直线经过点A时,直线在y轴上截距最小,此时,目标函数取得最小值,
由,解得,
所以,
所以目标函数的最小值为,
故答案为6.
14.答案:4
解析:本题主要考查线性规划.根据题中所给约束条件可作出可行域如图所示,目标函数可化为,当z最大时,直线在y轴上的截距最小,由图可知当直线过直线和直线的交点时,截距最小,联立,解得,此时,所以z最大值为4.故本题正确答案为4.
1.【2021年全国乙卷(文),5】若x,y满足约束条件则的最小值为(
)
A.18
B.10
C.6
D.4
2.【2021年浙江卷,5】若实数x,y满足约束条件,则的最小值是(
)
A.-2
B.
C.
D.
3.【2021年安徽桐城模拟,4】设满足约束条件,则的最大值为(
)
A.
3
B.
C.
1
D.
4.【2021年山东泰安模拟,5】劳动教育是中国特色社会主义教育制度的重要内容,直接决定了社会主义建设者和接班人的劳动价值取向、劳动精神面貌和劳动技能水平.新学期到来,某大学开出了烹饪选修课,共18学时,面向2020级本科生和强基计划学生开放.该校学生小华选完内容后,其他三位同学根据小华的兴趣爱好对他选择的内容进行猜测.
甲说:“小华选的不是川菜干烧大虾,选的是烹制中式面食.”乙说:“小华选的不是烹制中式面食,选的是烹制西式点心.”丙说:“小华选的不是烹制中式面食,也不是青椒土豆丝.”已知三人中有一个人说的全对,有一个人说的对了一半,剩下的一个人说的全不对,由此推断小华选择的内容(
)
A.可能是青椒土豆丝
B.可能是川菜干烧大虾
C.可能是烹制西式点心
D.一定是烹制中式面食
5.【2021年广东珠海模拟,6】变量x,y满足约束条件,若目标函数的最大值为12,则实数(
)
A.12
B.-12
C.4
D.-4
6.【2021年全国乙卷(理),8】在区间与中各随机取1个数,则两数之和大于的概率为(
)
A.
B.
C.
D.
7.【2021年广西北海模拟(理),8】秦九韶是我国南宋时期的数学家,他在《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图,给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为(
)
A.6
B.14
C.16
D.38
8.【2021年吉林长春模拟(文),9】执行如图所示的程序框图,若输出的结果为126,则判断框内的条件可以为(
)
A.
B.
C.
D.
9.【2021年四川简阳模拟(文),10】执行如图所示的程序框图,则输出S的值为(
)
A.
B.
C.
D.
10.【2021年河北张家口模拟,11】(多选)已知正数满足,则(
)
A.
B.
C.
D.
11.【2021年上海卷,16】已知,,,,,,两两均不相同,同时满足:①,,;②;③,则下列选项中恒成立的是(
)
A.
B.
C.
D.
12.【2021年广西桂林模拟(文),14】已知实数x,y满足,则目标函数的最大值为___________.
13.【2021年吉林长春模拟(文),13】已知点满足约束条件,则的最小值为____________.
14.【2021年上海卷,7】已知实数x,y满足,则的最大值为_____________.
答案以及解析
1.答案:C
解析:本题考查线性规划的应用.作出不等式组所表示的可行域(图略),可以看出该可行域是由三点,,围成的三角形(包含边界),显然,当经过点时,z取最小值,故.
2.答案:B
解析:本题考查线性规划.如图,作出约束条件所表示的可行域.易得目标函数经过点时,z取得最小值.
3.答案:A
解析:作出约束条件表示的平面区域,
得到如图的及其内部,其中,,
设,将直线进行平移,
当l经过点A时,目标函数z达到最大值.
故选:A.
4.答案:B
解析:若小华选择的青椒土豆丝,则甲、乙、丙都各对一半,排除;若小华选择的川菜干烧大虾,则甲全不对,乙对一半,丙全对,符合;若小华选择的制西式点心,则甲对一半,乙全对,丙全对,不符合,排除;若小华选择的烹制中式面食,则甲全对,乙全不对,丙对一半,符合;由此推断小华选择的内容可能是川菜干烧大虾或烹制中式面食.
所以选B.
5.答案:B
解析:解:根据约束条件得,如图当最优解是时,目标函数得到最大值得,故选B.
6.答案:B
解析:本题考查简单的线性规划及其应用、几何概型的概率问题.由题目条件设,,且,则作出对应的平面区域如图所示,可知所求的概率为.
7.答案:C
解析:程序运行过程如下:
,;,;,;,,跳出循环,输出v的值为16.故选C.
8.答案:B
解析:根据框图,执行程序,
;
;
……
,
令,
解得,即时结束程序,
所以,
故选:B.
9.答案:D
解析:第一次循环,不成立,,;
第二次循环,不成立,,;
以此类推,执行最后一次循环,不成立,,;成立,输出.
故选:D.
10.答案:ACD
解析:由,得,又,所以,故A正确;
因为,所以当时,,此时,故B错误;
,所以,故C正确;
又,所以,故D正确.
所以选
11.答案:A
解析:设,
由题可得,且,
由③得,
则有,
因为
所以,
故A选项正确;
上面已证,
因为不知道m的正负,
所以该式子的正负无法恒定.
故选A.
12.答案:9
解析:作出不等式组对应的平面区域如图:由,得表示斜率为,纵截距为的一组平行直线,平移直线,当直线经过点时,此时直线截距最大,z最大,此时.
13.答案:6
解析:由约束条件,画出可行域如图所示阴影部分:
将目标函数转化为,平移直线,
当直线经过点A时,直线在y轴上截距最小,此时,目标函数取得最小值,
由,解得,
所以,
所以目标函数的最小值为,
故答案为6.
14.答案:4
解析:本题主要考查线性规划.根据题中所给约束条件可作出可行域如图所示,目标函数可化为,当z最大时,直线在y轴上的截距最小,由图可知当直线过直线和直线的交点时,截距最小,联立,解得,此时,所以z最大值为4.故本题正确答案为4.
同课章节目录
