2021年高考数学真题模拟试题专项汇编之立体几何(理)(Word版,含解析)
文档属性
| 名称 | 2021年高考数学真题模拟试题专项汇编之立体几何(理)(Word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 10:12:32 | ||
图片预览



文档简介
(8)立体几何(理)——2021年高考数学真题模拟试题专项汇编
1.【2021年新高考Ⅰ卷,3】已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为(
)
A.2
B.
C.4
D.
2.【2021年新高考Ⅱ卷,4】卫星导航系统中,地球静止同步轨道卫星的轨道位于地球赤道所在平面,轨道高度为36000km(轨道高度指卫星到地球表面的最短距离).把地球看成一个球心为O,半径为6400km的球,其上点A的纬度是指OA与赤道所在平面所成角的度数,地球表面能直接观测到的一颗地球静止同步轨道卫星的点的纬度的最大值记为.该卫星信号覆盖的地球表面面积(单位:),则S占地球表面积的百分比为(
)
A.26%
B.34%
C.42%
D.50%
3.【2021年北京卷,4】某四面体的三视图如图所示,该四面体的表面积为(
)
A.
B.
C.
D.
4.【2021年新高考Ⅱ卷,5】正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则四棱台的体积为(
)
A.
B.
C.
D.
5.【2021年全国乙卷(理),5】在正方体中,P为的中点,则直线PB与所成的角为(
)
A.
B.
C.
D.
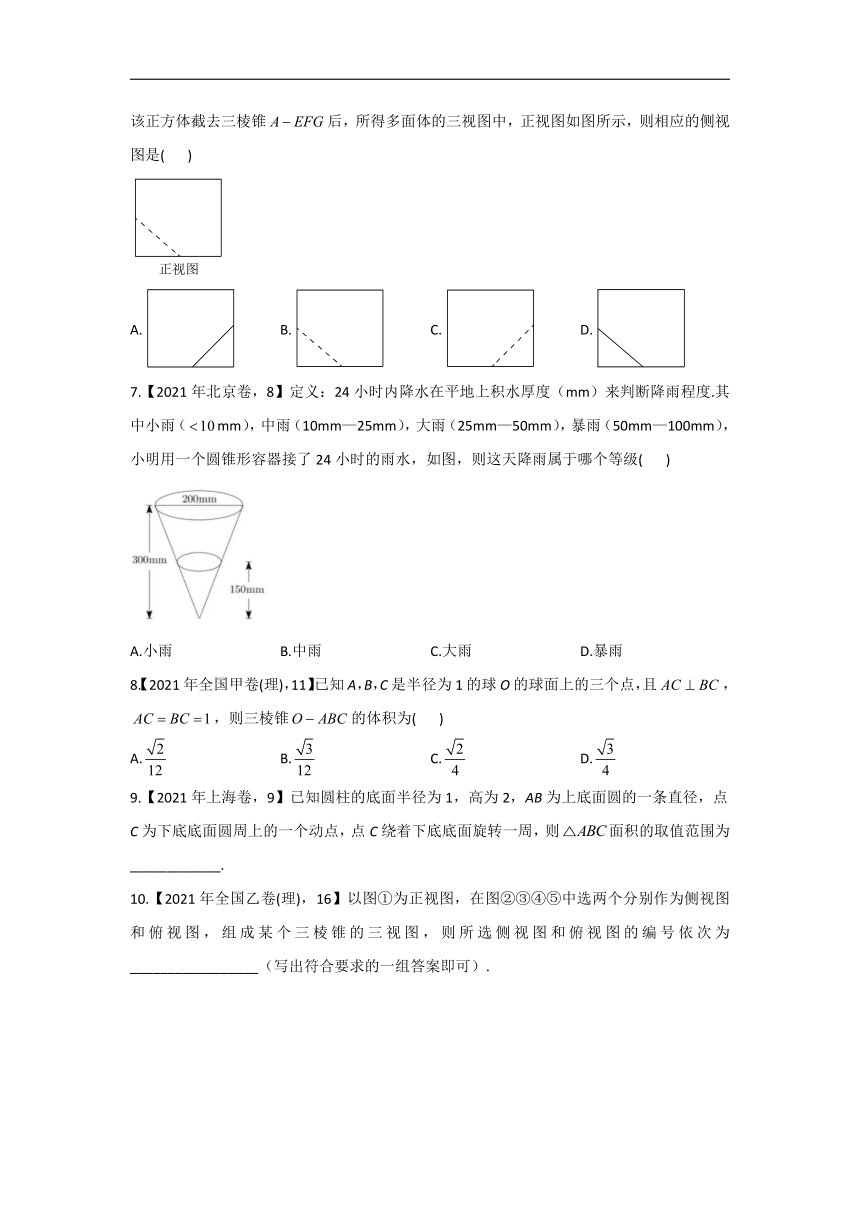
6.【2021年全国甲卷(理),6】在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是(
)
A.
B.
C.
D.
7.【2021年北京卷,8】定义:24小时内降水在平地上积水厚度(mm)来判断降雨程度.其中小雨(mm),中雨(10mm—25mm),大雨(25mm—50mm),暴雨(50mm—100mm),小明用一个圆锥形容器接了24小时的雨水,如图,则这天降雨属于哪个等级(
)
A.小雨
B.中雨
C.大雨
D.暴雨
8.【2021年全国甲卷(理),11】已知A,B,C是半径为1的球O的球面上的三个点,且,,则三棱锥的体积为(
)
A.
B.
C.
D.
9.【2021年上海卷,9】已知圆柱的底面半径为1,高为2,AB为上底面圆的一条直径,点C为下底底面圆周上的一个动点,点C绕着下底底面旋转一周,则面积的取值范围为____________.
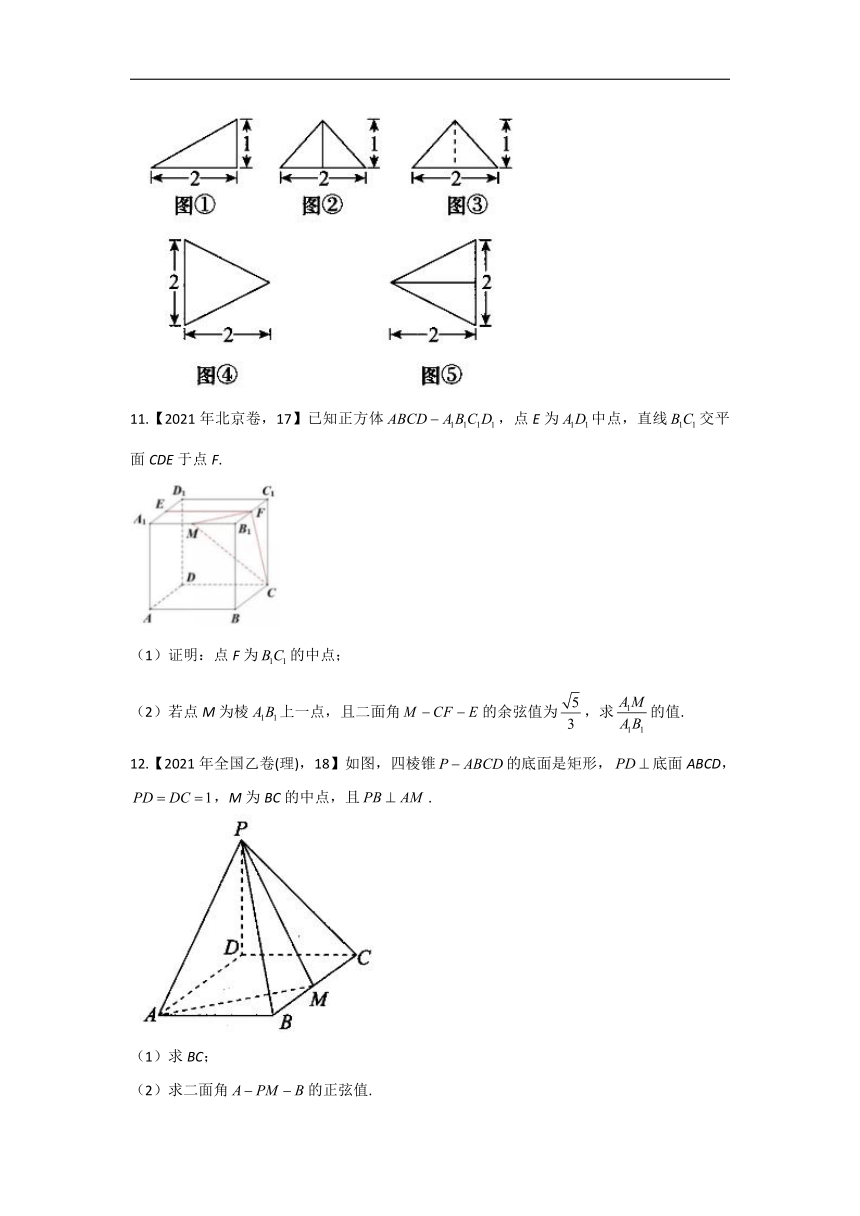
10.【2021年全国乙卷(理),16】以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________________(写出符合要求的一组答案即可).
11.【2021年北京卷,17】已知正方体,点E为中点,直线交平面CDE于点F.
(1)证明:点F为的中点;
(2)若点M为棱上一点,且二面角的余弦值为,求的值.
12.【2021年全国乙卷(理),18】如图,四棱锥的底面是矩形,底面ABCD,,M为BC的中点,且.
(1)求BC;
(2)求二面角的正弦值.
13.【2021年全国甲卷(理),19】已知直三棱柱中,侧面为正方形.,E,F分别为AC和的中点,D为棱上的点,.
(1)证明:;
(2)当为何值时,面与面DFE所成的二面角的正弦值最小?
14.【2021年新高考Ⅱ卷,19】在四棱锥中,底面ABCD是正方形,若,,.
(1)证明:平面平面ABCD;
(2)求二面角的平面角的余弦值.
15.【2021年新高考Ⅰ卷,20】如图,在三棱锥中,平面平面,,O为BD的中点.
(1)证明:;
(2)若是边长为1的等边三角形,点E在棱AD上,,且二面角的大小为,求三棱锥的体积.
答案以及解析
1.答案:B
解析:本题考查圆锥的侧面展开图.设圆锥的底面半径为r,母线长为l.由题意可得,所以.
2.答案:C
解析:由题意可知,,所以从同步卫星上可望见的地球的表面积,此面积与地球表面积之比约为.
3.答案:A
解析:画正方体,删点,剩下的4个点就是三棱锥的顶点,如图:
.
4.答案:D
解析:本题考查棱台的体积.将正四棱台补成四棱锥,作底面ABCD于点O,交平面于点,则棱台的体积.由题意,,易知,,,而,所以,则
,,所以棱台的体积.
5.答案:D
解析:本题考查立体几何中的线面关系及解三角形的应用.如图,记正方体的棱长为a,则,所以,.在中,由余弦定理得,所以.又因为,所以即为直线PB与所成的角,所以直线PB与所成的角为.
6.答案:D
解析:本题考查三视图.由正视图虚线可知所截为正方体的里面左下角,故侧视图为实线左下角.
7.答案:B
解析:由相似的性质可得,小圆锥的底面半径,故,积水厚度,属于中雨,故选B.
8.答案:A
解析:本题考查三棱锥和球.设AB的中点是,可知,又,则三棱锥的高是,故体积是.
9.答案:
解析:本题主要考查空间几何体.上顶面圆心记为O,下底面圆心记为,连接OC,过点C作,垂足为点M,则,根据题意,AB为定值2,所以的大小随着CM长短的变化而变化.当点M与点O重合时,,取得最大值,此时.当点M与点B重合时,CM取最小值2,此时.综上所述,的取值范围为.
10.答案:②⑤或③④
解析:本题考查几何题的三视图.由高度可知,侧视图只能为②或③.
当侧视图为②时,则该三棱锥的直观图如图1,平面平面ABC,,,,此时俯视图为⑤;当侧视图为③时,则该三棱锥的直观图如图2,平面ABC,,,,此时俯视图为④.
11.答案:(1)证明:连接,因为为正方体,所以,.
又因为平面,平面,所以平面.
因为平面平面,且平面CDEF,所以,所以,
所以,
又因为,所以四边形为平行四边形,四边形为平行四边形,
所以,而点E为中点,
所以,所以,所以点F为中点.
(2)因为为正方体,故DA,DC,两两垂直,
以D为坐标原点,分别以DA,DC,所在直线为x轴,y轴,z轴建立空间直角坐标系,
令正方体的棱长为2,设.
则,,,.
,,.
设平面CEF的法向量为,
则,即,
故,令,,
可取.
设平面CMF的法向量为,
则,即,
令,则,,
可取.
设二面角为θ,且θ为锐角,故,
解得,故.
12.答案:(1)连接BD.
因为底面ABCD,且平面ABCD,
所以.
又因为,,平面PBD,平面PBD,
所以平面PBD.
又平面PBD,所以,所以.
又,
所以,所以,
则,所以,解得.
(2)易知DA,DC,DP两两垂直,故以点D为坐标原点建立如图所示的空间直角坐标系,
则,,,,
所以,,,,
设平面AMP的法向量为,
则有即
令,则,,故.
设平面BMP的法向量为,
则有即
令,则,故,
所以,
设二面角的平面角为,
则,
所以二面角的正弦值为.
13.答案:(1)因为E,F分别是AC和的中点,侧面为正方形且,
所以,.
如图,连接AF,由,,得,于是,所以.由得,故以B为坐标原点,以AB,BC,所在直线分别为x,y,z轴建立空间直角坐标系Bxyz,
则,,,.
设,则,
于是.
所以,所以.
(2)易知面的一个法向量为.
设面DFE的法向量为,
则
又,,
所以令,得,,
于是,面DFE的一个法向量为,
所以.
设面与面DFE所成的二面角为,则,
故当时,面与面DFE所成的二面角的正弦值最小,为,即当时,面与面DFE所成的二面角的正弦值最小.
14.答案:(1)如图,取AD的中点E,连接EQ,EC.
因为,所以.
又因为在正方形ABCD中,,所以,,
此时,所以.
又,EC,平面ABCD,
所以平面ABCD.
因为平面QAD,所以平面平面ABCD.
(2)由(1)知平面ABCD,因此以点E为原点,建立如图所示的空间直角坐标系Exyz,则,,,,.
设平面BDQ的法向量,则即
取,得,则.
易知平面AQD的一个法向量,
则,由图可知二面角的平面角为锐角,
因此二面角的平面角的余弦值为.
15.答案:(1)因为,O为BD的中点,
所以.
因为平面ABD,
平面平面BCD且平面平面,
所以平面BCD,
所以.
(2)以O为坐标原点,OD为y轴,OA为z轴,垂直OD且过点O的直线为x轴建立如图所示的空间直角坐标系Oxyz,
有,,,设,则.
设为平面EBC的法向量.
因为,,
所以
所以
令,所以,,
所以.
因为平面BCD的法向量为,
所以,解得,
所以,
因为,所以,
所以.
1.【2021年新高考Ⅰ卷,3】已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为(
)
A.2
B.
C.4
D.
2.【2021年新高考Ⅱ卷,4】卫星导航系统中,地球静止同步轨道卫星的轨道位于地球赤道所在平面,轨道高度为36000km(轨道高度指卫星到地球表面的最短距离).把地球看成一个球心为O,半径为6400km的球,其上点A的纬度是指OA与赤道所在平面所成角的度数,地球表面能直接观测到的一颗地球静止同步轨道卫星的点的纬度的最大值记为.该卫星信号覆盖的地球表面面积(单位:),则S占地球表面积的百分比为(
)
A.26%
B.34%
C.42%
D.50%
3.【2021年北京卷,4】某四面体的三视图如图所示,该四面体的表面积为(
)
A.
B.
C.
D.
4.【2021年新高考Ⅱ卷,5】正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则四棱台的体积为(
)
A.
B.
C.
D.
5.【2021年全国乙卷(理),5】在正方体中,P为的中点,则直线PB与所成的角为(
)
A.
B.
C.
D.
6.【2021年全国甲卷(理),6】在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是(
)
A.
B.
C.
D.
7.【2021年北京卷,8】定义:24小时内降水在平地上积水厚度(mm)来判断降雨程度.其中小雨(mm),中雨(10mm—25mm),大雨(25mm—50mm),暴雨(50mm—100mm),小明用一个圆锥形容器接了24小时的雨水,如图,则这天降雨属于哪个等级(
)
A.小雨
B.中雨
C.大雨
D.暴雨
8.【2021年全国甲卷(理),11】已知A,B,C是半径为1的球O的球面上的三个点,且,,则三棱锥的体积为(
)
A.
B.
C.
D.
9.【2021年上海卷,9】已知圆柱的底面半径为1,高为2,AB为上底面圆的一条直径,点C为下底底面圆周上的一个动点,点C绕着下底底面旋转一周,则面积的取值范围为____________.
10.【2021年全国乙卷(理),16】以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________________(写出符合要求的一组答案即可).
11.【2021年北京卷,17】已知正方体,点E为中点,直线交平面CDE于点F.
(1)证明:点F为的中点;
(2)若点M为棱上一点,且二面角的余弦值为,求的值.
12.【2021年全国乙卷(理),18】如图,四棱锥的底面是矩形,底面ABCD,,M为BC的中点,且.
(1)求BC;
(2)求二面角的正弦值.
13.【2021年全国甲卷(理),19】已知直三棱柱中,侧面为正方形.,E,F分别为AC和的中点,D为棱上的点,.
(1)证明:;
(2)当为何值时,面与面DFE所成的二面角的正弦值最小?
14.【2021年新高考Ⅱ卷,19】在四棱锥中,底面ABCD是正方形,若,,.
(1)证明:平面平面ABCD;
(2)求二面角的平面角的余弦值.
15.【2021年新高考Ⅰ卷,20】如图,在三棱锥中,平面平面,,O为BD的中点.
(1)证明:;
(2)若是边长为1的等边三角形,点E在棱AD上,,且二面角的大小为,求三棱锥的体积.
答案以及解析
1.答案:B
解析:本题考查圆锥的侧面展开图.设圆锥的底面半径为r,母线长为l.由题意可得,所以.
2.答案:C
解析:由题意可知,,所以从同步卫星上可望见的地球的表面积,此面积与地球表面积之比约为.
3.答案:A
解析:画正方体,删点,剩下的4个点就是三棱锥的顶点,如图:
.
4.答案:D
解析:本题考查棱台的体积.将正四棱台补成四棱锥,作底面ABCD于点O,交平面于点,则棱台的体积.由题意,,易知,,,而,所以,则
,,所以棱台的体积.
5.答案:D
解析:本题考查立体几何中的线面关系及解三角形的应用.如图,记正方体的棱长为a,则,所以,.在中,由余弦定理得,所以.又因为,所以即为直线PB与所成的角,所以直线PB与所成的角为.
6.答案:D
解析:本题考查三视图.由正视图虚线可知所截为正方体的里面左下角,故侧视图为实线左下角.
7.答案:B
解析:由相似的性质可得,小圆锥的底面半径,故,积水厚度,属于中雨,故选B.
8.答案:A
解析:本题考查三棱锥和球.设AB的中点是,可知,又,则三棱锥的高是,故体积是.
9.答案:
解析:本题主要考查空间几何体.上顶面圆心记为O,下底面圆心记为,连接OC,过点C作,垂足为点M,则,根据题意,AB为定值2,所以的大小随着CM长短的变化而变化.当点M与点O重合时,,取得最大值,此时.当点M与点B重合时,CM取最小值2,此时.综上所述,的取值范围为.
10.答案:②⑤或③④
解析:本题考查几何题的三视图.由高度可知,侧视图只能为②或③.
当侧视图为②时,则该三棱锥的直观图如图1,平面平面ABC,,,,此时俯视图为⑤;当侧视图为③时,则该三棱锥的直观图如图2,平面ABC,,,,此时俯视图为④.
11.答案:(1)证明:连接,因为为正方体,所以,.
又因为平面,平面,所以平面.
因为平面平面,且平面CDEF,所以,所以,
所以,
又因为,所以四边形为平行四边形,四边形为平行四边形,
所以,而点E为中点,
所以,所以,所以点F为中点.
(2)因为为正方体,故DA,DC,两两垂直,
以D为坐标原点,分别以DA,DC,所在直线为x轴,y轴,z轴建立空间直角坐标系,
令正方体的棱长为2,设.
则,,,.
,,.
设平面CEF的法向量为,
则,即,
故,令,,
可取.
设平面CMF的法向量为,
则,即,
令,则,,
可取.
设二面角为θ,且θ为锐角,故,
解得,故.
12.答案:(1)连接BD.
因为底面ABCD,且平面ABCD,
所以.
又因为,,平面PBD,平面PBD,
所以平面PBD.
又平面PBD,所以,所以.
又,
所以,所以,
则,所以,解得.
(2)易知DA,DC,DP两两垂直,故以点D为坐标原点建立如图所示的空间直角坐标系,
则,,,,
所以,,,,
设平面AMP的法向量为,
则有即
令,则,,故.
设平面BMP的法向量为,
则有即
令,则,故,
所以,
设二面角的平面角为,
则,
所以二面角的正弦值为.
13.答案:(1)因为E,F分别是AC和的中点,侧面为正方形且,
所以,.
如图,连接AF,由,,得,于是,所以.由得,故以B为坐标原点,以AB,BC,所在直线分别为x,y,z轴建立空间直角坐标系Bxyz,
则,,,.
设,则,
于是.
所以,所以.
(2)易知面的一个法向量为.
设面DFE的法向量为,
则
又,,
所以令,得,,
于是,面DFE的一个法向量为,
所以.
设面与面DFE所成的二面角为,则,
故当时,面与面DFE所成的二面角的正弦值最小,为,即当时,面与面DFE所成的二面角的正弦值最小.
14.答案:(1)如图,取AD的中点E,连接EQ,EC.
因为,所以.
又因为在正方形ABCD中,,所以,,
此时,所以.
又,EC,平面ABCD,
所以平面ABCD.
因为平面QAD,所以平面平面ABCD.
(2)由(1)知平面ABCD,因此以点E为原点,建立如图所示的空间直角坐标系Exyz,则,,,,.
设平面BDQ的法向量,则即
取,得,则.
易知平面AQD的一个法向量,
则,由图可知二面角的平面角为锐角,
因此二面角的平面角的余弦值为.
15.答案:(1)因为,O为BD的中点,
所以.
因为平面ABD,
平面平面BCD且平面平面,
所以平面BCD,
所以.
(2)以O为坐标原点,OD为y轴,OA为z轴,垂直OD且过点O的直线为x轴建立如图所示的空间直角坐标系Oxyz,
有,,,设,则.
设为平面EBC的法向量.
因为,,
所以
所以
令,所以,,
所以.
因为平面BCD的法向量为,
所以,解得,
所以,
因为,所以,
所以.
同课章节目录
