2021-2022学年北师大版五年级数学上册《第四单元 多边形的面积》单元测试题(word版,含答案)
文档属性
| 名称 | 2021-2022学年北师大版五年级数学上册《第四单元 多边形的面积》单元测试题(word版,含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 00:00:00 | ||
图片预览

文档简介
2021-2022学年北师大版五年级数学上册《第四单元
多边形的面积》单元测试题
一.选择题(共8小题,共16分)
1.如图中每小格边长1厘米,其中( )是三角形面积的2倍.
A.A
B.B
C.C
D.D
2.下面说法正确的是( )
A.周长相等的梯形面积相等
B.从不同方向看一个物体,看到的肯定不同
C.平行四边形的底不变,高扩大2倍,面积就扩大4倍
D.甲数(大于0)乘a(大于1),积大于甲数
3.已知一条直线l和直线外的A、B两点,以A、B两点和直线上某一点做为三角形的三个顶点,就能画出一个等腰三角形,如图中的等腰三角形ABC.除此之外还能画出符合条件的( )个等腰三角形.
A.1
B.2
C.4
4.一堆圆木,堆成梯形状,下层12根,上层7根,共堆有6层,这堆圆木共有( )根.
A.57
B.50
C.76
D.45
5.爷爷家原来有一个宽9米,面积306平方米的鱼塘,扩建后,长不变,宽增加到18米,扩建后的鱼塘面积是( )平方米。
A.153
B.612
C.702
D.2754
6.把一个长方形框对角拉成平行四边形,在这个过程中,下列说法正确的是( )
A.拉动后面积发生变化,周长不变
B.拉动后周长发生变化,面积不变
C.拉动后周长和面积都发生变化
D.拉动后周长和面积都没有发生变化
7.(如图)一个长方形框架拉成平行四边形后,面积是24dm2,面积比原来减少了( )dm2。
A.8
B.16
C.24
D.32
8.如图中有( )个三角形的面积可以用算式“4×3÷2”进行计算。
A.1
B.2
C.3
D.4
二.填空题(共10小题,共16分)
9.一块长方形草坪(如图),长不变,宽增加到28米,扩大后这块绿地的面积是
平方米。
10.将一个梯形分成等底等高的平行四边形和三角形(如图),已知三角形的面积是1.2cm2,平行四边形的底是1.5cm,这个梯形的高是
cm,梯形的面积是
cm2.
11.在右面直角三角形中,∠1+∠2=
,如果这个直角三角形的两条直角边的长分别是4cm、5cm,那么它的面积是
cm2。
12.一个三角形的底是6厘米,高是4.5厘米,这个三角形的面积是
平方厘米。
13.平行四边形的面积=
×
,如果底是5cm,高是12cm,那么这个平行四边形的面积是
cm2。
14.一个长方形的宽是7厘米,宽增加2厘米,面积是144平方厘米。原来长方形的面积是
平方厘米。
15.在平行四边形ABCD中(如图),AB边上的高是
cm,BC边上的高是
cm。
16.在给定的正方形方格顶点上找一点C,使这一点和线段AB围成的三角形的面积是2平方厘米,点C共有
种不同的画法.(每个小方格表示1平方厘米)
17.已知梯形的下底长是上底长的2倍,高为5厘米,面积为15平方厘米,那么梯形的上底长是
厘米.
18.一个平行四边形,沿它任意一条高剪开,通过平移拼成长方形。这个长方形的长与原来平行四边形的
相等;原平行四边形的高与长方形的
相等。
三.判断题(共5小题,共10分)
19.两个三角形的底和高分别相等,这两个三角形的面积也一定相等。
(判断对错)
20.一个边长5厘米的正方形,面积和周长相等。
(判断对错)
21.梯形的面积是平行四边形面积的一半.
.(判断对错)
22.用割补法把平行四边形转化成长方形后,面积和周长都没有改变。
(判断对错)
23.梯形的上、下底不变,高扩大为原来的2倍,面积也扩大为原来的2倍.
(判断对错)
四.计算题(共2小题,共12分)
24.计算图形的面积.
25.求阴影部分面积。(单位:cm)
五.操作题(共1小题,共6分)
26.在边长为1厘米的方格图中画一个平行四边形和一个梯形,使它们的面积都等于8平方厘米.
六.应用题(共5小题,共40分)
27.用一条40厘米长的铁丝围成一个等腰三角形,它的底边长是14厘米,它的一条腰长是多少厘米?
28.某人民医院用一块长60m、宽0.8m的白布做成底和高都是0.4m的包扎三角巾,一共可以做多少块?
29.体育馆准备修建游泳池.如果将长增加20米,或者宽增加5米,那么面积都比原来增加400平方米(如图).原来游泳池占地多少平方米?
30.果园里有一块平行四边形的地,底是120米,高是60米,如果每棵苹果树占地24平方米,这块地可栽多少棵苹果树?
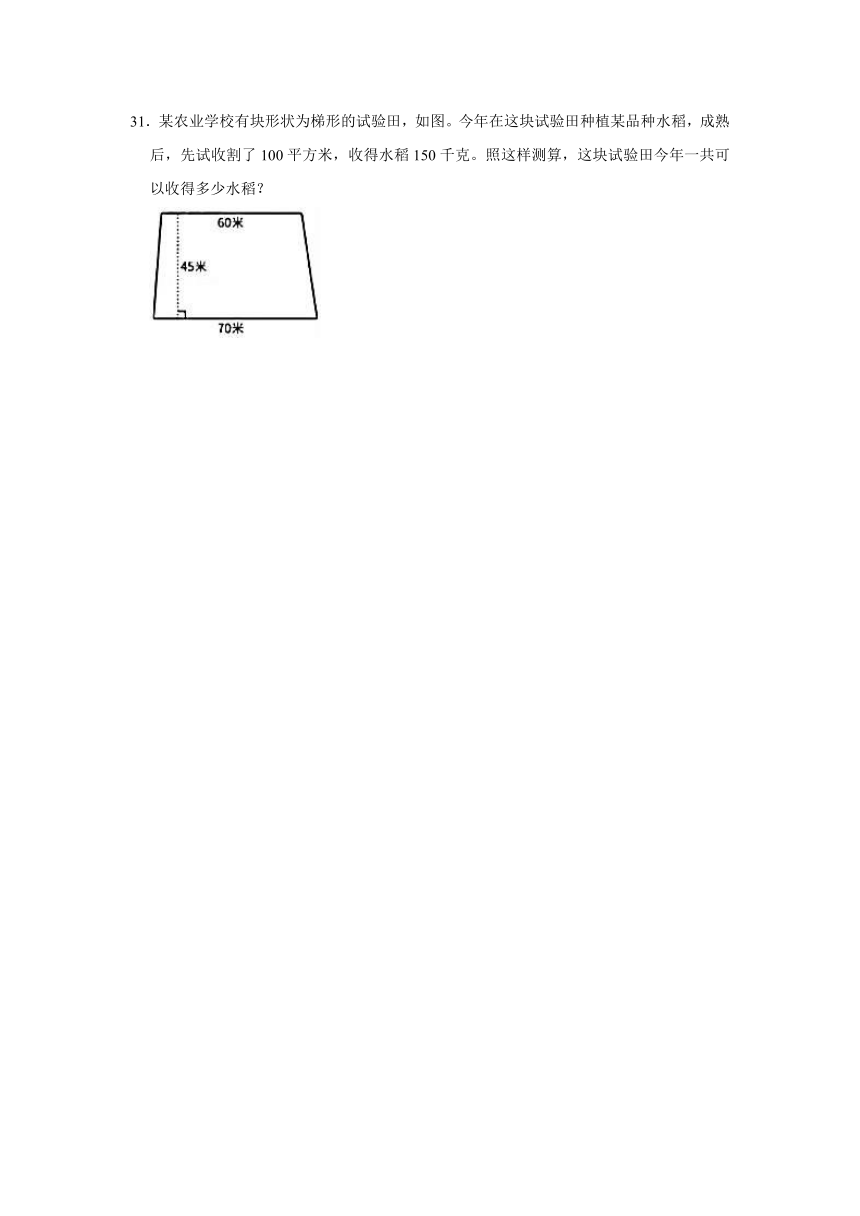
31.某农业学校有块形状为梯形的试验田,如图。今年在这块试验田种植某品种水稻,成熟后,先试收割了100平方米,收得水稻150千克。照这样测算,这块试验田今年一共可以收得多少水稻?
参考答案与试题解析
一.选择题(共8小题)
1.解:三角形的面积:3×3÷2=4.5(平方厘米)
三角形面积的2倍是:4.5×2=9(平方厘米)
A的面积:(1+4)×3÷2=7.5(平方厘米)
B的面积:3×2=6(平方厘米)
C的面积:3×3=9(平方厘米)
D的面积:(2+3)×3÷2=7.5(平方厘米)
故选:C.
2.解:A、周长相等的梯形,上下底和高不一定相等,所以面积就不一定相等,原题说法错误;
B、从不同方向看一个正方体,则看到的都是正方形,所以原题说法错误;
C、平行四边形的底不变,高扩大2倍,面积就扩大2倍,所以原题说法错误;
D、甲数(大于0)乘a(大于1),积大于甲数;说法正确.
故选:D.
3.解:(1)分别是做AB的垂直平分线,与直线的交点是C点,可做等腰三角形;
(2)以AB为半径,以A点为圆心画圆,与直线有两个交点,分别是C1、C2.这两点均可作为符合条件的C点;
(3)同样,以AB为半径,以B点为圆心画圆,与直线交的两个点也符合条件,其中一个就是图上的C点;
答:除此之外还能画出符合条件的4个等腰三角形.
故选:C.
4.解:(12+7)×6÷2,
=19×6÷2,
=57(根).
故选:A.
5.解:306÷9×18
=34×18
=612(平方米)
答:扩建后的鱼塘面积是612平方米。
故选:B。
6.解;用木条钉成一个长方形框,沿对角线拉成一个平行四边形。这个平行四边形与原来的长方形相比周长不变,拉成的平行四边形的高小于长方形的宽,所以面积变小了。
故选:A。
7.解:24÷3=8(分米)
8×4﹣24
=32﹣24
=8(平方分米)
答:面积减少了8平方分米。
故选:A。
8.解:图(1)和图(2)底对应的高都是3厘米,所以图(1)和图(2)的面积可以用“4×3÷2”进行计算。
所以,图中有2个三角形的面积可以用算式“4×3÷2”进行计算。
故选:B。
二.填空题(共10小题)
9.解:392÷14=28(米)
28×28=784(平方米)
答:扩大后这块绿地的面积是784平方米。
故答案为:784。
10.解:1.2×2÷1.5
=2.4÷1.5
=1.6(厘米)
1.2+1.2×2
=1.2+2.4
=3.6(平方厘米)
答:这个梯形的高是1.6厘米,面积是3.6平方厘米.
故答案为:1.6、3.6.
11.解:∠1+∠2=180°﹣90°=90°
5×4÷2=10(平方厘米)
它的面积是10平方厘米。
故答案为:90°;10。
12.解:6×4.5÷2=13.5(平方厘米)
答:这个三角形面积是13.5平方厘米。
故答案为:13.5。
13.解:5×12=60(平方厘米)
答:平行四边形的面积=底×高,如果底是5cm,高是12cm,那么这个平行四边形的面积是60平方厘米。
故答案为:底;高;60。
14.解:144÷(7+2)
=144÷9
=16(厘米)
16×7=112(平方厘米)
答:原来长方形的面积是112平方厘米。
故答案为:112。
15.解:AB边上的高是6厘米,BC边上的高是9厘米。
故答案为:6、9。
16.解:三角形的高:2×2÷2=2(厘米)
因为这个方格图是边长5厘米的大正方形,所以C点共有10种不同的画法.
故答案为:10.
17.解:15×2÷5÷(2+1)
=30÷5÷3
=6÷3
=2(厘米)
答:梯形的上底是2厘米。
故答案为:2。
18.解:一个平行四边形,沿它任意一条高剪开,通过平移拼成长方形。这个长方形的长与原来平行四边形的底相等,原来平行四边形的高与长方形的宽相等。拼成的长方形的面积等于平行四边形的面积。
故答案为:底、宽。
三.判断题(共5小题)
19.解:三角形的面积=底×高÷2,
底和高分别相等的两个三角形,它们的底和高的乘积相等,则它们的面积一定相等;
原题说法正确。
故答案为:√。
20.解:因为周长和面积不是同类量,所以无法进行比较。
因此,一个边长5厘米的正方形,面积和周长相等。此说法错误。
故答案为:×。
21.解:等底等高的梯形的面积是平行四边形面积的一半,
原题缺少关键词“等底等高”,所以说法错误.
故答案为:×.
22.解:由分析可知,一个平行四边形转化成一个长方形时,面积不变,周长变小。
因此,用割补法把平行四边形转化成长方形后,面积和周长都没有改变。这种说法是错误的。
故答案为:×。
23.解:一个因数不变,另一个因数扩大到原来的2倍,积也扩大到原来的2倍。
因此,梯形的上、下底不变,高扩大为原来的2倍,面积也扩大为原来的2倍。这种说法是正确的。
故答案为:√。
四.计算题(共2小题)
24.解:40×30=1200(平方分米)
答:这个平行四边形的面积是1200平方分米。
25.解:(3+3+8)×5÷2
=14×5÷2
=70÷2
=35(平方厘米)
答:阴影部分的面积是35平方厘米。
五.操作题(共1小题)
26.解:因为S平行四边形=S梯形=8平方厘米,
平行四边形的底和高为4厘米和2厘米,
梯形的上底、下底和高分为3厘米、5厘米和2厘米,
六.应用题(共5小题)
27.解:(40﹣14)÷2
=26÷2
=13(厘米)
答:它的一条腰长是13厘米。
28.解:60×0.8÷(0.4×0.4÷2)
=48÷0.08
=600(块)
答:一共可以做600块。
29.解:(400÷5)×(400÷20)
=80×20
=1600(平方米)
答:原来游泳池占地1600平方米.
30.解:120×60÷24
=7200÷24
=300(棵)
答:这块地可栽300棵苹果树。
31.解:(150÷100)×[(60+70)×45÷2]
=1.5×[130×45÷2]
=1.5×2925
=4387.5(千克)
答:这块试验田今年一共可以收4387.5千克水稻。
多边形的面积》单元测试题
一.选择题(共8小题,共16分)
1.如图中每小格边长1厘米,其中( )是三角形面积的2倍.
A.A
B.B
C.C
D.D
2.下面说法正确的是( )
A.周长相等的梯形面积相等
B.从不同方向看一个物体,看到的肯定不同
C.平行四边形的底不变,高扩大2倍,面积就扩大4倍
D.甲数(大于0)乘a(大于1),积大于甲数
3.已知一条直线l和直线外的A、B两点,以A、B两点和直线上某一点做为三角形的三个顶点,就能画出一个等腰三角形,如图中的等腰三角形ABC.除此之外还能画出符合条件的( )个等腰三角形.
A.1
B.2
C.4
4.一堆圆木,堆成梯形状,下层12根,上层7根,共堆有6层,这堆圆木共有( )根.
A.57
B.50
C.76
D.45
5.爷爷家原来有一个宽9米,面积306平方米的鱼塘,扩建后,长不变,宽增加到18米,扩建后的鱼塘面积是( )平方米。
A.153
B.612
C.702
D.2754
6.把一个长方形框对角拉成平行四边形,在这个过程中,下列说法正确的是( )
A.拉动后面积发生变化,周长不变
B.拉动后周长发生变化,面积不变
C.拉动后周长和面积都发生变化
D.拉动后周长和面积都没有发生变化
7.(如图)一个长方形框架拉成平行四边形后,面积是24dm2,面积比原来减少了( )dm2。
A.8
B.16
C.24
D.32
8.如图中有( )个三角形的面积可以用算式“4×3÷2”进行计算。
A.1
B.2
C.3
D.4
二.填空题(共10小题,共16分)
9.一块长方形草坪(如图),长不变,宽增加到28米,扩大后这块绿地的面积是
平方米。
10.将一个梯形分成等底等高的平行四边形和三角形(如图),已知三角形的面积是1.2cm2,平行四边形的底是1.5cm,这个梯形的高是
cm,梯形的面积是
cm2.
11.在右面直角三角形中,∠1+∠2=
,如果这个直角三角形的两条直角边的长分别是4cm、5cm,那么它的面积是
cm2。
12.一个三角形的底是6厘米,高是4.5厘米,这个三角形的面积是
平方厘米。
13.平行四边形的面积=
×
,如果底是5cm,高是12cm,那么这个平行四边形的面积是
cm2。
14.一个长方形的宽是7厘米,宽增加2厘米,面积是144平方厘米。原来长方形的面积是
平方厘米。
15.在平行四边形ABCD中(如图),AB边上的高是
cm,BC边上的高是
cm。
16.在给定的正方形方格顶点上找一点C,使这一点和线段AB围成的三角形的面积是2平方厘米,点C共有
种不同的画法.(每个小方格表示1平方厘米)
17.已知梯形的下底长是上底长的2倍,高为5厘米,面积为15平方厘米,那么梯形的上底长是
厘米.
18.一个平行四边形,沿它任意一条高剪开,通过平移拼成长方形。这个长方形的长与原来平行四边形的
相等;原平行四边形的高与长方形的
相等。
三.判断题(共5小题,共10分)
19.两个三角形的底和高分别相等,这两个三角形的面积也一定相等。
(判断对错)
20.一个边长5厘米的正方形,面积和周长相等。
(判断对错)
21.梯形的面积是平行四边形面积的一半.
.(判断对错)
22.用割补法把平行四边形转化成长方形后,面积和周长都没有改变。
(判断对错)
23.梯形的上、下底不变,高扩大为原来的2倍,面积也扩大为原来的2倍.
(判断对错)
四.计算题(共2小题,共12分)
24.计算图形的面积.
25.求阴影部分面积。(单位:cm)
五.操作题(共1小题,共6分)
26.在边长为1厘米的方格图中画一个平行四边形和一个梯形,使它们的面积都等于8平方厘米.
六.应用题(共5小题,共40分)
27.用一条40厘米长的铁丝围成一个等腰三角形,它的底边长是14厘米,它的一条腰长是多少厘米?
28.某人民医院用一块长60m、宽0.8m的白布做成底和高都是0.4m的包扎三角巾,一共可以做多少块?
29.体育馆准备修建游泳池.如果将长增加20米,或者宽增加5米,那么面积都比原来增加400平方米(如图).原来游泳池占地多少平方米?
30.果园里有一块平行四边形的地,底是120米,高是60米,如果每棵苹果树占地24平方米,这块地可栽多少棵苹果树?
31.某农业学校有块形状为梯形的试验田,如图。今年在这块试验田种植某品种水稻,成熟后,先试收割了100平方米,收得水稻150千克。照这样测算,这块试验田今年一共可以收得多少水稻?
参考答案与试题解析
一.选择题(共8小题)
1.解:三角形的面积:3×3÷2=4.5(平方厘米)
三角形面积的2倍是:4.5×2=9(平方厘米)
A的面积:(1+4)×3÷2=7.5(平方厘米)
B的面积:3×2=6(平方厘米)
C的面积:3×3=9(平方厘米)
D的面积:(2+3)×3÷2=7.5(平方厘米)
故选:C.
2.解:A、周长相等的梯形,上下底和高不一定相等,所以面积就不一定相等,原题说法错误;
B、从不同方向看一个正方体,则看到的都是正方形,所以原题说法错误;
C、平行四边形的底不变,高扩大2倍,面积就扩大2倍,所以原题说法错误;
D、甲数(大于0)乘a(大于1),积大于甲数;说法正确.
故选:D.
3.解:(1)分别是做AB的垂直平分线,与直线的交点是C点,可做等腰三角形;
(2)以AB为半径,以A点为圆心画圆,与直线有两个交点,分别是C1、C2.这两点均可作为符合条件的C点;
(3)同样,以AB为半径,以B点为圆心画圆,与直线交的两个点也符合条件,其中一个就是图上的C点;
答:除此之外还能画出符合条件的4个等腰三角形.
故选:C.
4.解:(12+7)×6÷2,
=19×6÷2,
=57(根).
故选:A.
5.解:306÷9×18
=34×18
=612(平方米)
答:扩建后的鱼塘面积是612平方米。
故选:B。
6.解;用木条钉成一个长方形框,沿对角线拉成一个平行四边形。这个平行四边形与原来的长方形相比周长不变,拉成的平行四边形的高小于长方形的宽,所以面积变小了。
故选:A。
7.解:24÷3=8(分米)
8×4﹣24
=32﹣24
=8(平方分米)
答:面积减少了8平方分米。
故选:A。
8.解:图(1)和图(2)底对应的高都是3厘米,所以图(1)和图(2)的面积可以用“4×3÷2”进行计算。
所以,图中有2个三角形的面积可以用算式“4×3÷2”进行计算。
故选:B。
二.填空题(共10小题)
9.解:392÷14=28(米)
28×28=784(平方米)
答:扩大后这块绿地的面积是784平方米。
故答案为:784。
10.解:1.2×2÷1.5
=2.4÷1.5
=1.6(厘米)
1.2+1.2×2
=1.2+2.4
=3.6(平方厘米)
答:这个梯形的高是1.6厘米,面积是3.6平方厘米.
故答案为:1.6、3.6.
11.解:∠1+∠2=180°﹣90°=90°
5×4÷2=10(平方厘米)
它的面积是10平方厘米。
故答案为:90°;10。
12.解:6×4.5÷2=13.5(平方厘米)
答:这个三角形面积是13.5平方厘米。
故答案为:13.5。
13.解:5×12=60(平方厘米)
答:平行四边形的面积=底×高,如果底是5cm,高是12cm,那么这个平行四边形的面积是60平方厘米。
故答案为:底;高;60。
14.解:144÷(7+2)
=144÷9
=16(厘米)
16×7=112(平方厘米)
答:原来长方形的面积是112平方厘米。
故答案为:112。
15.解:AB边上的高是6厘米,BC边上的高是9厘米。
故答案为:6、9。
16.解:三角形的高:2×2÷2=2(厘米)
因为这个方格图是边长5厘米的大正方形,所以C点共有10种不同的画法.
故答案为:10.
17.解:15×2÷5÷(2+1)
=30÷5÷3
=6÷3
=2(厘米)
答:梯形的上底是2厘米。
故答案为:2。
18.解:一个平行四边形,沿它任意一条高剪开,通过平移拼成长方形。这个长方形的长与原来平行四边形的底相等,原来平行四边形的高与长方形的宽相等。拼成的长方形的面积等于平行四边形的面积。
故答案为:底、宽。
三.判断题(共5小题)
19.解:三角形的面积=底×高÷2,
底和高分别相等的两个三角形,它们的底和高的乘积相等,则它们的面积一定相等;
原题说法正确。
故答案为:√。
20.解:因为周长和面积不是同类量,所以无法进行比较。
因此,一个边长5厘米的正方形,面积和周长相等。此说法错误。
故答案为:×。
21.解:等底等高的梯形的面积是平行四边形面积的一半,
原题缺少关键词“等底等高”,所以说法错误.
故答案为:×.
22.解:由分析可知,一个平行四边形转化成一个长方形时,面积不变,周长变小。
因此,用割补法把平行四边形转化成长方形后,面积和周长都没有改变。这种说法是错误的。
故答案为:×。
23.解:一个因数不变,另一个因数扩大到原来的2倍,积也扩大到原来的2倍。
因此,梯形的上、下底不变,高扩大为原来的2倍,面积也扩大为原来的2倍。这种说法是正确的。
故答案为:√。
四.计算题(共2小题)
24.解:40×30=1200(平方分米)
答:这个平行四边形的面积是1200平方分米。
25.解:(3+3+8)×5÷2
=14×5÷2
=70÷2
=35(平方厘米)
答:阴影部分的面积是35平方厘米。
五.操作题(共1小题)
26.解:因为S平行四边形=S梯形=8平方厘米,
平行四边形的底和高为4厘米和2厘米,
梯形的上底、下底和高分为3厘米、5厘米和2厘米,
六.应用题(共5小题)
27.解:(40﹣14)÷2
=26÷2
=13(厘米)
答:它的一条腰长是13厘米。
28.解:60×0.8÷(0.4×0.4÷2)
=48÷0.08
=600(块)
答:一共可以做600块。
29.解:(400÷5)×(400÷20)
=80×20
=1600(平方米)
答:原来游泳池占地1600平方米.
30.解:120×60÷24
=7200÷24
=300(棵)
答:这块地可栽300棵苹果树。
31.解:(150÷100)×[(60+70)×45÷2]
=1.5×[130×45÷2]
=1.5×2925
=4387.5(千克)
答:这块试验田今年一共可以收4387.5千克水稻。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
