2021-2022学年苏科版数学八年级上册3.3勾股定理的简单应用 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级上册3.3勾股定理的简单应用 同步练习(word版含答案) | 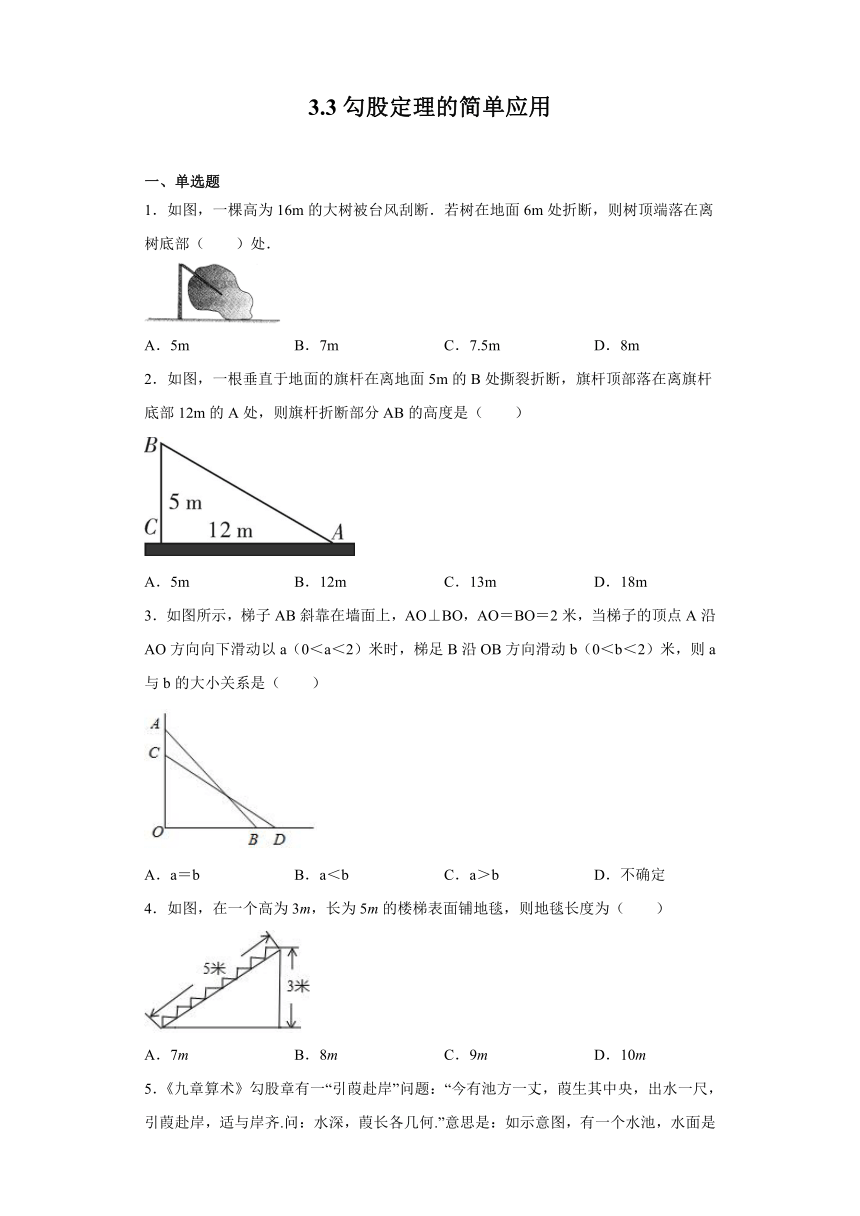 | |
| 格式 | docx | ||
| 文件大小 | 262.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 15:45:30 | ||
图片预览


文档简介
3.3勾股定理的简单应用
一、单选题
1.如图,一棵高为16m的大树被台风刮断.若树在地面6m处折断,则树顶端落在离树底部(
)处.
A.5m
B.7m
C.7.5m
D.8m
2.如图,一根垂直于地面的旗杆在离地面5m的B处撕裂折断,旗杆顶部落在离旗杆底部12m的A处,则旗杆折断部分AB的高度是(
)
A.5m
B.12m
C.13m
D.18m
3.如图所示,梯子AB斜靠在墙面上,AO⊥BO,AO=BO=2米,当梯子的顶点A沿AO方向向下滑动以a(0<a<2)米时,梯足B沿OB方向滑动b(0<b<2)米,则a与b的大小关系是( )
A.a=b
B.a<b
C.a>b
D.不确定
4.如图,在一个高为3m,长为5m的楼梯表面铺地毯,则地毯长度为( )
A.7m
B.8m
C.9m
D.10m
5.《九章算术》勾股章有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深,葭长各几何.”意思是:如示意图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度和芦苇的长度分别是多少?备注:1丈=10尺.设芦苇长尺,则可列方程为(
)
A.
B.
C.
D.
6.小明同学先向北行进千米,然后向东进千米,再向北行进千米,最后又向东行进一定距离,此时小明离出发点的距离是千米,小明最后向东行进了(
)
A.3千米
B.4千米
C.5千米
D.6千米
7.如图是一圆柱玻璃杯,从内部测得底面半径为
6cm,高为
16cm,现有一根长为
25cm
的吸管任意放入杯中,则吸管露在杯口外的长度最少是(
)
A.6cm
B.5cm
C.9cm
D.
cm
8.如图,一艘轮船位于灯塔的北偏东方向,与灯塔的距离为海里的处,轮船沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,则此时轮船所在位置处与灯塔之间的距离为(
)
A.60
海里
B.45海里
C.20海里
D.30海里
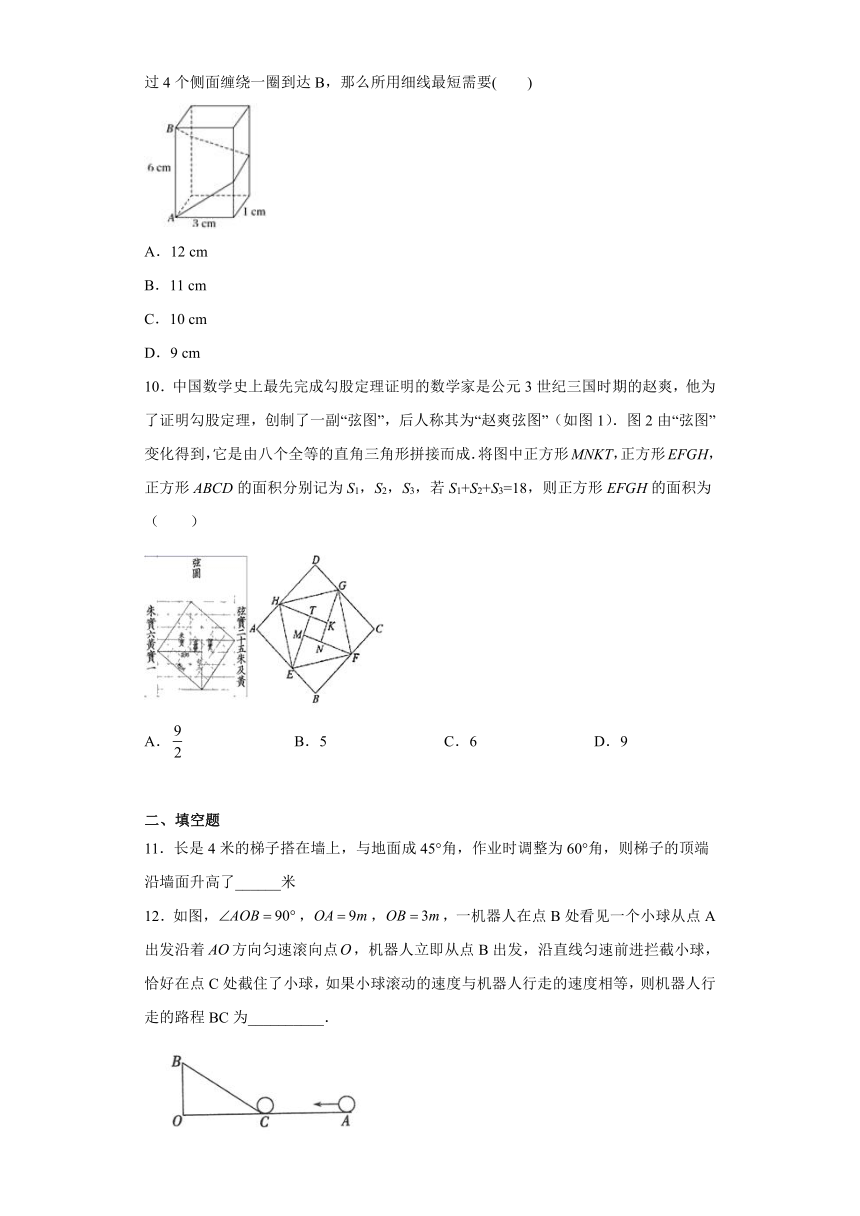
9.如图,长方体的底面边长为1
cm和3
cm,高为6
cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达B,那么所用细线最短需要( )
A.12
cm
B.11
cm
C.10
cm
D.9
cm
10.中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由“弦图”变化得到,它是由八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为(
)
A.
B.5
C.6
D.9
二、填空题
11.长是4米的梯子搭在墙上,与地面成45°角,作业时调整为60°角,则梯子的顶端沿墙面升高了______米
12.如图,,,,一机器人在点B处看见一个小球从点A出发沿着方向匀速滚向点,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC为__________.
13.一艘轮船在小岛的北偏东方向距小岛海里的处,沿正西方向航行小时后到达小岛的北偏西的处,则该船行驶的速度为_____海里/小时.
14.如图,有一个三级台阶,它的每一级的长,
宽和高分别是,,,点和点是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶表面爬到点的最短路程是____.
15.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为__________海里.
三、解答题
16.如图,某人为了测量小山顶上的塔顶离地面的高度,他在山下的点A处测得塔尖点D的仰角为,再沿方向前进到达山脚点B,测得塔尖点D的仰角为,求的高度(结果保留根号)
17.如图,星期天小明去钓鱼,鱼钩在离水面的的1.3米处,在距离鱼线1.2米处点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2米/秒的速度向鱼饵游去,那么这条鱼至少几秒后才能到达鱼饵处?
18.台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点
C为一海港,且点
C与直线AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有
小时.
参考答案
1.D
2.C
3.C
4.A
5.B
6.B
7.B
8.D
9.C
10.C
11.
12.5m
13.
14.20
15.
16.
17.6.5
18.(1)海港C受台风影响.
理由:如图,过点C作CD⊥AB于D,
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
∴AC?BC=CD?AB
∴CD=240(km)
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C受到台风影响.
(2)当EC=250km,FC=250km时,正好影响C港口,
∵ED==70(km)
∴EF=140km
∵台风的速度为20km/h,
∴140÷20=7(小时)
即台风影响该海港持续的时间为7小时.
故答案为:7.
一、单选题
1.如图,一棵高为16m的大树被台风刮断.若树在地面6m处折断,则树顶端落在离树底部(
)处.
A.5m
B.7m
C.7.5m
D.8m
2.如图,一根垂直于地面的旗杆在离地面5m的B处撕裂折断,旗杆顶部落在离旗杆底部12m的A处,则旗杆折断部分AB的高度是(
)
A.5m
B.12m
C.13m
D.18m
3.如图所示,梯子AB斜靠在墙面上,AO⊥BO,AO=BO=2米,当梯子的顶点A沿AO方向向下滑动以a(0<a<2)米时,梯足B沿OB方向滑动b(0<b<2)米,则a与b的大小关系是( )
A.a=b
B.a<b
C.a>b
D.不确定
4.如图,在一个高为3m,长为5m的楼梯表面铺地毯,则地毯长度为( )
A.7m
B.8m
C.9m
D.10m
5.《九章算术》勾股章有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深,葭长各几何.”意思是:如示意图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度和芦苇的长度分别是多少?备注:1丈=10尺.设芦苇长尺,则可列方程为(
)
A.
B.
C.
D.
6.小明同学先向北行进千米,然后向东进千米,再向北行进千米,最后又向东行进一定距离,此时小明离出发点的距离是千米,小明最后向东行进了(
)
A.3千米
B.4千米
C.5千米
D.6千米
7.如图是一圆柱玻璃杯,从内部测得底面半径为
6cm,高为
16cm,现有一根长为
25cm
的吸管任意放入杯中,则吸管露在杯口外的长度最少是(
)
A.6cm
B.5cm
C.9cm
D.
cm
8.如图,一艘轮船位于灯塔的北偏东方向,与灯塔的距离为海里的处,轮船沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,则此时轮船所在位置处与灯塔之间的距离为(
)
A.60
海里
B.45海里
C.20海里
D.30海里
9.如图,长方体的底面边长为1
cm和3
cm,高为6
cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达B,那么所用细线最短需要( )
A.12
cm
B.11
cm
C.10
cm
D.9
cm
10.中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由“弦图”变化得到,它是由八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为(
)
A.
B.5
C.6
D.9
二、填空题
11.长是4米的梯子搭在墙上,与地面成45°角,作业时调整为60°角,则梯子的顶端沿墙面升高了______米
12.如图,,,,一机器人在点B处看见一个小球从点A出发沿着方向匀速滚向点,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC为__________.
13.一艘轮船在小岛的北偏东方向距小岛海里的处,沿正西方向航行小时后到达小岛的北偏西的处,则该船行驶的速度为_____海里/小时.
14.如图,有一个三级台阶,它的每一级的长,
宽和高分别是,,,点和点是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶表面爬到点的最短路程是____.
15.如图,在一次测绘活动中,在港口A的位置观测停放于B、C两处的小船,测得船B在港口A北偏东75°方向12海里处,船C在港口A南偏东15°方向9海里处,则船B与船C之间的距离为__________海里.
三、解答题
16.如图,某人为了测量小山顶上的塔顶离地面的高度,他在山下的点A处测得塔尖点D的仰角为,再沿方向前进到达山脚点B,测得塔尖点D的仰角为,求的高度(结果保留根号)
17.如图,星期天小明去钓鱼,鱼钩在离水面的的1.3米处,在距离鱼线1.2米处点的水下0.8米处有一条鱼发现了鱼饵,于是以0.2米/秒的速度向鱼饵游去,那么这条鱼至少几秒后才能到达鱼饵处?
18.台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点
C为一海港,且点
C与直线AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有
小时.
参考答案
1.D
2.C
3.C
4.A
5.B
6.B
7.B
8.D
9.C
10.C
11.
12.5m
13.
14.20
15.
16.
17.6.5
18.(1)海港C受台风影响.
理由:如图,过点C作CD⊥AB于D,
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
∴AC?BC=CD?AB
∴CD=240(km)
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C受到台风影响.
(2)当EC=250km,FC=250km时,正好影响C港口,
∵ED==70(km)
∴EF=140km
∵台风的速度为20km/h,
∴140÷20=7(小时)
即台风影响该海港持续的时间为7小时.
故答案为:7.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
