六年级数学上册《圆的周长》 课件 人教版(19张PPT)
文档属性
| 名称 | 六年级数学上册《圆的周长》 课件 人教版(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 22:40:09 | ||
图片预览




文档简介
(共19张PPT)
圆
的
周
长
围成一个平面图形所有边长的总和叫做这个图形的周长。
围成圆的曲线的长叫做圆的周长。
同学们,你们有办法解决吗?
圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。
分别需要多长的铁皮啊?
0
1
2
3
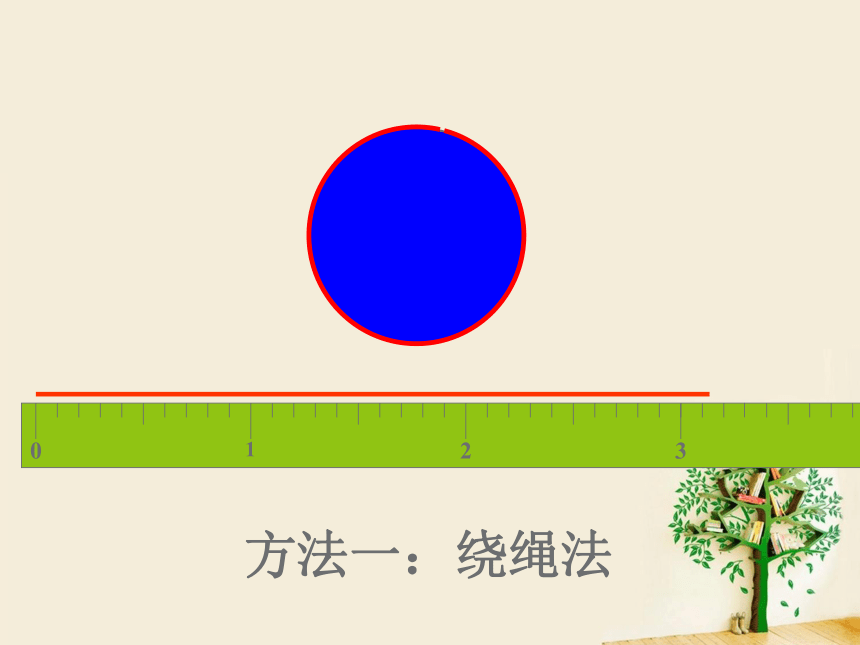
方法一:绕绳法
0
1
2
3
4
方法二:滚动法
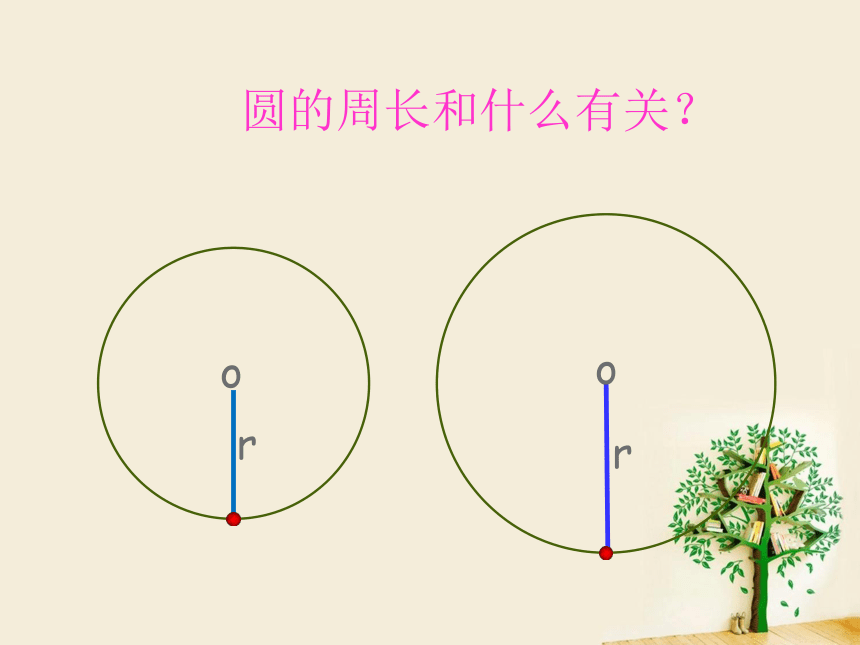
圆的周长和什么有关?
o
o
r
r
让我们来做一个实验,找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入下表中。看看你有什么发现。
物品名称
周长
(毫米)
直径
(毫米)
(保留两位小数)
一角硬币
手镯
五角硬币
一元硬币
7.5
6.3
22
2
2.4
7
2.2
6.9
3.14
3.15
3.14
3.13
物品名称
周长
(毫米)
直径
(毫米)
(保留两位小数)
一角硬币
手镯
五角硬币
一元硬币
7.5
6.3
22
2
2.4
7
2.2
6.9
3.14
3.15
3.14
3.13
你发现圆的周长和直径之间有什么关系?
一个圆的周长总是它的直径的3倍多一些。
其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母“π
(读pài)”表示。他是一个无限不循环小数,π=
3.1415926535……但在实际应用中一般只取它的近似值,即π≈3.14。
π>3.14
祖冲之
约1500年前,中国有一位伟大的数学家和天文学家祖冲之。他计算出圆周率应在3.1415926
和3.1415927
之间,成为世界上第一个把圆周率的值的计算精确到7
位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早一千年。
C
=
πd
C
=
2πr
圆的周长
=
直径×圆周率
d=
C
π
r
=
C
2π
圆的周长÷圆的直径=圆周率
C
÷
d
=
π
1.两个圆的周长相等,那么这两个圆的直径也相等。
(
)
√
2.π=3.14
(
)
×
二、选择填空。
1.车轮滚动一周,前进的距离是求车轮的(
)
A.半径
B.直径
C.周长
2.圆的周长是直径的(
)倍。
A.3.14
B.π
C.3
3.大圆的周长除以直径的商(
)小圆的周长
除以直径的商。
A.大于
B.小于
C.等于
C
B
C
一、判断。
求出下列各圆的周长
d=2厘米
r=2厘米
3.14×2
=6.28
(厘米)
2×3.14×2
=6.28×2
=12.56
(厘米)
这辆自行车后轮转一圈,大约可以走多远?(结果保留整米数。)
小明家离学校1km,骑车从家到学校,轮子大约转了多少圈?
2×3.14×33=207.24(cm)≈
2(m)
1000÷2
=500(圈)
1
km=1000
m
答:这辆自行车后轮转一圈,大约可以走2
m。小明从家到学校,
后轮转500圈。
例1
这辆自行车后轮轮胎的半径大约是33cm。
C=2πr
1、一个圆形喷水池的半径是5m,它的周长是多少米?
2×3.14×5
=3.14×10
=31.4(m)
答:它的周长是31.4米。
2、在一个圆形亭子里,小丽走完它的直径需用12步,每步长大约是55厘米,这个圆形亭子的周长大约是多少?
3.14×12×55=2072.4(厘米)
答:这个圆的周长大约是2072.4厘米。
山路曲折盘旋,
但毕竟朝着顶峰延伸。
圆
的
周
长
围成一个平面图形所有边长的总和叫做这个图形的周长。
围成圆的曲线的长叫做圆的周长。
同学们,你们有办法解决吗?
圆桌和菜板都有点开裂,需要在它们的边缘箍上一圈铁皮。
分别需要多长的铁皮啊?
0
1
2
3
方法一:绕绳法
0
1
2
3
4
方法二:滚动法
圆的周长和什么有关?
o
o
r
r
让我们来做一个实验,找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入下表中。看看你有什么发现。
物品名称
周长
(毫米)
直径
(毫米)
(保留两位小数)
一角硬币
手镯
五角硬币
一元硬币
7.5
6.3
22
2
2.4
7
2.2
6.9
3.14
3.15
3.14
3.13
物品名称
周长
(毫米)
直径
(毫米)
(保留两位小数)
一角硬币
手镯
五角硬币
一元硬币
7.5
6.3
22
2
2.4
7
2.2
6.9
3.14
3.15
3.14
3.13
你发现圆的周长和直径之间有什么关系?
一个圆的周长总是它的直径的3倍多一些。
其实,早就有人研究了周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母“π
(读pài)”表示。他是一个无限不循环小数,π=
3.1415926535……但在实际应用中一般只取它的近似值,即π≈3.14。
π>3.14
祖冲之
约1500年前,中国有一位伟大的数学家和天文学家祖冲之。他计算出圆周率应在3.1415926
和3.1415927
之间,成为世界上第一个把圆周率的值的计算精确到7
位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早一千年。
C
=
πd
C
=
2πr
圆的周长
=
直径×圆周率
d=
C
π
r
=
C
2π
圆的周长÷圆的直径=圆周率
C
÷
d
=
π
1.两个圆的周长相等,那么这两个圆的直径也相等。
(
)
√
2.π=3.14
(
)
×
二、选择填空。
1.车轮滚动一周,前进的距离是求车轮的(
)
A.半径
B.直径
C.周长
2.圆的周长是直径的(
)倍。
A.3.14
B.π
C.3
3.大圆的周长除以直径的商(
)小圆的周长
除以直径的商。
A.大于
B.小于
C.等于
C
B
C
一、判断。
求出下列各圆的周长
d=2厘米
r=2厘米
3.14×2
=6.28
(厘米)
2×3.14×2
=6.28×2
=12.56
(厘米)
这辆自行车后轮转一圈,大约可以走多远?(结果保留整米数。)
小明家离学校1km,骑车从家到学校,轮子大约转了多少圈?
2×3.14×33=207.24(cm)≈
2(m)
1000÷2
=500(圈)
1
km=1000
m
答:这辆自行车后轮转一圈,大约可以走2
m。小明从家到学校,
后轮转500圈。
例1
这辆自行车后轮轮胎的半径大约是33cm。
C=2πr
1、一个圆形喷水池的半径是5m,它的周长是多少米?
2×3.14×5
=3.14×10
=31.4(m)
答:它的周长是31.4米。
2、在一个圆形亭子里,小丽走完它的直径需用12步,每步长大约是55厘米,这个圆形亭子的周长大约是多少?
3.14×12×55=2072.4(厘米)
答:这个圆的周长大约是2072.4厘米。
山路曲折盘旋,
但毕竟朝着顶峰延伸。
