2020-2021学年湖南省张家界市永定区八年级(下)期中数学试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年湖南省张家界市永定区八年级(下)期中数学试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 612.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 07:46:13 | ||
图片预览


文档简介
2020-2021学年湖南省张家界市永定区八年级(下)期中数学试卷
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
2.在Rt△ABC中,M为斜边AB的中点,且BC=2,AB=5,则线段CM的长是( )
A.1
B.2
C.2.5
D.3
3.矩形具有而平行四边形不具有的性质是( )
A.对角线互相平分
B.对角线相等
C.对角线互相垂直
D.四边相等
4.下列各组数据中,不能作为直角三角形边长的是( )
A.3,5,7
B.6,8,10
C.5,12,13
D.1,2,
5.下列说法正确的是( )
①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部;
③三角形的一条中线把该三角形分成面积相等的两部分;
④三角形的三条高都在三角形内部.
A.①②
B.②③
C.③④
D.②④
6.如图所示,在平行四边形ABCD中,已知AC=3cm,若△ABC的周长为11cm,则平行四边形的周长为( )
A.6cm
B.12cm
C.16cm
D.11cm
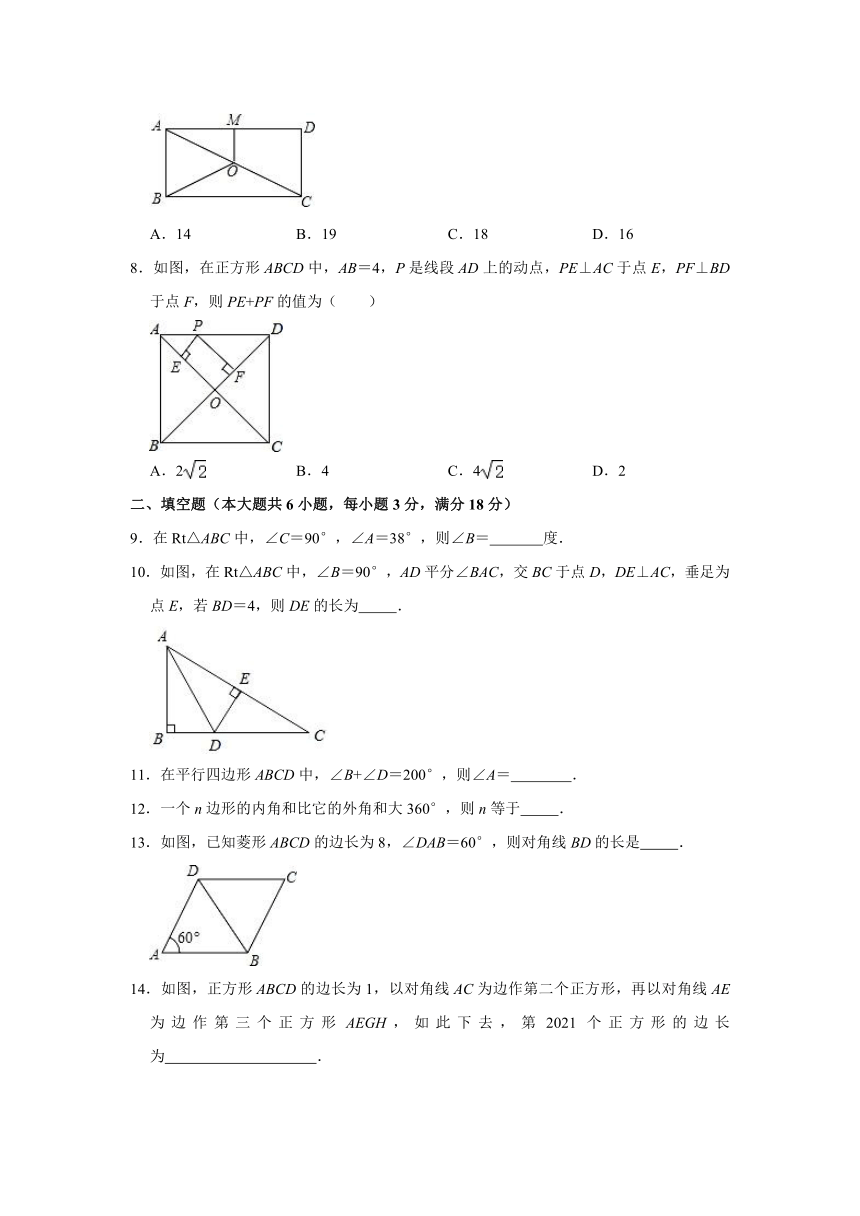
7.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长是( )
A.14
B.19
C.18
D.16
8.如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.2
B.4
C.4
D.2
二、填空题(本大题共6小题,每小题3分,满分18分)
9.在Rt△ABC中,∠C=90°,∠A=38°,则∠B=
度.
10.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=4,则DE的长为
.
11.在平行四边形ABCD中,∠B+∠D=200°,则∠A=
.
12.一个n边形的内角和比它的外角和大360°,则n等于
.
13.如图,已知菱形ABCD的边长为8,∠DAB=60°,则对角线BD的长是
.
14.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第2021个正方形的边长为
.
三、解答题(本大题共8个小题,共计58分)
15.如图,正方形ABCD中,点E,F分别在AD,CD上,且BE=AF,连接BE,AF.求证:AE=DF.
16.如图,已知,AE⊥BD于E点,CF⊥BD于F点,∠1=∠2,BE=DF,连接AB,CD.求证:四边形ABCD是平行四边形.
17.如图,在△ABC中,CD⊥AB于点D,AC=20,AD=16,CB=15.
(1)求DC,AB的长;
(2)求证:△ABC是直角三角形.
18.如图,木工师傅将一根长2.5米的梯子(AB),斜靠在与地面(OM)垂直的墙(ON)上,这时梯足B到墙底端O的距离是0.7米,如果梯子的顶端A沿墙下滑0.4米到点A′时,梯足将外移多少米?
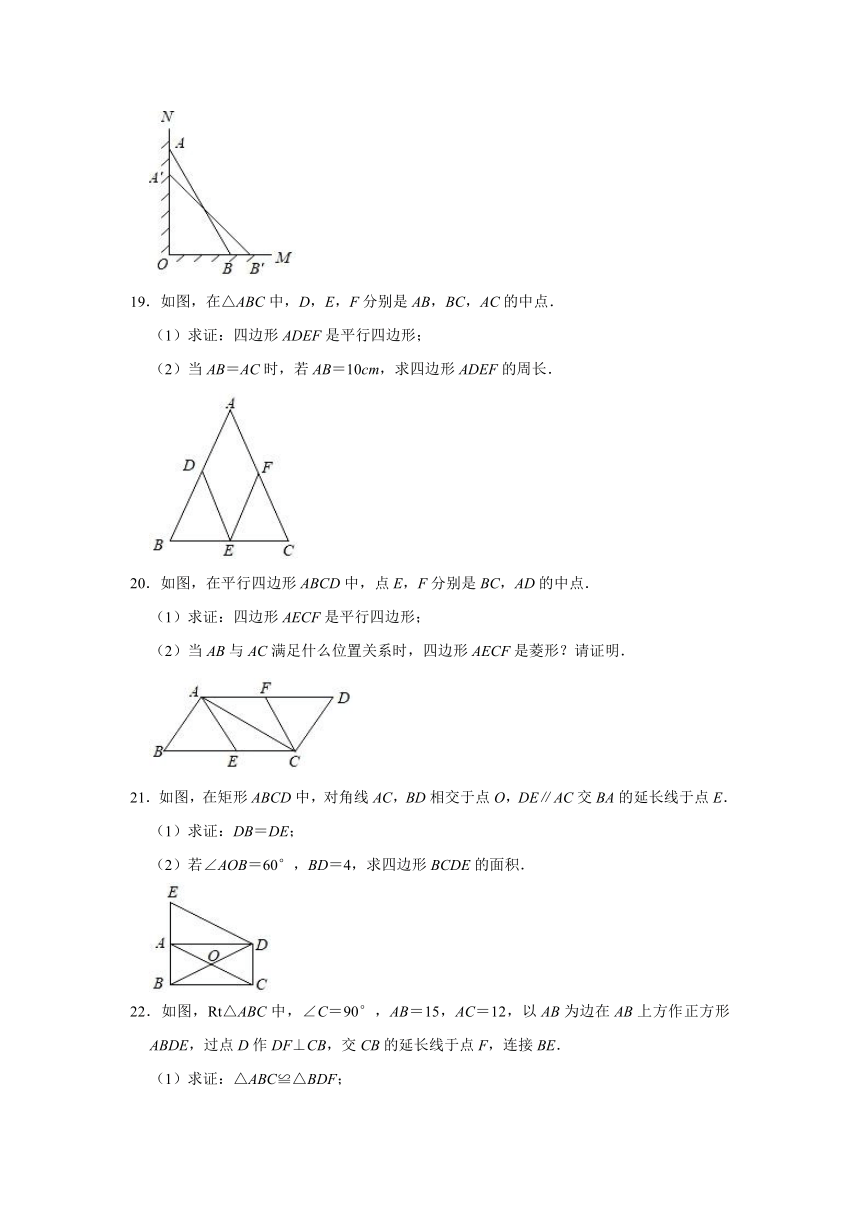
19.如图,在△ABC中,D,E,F分别是AB,BC,AC的中点.
(1)求证:四边形ADEF是平行四边形;
(2)当AB=AC时,若AB=10cm,求四边形ADEF的周长.
20.如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)当AB与AC满足什么位置关系时,四边形AECF是菱形?请证明.
21.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE∥AC交BA的延长线于点E.
(1)求证:DB=DE;
(2)若∠AOB=60°,BD=4,求四边形BCDE的面积.
22.如图,Rt△ABC中,∠C=90°,AB=15,AC=12,以AB为边在AB上方作正方形ABDE,过点D作DF⊥CB,交CB的延长线于点F,连接BE.
(1)求证:△ABC≌△BDF;
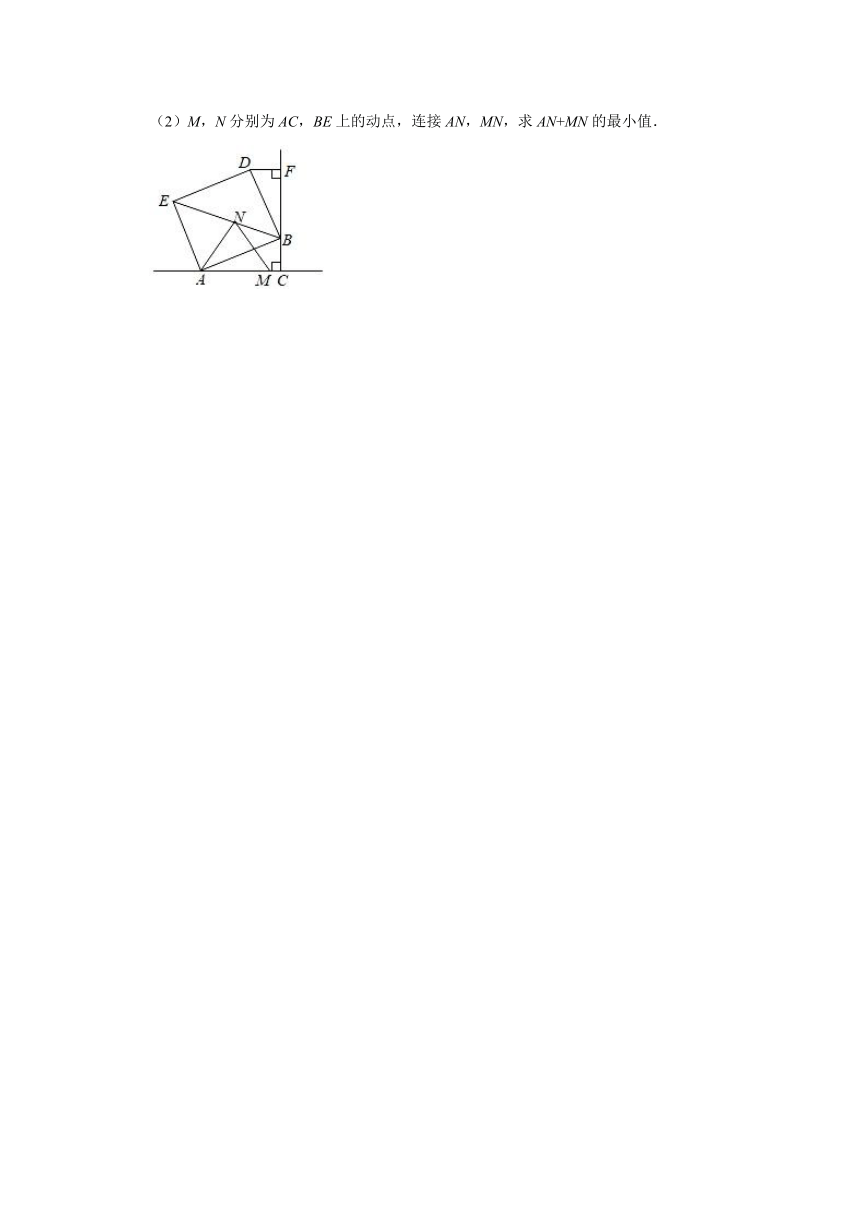
(2)M,N分别为AC,BE上的动点,连接AN,MN,求AN+MN的最小值.
参考答案
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形与中心对称图形的概念求解.
解:A、是轴对称图形,不是中心对称图形,故此选项错误;
B、是轴对称图形,不是中心对称图形,故此选项错误;
C、不是轴对称图形,是中心对称图形,故此选项错误;
D、既是轴对称图形,又是中心对称图形,故此选项正确;
故选:D.
2.在Rt△ABC中,M为斜边AB的中点,且BC=2,AB=5,则线段CM的长是( )
A.1
B.2
C.2.5
D.3
【分析】根据“在直角三角形中,斜边上的中线等于斜边的一半”解答.
解:在Rt△ABC中,M为斜边AB的中点,则CM是Rt△ABC斜边上的中线.
∵AB=5,
∴CM=AB=2.5.
故选:C.
3.矩形具有而平行四边形不具有的性质是( )
A.对角线互相平分
B.对角线相等
C.对角线互相垂直
D.四边相等
【分析】由矩形的性质和平行四边形的性质即可得出结论.
解:∵矩形的对角线互相平分且相等,平行四边形的对角线互相平分;
∴矩形具有而平行四边形不具有的性质是对角线相等;
故选:B.
4.下列各组数据中,不能作为直角三角形边长的是( )
A.3,5,7
B.6,8,10
C.5,12,13
D.1,2,
【分析】根据勾股定理的逆定理,可以判断各个选项中的三条线段是否能构成直角三角形,从而可以解答本题.
解:32+52≠72,故选项A符合题意;
62+82=102,故选项B不符合题意;
52+122=132,故选项C不符合题意;
12+()2=22,故选项D不符合题意;
故选:A.
5.下列说法正确的是( )
①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部;
③三角形的一条中线把该三角形分成面积相等的两部分;
④三角形的三条高都在三角形内部.
A.①②
B.②③
C.③④
D.②④
【分析】根据三角形的角平分线的定义与性质判断①与②;根据三角形的高的定义及性质判断④;根据三角形的中线的定义及性质判断③即可.
解:①三角形的角平分线是线段,故①说法错误;
②三角形的三条角平分线都在三角形内部,故②说法正确;
③三角形的一条中线把该三角形分成面积相等的两部分,故③说法正确;
④锐角三角形的三条高都在三角形内部;直角三角形有两条高与直角边重合,另一条高在三角形内部;钝角三角形有两条高在三角形外部,一条高在三角形内部.故④说法错误.
故正确的有②③.
故选:B.
6.如图所示,在平行四边形ABCD中,已知AC=3cm,若△ABC的周长为11cm,则平行四边形的周长为( )
A.6cm
B.12cm
C.16cm
D.11cm
【分析】由平行四边形的对边相等直接可求解.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AC=3cm,△ABC的周长为11cm,
∴AB+BC=8(cm),
∴平行四边形的周长=2×8=16(cm),
故选:C.
7.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长是( )
A.14
B.19
C.18
D.16
【分析】根据矩形的性质,直角三角形斜边中线性质,三角形中位线性质求出BO、OM、AM即可解决问题.
解:∵四边形ABCD是矩形,
∴AD=BC=8,AB=CD=6,∠ABC=90°,
∴AC==10,
∵AO=OC,
∴BO=AC=5,
∵AO=OC,AM=MD=4,
∴OM=CD=3,
∴四边形ABOM的周长为AB+OB+OM+AM=6+5+3+4=18.
故选:C.
8.如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.2
B.4
C.4
D.2
【分析】根据正方形的对角线互相垂直可得OA⊥OD,对角线平分一组对角可得∠OAD=45°,然后求出四边形OEPF为矩形,△APE是等腰直角三角形,再根据矩形的对边相等可得PF=OE,根据等腰直角三角形的性质可得PE=BE,从而得到PE+PF=OA,然后根据正方形的性质解答即可.
解:在正方形ABCD中,OA⊥OD,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△APE是等腰直角三角形,
∴PF=OE,PE=BE,
∴PE+PF=BE+OE=OA,
∵AB=BC=4,
∴OA=AC==2,
∴PE+PF=2,
故选:A.
二、填空题(本大题共6小题,每小题3分,满分18分)
9.在Rt△ABC中,∠C=90°,∠A=38°,则∠B= 52 度.
【分析】根据直角三角形的性质即可得到结论.
解:在Rt△ABC中,∠C=90°,∠A=38°,
则∠B=90°﹣38°=52°,
故答案为:52.
10.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=4,则DE的长为 4 .
【分析】根据角平分线的性质解答即可.
解:∵AD平分∠BAC,∠B=90°,DE⊥AC,
∴DE=BD=4,
故答案为:4.
11.在平行四边形ABCD中,∠B+∠D=200°,则∠A= 80° .
【分析】利用平行四边形的对角相等、邻角互补可求得答案.
解:
∵四边形ABCD为平行四边形,
∴∠B=∠D,∠A+∠B=180°,
∵∠B+∠D=200°,
∴∠B=∠D=100°,
∴∠A=180°﹣∠B=180°﹣100°=80°,
故答案为:80°.
12.一个n边形的内角和比它的外角和大360°,则n等于 6 .
【分析】根据n边形的内角和为(n﹣2)?180°,外角和等于360°列出方程求解即可.
解:根据题意得:
(n﹣2)?180°﹣360°=360°,
解得n=6.
故答案为:6.
13.如图,已知菱形ABCD的边长为8,∠DAB=60°,则对角线BD的长是 8 .
【分析】由菱形的性质得AB=AD=8,再证△ABD是等边三角形,得BD=AB=8即可.
解:∵菱形ABCD的边长为8,
∴AB=AD=8,
∵∠DAB=60°,
∴△ABD是等边三角形,
∴BD=AB=8,
故答案为:8.
14.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第2021个正方形的边长为 ()2020 .
【分析】求出AC、AE、HE的长度,然后猜测命题中隐含的数学规律,即可解决问题.
解:∵四边形ABCD为正方形,
∴AB=BC=1,∠B=90°,
∴AC2=12+12,AC=;
同理可求:AE=()2,HE=()3…,
∴第n个正方形的边长an=()n﹣1,
∴第2021个正方形的边长为()2020,
故答案为:()2020.
三、解答题(本大题共8个小题,共计58分)
15.如图,正方形ABCD中,点E,F分别在AD,CD上,且BE=AF,连接BE,AF.求证:AE=DF.
【分析】根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°,然后利用“HL”证明Rt△BAE≌Rt△ADF,根据全等三角形对应边相等证明即可.
【解答】证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD,
又∵BE=AF,
在Rt△BAE和Rt△ADF中,
,
∴Rt△BAE≌Rt△ADF(HL),
∴AE=DF.
16.如图,已知,AE⊥BD于E点,CF⊥BD于F点,∠1=∠2,BE=DF,连接AB,CD.求证:四边形ABCD是平行四边形.
【分析】由垂直的定义得到∠AED=∠BFC=90°,得到BF=DE根据全等三角形的性质得到AD=BC,根据平行线的判定定理得到AD∥BC,于是得到结论.
【解答】证明:∵AE⊥BD于E点,CF⊥BD于F点,
∴∠AED=∠BFC=90°,
∵BE=DF,
∴BE+EF=DF+EF,
即:BF=DE
又∵∠1=∠2,
∴△ADE≌△CBF(ASA),
∴AD=BC,
又∵∠1=∠2,
∴AD∥BC,
∴四边形ABCD是平行四边形.
17.如图,在△ABC中,CD⊥AB于点D,AC=20,AD=16,CB=15.
(1)求DC,AB的长;
(2)求证:△ABC是直角三角形.
【分析】(1)根据勾股定理,可以求得CD的长,再根据BC的长,利用勾股定理可以得到BD的长,然后即可求得AB的长;
(2)根据题目中的数据和(1)中得到的AB的长,利用勾股定理的逆定理,即可判断△ABC的形状.
解:(1)∵CD⊥AB,AC=20,AD=16,
∴CD===12,
∵CB=15,CD⊥AB,
∴BD===9,
∴AB=AD+BD=16+9=25,
由上可得,DC的长是12,AB的长是25;
(2)证明:∵AC=20,BC=15,AB=25,
∴AC2+BC2=202+152=400+225=625=252=AB2,
∴△ABC是直角三角形.
18.如图,木工师傅将一根长2.5米的梯子(AB),斜靠在与地面(OM)垂直的墙(ON)上,这时梯足B到墙底端O的距离是0.7米,如果梯子的顶端A沿墙下滑0.4米到点A′时,梯足将外移多少米?
【分析】在直角△ABO中,已知AB,BO可以求AO,在△A′OB′中,再利用勾股定理计算出B′O的长,进而可得BB′的长.
解:在直角△ABO中,AB为斜边,已知AB=2.5米,BO=0.7米,
则根据勾股定理求得AO===2.4(米),
∵A点下移0.4米,
∴A′O=2米,
在Rt△A′OB′中,已知A′B′=2.5米,A′O=2米,
则根据勾股定理B′O==1.5(米),
∴BB′=OB′﹣BO=1.5﹣0.7=0.8(米),
所以梯子向外平移0.8米.
19.如图,在△ABC中,D,E,F分别是AB,BC,AC的中点.
(1)求证:四边形ADEF是平行四边形;
(2)当AB=AC时,若AB=10cm,求四边形ADEF的周长.
【分析】(1)根据三角形的中位线的性质得到DE∥AF,EF∥AD,根据平行四边形的判定定理即可得到结论;
(2)根据菱形的判定得出四边形ADEF是菱形,于是得到结论.
【解答】(1)证明:∵D,E,F分别是AB,BC,AC的中点,
∴DE,EF分别是△ABC
的中位线,
∴DE∥AC,EF∥AB,
∴DE∥AF,EF∥AD,
∴四边形ADEF是平行四边形;
(2)解:∵D是AB的中点,F是AC的中点,AB=10cm,AB=AC,
∴AD=AF=AB=5(cm),
∵四边形ADEF是平行四边形,
∴四边形ADEF是菱形,
∴四边形ADEF的周长为4AD=4×5=20(cm).
20.如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)当AB与AC满足什么位置关系时,四边形AECF是菱形?请证明.
【分析】(1)由平行四边形的性质得AD=BC,AD∥BC,再由已知条件得AF=EC,AF∥EC,即可得出结论;
(2)由直角三角形斜边上的中线性质得AE=BC=CE,再由菱形的判定即可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点E,F分别是BC,AD的中点.
∴AF=DF=AD,BE=CE=BC,
∴AF=CE且AF∥EC,
∴四边形AECF是平行四边形.
(2)解:当AB⊥AC时,四边形
AECF是菱形,证明如下:
由(1)得:四边形AECF是平行四边形,
∵AB⊥AC,
∴∠BAC=90°,
∵点E是BC的中点,
∴AE=BC=CE,
∴平行四边形AECF是菱形.
21.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE∥AC交BA的延长线于点E.
(1)求证:DB=DE;
(2)若∠AOB=60°,BD=4,求四边形BCDE的面积.
【分析】(1)由矩形的性质可得AC=BD,AB∥CD,可证四边形ACDE是平行四边形,可得DE=AC=BD;
(2)由矩形的性质可得OA=OB=2,可证△ABO是等边三角形,可得AB=2,由勾股定理可求AD,由面积和差关系可求解.
【解答】证明:(1)∵四边形ABCD是矩形,
∴AB=CD,AC=BD,AB∥CD,
又∵DE∥AC,
∴四边形ACDE是平行四边形,
∴DE=AC,CD=AE,
∴DE=BD;
(2)∵四边形ABCD是矩形,
∴AC=BD=4,AO=CO,BO=DO,
∴AO=BO=2,
又∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=2=CD=AE,
∴AD===2,
∴四边形BCDE的面积=×2×2+2×2=6.
22.如图,Rt△ABC中,∠C=90°,AB=15,AC=12,以AB为边在AB上方作正方形ABDE,过点D作DF⊥CB,交CB的延长线于点F,连接BE.
(1)求证:△ABC≌△BDF;
(2)M,N分别为AC,BE上的动点,连接AN,MN,求AN+MN的最小值.
【分析】(1)根据正方形的性质得出BD=AB,∠DBA=90°,进而得出∠DBF=∠CAB,因为∠C=∠DFB=90°.根据AAS即可证得结论;
(2)根据正方形的性质AN=DN,如使得AN+MN最小,只需D、N、M在一条直线上,根据垂线段最短,作DM1⊥AC,交BE于点N1,垂足为M1,则AN+MN的最小值等于DM1=FC=21.
【解答】(1)证明:在Rt△ABC中,∠C=90°,DF⊥CB,
∴∠C=∠DFB=90°.
∵四边形ABDE是正方形,
∴BD=AB,∠DBA=90°,
∵∠DBF+∠ABC=90°,∠CAB+∠ABC=90°,
∴∠DBF=∠CAB,
在△BDF与△ABC中,
,
∴△BDF≌△ABC(AAS);
(2)解:∵AB=15,AC=12,
∴BC==9,
∵△ABC≌△BDF,
∴DF=BC=9,BF=AC=12,
∴FC=BF+BC=9+12=21.
如图,连接DN,
∵顶点A与顶点D关于BE对称,
∴AN=DN.
如使得AN+MN最小,只需D、N、M在一条直线上,
由于点M、N分别是AC和BE上的动点,
作DM1⊥AC,交BE于点N1,垂足为M1,
∵DF∥AC,
∴AN+MN的最小值等于DM1=FC=21.
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
2.在Rt△ABC中,M为斜边AB的中点,且BC=2,AB=5,则线段CM的长是( )
A.1
B.2
C.2.5
D.3
3.矩形具有而平行四边形不具有的性质是( )
A.对角线互相平分
B.对角线相等
C.对角线互相垂直
D.四边相等
4.下列各组数据中,不能作为直角三角形边长的是( )
A.3,5,7
B.6,8,10
C.5,12,13
D.1,2,
5.下列说法正确的是( )
①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部;
③三角形的一条中线把该三角形分成面积相等的两部分;
④三角形的三条高都在三角形内部.
A.①②
B.②③
C.③④
D.②④
6.如图所示,在平行四边形ABCD中,已知AC=3cm,若△ABC的周长为11cm,则平行四边形的周长为( )
A.6cm
B.12cm
C.16cm
D.11cm
7.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长是( )
A.14
B.19
C.18
D.16
8.如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.2
B.4
C.4
D.2
二、填空题(本大题共6小题,每小题3分,满分18分)
9.在Rt△ABC中,∠C=90°,∠A=38°,则∠B=
度.
10.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=4,则DE的长为
.
11.在平行四边形ABCD中,∠B+∠D=200°,则∠A=
.
12.一个n边形的内角和比它的外角和大360°,则n等于
.
13.如图,已知菱形ABCD的边长为8,∠DAB=60°,则对角线BD的长是
.
14.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第2021个正方形的边长为
.
三、解答题(本大题共8个小题,共计58分)
15.如图,正方形ABCD中,点E,F分别在AD,CD上,且BE=AF,连接BE,AF.求证:AE=DF.
16.如图,已知,AE⊥BD于E点,CF⊥BD于F点,∠1=∠2,BE=DF,连接AB,CD.求证:四边形ABCD是平行四边形.
17.如图,在△ABC中,CD⊥AB于点D,AC=20,AD=16,CB=15.
(1)求DC,AB的长;
(2)求证:△ABC是直角三角形.
18.如图,木工师傅将一根长2.5米的梯子(AB),斜靠在与地面(OM)垂直的墙(ON)上,这时梯足B到墙底端O的距离是0.7米,如果梯子的顶端A沿墙下滑0.4米到点A′时,梯足将外移多少米?
19.如图,在△ABC中,D,E,F分别是AB,BC,AC的中点.
(1)求证:四边形ADEF是平行四边形;
(2)当AB=AC时,若AB=10cm,求四边形ADEF的周长.
20.如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)当AB与AC满足什么位置关系时,四边形AECF是菱形?请证明.
21.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE∥AC交BA的延长线于点E.
(1)求证:DB=DE;
(2)若∠AOB=60°,BD=4,求四边形BCDE的面积.
22.如图,Rt△ABC中,∠C=90°,AB=15,AC=12,以AB为边在AB上方作正方形ABDE,过点D作DF⊥CB,交CB的延长线于点F,连接BE.
(1)求证:△ABC≌△BDF;
(2)M,N分别为AC,BE上的动点,连接AN,MN,求AN+MN的最小值.
参考答案
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形与中心对称图形的概念求解.
解:A、是轴对称图形,不是中心对称图形,故此选项错误;
B、是轴对称图形,不是中心对称图形,故此选项错误;
C、不是轴对称图形,是中心对称图形,故此选项错误;
D、既是轴对称图形,又是中心对称图形,故此选项正确;
故选:D.
2.在Rt△ABC中,M为斜边AB的中点,且BC=2,AB=5,则线段CM的长是( )
A.1
B.2
C.2.5
D.3
【分析】根据“在直角三角形中,斜边上的中线等于斜边的一半”解答.
解:在Rt△ABC中,M为斜边AB的中点,则CM是Rt△ABC斜边上的中线.
∵AB=5,
∴CM=AB=2.5.
故选:C.
3.矩形具有而平行四边形不具有的性质是( )
A.对角线互相平分
B.对角线相等
C.对角线互相垂直
D.四边相等
【分析】由矩形的性质和平行四边形的性质即可得出结论.
解:∵矩形的对角线互相平分且相等,平行四边形的对角线互相平分;
∴矩形具有而平行四边形不具有的性质是对角线相等;
故选:B.
4.下列各组数据中,不能作为直角三角形边长的是( )
A.3,5,7
B.6,8,10
C.5,12,13
D.1,2,
【分析】根据勾股定理的逆定理,可以判断各个选项中的三条线段是否能构成直角三角形,从而可以解答本题.
解:32+52≠72,故选项A符合题意;
62+82=102,故选项B不符合题意;
52+122=132,故选项C不符合题意;
12+()2=22,故选项D不符合题意;
故选:A.
5.下列说法正确的是( )
①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部;
③三角形的一条中线把该三角形分成面积相等的两部分;
④三角形的三条高都在三角形内部.
A.①②
B.②③
C.③④
D.②④
【分析】根据三角形的角平分线的定义与性质判断①与②;根据三角形的高的定义及性质判断④;根据三角形的中线的定义及性质判断③即可.
解:①三角形的角平分线是线段,故①说法错误;
②三角形的三条角平分线都在三角形内部,故②说法正确;
③三角形的一条中线把该三角形分成面积相等的两部分,故③说法正确;
④锐角三角形的三条高都在三角形内部;直角三角形有两条高与直角边重合,另一条高在三角形内部;钝角三角形有两条高在三角形外部,一条高在三角形内部.故④说法错误.
故正确的有②③.
故选:B.
6.如图所示,在平行四边形ABCD中,已知AC=3cm,若△ABC的周长为11cm,则平行四边形的周长为( )
A.6cm
B.12cm
C.16cm
D.11cm
【分析】由平行四边形的对边相等直接可求解.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AC=3cm,△ABC的周长为11cm,
∴AB+BC=8(cm),
∴平行四边形的周长=2×8=16(cm),
故选:C.
7.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长是( )
A.14
B.19
C.18
D.16
【分析】根据矩形的性质,直角三角形斜边中线性质,三角形中位线性质求出BO、OM、AM即可解决问题.
解:∵四边形ABCD是矩形,
∴AD=BC=8,AB=CD=6,∠ABC=90°,
∴AC==10,
∵AO=OC,
∴BO=AC=5,
∵AO=OC,AM=MD=4,
∴OM=CD=3,
∴四边形ABOM的周长为AB+OB+OM+AM=6+5+3+4=18.
故选:C.
8.如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.2
B.4
C.4
D.2
【分析】根据正方形的对角线互相垂直可得OA⊥OD,对角线平分一组对角可得∠OAD=45°,然后求出四边形OEPF为矩形,△APE是等腰直角三角形,再根据矩形的对边相等可得PF=OE,根据等腰直角三角形的性质可得PE=BE,从而得到PE+PF=OA,然后根据正方形的性质解答即可.
解:在正方形ABCD中,OA⊥OD,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△APE是等腰直角三角形,
∴PF=OE,PE=BE,
∴PE+PF=BE+OE=OA,
∵AB=BC=4,
∴OA=AC==2,
∴PE+PF=2,
故选:A.
二、填空题(本大题共6小题,每小题3分,满分18分)
9.在Rt△ABC中,∠C=90°,∠A=38°,则∠B= 52 度.
【分析】根据直角三角形的性质即可得到结论.
解:在Rt△ABC中,∠C=90°,∠A=38°,
则∠B=90°﹣38°=52°,
故答案为:52.
10.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=4,则DE的长为 4 .
【分析】根据角平分线的性质解答即可.
解:∵AD平分∠BAC,∠B=90°,DE⊥AC,
∴DE=BD=4,
故答案为:4.
11.在平行四边形ABCD中,∠B+∠D=200°,则∠A= 80° .
【分析】利用平行四边形的对角相等、邻角互补可求得答案.
解:
∵四边形ABCD为平行四边形,
∴∠B=∠D,∠A+∠B=180°,
∵∠B+∠D=200°,
∴∠B=∠D=100°,
∴∠A=180°﹣∠B=180°﹣100°=80°,
故答案为:80°.
12.一个n边形的内角和比它的外角和大360°,则n等于 6 .
【分析】根据n边形的内角和为(n﹣2)?180°,外角和等于360°列出方程求解即可.
解:根据题意得:
(n﹣2)?180°﹣360°=360°,
解得n=6.
故答案为:6.
13.如图,已知菱形ABCD的边长为8,∠DAB=60°,则对角线BD的长是 8 .
【分析】由菱形的性质得AB=AD=8,再证△ABD是等边三角形,得BD=AB=8即可.
解:∵菱形ABCD的边长为8,
∴AB=AD=8,
∵∠DAB=60°,
∴△ABD是等边三角形,
∴BD=AB=8,
故答案为:8.
14.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第2021个正方形的边长为 ()2020 .
【分析】求出AC、AE、HE的长度,然后猜测命题中隐含的数学规律,即可解决问题.
解:∵四边形ABCD为正方形,
∴AB=BC=1,∠B=90°,
∴AC2=12+12,AC=;
同理可求:AE=()2,HE=()3…,
∴第n个正方形的边长an=()n﹣1,
∴第2021个正方形的边长为()2020,
故答案为:()2020.
三、解答题(本大题共8个小题,共计58分)
15.如图,正方形ABCD中,点E,F分别在AD,CD上,且BE=AF,连接BE,AF.求证:AE=DF.
【分析】根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°,然后利用“HL”证明Rt△BAE≌Rt△ADF,根据全等三角形对应边相等证明即可.
【解答】证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD,
又∵BE=AF,
在Rt△BAE和Rt△ADF中,
,
∴Rt△BAE≌Rt△ADF(HL),
∴AE=DF.
16.如图,已知,AE⊥BD于E点,CF⊥BD于F点,∠1=∠2,BE=DF,连接AB,CD.求证:四边形ABCD是平行四边形.
【分析】由垂直的定义得到∠AED=∠BFC=90°,得到BF=DE根据全等三角形的性质得到AD=BC,根据平行线的判定定理得到AD∥BC,于是得到结论.
【解答】证明:∵AE⊥BD于E点,CF⊥BD于F点,
∴∠AED=∠BFC=90°,
∵BE=DF,
∴BE+EF=DF+EF,
即:BF=DE
又∵∠1=∠2,
∴△ADE≌△CBF(ASA),
∴AD=BC,
又∵∠1=∠2,
∴AD∥BC,
∴四边形ABCD是平行四边形.
17.如图,在△ABC中,CD⊥AB于点D,AC=20,AD=16,CB=15.
(1)求DC,AB的长;
(2)求证:△ABC是直角三角形.
【分析】(1)根据勾股定理,可以求得CD的长,再根据BC的长,利用勾股定理可以得到BD的长,然后即可求得AB的长;
(2)根据题目中的数据和(1)中得到的AB的长,利用勾股定理的逆定理,即可判断△ABC的形状.
解:(1)∵CD⊥AB,AC=20,AD=16,
∴CD===12,
∵CB=15,CD⊥AB,
∴BD===9,
∴AB=AD+BD=16+9=25,
由上可得,DC的长是12,AB的长是25;
(2)证明:∵AC=20,BC=15,AB=25,
∴AC2+BC2=202+152=400+225=625=252=AB2,
∴△ABC是直角三角形.
18.如图,木工师傅将一根长2.5米的梯子(AB),斜靠在与地面(OM)垂直的墙(ON)上,这时梯足B到墙底端O的距离是0.7米,如果梯子的顶端A沿墙下滑0.4米到点A′时,梯足将外移多少米?
【分析】在直角△ABO中,已知AB,BO可以求AO,在△A′OB′中,再利用勾股定理计算出B′O的长,进而可得BB′的长.
解:在直角△ABO中,AB为斜边,已知AB=2.5米,BO=0.7米,
则根据勾股定理求得AO===2.4(米),
∵A点下移0.4米,
∴A′O=2米,
在Rt△A′OB′中,已知A′B′=2.5米,A′O=2米,
则根据勾股定理B′O==1.5(米),
∴BB′=OB′﹣BO=1.5﹣0.7=0.8(米),
所以梯子向外平移0.8米.
19.如图,在△ABC中,D,E,F分别是AB,BC,AC的中点.
(1)求证:四边形ADEF是平行四边形;
(2)当AB=AC时,若AB=10cm,求四边形ADEF的周长.
【分析】(1)根据三角形的中位线的性质得到DE∥AF,EF∥AD,根据平行四边形的判定定理即可得到结论;
(2)根据菱形的判定得出四边形ADEF是菱形,于是得到结论.
【解答】(1)证明:∵D,E,F分别是AB,BC,AC的中点,
∴DE,EF分别是△ABC
的中位线,
∴DE∥AC,EF∥AB,
∴DE∥AF,EF∥AD,
∴四边形ADEF是平行四边形;
(2)解:∵D是AB的中点,F是AC的中点,AB=10cm,AB=AC,
∴AD=AF=AB=5(cm),
∵四边形ADEF是平行四边形,
∴四边形ADEF是菱形,
∴四边形ADEF的周长为4AD=4×5=20(cm).
20.如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)当AB与AC满足什么位置关系时,四边形AECF是菱形?请证明.
【分析】(1)由平行四边形的性质得AD=BC,AD∥BC,再由已知条件得AF=EC,AF∥EC,即可得出结论;
(2)由直角三角形斜边上的中线性质得AE=BC=CE,再由菱形的判定即可得出结论.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点E,F分别是BC,AD的中点.
∴AF=DF=AD,BE=CE=BC,
∴AF=CE且AF∥EC,
∴四边形AECF是平行四边形.
(2)解:当AB⊥AC时,四边形
AECF是菱形,证明如下:
由(1)得:四边形AECF是平行四边形,
∵AB⊥AC,
∴∠BAC=90°,
∵点E是BC的中点,
∴AE=BC=CE,
∴平行四边形AECF是菱形.
21.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE∥AC交BA的延长线于点E.
(1)求证:DB=DE;
(2)若∠AOB=60°,BD=4,求四边形BCDE的面积.
【分析】(1)由矩形的性质可得AC=BD,AB∥CD,可证四边形ACDE是平行四边形,可得DE=AC=BD;
(2)由矩形的性质可得OA=OB=2,可证△ABO是等边三角形,可得AB=2,由勾股定理可求AD,由面积和差关系可求解.
【解答】证明:(1)∵四边形ABCD是矩形,
∴AB=CD,AC=BD,AB∥CD,
又∵DE∥AC,
∴四边形ACDE是平行四边形,
∴DE=AC,CD=AE,
∴DE=BD;
(2)∵四边形ABCD是矩形,
∴AC=BD=4,AO=CO,BO=DO,
∴AO=BO=2,
又∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=2=CD=AE,
∴AD===2,
∴四边形BCDE的面积=×2×2+2×2=6.
22.如图,Rt△ABC中,∠C=90°,AB=15,AC=12,以AB为边在AB上方作正方形ABDE,过点D作DF⊥CB,交CB的延长线于点F,连接BE.
(1)求证:△ABC≌△BDF;
(2)M,N分别为AC,BE上的动点,连接AN,MN,求AN+MN的最小值.
【分析】(1)根据正方形的性质得出BD=AB,∠DBA=90°,进而得出∠DBF=∠CAB,因为∠C=∠DFB=90°.根据AAS即可证得结论;
(2)根据正方形的性质AN=DN,如使得AN+MN最小,只需D、N、M在一条直线上,根据垂线段最短,作DM1⊥AC,交BE于点N1,垂足为M1,则AN+MN的最小值等于DM1=FC=21.
【解答】(1)证明:在Rt△ABC中,∠C=90°,DF⊥CB,
∴∠C=∠DFB=90°.
∵四边形ABDE是正方形,
∴BD=AB,∠DBA=90°,
∵∠DBF+∠ABC=90°,∠CAB+∠ABC=90°,
∴∠DBF=∠CAB,
在△BDF与△ABC中,
,
∴△BDF≌△ABC(AAS);
(2)解:∵AB=15,AC=12,
∴BC==9,
∵△ABC≌△BDF,
∴DF=BC=9,BF=AC=12,
∴FC=BF+BC=9+12=21.
如图,连接DN,
∵顶点A与顶点D关于BE对称,
∴AN=DN.
如使得AN+MN最小,只需D、N、M在一条直线上,
由于点M、N分别是AC和BE上的动点,
作DM1⊥AC,交BE于点N1,垂足为M1,
∵DF∥AC,
∴AN+MN的最小值等于DM1=FC=21.
同课章节目录
