第五章 分式与分式方程 专题复习(含解析)
文档属性
| 名称 | 第五章 分式与分式方程 专题复习(含解析) |

|
|
| 格式 | doc | ||
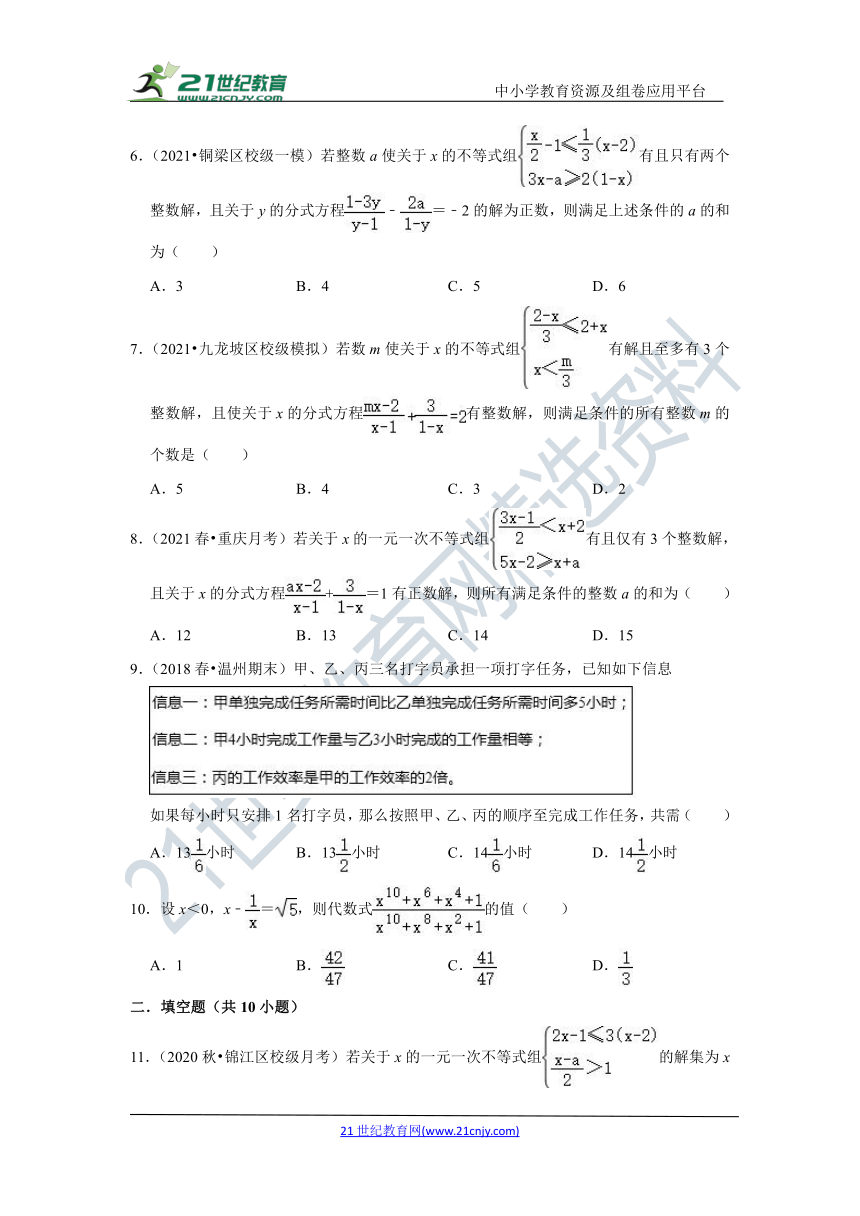
| 文件大小 | 629.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大新版数学专题复习《分式与分式方程》
一.选择题(共10小题)
1.(2021?十堰)某工厂现在平均每天比原计划多生产50台机器,现在生产400台机器所需时间比原计划生产450台机器所需时间少1天,设现在平均每天生产x台机器,则下列方程正确的是( )
A.﹣=1
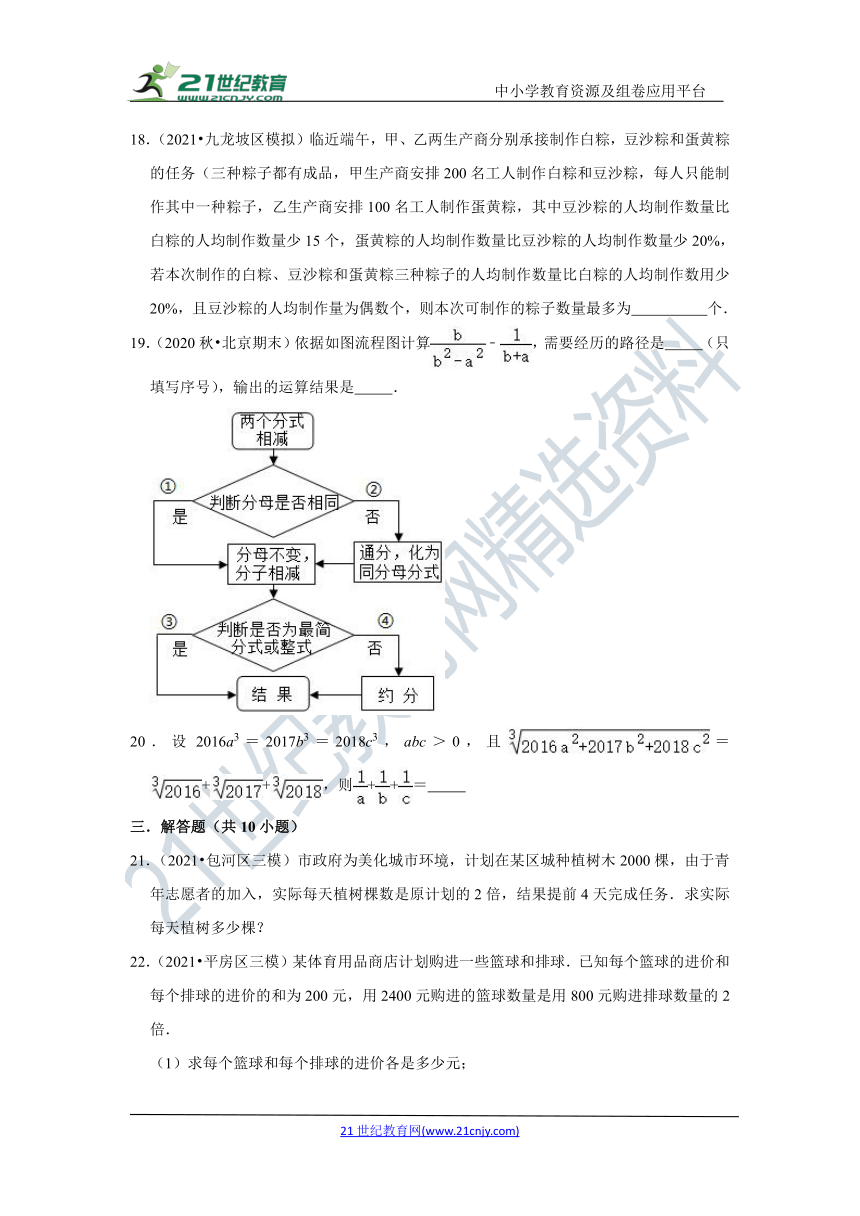
B.﹣=1
C.﹣=50
D.﹣=50
2.(2021?嘉兴)为迎接建党一百周年,某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威,其中缤纷棒共花费30元,荧光棒共花费40元,缤纷棒比荧光棒少20根,缤纷棒单价是荧光棒的1.5倍.若设荧光棒的单价为x元,根据题意可列方程为( )
A.﹣=20
B.﹣=20
C.﹣=20
D.﹣=20
3.(2021?重庆)若关于x的一元一次不等式组的解集为x≥6,且关于y的分式方程+=2的解是正整数,则所有满足条件的整数a的值之和是( )
A.5
B.8
C.12
D.15
4.(2021春?沙坪坝区校级月考)已知关于x的不等式组有解,且关于y的分式方程=4﹣有正整数解,则所有满足条件的整数a的值的个数为( )
A.2
B.3
C.4
D.5
5.(2021春?茅箭区月考)某施工队计划修建一个长为600米的隧道,第一周按原计划的速度修建,一周后以原来速度的1.5倍修建,结果比原计划提前一周完成任务,若设原计划一周修建隧道x米,则可列方程为( )
A.=+2
B.=﹣2
C.=+1
D.=﹣1
6.(2021?铜梁区校级一模)若整数a使关于x的不等式组有且只有两个整数解,且关于y的分式方程﹣=﹣2的解为正数,则满足上述条件的a的和为( )
A.3
B.4
C.5
D.6
7.(2021?九龙坡区校级模拟)若数m使关于x的不等式组有解且至多有3个整数解,且使关于x的分式方程有整数解,则满足条件的所有整数m的个数是( )
A.5
B.4
C.3
D.2
8.(2021春?重庆月考)若关于x的一元一次不等式组有且仅有3个整数解,且关于x的分式方程+=1有正数解,则所有满足条件的整数a的和为( )
A.12
B.13
C.14
D.15
9.(2018春?温州期末)甲、乙、丙三名打字员承担一项打字任务,已知如下信息
如果每小时只安排1名打字员,那么按照甲、乙、丙的顺序至完成工作任务,共需( )
A.13小时
B.13小时
C.14小时
D.14小时
10.设x<0,x﹣=,则代数式的值( )
A.1
B.
C.
D.
二.填空题(共10小题)
11.(2020秋?锦江区校级月考)若关于x的一元一次不等式组的解集为x≥5,且关于y的分式方程+=﹣1有非负整数解,则符合条件的所有整数a的和为
.
12.(2020秋?沙坪坝区校级月考)中秋、国庆“双节”前,某酒店推出甲,乙两种包装的月饼,其中甲种包装有五仁饼3个,莲蓉饼3个,豆沙饼2个,乙种包装有五仁饼1个,莲蓉饼1个,豆沙饼2个,每种包装每盒月饼的成本价为该盒中所有月饼的成本价之和.已知每个五仁饼与每个莲蓉饼的成本价之比为5:4,每盒乙包装月饼售价98元,利润率是40%,两种包装的月饼共50盒总价6123元,总利润率是30%.中秋节后,为降价促销,甲种包装每盒每类月饼各少装一个,乙种包装每盒少装月饼后售价降为原来的一半,利润率不变,那么这样包装的两种月饼共50盒的总成本是
元(其中甲种包装少装月饼后的盒数与节前50盒中甲种包装月饼的盒数相同,当然乙种包装盒数也相同).
13.(2019?雨城区校级模拟)若数a使关于x的不等式组有且只有四个整数解,且使关于y的方程=2的解为非负数,则符合条件的所有整数a的和为
.
14.(2014春?青羊区期末)已知x2﹣5x+1=0,则的值是
.
15.(2009春?营山县期末)已知,则=
.
16.已知实数x,y,z,a满足x+a2=2010,y+a2=2011,z+a2=2012,且xyz=6,则代数式++﹣﹣﹣的值等于
.
17.“非洲猪瘟”本是一种只在家畜之间传播的瘟疫,但最近已严重威胁到广大人民群众的生命安全,现我市有一组检疫工作人员(工作人员每人每天生猪检疫的效率相等),需对甲、乙两个生猪养殖场的所有生猪逐一检疫,已知,甲养殖场的生猪比乙养殖场的生猪多1倍.上午全部工作人员在甲养殖场检疫,为了尽快完成检疫,下午所有工作人员的平均工作效率提高了20%,但下午有一人因事离开,剩下的工作人员的一半仍留在甲养殖场(上、下午的工作时间相等),到下班前刚好把甲养殖场的生猪检疫完毕,另一半工作人员去乙养殖场检疫,到下班前还剩下一小部分生猪未检疫,最后由6人以提高前的检疫速度,再用不到半天的工作时间就完成了检疫.则这组工作人员最多有
人.
18.(2021?九龙坡区模拟)临近端午,甲、乙两生产商分别承接制作白粽,豆沙粽和蛋黄粽的任务(三种粽子都有成品,甲生产商安排200名工人制作白粽和豆沙粽,每人只能制作其中一种粽子,乙生产商安排100名工人制作蛋黄粽,其中豆沙粽的人均制作数量比白粽的人均制作数量少15个,蛋黄粽的人均制作数量比豆沙粽的人均制作数量少20%,若本次制作的白粽、豆沙粽和蛋黄粽三种粽子的人均制作数量比白粽的人均制作数用少20%,且豆沙粽的人均制作量为偶数个,则本次可制作的粽子数量最多为
个.
19.(2020秋?北京期末)依据如图流程图计算﹣,需要经历的路径是
(只填写序号),输出的运算结果是
.
20.设2016a3=2017b3=2018c3,abc>0,且=++,则++=
三.解答题(共10小题)
21.(2021?包河区三模)市政府为美化城市环境,计划在某区城种植树木2000棵,由于青年志愿者的加入,实际每天植树棵数是原计划的2倍,结果提前4天完成任务.求实际每天植树多少棵?
22.(2021?平房区三模)某体育用品商店计划购进一些篮球和排球.已知每个篮球的进价和每个排球的进价的和为200元,用2400元购进的篮球数量是用800元购进排球数量的2倍.
(1)求每个篮球和每个排球的进价各是多少元;
(2)若该体育用品商店计划购进篮球和排球共40个,且购进的总费用不超过3800元,则该体育用品商店最多可以购进篮球多少个?
23.(2021?岳阳二模)岳阳市区某中学为了创建“书香校园”,今年春季购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元,已知学校用20000元购买的科普类图书的本数与用15000元购买的文学类图书的本数相等.
(1)求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
(2)学校计划在五月份再添置600本这两类图书,且费用不超过10000元,问最多可以购买科普类图书多少本?
24.(2021?宝安区模拟)为了抗击“新型肺炎”,我市某医药器械厂接受了生产一批高质量医用口罩的任务,任务要求在30天之内(含30天)生产A型和B型两种型号的口罩共200万只.在实际生产中,由于受条件限制,该工厂每天只能生产一种型号的口罩.已知该工厂每天可生产A型口罩的个数是生产B型口罩的2倍,并且加工生产40万只A型口罩比加工生产50万只B型口罩少用6天.
(1)该工厂每天可加工生产多少万只B型口罩?
(2)若生产一只A型口罩的利润是0.8元,生产一只B型口罩的利润是1.2元,在确保准时交付的情况下,如何安排工厂生产可以使生产这批口罩的利润最大?
25.(2020秋?香洲区期末)已知(x+a)(x+b)=x2+mx+n.
(1)若a=﹣3,b=2,则m=
,n=
;
(2)若m=﹣2,,求的值;
(3)若n=﹣1,当时,求m的值.
26.(2021春?滨湖区期中)小红、小刚、小明三位同学在讨论:当x取何整数时,分式的值是整数?
小红说:这个分式的分子、分母都含有x,它们的值均随x取值的变化而变化,有点难.
小刚说:我会解这类问题:当x取何整数时,分式的值是整数?3是x+1的整数倍即可,注意不要忘记负数哦.
小明说:可将分式与分数进行类比.本题可以类比小学里学过的“假分数”,当分子大于分母时,可以将“假分数”化为一个整数与“真分数”的和.比如:==2+(通常写成带分数:2).类比分式,当分子的次数大于或等于分母次数时,可称这样的分式为“假分式”,若将化成一个整式与一个“真分式”的和,就转化成小刚说的那类问题了!
小红、小刚说:对!我们试试看!…
(1)解决小刚提出的问题;
(2)解决他们共同讨论的问题.
27.(2021春?大兴区期中)已知非零实数a、b满足等式,求的值.
28.(2020秋?连山区期末)阅读下面的材料,并解答后面的问题
材料:将分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式.
解:由分母为x+1,可设3x2+4x﹣1=(x+1)(3x+a)+b.
因为(x+1)(3x+a)+b=3x2+ax+3x+a+b=3x2+(a+3)x+a+b,
所以3x2+4x﹣1=3x2+(a+3)x+a+b.
所以,解得.
所以==﹣=3x+1﹣.
这样,分式就被拆分成了一个整式3x+1与一个分式的差的形式.
根据你的理解解决下列问题:
(1)请将分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式;
(2)若分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式为:5m﹣11+,求m2+n2+mn的最小值.
29.(2020秋?乌苏市期末)近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路商业运营树立了新的标杆.随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,跑出发展新速度,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从A地到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为多少千米?
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
30.(2021?禅城区校级一模)先化简(1﹣)÷,再从0,2,﹣1,1中选择一个合适的数代入并求值.
北师大新版数学专题复习《分式与分式方程》
参考答案与试题解析
一.选择题(共10小题)
1.(2021?十堰)某工厂现在平均每天比原计划多生产50台机器,现在生产400台机器所需时间比原计划生产450台机器所需时间少1天,设现在平均每天生产x台机器,则下列方程正确的是( )
A.﹣=1
B.﹣=1
C.﹣=50
D.﹣=50
【解答】解:设现在平均每天生产x台机器,则原计划平均每天生产(x﹣50)台机器,
根据题意,得﹣=1.
故选:B.
2.(2021?嘉兴)为迎接建党一百周年,某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威,其中缤纷棒共花费30元,荧光棒共花费40元,缤纷棒比荧光棒少20根,缤纷棒单价是荧光棒的1.5倍.若设荧光棒的单价为x元,根据题意可列方程为( )
A.﹣=20
B.﹣=20
C.﹣=20
D.﹣=20
【解答】解:若设荧光棒的单价为x元,则缤纷棒单价是1.5x元,
根据题意可得:﹣=20.
故选:B.
3.(2021?重庆)若关于x的一元一次不等式组的解集为x≥6,且关于y的分式方程+=2的解是正整数,则所有满足条件的整数a的值之和是( )
A.5
B.8
C.12
D.15
【解答】解:,
解不等式①得:x≥6,
解不等式②得:x>,
∵不等式组的解集为x≥6,
∴6,
∴a<7;
分式方程两边都乘(y﹣1)得:y+2a﹣3y+8=2(y﹣1),
解得:y=,
∵方程的解是正整数,
∴>0,
∴a>﹣5;
∵y﹣1≠0,
∴1,
∴a≠﹣3,
∴﹣5<a<7,且a≠﹣3,
∴能使是正整数的a是:﹣1,1,3,5,
∴和为8,
故选:B.
4.(2021春?沙坪坝区校级月考)已知关于x的不等式组有解,且关于y的分式方程=4﹣有正整数解,则所有满足条件的整数a的值的个数为( )
A.2
B.3
C.4
D.5
【解答】解:
解不等式①得x<2,
解不等式②得x>﹣1,
∵不等式组有解,
∴﹣1<2,
解得a<9,
解分式方程=4﹣得y=,
∵方程的解为正数,
∴>0且≠3,
∴a>﹣且a≠3,
∴﹣<a<9且a≠3,
满足使方程的解为正整数的整数a的值有0,6两个.
故选:A.
5.(2021春?茅箭区月考)某施工队计划修建一个长为600米的隧道,第一周按原计划的速度修建,一周后以原来速度的1.5倍修建,结果比原计划提前一周完成任务,若设原计划一周修建隧道x米,则可列方程为( )
A.=+2
B.=﹣2
C.=+1
D.=﹣1
【解答】解:设原计划一周修建隧道x米,则提速后的速度为一周修建1.5x米,
根据题意,得:=+1.
故选:C.
6.(2021?铜梁区校级一模)若整数a使关于x的不等式组有且只有两个整数解,且关于y的分式方程﹣=﹣2的解为正数,则满足上述条件的a的和为( )
A.3
B.4
C.5
D.6
【解答】解:,
解不等式①得:x≤2,
解不等式②得:x≥,
∴不等式组的解集为≤x≤2,
∵不等式组有且只有两个整数解,
∴0<≤1,
∴0<a≤3;
分式方程两边都乘以(y﹣1)得:1﹣3y+2a=﹣2(y﹣1),
解得:y=2a﹣1,
∵分式方程的解为正数,
∴2a﹣1>0,
∴a>;
∵y﹣1≠0,
∴y≠1,
∴2a﹣1≠1,
∴a≠1,
∴<a≤3,且a≠1,
∵a是整数,
∴a=2或3,
∴2+3=5,
故选:C.
7.(2021?九龙坡区校级模拟)若数m使关于x的不等式组有解且至多有3个整数解,且使关于x的分式方程有整数解,则满足条件的所有整数m的个数是( )
A.5
B.4
C.3
D.2
【解答】解:,
解不等式①得:x≥﹣1,
∴﹣1≤x<,
∵不等式组有解且至多3个整数解,
∴﹣1<<2,
∴﹣3<m<6,
分式方程两边都乘以(x﹣1)得:mx﹣2﹣3=2(x﹣1),
∴(m﹣2)x=3,
当m≠2时,x=,
∵x﹣1≠0,
∴x≠1,
∴≠1,
∴m≠5,
∵方程有整数解,
∴m﹣2=±1,±3,
解得:m=3,1,5,﹣1,
∵m≠5,
∴,m=3,1,﹣1.
故选:C.
8.(2021春?重庆月考)若关于x的一元一次不等式组有且仅有3个整数解,且关于x的分式方程+=1有正数解,则所有满足条件的整数a的和为( )
A.12
B.13
C.14
D.15
【解答】解:,
解不等式①得:x<5,
解不等式②得:x≥,
∴不等式组的解集为,
∵不等式组有且仅有3个整数解,
∴1<≤2,
∴2<a≤6;
分式方程两边都乘以(x﹣1)得:ax﹣2﹣3=x﹣1,
解得:x=,
∵x﹣1≠0,
∴x≠1,
∵方程有正数解,
∴0,≠1,
∴a>1,a≠5,
∴2<a≤6,且a≠5,
∴a的整数解为3,4,6,和为13,
故选:B.
9.(2018春?温州期末)甲、乙、丙三名打字员承担一项打字任务,已知如下信息
如果每小时只安排1名打字员,那么按照甲、乙、丙的顺序至完成工作任务,共需( )
A.13小时
B.13小时
C.14小时
D.14小时
【解答】解:设甲单独完成任务需要x小时,则乙单独完成任务需要(x﹣5)小时,则
=.
解得x=20
经检验x=20是原方程的根,且符合题意.
则丙的工作效率是.
所以一轮的工作量为:++=.
所以4轮后剩余的工作量为:1﹣=.
所以还需要甲、乙分别工作1小时后,丙需要的工作量为:﹣﹣=.
所以丙还需要工作小时.
故一共需要的时间是:3×4+2+=14小时.
故选:C.
10.设x<0,x﹣=,则代数式的值( )
A.1
B.
C.
D.
【解答】解:∵x﹣=,
∴(x)2=5,
∴x2+=7,
∴(x+)2=x2+2+=9,
∵x<0,
∴x+=﹣3,
∴x2+1=﹣3x,
∴x4+1=7x2,
∵(x2+)2=x4+2+,
∴x4+=47,
∴x8+1=47x4,
∵x3+=(x+)(x2﹣1+),
∴x3+=﹣18,
∴x6+1=﹣18x3,
∴原式=
=
=
=
=
故选:B.
二.填空题(共10小题)
11.(2020秋?锦江区校级月考)若关于x的一元一次不等式组的解集为x≥5,且关于y的分式方程+=﹣1有非负整数解,则符合条件的所有整数a的和为 ﹣2 .
【解答】解:,
解不等式①得:x≥5,
解不等式②得:x>a+2,
∵解集为x≥5,
∴a+2<5,
∴a<3;
分式方程两边都乘以(y﹣2)得:y﹣a=﹣(y﹣2),
解得:y=,
∵分式方程有非负整数解,
∴≥0,
∴a≥﹣2,
∵≠2,
∴a≠2,
综上所述,﹣2≤a<3且a≠2,
∴符合条件的所有整数a的数有:﹣2,﹣1,0,1,
和为﹣2﹣1+0+1=﹣2.
故答案为:﹣2.
12.(2020秋?沙坪坝区校级月考)中秋、国庆“双节”前,某酒店推出甲,乙两种包装的月饼,其中甲种包装有五仁饼3个,莲蓉饼3个,豆沙饼2个,乙种包装有五仁饼1个,莲蓉饼1个,豆沙饼2个,每种包装每盒月饼的成本价为该盒中所有月饼的成本价之和.已知每个五仁饼与每个莲蓉饼的成本价之比为5:4,每盒乙包装月饼售价98元,利润率是40%,两种包装的月饼共50盒总价6123元,总利润率是30%.中秋节后,为降价促销,甲种包装每盒每类月饼各少装一个,乙种包装每盒少装月饼后售价降为原来的一半,利润率不变,那么这样包装的两种月饼共50盒的总成本是 4710 元(其中甲种包装少装月饼后的盒数与节前50盒中甲种包装月饼的盒数相同,当然乙种包装盒数也相同).
【解答】解:设乙的成本价为a,
根据题意列出90﹣s=40%a,
解得a=70,
设五仁饼的成本价为x,则一个莲蓉饼的成本价,则两豆沙饼成本价为(70﹣),
设甲礼盒和乙礼盒分别为m盒和n盒,m+n=50
则有70n+m(3x+3×)=6213÷(1+30%)
70n+70m+mx=4710.
xm=,
节后乙每盒成本98÷2÷(1+40%)=35,
甲每盒成本2x+2×x+35﹣x=35+x,
总成本35n+m(35+x)=35×50+×=2657.5.
故答案为:2657.5.
13.(2019?雨城区校级模拟)若数a使关于x的不等式组有且只有四个整数解,且使关于y的方程=2的解为非负数,则符合条件的所有整数a的和为 1 .
【解答】解:,
解①得,x<5;
解②得,
∴不等式组的解集为;
∵不等式有且只有四个整数解,
∴,
解得,﹣2<a≤2;
解分式方程得,y=2﹣a(a≠1);
∵方程的解为非负数,
∴2﹣a≥0即a≤2且a≠1
综上可知,﹣2<a≤2且a≠1,
∵a是整数,
∴a=﹣1,0,2;
∴﹣1+0+2=1,
故答案为:1.
14.(2014春?青羊区期末)已知x2﹣5x+1=0,则的值是 .
【解答】解:∵x2﹣5x+1=0,
∴x2=5x﹣1,
∴原式=
=
=
=
=
=.
故答案为:.
15.(2009春?营山县期末)已知,则= ﹣ .
【解答】解:∵﹣=2,
∴=2,即x﹣y=﹣2xy,
原式=
=
=
=﹣.
故答案为:﹣.
16.已知实数x,y,z,a满足x+a2=2010,y+a2=2011,z+a2=2012,且xyz=6,则代数式++﹣﹣﹣的值等于 .
【解答】解:∵xyz=6,
∴++﹣﹣﹣
=﹣
=﹣
=
=[(x﹣y)2+(y﹣z)2+(x﹣z)2],
∵x+a2=2010,y+a2=2011,z+a2=2012,
∴x﹣y=﹣1,y﹣z=﹣1,x﹣z=﹣2,
∴原式=×[(﹣1)2+(﹣1)2+(﹣2)2]=×(1+1+4)==,
故答案为:.
17.“非洲猪瘟”本是一种只在家畜之间传播的瘟疫,但最近已严重威胁到广大人民群众的生命安全,现我市有一组检疫工作人员(工作人员每人每天生猪检疫的效率相等),需对甲、乙两个生猪养殖场的所有生猪逐一检疫,已知,甲养殖场的生猪比乙养殖场的生猪多1倍.上午全部工作人员在甲养殖场检疫,为了尽快完成检疫,下午所有工作人员的平均工作效率提高了20%,但下午有一人因事离开,剩下的工作人员的一半仍留在甲养殖场(上、下午的工作时间相等),到下班前刚好把甲养殖场的生猪检疫完毕,另一半工作人员去乙养殖场检疫,到下班前还剩下一小部分生猪未检疫,最后由6人以提高前的检疫速度,再用不到半天的工作时间就完成了检疫.则这组工作人员最多有 27 人.
【解答】解:设每人每天可检疫x头猪,该组检疫工作人员有y人,由题意得:
xy+x(1+20%)×<2[x(1+20%)×+6×],
化简得:0.4y<11.4
∴y<28.5,
∵y只能为正整数,且有一人离开后,人数平分
∴y的最大值为27.
故答案为:27.
18.(2021?九龙坡区模拟)临近端午,甲、乙两生产商分别承接制作白粽,豆沙粽和蛋黄粽的任务(三种粽子都有成品,甲生产商安排200名工人制作白粽和豆沙粽,每人只能制作其中一种粽子,乙生产商安排100名工人制作蛋黄粽,其中豆沙粽的人均制作数量比白粽的人均制作数量少15个,蛋黄粽的人均制作数量比豆沙粽的人均制作数量少20%,若本次制作的白粽、豆沙粽和蛋黄粽三种粽子的人均制作数量比白粽的人均制作数用少20%,且豆沙粽的人均制作量为偶数个,则本次可制作的粽子数量最多为 23760 个.
【解答】解:设生产豆沙粽的有x人,白粽子的有(200﹣x)人;生产豆沙粽人均y个,白粽子人均(y+15)个,则蛋黄粽子人均y(1﹣20%)=0.8y个.
由题意得[xy+(y+15)(200﹣x)+100×0.8y]×=(y+15)×(1﹣20%),
∴(xy+200y+3000﹣xy﹣15x+80y)×=0.8y+12,
∴y+10﹣x=0.8y+12,
∴y﹣x=2,
∴x=y﹣40.
又∵200﹣x>0,y>0,
∴0<y<90.
∵需要制作的粽子最多,而粽子总数为300(0.8y+12),y是偶数
∴y=84时,x=184,制作的粽子最多为23760.
故答案为:23760.
19.(2020秋?北京期末)依据如图流程图计算﹣,需要经历的路径是 ② (只填写序号),输出的运算结果是 .
【解答】解:∵两个分式分母不同,
∴经历路径为②.
根据路径②计算如下:
原式=,
=﹣,
=,
故答案为:②,.
20.设2016a3=2017b3=2018c3,abc>0,且=++,则++= 1
【解答】解:===(),
++=+=(),
即:=,解得:=1.
故答案为1.
三.解答题(共10小题)
21.(2021?包河区三模)市政府为美化城市环境,计划在某区城种植树木2000棵,由于青年志愿者的加入,实际每天植树棵数是原计划的2倍,结果提前4天完成任务.求实际每天植树多少棵?
【解答】解:设原计划每天植树x棵,则实际每天植树棵数是2x棵,
根据题意,得﹣=4.
解得x=250.
经检验x=250是原方程的解,且符合题意.
所以2x=500.
答:实际每天植树500棵.
22.(2021?平房区三模)某体育用品商店计划购进一些篮球和排球.已知每个篮球的进价和每个排球的进价的和为200元,用2400元购进的篮球数量是用800元购进排球数量的2倍.
(1)求每个篮球和每个排球的进价各是多少元;
(2)若该体育用品商店计划购进篮球和排球共40个,且购进的总费用不超过3800元,则该体育用品商店最多可以购进篮球多少个?
【解答】解:(1)设每个篮球的进价为x元,则每个排球的进价为(200﹣x)元.
根据题意得.
解得x=120.
经检验x=120是原分式方程的解.
∴200﹣x=200﹣120=80(元).
答:每个篮球的进价为120元,每个排球的进价为80元.
(2)设该体育用品商店可以购进篮球a个,则购进排球(40﹣a)个,
根据题意,得120a+80(40﹣a)≤3800.
解得a≤15.
答:该体育用品商店最多可以购进篮球15个.
23.(2021?岳阳二模)岳阳市区某中学为了创建“书香校园”,今年春季购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元,已知学校用20000元购买的科普类图书的本数与用15000元购买的文学类图书的本数相等.
(1)求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
(2)学校计划在五月份再添置600本这两类图书,且费用不超过10000元,问最多可以购买科普类图书多少本?
【解答】解:(1)设科普类书的单价为x元/本,则文学类书的单价为(x﹣5)元/本,
依题意:,
解之得:x=20.
经检验,x=20是所列分程的根,且合实际,
∴x﹣5=15.
答:科普类书单价为20元/本,文学类书单价为15元/本;
(2)设科普类书购a本,则文学类书购(600﹣a)本,
依题意:20a+15(600﹣a)≤10000,
解之得:a≤200.
答:最多可购科普类图书200本.
24.(2021?宝安区模拟)为了抗击“新型肺炎”,我市某医药器械厂接受了生产一批高质量医用口罩的任务,任务要求在30天之内(含30天)生产A型和B型两种型号的口罩共200万只.在实际生产中,由于受条件限制,该工厂每天只能生产一种型号的口罩.已知该工厂每天可生产A型口罩的个数是生产B型口罩的2倍,并且加工生产40万只A型口罩比加工生产50万只B型口罩少用6天.
(1)该工厂每天可加工生产多少万只B型口罩?
(2)若生产一只A型口罩的利润是0.8元,生产一只B型口罩的利润是1.2元,在确保准时交付的情况下,如何安排工厂生产可以使生产这批口罩的利润最大?
【解答】解:(1)设工厂每天可加工生产x万只B型口罩,则
.
解得x=5.
经检验x=5是原方程的根.
答:该工厂每天可生产5万只B型口罩.
(2)设安排工厂生产A型口罩a万只,则生产B型口罩(200﹣a)万只,这批口罩的总利润为W万元,则有:
W=0.8a+1.2(200﹣a)=﹣0.4a+240.
∵要确保准时交付,
∴.
∵k=﹣0.4<0,W随a的增大而减小,
∴当a=100时,W最大=200万元.
答:应该安排该工厂生产100万只A型口罩,100万只B型口罩时利润最大.
25.(2020秋?香洲区期末)已知(x+a)(x+b)=x2+mx+n.
(1)若a=﹣3,b=2,则m= ﹣1 ,n= ﹣6 ;
(2)若m=﹣2,,求的值;
(3)若n=﹣1,当时,求m的值.
【解答】解:(1)将a=﹣3,b=2代入(x+a)(x+b)得:
(x+a)(x+b)=(x﹣3)(x+2)=x2﹣x﹣6=x2+mx+n,
∴m=﹣1,n=﹣6.
故答案为:﹣1,﹣6.
(2)∵(x+a)(x+b)=x2+(a+b)x+ab=x2+mx+n.
∴,
∴+====﹣4.
(3)∵a+b=m,ab=n=﹣1,,
∴,
∴,
∴,
∴m2﹣2×(﹣1)+4m+2=0,
∴m2+4m+4=0,
∴(m+2)2=0,
∴m=﹣2.
26.(2021春?滨湖区期中)小红、小刚、小明三位同学在讨论:当x取何整数时,分式的值是整数?
小红说:这个分式的分子、分母都含有x,它们的值均随x取值的变化而变化,有点难.
小刚说:我会解这类问题:当x取何整数时,分式的值是整数?3是x+1的整数倍即可,注意不要忘记负数哦.
小明说:可将分式与分数进行类比.本题可以类比小学里学过的“假分数”,当分子大于分母时,可以将“假分数”化为一个整数与“真分数”的和.比如:==2+(通常写成带分数:2).类比分式,当分子的次数大于或等于分母次数时,可称这样的分式为“假分式”,若将化成一个整式与一个“真分式”的和,就转化成小刚说的那类问题了!
小红、小刚说:对!我们试试看!…
(1)解决小刚提出的问题;
(2)解决他们共同讨论的问题.
【解答】解:(1)当x+1=±1,±3时,分式的值是整数,
∴x=0,﹣2,2,﹣4.
(2)=3﹣,
当x+1=±1,±5时,分式的值为整数,
∴x=0,﹣2,4,﹣6.
27.(2021春?大兴区期中)已知非零实数a、b满足等式,求的值.
【解答】解:等式两边都乘以ab得:b2+a2+5=4a+2b,
整理得:(b﹣1)2+(a﹣2)2=0,
∴a=2,b=1,
代入得:
原式=.
28.(2020秋?连山区期末)阅读下面的材料,并解答后面的问题
材料:将分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式.
解:由分母为x+1,可设3x2+4x﹣1=(x+1)(3x+a)+b.
因为(x+1)(3x+a)+b=3x2+ax+3x+a+b=3x2+(a+3)x+a+b,
所以3x2+4x﹣1=3x2+(a+3)x+a+b.
所以,解得.
所以==﹣=3x+1﹣.
这样,分式就被拆分成了一个整式3x+1与一个分式的差的形式.
根据你的理解解决下列问题:
(1)请将分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式;
(2)若分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式为:5m﹣11+,求m2+n2+mn的最小值.
【解答】解:(1)由分母为x﹣1,可设2x2+3x+6=(x﹣1)(2x+a)+b.
因为(x﹣1)(2x+a)+b=2x2+ax﹣2x﹣a+b=2x2+(a﹣2)x﹣a+b,
所以2x2+3x+6=2x2+(a﹣2)x﹣a+b,
因此有,
解得,
所以==2x+5+;
(2)由分母为x+2,可设5x2+9x﹣3=(x+2)(5x+a)+b,
因为(x+2)(5x+a)+b=5x2+ax+10x+2a+b=5x2+(a+10)x+2a+b,
所以5x2+9x﹣3=5x2+(a+10)x+2a+b,
因此有,
解得,
所以==5x﹣1﹣,
所以5m﹣11+=5x﹣1﹣,
因此5m﹣11=5x﹣1,n﹣6=﹣x﹣2,
所以m=x+2,n=﹣x+4,
所以m2+n2+mn=x2﹣2x+28=(x﹣1)2+27,
因为(x﹣1)2≥0,所以(x﹣1)2+27≥27,
所以m2+n2+mn的最小值为27.
29.(2020秋?乌苏市期末)近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路商业运营树立了新的标杆.随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,跑出发展新速度,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从A地到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为多少千米?
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
【解答】解:(1)普通列车的行驶路程为:400×1.3=520(千米);
(2)设普通列车的平均速度为x千米/时,则高铁的平均速度为2.5千米/时,则题意得:
=﹣3,
解得:x=120,
经检验x=120是原方程的解,
则高铁的平均速度是120×2.5=300(千米/时),
答:普通列车的平均速度是120千米/时,高铁的平均速度是300千米/时.
30.(2021?禅城区校级一模)先化简(1﹣)÷,再从0,2,﹣1,1中选择一个合适的数代入并求值.
【解答】解:原式=×=.
因为x不能取±1,2,
所以把x=0代入,原式==﹣.
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
北师大新版数学专题复习《分式与分式方程》
一.选择题(共10小题)
1.(2021?十堰)某工厂现在平均每天比原计划多生产50台机器,现在生产400台机器所需时间比原计划生产450台机器所需时间少1天,设现在平均每天生产x台机器,则下列方程正确的是( )
A.﹣=1
B.﹣=1
C.﹣=50
D.﹣=50
2.(2021?嘉兴)为迎接建党一百周年,某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威,其中缤纷棒共花费30元,荧光棒共花费40元,缤纷棒比荧光棒少20根,缤纷棒单价是荧光棒的1.5倍.若设荧光棒的单价为x元,根据题意可列方程为( )
A.﹣=20
B.﹣=20
C.﹣=20
D.﹣=20
3.(2021?重庆)若关于x的一元一次不等式组的解集为x≥6,且关于y的分式方程+=2的解是正整数,则所有满足条件的整数a的值之和是( )
A.5
B.8
C.12
D.15
4.(2021春?沙坪坝区校级月考)已知关于x的不等式组有解,且关于y的分式方程=4﹣有正整数解,则所有满足条件的整数a的值的个数为( )
A.2
B.3
C.4
D.5
5.(2021春?茅箭区月考)某施工队计划修建一个长为600米的隧道,第一周按原计划的速度修建,一周后以原来速度的1.5倍修建,结果比原计划提前一周完成任务,若设原计划一周修建隧道x米,则可列方程为( )
A.=+2
B.=﹣2
C.=+1
D.=﹣1
6.(2021?铜梁区校级一模)若整数a使关于x的不等式组有且只有两个整数解,且关于y的分式方程﹣=﹣2的解为正数,则满足上述条件的a的和为( )
A.3
B.4
C.5
D.6
7.(2021?九龙坡区校级模拟)若数m使关于x的不等式组有解且至多有3个整数解,且使关于x的分式方程有整数解,则满足条件的所有整数m的个数是( )
A.5
B.4
C.3
D.2
8.(2021春?重庆月考)若关于x的一元一次不等式组有且仅有3个整数解,且关于x的分式方程+=1有正数解,则所有满足条件的整数a的和为( )
A.12
B.13
C.14
D.15
9.(2018春?温州期末)甲、乙、丙三名打字员承担一项打字任务,已知如下信息
如果每小时只安排1名打字员,那么按照甲、乙、丙的顺序至完成工作任务,共需( )
A.13小时
B.13小时
C.14小时
D.14小时
10.设x<0,x﹣=,则代数式的值( )
A.1
B.
C.
D.
二.填空题(共10小题)
11.(2020秋?锦江区校级月考)若关于x的一元一次不等式组的解集为x≥5,且关于y的分式方程+=﹣1有非负整数解,则符合条件的所有整数a的和为
.
12.(2020秋?沙坪坝区校级月考)中秋、国庆“双节”前,某酒店推出甲,乙两种包装的月饼,其中甲种包装有五仁饼3个,莲蓉饼3个,豆沙饼2个,乙种包装有五仁饼1个,莲蓉饼1个,豆沙饼2个,每种包装每盒月饼的成本价为该盒中所有月饼的成本价之和.已知每个五仁饼与每个莲蓉饼的成本价之比为5:4,每盒乙包装月饼售价98元,利润率是40%,两种包装的月饼共50盒总价6123元,总利润率是30%.中秋节后,为降价促销,甲种包装每盒每类月饼各少装一个,乙种包装每盒少装月饼后售价降为原来的一半,利润率不变,那么这样包装的两种月饼共50盒的总成本是
元(其中甲种包装少装月饼后的盒数与节前50盒中甲种包装月饼的盒数相同,当然乙种包装盒数也相同).
13.(2019?雨城区校级模拟)若数a使关于x的不等式组有且只有四个整数解,且使关于y的方程=2的解为非负数,则符合条件的所有整数a的和为
.
14.(2014春?青羊区期末)已知x2﹣5x+1=0,则的值是
.
15.(2009春?营山县期末)已知,则=
.
16.已知实数x,y,z,a满足x+a2=2010,y+a2=2011,z+a2=2012,且xyz=6,则代数式++﹣﹣﹣的值等于
.
17.“非洲猪瘟”本是一种只在家畜之间传播的瘟疫,但最近已严重威胁到广大人民群众的生命安全,现我市有一组检疫工作人员(工作人员每人每天生猪检疫的效率相等),需对甲、乙两个生猪养殖场的所有生猪逐一检疫,已知,甲养殖场的生猪比乙养殖场的生猪多1倍.上午全部工作人员在甲养殖场检疫,为了尽快完成检疫,下午所有工作人员的平均工作效率提高了20%,但下午有一人因事离开,剩下的工作人员的一半仍留在甲养殖场(上、下午的工作时间相等),到下班前刚好把甲养殖场的生猪检疫完毕,另一半工作人员去乙养殖场检疫,到下班前还剩下一小部分生猪未检疫,最后由6人以提高前的检疫速度,再用不到半天的工作时间就完成了检疫.则这组工作人员最多有
人.
18.(2021?九龙坡区模拟)临近端午,甲、乙两生产商分别承接制作白粽,豆沙粽和蛋黄粽的任务(三种粽子都有成品,甲生产商安排200名工人制作白粽和豆沙粽,每人只能制作其中一种粽子,乙生产商安排100名工人制作蛋黄粽,其中豆沙粽的人均制作数量比白粽的人均制作数量少15个,蛋黄粽的人均制作数量比豆沙粽的人均制作数量少20%,若本次制作的白粽、豆沙粽和蛋黄粽三种粽子的人均制作数量比白粽的人均制作数用少20%,且豆沙粽的人均制作量为偶数个,则本次可制作的粽子数量最多为
个.
19.(2020秋?北京期末)依据如图流程图计算﹣,需要经历的路径是
(只填写序号),输出的运算结果是
.
20.设2016a3=2017b3=2018c3,abc>0,且=++,则++=
三.解答题(共10小题)
21.(2021?包河区三模)市政府为美化城市环境,计划在某区城种植树木2000棵,由于青年志愿者的加入,实际每天植树棵数是原计划的2倍,结果提前4天完成任务.求实际每天植树多少棵?
22.(2021?平房区三模)某体育用品商店计划购进一些篮球和排球.已知每个篮球的进价和每个排球的进价的和为200元,用2400元购进的篮球数量是用800元购进排球数量的2倍.
(1)求每个篮球和每个排球的进价各是多少元;
(2)若该体育用品商店计划购进篮球和排球共40个,且购进的总费用不超过3800元,则该体育用品商店最多可以购进篮球多少个?
23.(2021?岳阳二模)岳阳市区某中学为了创建“书香校园”,今年春季购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元,已知学校用20000元购买的科普类图书的本数与用15000元购买的文学类图书的本数相等.
(1)求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
(2)学校计划在五月份再添置600本这两类图书,且费用不超过10000元,问最多可以购买科普类图书多少本?
24.(2021?宝安区模拟)为了抗击“新型肺炎”,我市某医药器械厂接受了生产一批高质量医用口罩的任务,任务要求在30天之内(含30天)生产A型和B型两种型号的口罩共200万只.在实际生产中,由于受条件限制,该工厂每天只能生产一种型号的口罩.已知该工厂每天可生产A型口罩的个数是生产B型口罩的2倍,并且加工生产40万只A型口罩比加工生产50万只B型口罩少用6天.
(1)该工厂每天可加工生产多少万只B型口罩?
(2)若生产一只A型口罩的利润是0.8元,生产一只B型口罩的利润是1.2元,在确保准时交付的情况下,如何安排工厂生产可以使生产这批口罩的利润最大?
25.(2020秋?香洲区期末)已知(x+a)(x+b)=x2+mx+n.
(1)若a=﹣3,b=2,则m=
,n=
;
(2)若m=﹣2,,求的值;
(3)若n=﹣1,当时,求m的值.
26.(2021春?滨湖区期中)小红、小刚、小明三位同学在讨论:当x取何整数时,分式的值是整数?
小红说:这个分式的分子、分母都含有x,它们的值均随x取值的变化而变化,有点难.
小刚说:我会解这类问题:当x取何整数时,分式的值是整数?3是x+1的整数倍即可,注意不要忘记负数哦.
小明说:可将分式与分数进行类比.本题可以类比小学里学过的“假分数”,当分子大于分母时,可以将“假分数”化为一个整数与“真分数”的和.比如:==2+(通常写成带分数:2).类比分式,当分子的次数大于或等于分母次数时,可称这样的分式为“假分式”,若将化成一个整式与一个“真分式”的和,就转化成小刚说的那类问题了!
小红、小刚说:对!我们试试看!…
(1)解决小刚提出的问题;
(2)解决他们共同讨论的问题.
27.(2021春?大兴区期中)已知非零实数a、b满足等式,求的值.
28.(2020秋?连山区期末)阅读下面的材料,并解答后面的问题
材料:将分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式.
解:由分母为x+1,可设3x2+4x﹣1=(x+1)(3x+a)+b.
因为(x+1)(3x+a)+b=3x2+ax+3x+a+b=3x2+(a+3)x+a+b,
所以3x2+4x﹣1=3x2+(a+3)x+a+b.
所以,解得.
所以==﹣=3x+1﹣.
这样,分式就被拆分成了一个整式3x+1与一个分式的差的形式.
根据你的理解解决下列问题:
(1)请将分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式;
(2)若分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式为:5m﹣11+,求m2+n2+mn的最小值.
29.(2020秋?乌苏市期末)近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路商业运营树立了新的标杆.随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,跑出发展新速度,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从A地到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为多少千米?
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
30.(2021?禅城区校级一模)先化简(1﹣)÷,再从0,2,﹣1,1中选择一个合适的数代入并求值.
北师大新版数学专题复习《分式与分式方程》
参考答案与试题解析
一.选择题(共10小题)
1.(2021?十堰)某工厂现在平均每天比原计划多生产50台机器,现在生产400台机器所需时间比原计划生产450台机器所需时间少1天,设现在平均每天生产x台机器,则下列方程正确的是( )
A.﹣=1
B.﹣=1
C.﹣=50
D.﹣=50
【解答】解:设现在平均每天生产x台机器,则原计划平均每天生产(x﹣50)台机器,
根据题意,得﹣=1.
故选:B.
2.(2021?嘉兴)为迎接建党一百周年,某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威,其中缤纷棒共花费30元,荧光棒共花费40元,缤纷棒比荧光棒少20根,缤纷棒单价是荧光棒的1.5倍.若设荧光棒的单价为x元,根据题意可列方程为( )
A.﹣=20
B.﹣=20
C.﹣=20
D.﹣=20
【解答】解:若设荧光棒的单价为x元,则缤纷棒单价是1.5x元,
根据题意可得:﹣=20.
故选:B.
3.(2021?重庆)若关于x的一元一次不等式组的解集为x≥6,且关于y的分式方程+=2的解是正整数,则所有满足条件的整数a的值之和是( )
A.5
B.8
C.12
D.15
【解答】解:,
解不等式①得:x≥6,
解不等式②得:x>,
∵不等式组的解集为x≥6,
∴6,
∴a<7;
分式方程两边都乘(y﹣1)得:y+2a﹣3y+8=2(y﹣1),
解得:y=,
∵方程的解是正整数,
∴>0,
∴a>﹣5;
∵y﹣1≠0,
∴1,
∴a≠﹣3,
∴﹣5<a<7,且a≠﹣3,
∴能使是正整数的a是:﹣1,1,3,5,
∴和为8,
故选:B.
4.(2021春?沙坪坝区校级月考)已知关于x的不等式组有解,且关于y的分式方程=4﹣有正整数解,则所有满足条件的整数a的值的个数为( )
A.2
B.3
C.4
D.5
【解答】解:
解不等式①得x<2,
解不等式②得x>﹣1,
∵不等式组有解,
∴﹣1<2,
解得a<9,
解分式方程=4﹣得y=,
∵方程的解为正数,
∴>0且≠3,
∴a>﹣且a≠3,
∴﹣<a<9且a≠3,
满足使方程的解为正整数的整数a的值有0,6两个.
故选:A.
5.(2021春?茅箭区月考)某施工队计划修建一个长为600米的隧道,第一周按原计划的速度修建,一周后以原来速度的1.5倍修建,结果比原计划提前一周完成任务,若设原计划一周修建隧道x米,则可列方程为( )
A.=+2
B.=﹣2
C.=+1
D.=﹣1
【解答】解:设原计划一周修建隧道x米,则提速后的速度为一周修建1.5x米,
根据题意,得:=+1.
故选:C.
6.(2021?铜梁区校级一模)若整数a使关于x的不等式组有且只有两个整数解,且关于y的分式方程﹣=﹣2的解为正数,则满足上述条件的a的和为( )
A.3
B.4
C.5
D.6
【解答】解:,
解不等式①得:x≤2,
解不等式②得:x≥,
∴不等式组的解集为≤x≤2,
∵不等式组有且只有两个整数解,
∴0<≤1,
∴0<a≤3;
分式方程两边都乘以(y﹣1)得:1﹣3y+2a=﹣2(y﹣1),
解得:y=2a﹣1,
∵分式方程的解为正数,
∴2a﹣1>0,
∴a>;
∵y﹣1≠0,
∴y≠1,
∴2a﹣1≠1,
∴a≠1,
∴<a≤3,且a≠1,
∵a是整数,
∴a=2或3,
∴2+3=5,
故选:C.
7.(2021?九龙坡区校级模拟)若数m使关于x的不等式组有解且至多有3个整数解,且使关于x的分式方程有整数解,则满足条件的所有整数m的个数是( )
A.5
B.4
C.3
D.2
【解答】解:,
解不等式①得:x≥﹣1,
∴﹣1≤x<,
∵不等式组有解且至多3个整数解,
∴﹣1<<2,
∴﹣3<m<6,
分式方程两边都乘以(x﹣1)得:mx﹣2﹣3=2(x﹣1),
∴(m﹣2)x=3,
当m≠2时,x=,
∵x﹣1≠0,
∴x≠1,
∴≠1,
∴m≠5,
∵方程有整数解,
∴m﹣2=±1,±3,
解得:m=3,1,5,﹣1,
∵m≠5,
∴,m=3,1,﹣1.
故选:C.
8.(2021春?重庆月考)若关于x的一元一次不等式组有且仅有3个整数解,且关于x的分式方程+=1有正数解,则所有满足条件的整数a的和为( )
A.12
B.13
C.14
D.15
【解答】解:,
解不等式①得:x<5,
解不等式②得:x≥,
∴不等式组的解集为,
∵不等式组有且仅有3个整数解,
∴1<≤2,
∴2<a≤6;
分式方程两边都乘以(x﹣1)得:ax﹣2﹣3=x﹣1,
解得:x=,
∵x﹣1≠0,
∴x≠1,
∵方程有正数解,
∴0,≠1,
∴a>1,a≠5,
∴2<a≤6,且a≠5,
∴a的整数解为3,4,6,和为13,
故选:B.
9.(2018春?温州期末)甲、乙、丙三名打字员承担一项打字任务,已知如下信息
如果每小时只安排1名打字员,那么按照甲、乙、丙的顺序至完成工作任务,共需( )
A.13小时
B.13小时
C.14小时
D.14小时
【解答】解:设甲单独完成任务需要x小时,则乙单独完成任务需要(x﹣5)小时,则
=.
解得x=20
经检验x=20是原方程的根,且符合题意.
则丙的工作效率是.
所以一轮的工作量为:++=.
所以4轮后剩余的工作量为:1﹣=.
所以还需要甲、乙分别工作1小时后,丙需要的工作量为:﹣﹣=.
所以丙还需要工作小时.
故一共需要的时间是:3×4+2+=14小时.
故选:C.
10.设x<0,x﹣=,则代数式的值( )
A.1
B.
C.
D.
【解答】解:∵x﹣=,
∴(x)2=5,
∴x2+=7,
∴(x+)2=x2+2+=9,
∵x<0,
∴x+=﹣3,
∴x2+1=﹣3x,
∴x4+1=7x2,
∵(x2+)2=x4+2+,
∴x4+=47,
∴x8+1=47x4,
∵x3+=(x+)(x2﹣1+),
∴x3+=﹣18,
∴x6+1=﹣18x3,
∴原式=
=
=
=
=
故选:B.
二.填空题(共10小题)
11.(2020秋?锦江区校级月考)若关于x的一元一次不等式组的解集为x≥5,且关于y的分式方程+=﹣1有非负整数解,则符合条件的所有整数a的和为 ﹣2 .
【解答】解:,
解不等式①得:x≥5,
解不等式②得:x>a+2,
∵解集为x≥5,
∴a+2<5,
∴a<3;
分式方程两边都乘以(y﹣2)得:y﹣a=﹣(y﹣2),
解得:y=,
∵分式方程有非负整数解,
∴≥0,
∴a≥﹣2,
∵≠2,
∴a≠2,
综上所述,﹣2≤a<3且a≠2,
∴符合条件的所有整数a的数有:﹣2,﹣1,0,1,
和为﹣2﹣1+0+1=﹣2.
故答案为:﹣2.
12.(2020秋?沙坪坝区校级月考)中秋、国庆“双节”前,某酒店推出甲,乙两种包装的月饼,其中甲种包装有五仁饼3个,莲蓉饼3个,豆沙饼2个,乙种包装有五仁饼1个,莲蓉饼1个,豆沙饼2个,每种包装每盒月饼的成本价为该盒中所有月饼的成本价之和.已知每个五仁饼与每个莲蓉饼的成本价之比为5:4,每盒乙包装月饼售价98元,利润率是40%,两种包装的月饼共50盒总价6123元,总利润率是30%.中秋节后,为降价促销,甲种包装每盒每类月饼各少装一个,乙种包装每盒少装月饼后售价降为原来的一半,利润率不变,那么这样包装的两种月饼共50盒的总成本是 4710 元(其中甲种包装少装月饼后的盒数与节前50盒中甲种包装月饼的盒数相同,当然乙种包装盒数也相同).
【解答】解:设乙的成本价为a,
根据题意列出90﹣s=40%a,
解得a=70,
设五仁饼的成本价为x,则一个莲蓉饼的成本价,则两豆沙饼成本价为(70﹣),
设甲礼盒和乙礼盒分别为m盒和n盒,m+n=50
则有70n+m(3x+3×)=6213÷(1+30%)
70n+70m+mx=4710.
xm=,
节后乙每盒成本98÷2÷(1+40%)=35,
甲每盒成本2x+2×x+35﹣x=35+x,
总成本35n+m(35+x)=35×50+×=2657.5.
故答案为:2657.5.
13.(2019?雨城区校级模拟)若数a使关于x的不等式组有且只有四个整数解,且使关于y的方程=2的解为非负数,则符合条件的所有整数a的和为 1 .
【解答】解:,
解①得,x<5;
解②得,
∴不等式组的解集为;
∵不等式有且只有四个整数解,
∴,
解得,﹣2<a≤2;
解分式方程得,y=2﹣a(a≠1);
∵方程的解为非负数,
∴2﹣a≥0即a≤2且a≠1
综上可知,﹣2<a≤2且a≠1,
∵a是整数,
∴a=﹣1,0,2;
∴﹣1+0+2=1,
故答案为:1.
14.(2014春?青羊区期末)已知x2﹣5x+1=0,则的值是 .
【解答】解:∵x2﹣5x+1=0,
∴x2=5x﹣1,
∴原式=
=
=
=
=
=.
故答案为:.
15.(2009春?营山县期末)已知,则= ﹣ .
【解答】解:∵﹣=2,
∴=2,即x﹣y=﹣2xy,
原式=
=
=
=﹣.
故答案为:﹣.
16.已知实数x,y,z,a满足x+a2=2010,y+a2=2011,z+a2=2012,且xyz=6,则代数式++﹣﹣﹣的值等于 .
【解答】解:∵xyz=6,
∴++﹣﹣﹣
=﹣
=﹣
=
=[(x﹣y)2+(y﹣z)2+(x﹣z)2],
∵x+a2=2010,y+a2=2011,z+a2=2012,
∴x﹣y=﹣1,y﹣z=﹣1,x﹣z=﹣2,
∴原式=×[(﹣1)2+(﹣1)2+(﹣2)2]=×(1+1+4)==,
故答案为:.
17.“非洲猪瘟”本是一种只在家畜之间传播的瘟疫,但最近已严重威胁到广大人民群众的生命安全,现我市有一组检疫工作人员(工作人员每人每天生猪检疫的效率相等),需对甲、乙两个生猪养殖场的所有生猪逐一检疫,已知,甲养殖场的生猪比乙养殖场的生猪多1倍.上午全部工作人员在甲养殖场检疫,为了尽快完成检疫,下午所有工作人员的平均工作效率提高了20%,但下午有一人因事离开,剩下的工作人员的一半仍留在甲养殖场(上、下午的工作时间相等),到下班前刚好把甲养殖场的生猪检疫完毕,另一半工作人员去乙养殖场检疫,到下班前还剩下一小部分生猪未检疫,最后由6人以提高前的检疫速度,再用不到半天的工作时间就完成了检疫.则这组工作人员最多有 27 人.
【解答】解:设每人每天可检疫x头猪,该组检疫工作人员有y人,由题意得:
xy+x(1+20%)×<2[x(1+20%)×+6×],
化简得:0.4y<11.4
∴y<28.5,
∵y只能为正整数,且有一人离开后,人数平分
∴y的最大值为27.
故答案为:27.
18.(2021?九龙坡区模拟)临近端午,甲、乙两生产商分别承接制作白粽,豆沙粽和蛋黄粽的任务(三种粽子都有成品,甲生产商安排200名工人制作白粽和豆沙粽,每人只能制作其中一种粽子,乙生产商安排100名工人制作蛋黄粽,其中豆沙粽的人均制作数量比白粽的人均制作数量少15个,蛋黄粽的人均制作数量比豆沙粽的人均制作数量少20%,若本次制作的白粽、豆沙粽和蛋黄粽三种粽子的人均制作数量比白粽的人均制作数用少20%,且豆沙粽的人均制作量为偶数个,则本次可制作的粽子数量最多为 23760 个.
【解答】解:设生产豆沙粽的有x人,白粽子的有(200﹣x)人;生产豆沙粽人均y个,白粽子人均(y+15)个,则蛋黄粽子人均y(1﹣20%)=0.8y个.
由题意得[xy+(y+15)(200﹣x)+100×0.8y]×=(y+15)×(1﹣20%),
∴(xy+200y+3000﹣xy﹣15x+80y)×=0.8y+12,
∴y+10﹣x=0.8y+12,
∴y﹣x=2,
∴x=y﹣40.
又∵200﹣x>0,y>0,
∴0<y<90.
∵需要制作的粽子最多,而粽子总数为300(0.8y+12),y是偶数
∴y=84时,x=184,制作的粽子最多为23760.
故答案为:23760.
19.(2020秋?北京期末)依据如图流程图计算﹣,需要经历的路径是 ② (只填写序号),输出的运算结果是 .
【解答】解:∵两个分式分母不同,
∴经历路径为②.
根据路径②计算如下:
原式=,
=﹣,
=,
故答案为:②,.
20.设2016a3=2017b3=2018c3,abc>0,且=++,则++= 1
【解答】解:===(),
++=+=(),
即:=,解得:=1.
故答案为1.
三.解答题(共10小题)
21.(2021?包河区三模)市政府为美化城市环境,计划在某区城种植树木2000棵,由于青年志愿者的加入,实际每天植树棵数是原计划的2倍,结果提前4天完成任务.求实际每天植树多少棵?
【解答】解:设原计划每天植树x棵,则实际每天植树棵数是2x棵,
根据题意,得﹣=4.
解得x=250.
经检验x=250是原方程的解,且符合题意.
所以2x=500.
答:实际每天植树500棵.
22.(2021?平房区三模)某体育用品商店计划购进一些篮球和排球.已知每个篮球的进价和每个排球的进价的和为200元,用2400元购进的篮球数量是用800元购进排球数量的2倍.
(1)求每个篮球和每个排球的进价各是多少元;
(2)若该体育用品商店计划购进篮球和排球共40个,且购进的总费用不超过3800元,则该体育用品商店最多可以购进篮球多少个?
【解答】解:(1)设每个篮球的进价为x元,则每个排球的进价为(200﹣x)元.
根据题意得.
解得x=120.
经检验x=120是原分式方程的解.
∴200﹣x=200﹣120=80(元).
答:每个篮球的进价为120元,每个排球的进价为80元.
(2)设该体育用品商店可以购进篮球a个,则购进排球(40﹣a)个,
根据题意,得120a+80(40﹣a)≤3800.
解得a≤15.
答:该体育用品商店最多可以购进篮球15个.
23.(2021?岳阳二模)岳阳市区某中学为了创建“书香校园”,今年春季购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元,已知学校用20000元购买的科普类图书的本数与用15000元购买的文学类图书的本数相等.
(1)求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
(2)学校计划在五月份再添置600本这两类图书,且费用不超过10000元,问最多可以购买科普类图书多少本?
【解答】解:(1)设科普类书的单价为x元/本,则文学类书的单价为(x﹣5)元/本,
依题意:,
解之得:x=20.
经检验,x=20是所列分程的根,且合实际,
∴x﹣5=15.
答:科普类书单价为20元/本,文学类书单价为15元/本;
(2)设科普类书购a本,则文学类书购(600﹣a)本,
依题意:20a+15(600﹣a)≤10000,
解之得:a≤200.
答:最多可购科普类图书200本.
24.(2021?宝安区模拟)为了抗击“新型肺炎”,我市某医药器械厂接受了生产一批高质量医用口罩的任务,任务要求在30天之内(含30天)生产A型和B型两种型号的口罩共200万只.在实际生产中,由于受条件限制,该工厂每天只能生产一种型号的口罩.已知该工厂每天可生产A型口罩的个数是生产B型口罩的2倍,并且加工生产40万只A型口罩比加工生产50万只B型口罩少用6天.
(1)该工厂每天可加工生产多少万只B型口罩?
(2)若生产一只A型口罩的利润是0.8元,生产一只B型口罩的利润是1.2元,在确保准时交付的情况下,如何安排工厂生产可以使生产这批口罩的利润最大?
【解答】解:(1)设工厂每天可加工生产x万只B型口罩,则
.
解得x=5.
经检验x=5是原方程的根.
答:该工厂每天可生产5万只B型口罩.
(2)设安排工厂生产A型口罩a万只,则生产B型口罩(200﹣a)万只,这批口罩的总利润为W万元,则有:
W=0.8a+1.2(200﹣a)=﹣0.4a+240.
∵要确保准时交付,
∴.
∵k=﹣0.4<0,W随a的增大而减小,
∴当a=100时,W最大=200万元.
答:应该安排该工厂生产100万只A型口罩,100万只B型口罩时利润最大.
25.(2020秋?香洲区期末)已知(x+a)(x+b)=x2+mx+n.
(1)若a=﹣3,b=2,则m= ﹣1 ,n= ﹣6 ;
(2)若m=﹣2,,求的值;
(3)若n=﹣1,当时,求m的值.
【解答】解:(1)将a=﹣3,b=2代入(x+a)(x+b)得:
(x+a)(x+b)=(x﹣3)(x+2)=x2﹣x﹣6=x2+mx+n,
∴m=﹣1,n=﹣6.
故答案为:﹣1,﹣6.
(2)∵(x+a)(x+b)=x2+(a+b)x+ab=x2+mx+n.
∴,
∴+====﹣4.
(3)∵a+b=m,ab=n=﹣1,,
∴,
∴,
∴,
∴m2﹣2×(﹣1)+4m+2=0,
∴m2+4m+4=0,
∴(m+2)2=0,
∴m=﹣2.
26.(2021春?滨湖区期中)小红、小刚、小明三位同学在讨论:当x取何整数时,分式的值是整数?
小红说:这个分式的分子、分母都含有x,它们的值均随x取值的变化而变化,有点难.
小刚说:我会解这类问题:当x取何整数时,分式的值是整数?3是x+1的整数倍即可,注意不要忘记负数哦.
小明说:可将分式与分数进行类比.本题可以类比小学里学过的“假分数”,当分子大于分母时,可以将“假分数”化为一个整数与“真分数”的和.比如:==2+(通常写成带分数:2).类比分式,当分子的次数大于或等于分母次数时,可称这样的分式为“假分式”,若将化成一个整式与一个“真分式”的和,就转化成小刚说的那类问题了!
小红、小刚说:对!我们试试看!…
(1)解决小刚提出的问题;
(2)解决他们共同讨论的问题.
【解答】解:(1)当x+1=±1,±3时,分式的值是整数,
∴x=0,﹣2,2,﹣4.
(2)=3﹣,
当x+1=±1,±5时,分式的值为整数,
∴x=0,﹣2,4,﹣6.
27.(2021春?大兴区期中)已知非零实数a、b满足等式,求的值.
【解答】解:等式两边都乘以ab得:b2+a2+5=4a+2b,
整理得:(b﹣1)2+(a﹣2)2=0,
∴a=2,b=1,
代入得:
原式=.
28.(2020秋?连山区期末)阅读下面的材料,并解答后面的问题
材料:将分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式.
解:由分母为x+1,可设3x2+4x﹣1=(x+1)(3x+a)+b.
因为(x+1)(3x+a)+b=3x2+ax+3x+a+b=3x2+(a+3)x+a+b,
所以3x2+4x﹣1=3x2+(a+3)x+a+b.
所以,解得.
所以==﹣=3x+1﹣.
这样,分式就被拆分成了一个整式3x+1与一个分式的差的形式.
根据你的理解解决下列问题:
(1)请将分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式;
(2)若分式拆分成一个整式与一个分式(分子为整数)的和(差)的形式为:5m﹣11+,求m2+n2+mn的最小值.
【解答】解:(1)由分母为x﹣1,可设2x2+3x+6=(x﹣1)(2x+a)+b.
因为(x﹣1)(2x+a)+b=2x2+ax﹣2x﹣a+b=2x2+(a﹣2)x﹣a+b,
所以2x2+3x+6=2x2+(a﹣2)x﹣a+b,
因此有,
解得,
所以==2x+5+;
(2)由分母为x+2,可设5x2+9x﹣3=(x+2)(5x+a)+b,
因为(x+2)(5x+a)+b=5x2+ax+10x+2a+b=5x2+(a+10)x+2a+b,
所以5x2+9x﹣3=5x2+(a+10)x+2a+b,
因此有,
解得,
所以==5x﹣1﹣,
所以5m﹣11+=5x﹣1﹣,
因此5m﹣11=5x﹣1,n﹣6=﹣x﹣2,
所以m=x+2,n=﹣x+4,
所以m2+n2+mn=x2﹣2x+28=(x﹣1)2+27,
因为(x﹣1)2≥0,所以(x﹣1)2+27≥27,
所以m2+n2+mn的最小值为27.
29.(2020秋?乌苏市期末)近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路商业运营树立了新的标杆.随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,跑出发展新速度,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从A地到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为多少千米?
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
【解答】解:(1)普通列车的行驶路程为:400×1.3=520(千米);
(2)设普通列车的平均速度为x千米/时,则高铁的平均速度为2.5千米/时,则题意得:
=﹣3,
解得:x=120,
经检验x=120是原方程的解,
则高铁的平均速度是120×2.5=300(千米/时),
答:普通列车的平均速度是120千米/时,高铁的平均速度是300千米/时.
30.(2021?禅城区校级一模)先化简(1﹣)÷,再从0,2,﹣1,1中选择一个合适的数代入并求值.
【解答】解:原式=×=.
因为x不能取±1,2,
所以把x=0代入,原式==﹣.
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
