第一章 三角形的证明 专题复习(含解析)
文档属性
| 名称 | 第一章 三角形的证明 专题复习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1015.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 17:03:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大新版专题复习《三角形的证明》
一.选择题(共10小题)
1.(2021春?江都区校级期末)等腰三角形的面积为24平方厘米,腰长8厘米.在底边上有一个动点P,则P到两腰的距离之和为( )
A.4cm
B.6cm
C.8cm
D.10cm
2.(2021?南山区校级二模)下列命题中真命题是( )
A.的算术平方根是3
B.数据a+2,a,a+3,a+2,a+3与2,0,3,2,3的方差相同
C.正六边形的内角和为360°
D.对角线相等的四边形是矩形
3.(2021春?武汉期中)已知等边三角形的边长为4,则其面积为( )平方单位.
A.4
B.8
C.12
D.16
4.(2021春?沙坪坝区期中)在△ABC中,∠A:∠B:∠C=2:5:3,则△ABC的形状是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
5.(2021?坪山区二模)如图,在△ABC中,∠B=90°,C是BD上一点,BC=10,∠ADB=45°,∠ACB=60°,则CD长为( )
A.10﹣
B.10﹣10
C.10﹣3
D.10﹣10
6.(2021春?汉寿县期中)如图,四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是( )
A.1
B.2
C.3
D.4
7.(2021?滨湖区一模)如图所示,在等边三角形ABC中,BC=6,E是中线AD上一点,现有一动点P沿着折线A﹣E﹣C运动,在AE上的速度是4单位/秒,在CE上的速度是2单位/秒,则点P从A运动到C所用时间最少时,AE长为( )
A.3
B.
C.
D.2
8.(2021?蜀山区一模)如图,在△ABC中,AB=AD,E为BD中点,连接AE,∠BAD=∠CAE,若BD=CD=6,则AB的长为( )
A.6
B.3
C.
D.
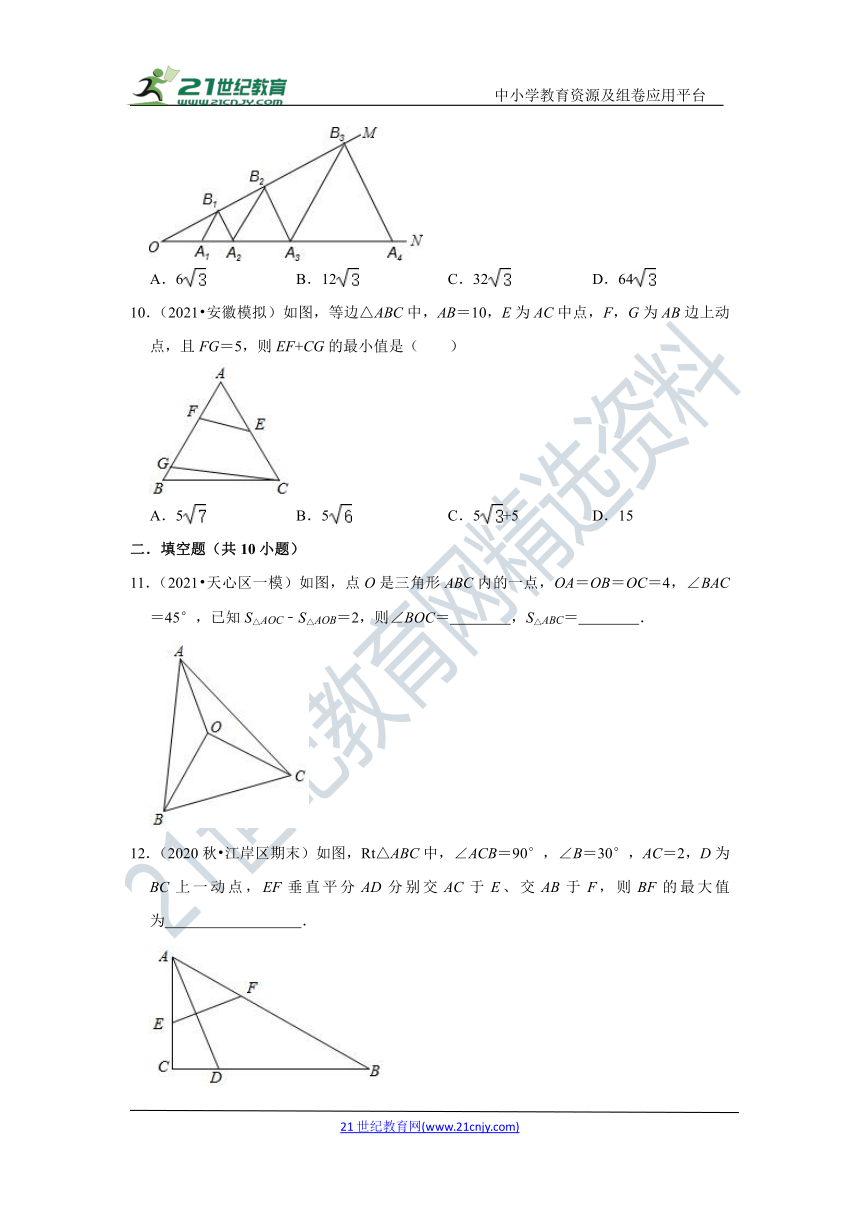
9.(2020秋?承德县期末)如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )
A.6
B.12
C.32
D.64
10.(2021?安徽模拟)如图,等边△ABC中,AB=10,E为AC中点,F,G为AB边上动点,且FG=5,则EF+CG的最小值是( )
A.5
B.5
C.5+5
D.15
二.填空题(共10小题)
11.(2021?天心区一模)如图,点O是三角形ABC内的一点,OA=OB=OC=4,∠BAC=45°,已知S△AOC﹣S△AOB=2,则∠BOC=
,S△ABC=
.
12.(2020秋?江岸区期末)如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,D为BC上一动点,EF垂直平分AD分别交AC于E、交AB于F,则BF的最大值为
.
13.(2021?巩义市模拟)点P是等边三角形ABC内部一点,过点P作三边的垂线,分别记为PH1,PH2,PH3,设△ABC的边长为a.若PH1=1,PH2=3,PH3=5,则a=
;若a=2,则PH1+PH2+PH3=
.
14.(2021春?金牛区校级期中)已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边△ABC的内部时,那么∠BOC和∠BPC的数量关系是:∠BOC=
.
15.(2020?皇姑区校级模拟)在平面直角坐标系中,A(0,3)、B(,0)、Q(0,),C是x轴上一点,以AC为边向右侧作正△ACD,P为AD的中点.当C从O运动到B点时,PQ的最小值为
.
16.(2020春?新都区期末)边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点顺次连接,又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图)…,按此方式依次操作,则第7个正六边形的边长是
.
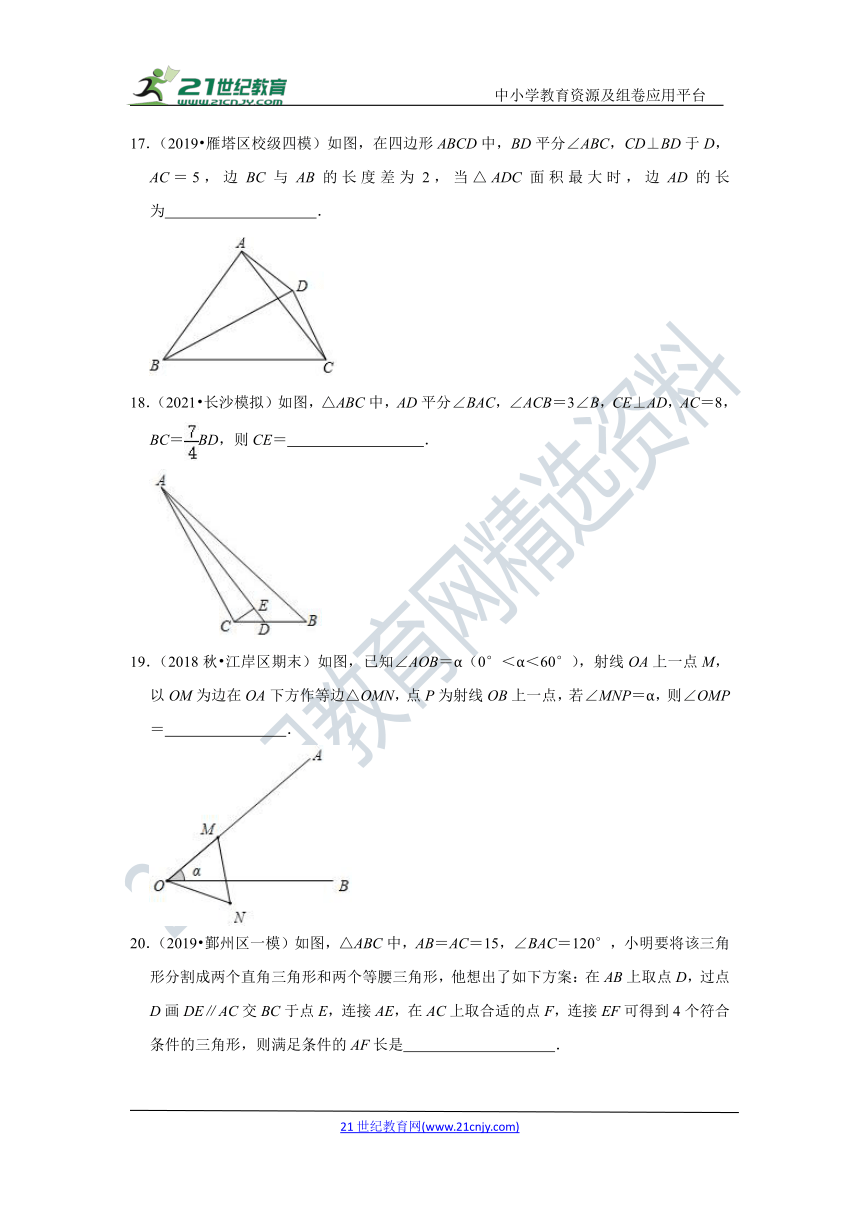
17.(2019?雁塔区校级四模)如图,在四边形ABCD中,BD平分∠ABC,CD⊥BD于D,AC=5,边BC与AB的长度差为2,当△ADC面积最大时,边AD的长为
.
18.(2021?长沙模拟)如图,△ABC中,AD平分∠BAC,∠ACB=3∠B,CE⊥AD,AC=8,BC=BD,则CE=
.
19.(2018秋?江岸区期末)如图,已知∠AOB=α(0°<α<60°),射线OA上一点M,以OM为边在OA下方作等边△OMN,点P为射线OB上一点,若∠MNP=α,则∠OMP=
.
20.(2019?鄞州区一模)如图,△ABC中,AB=AC=15,∠BAC=120°,小明要将该三角形分割成两个直角三角形和两个等腰三角形,他想出了如下方案:在AB上取点D,过点D画DE∥AC交BC于点E,连接AE,在AC上取合适的点F,连接EF可得到4个符合条件的三角形,则满足条件的AF长是
.
三.解答题(共10小题)
21.(2021?蔡甸区二模)如图,△ABC中,点D在BC边上,且∠ADB=90°∠CAD.
(1)求证:AD=AC;
(2)点E在AB边上,连接CE交AD于点F,且∠CFD=∠CAB,AE=BD,
①求∠ABC的度数;
②若AB=8,DF=2AF,直接写出EF的长.
22.(2021春?中原区校级月考)如图,在△ABC中,DM,EN分别垂直平分边AC和边BC,交边AB于M,N两点,DM与EN相交于点F.
(1)若AB=3cm,求△CMN的周长.
(2)若∠MFN=70°,求∠MCN的度数.
23.(2020秋?潮州期末)如图,在等边三角形ABC中,D是AB上的一点,E是CB延长线上一点,连接CD、DE,已知∠EDB=∠ACD.
(1)求证:△DEC是等腰三角形.
(2)当∠BDC=5∠EDB,EC=8时,求△EDC的面积.
24.(2021?西城区校级模拟)(1)小My同学在网络直播课中学习了勾股定理,他想把这一知识应用在等边三角形中:边长为a的等边三角形面积是
(用含a的代数式表示);
(2)小My同学进一步思考:是否可以将正方形剪拼成一个等边三角形(不重叠、无缝隙)?
①如果将一个边长为2的正方形纸片剪拼等边三角形,那么该三角形边长的平方是
;
②小My同学按下图切割方法将正方形ABCD剪拼成一个等边三角形EFG:M、N分别为AB、CD边上的中点,P、Q是边BC、AD上两点,G为MQ上一点,且∠MGP=∠PGN=∠NGQ=60°.
请补全图形,画出拼成正三角形的各部分分割线,并标号;
③正方形ABCD的边长为2,设BP=x,则x2=
.
25.(2020秋?五常市期末)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.
(1)求证:AB=AC;
(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.
26.(2020秋?临沭县期末)如图,在△ABC中,AB=AC,AD=DE=EB,BD=BC,试求∠A的度数.
27.(2020春?东明县期末)如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.
(1)求证:DF是线段AB的垂直平分线;
(2)当AB=AC,∠A=46°时,求∠EBC及∠F的度数.
28.(2019秋?巩义市期末)如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts.
(1)用含t的式子表示线段AP、AQ的长;
(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?
(3)当t为何值时,PQ∥BC?
29.(2020秋?朝阳期中)在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD=
;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC=
.
30.(2020春?揭西县期末)如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
北师大新版数学专题复习《三角形的证明》
参考答案与试题解析
一.选择题(共10小题)
1.(2021春?江都区校级期末)等腰三角形的面积为24平方厘米,腰长8厘米.在底边上有一个动点P,则P到两腰的距离之和为( )
A.4cm
B.6cm
C.8cm
D.10cm
【解答】解:已知:△ABC中,PE⊥AB于E,PF⊥AC于F,AB=AC=8厘米,△ABC的面积为24平方厘米,P是底边BC上一个动点.
求:PE+PF的值.
解:连接AP,
∵PE⊥AB,PF⊥AC,
∴S△ABP=AB?PE,S△ACP=AC?PF,
∵S△ABP+S△ACP=S△ABC,S△ABC=24,
∴AB?PE+AC?PF=24,
∴AB(PE+PF)=24,
∴PE+PF==6cm,
故选:B.
2.(2021?南山区校级二模)下列命题中真命题是( )
A.的算术平方根是3
B.数据a+2,a,a+3,a+2,a+3与2,0,3,2,3的方差相同
C.正六边形的内角和为360°
D.对角线相等的四边形是矩形
【解答】解:A、的算术平方根是,本选项错误,不符合题意.
B、数据a+2,a,a+3,a+2,a+3与2,0,3,2,3的方差相同,正确,本选项符合题意.
C、正六边形的内角和为360°,错误,应该是720°,本选项不符合题意.
D、对角线相等的四边形是矩形,错误,应该是对角线相等的平行四边形是矩形,本选项不符合题意.
故选:B.
3.(2021春?武汉期中)已知等边三角形的边长为4,则其面积为( )平方单位.
A.4
B.8
C.12
D.16
【解答】解:如图,等边三角形ABC,AB=BC=4,
作AD⊥BC,垂足为D,
∴BD=CD=2,
在Rt△ABD中,AD=,
∴S△ABC=BC?AD
=×4×
=,
故选:A.
4.(2021春?沙坪坝区期中)在△ABC中,∠A:∠B:∠C=2:5:3,则△ABC的形状是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
【解答】解:设∠A=2x°,∠B=5x°,∠C=3x°,
∵∠A+∠B+∠C=180°,
∴2x+5x+3x=180,
解得:x=18,
∴∠B=5x°=90°,
∴△ABC是直角三角形,
故选:B.
5.(2021?坪山区二模)如图,在△ABC中,∠B=90°,C是BD上一点,BC=10,∠ADB=45°,∠ACB=60°,则CD长为( )
A.10﹣
B.10﹣10
C.10﹣3
D.10﹣10
【解答】解:∵在△ABC中,∠B=90°,∠ACB=60°,
∴∠CAB=30°,
∴BC=AC,
∴AC=2BC=20,
∴AB==10,
∵∠ADB=45°,
∴∠DAB=45°,
∴∠DAB=∠ADB,
∴BD=AB=10,
∴CD=BD﹣BC=10﹣10,
故选:B.
6.(2021春?汉寿县期中)如图,四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是( )
A.1
B.2
C.3
D.4
【解答】解:∵BD⊥CD,∠A=90°
∴∠ABD+∠ADB=90°,
∠CBD+∠C=90°,
∴∠ABD=∠CBD,
由垂线段最短得,DP⊥BC时DP最小,
此时,DP=AD=3.
故选:C.
7.(2021?滨湖区一模)如图所示,在等边三角形ABC中,BC=6,E是中线AD上一点,现有一动点P沿着折线A﹣E﹣C运动,在AE上的速度是4单位/秒,在CE上的速度是2单位/秒,则点P从A运动到C所用时间最少时,AE长为( )
A.3
B.
C.
D.2
【解答】解:作CM⊥AB于点M,点P在A﹣E﹣C上运动时间为+,=(),
∵∠BAD=30°,
∴EM=AE,
∴()=(EM+CE),
当C,E,M共线时,点P运动时间最短,
∴CM为三角形中线,点E为重心,
∵∠CAD=30°,CD=BC=3,
∴AD=CD=3,
AE=AD=2.
故选:D.
8.(2021?蜀山区一模)如图,在△ABC中,AB=AD,E为BD中点,连接AE,∠BAD=∠CAE,若BD=CD=6,则AB的长为( )
A.6
B.3
C.
D.
【解答】解:过点D作DF⊥AC于F,如图:
∵AB=AD,E为BD中点,
∴AE⊥BD,∠BAE=∠DAE.
∵BD=CD=6,
∴BE=DE=3,CD=4.
∵∠BAD=∠CAE,
∴∠BAE=∠DAE=∠DAF,
∴DF=DE=3,FC==.
∵∠CFD=∠AEC=90°,∠C=∠C,
∴△CFD∽△CEA,即,AE=3.
∴AB===6.
故选:A.
9.(2020秋?承德县期末)如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )
A.6
B.12
C.32
D.64
【解答】解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2=2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:A7B7=26B1A2=26=64,B6A7==32,△B7B6A7是直角三角形,∠B7B6A7=90°,
∴B6B7===32.
故选:C.
10.(2021?安徽模拟)如图,等边△ABC中,AB=10,E为AC中点,F,G为AB边上动点,且FG=5,则EF+CG的最小值是( )
A.5
B.5
C.5+5
D.15
【解答】解:如图:
作C点关于AB的对称点C′,
则C'G=CG,
取BC的中点Q,
连接EQ,GQ,
∵点E是AC的中点,
∴EQ=AB=5=FG,EQ∥AB,
∴四边形EFGQ是平行四边形,
∴EF=GQ,
∴当点C',G,Q在同一条线上时,CG+EF最小,
作C′H⊥BC交BC的延长线于点H,
∵BC=BC′=10,∠CBC′=120°,
∴HC′=5,HB=5,
∴HQ=10,
∴C′Q==5,
∴EF+CG的最小值是5.
故选:A.
二.填空题(共10小题)
11.(2021?天心区一模)如图,点O是三角形ABC内的一点,OA=OB=OC=4,∠BAC=45°,已知S△AOC﹣S△AOB=2,则∠BOC= 90° ,S△ABC= 8+2 .
【解答】解:∵OA=OB=OC=4,
∴△ABC是以O为圆心,半径为4的内接三角形,
延长AO交BC于点E,作BM⊥AE,CN⊥AE,
∵∠BAC=45°,
∴∠BOC=2∠BAC=90°,
∴BC=OB=4,
∵S△AOC﹣S△AOB=2,
∴AO?CN﹣AO?BM=2(CN﹣BM)=2,
∴CN﹣BM=1.
∵∠BOM+∠CON=90°,∠BOM+∠OBM=90°,
∴∠CON=∠OBM,
又∵∠BMO=∠CNO=90°,OB=OC,
在△BOM和△CON中,
∴△BOM≌△CON(AAS),
∴OM=CN,
在Rt△BOM和Rt△CON中,由勾股定理得:
BM2+OM2=ON2+CN2=16,
即BM2+CN2=16,
联立方程,
解得BM=或BM=(舍).
∴CN=BM+1=.
∴S△AOC+S△AOB=AO?CN+AO?BM=2(CN+BM)=2.
∵S△BOC=OB?OC=8,
∴S△ABC=S△AOC+S△AOB+S△BOC=8+2.
故答案为:90°,8+2.
12.(2020秋?江岸区期末)如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,D为BC上一动点,EF垂直平分AD分别交AC于E、交AB于F,则BF的最大值为 .
【解答】解:∵Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,
∴AB=2AC=4,
∵EF垂直平分AD,
∴AF=DF,
若要使BF最大,则AF需要最小,
∴以F为圆心,AF为半径的圆与BC相切即可,
∴FD⊥BD,
∴AB=AF+2AF=4,
∴AF=,
∴BF的最大值为4﹣=,
故答案为:.
【点评】本题主要考查了线段垂直平分线的性质、30°角所对直角边是斜边的一半以及圆与直线的位置关系,将BF的最大值转化为AF最小是解决本题的关键,属于压轴题.
13.(2021?巩义市模拟)点P是等边三角形ABC内部一点,过点P作三边的垂线,分别记为PH1,PH2,PH3,设△ABC的边长为a.若PH1=1,PH2=3,PH3=5,则a= 6 ;若a=2,则PH1+PH2+PH3= 3 .
【解答】解:连结PA,PB,PC,设△ABC的BC边上的高为h,则h=AB?sin60°=a,
∴S△ABC==×a×a=a2,
∵S△ABC=S△ABP+S△BCP+S△ACP,
∴a2=,
解得a=6;
当a=2时,
∵S△ABC=S△ABP+S△BCP+S△ACP,
∴×(2)2=×++,
∴PH1+PH2+PH3=3.
故答案为:6;3.
【点评】本题考查了等边三角形的性质,利用等面积法列出方程是解题的关键.
14.(2021春?金牛区校级期中)已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边△ABC的内部时,那么∠BOC和∠BPC的数量关系是:∠BOC= 4∠BPC﹣360° .
【解答】解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(
∠ABC+∠ACB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC,
即∠BAC=2∠BPC﹣180°;
如图,连接AO.
∵点O是这个三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,
∴∠BOC=360°﹣(∠AOB+∠AOC)
=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC
=2(2∠BPC﹣180°)
=4∠BPC﹣360°,
故答案为:4∠BPC﹣360°.
15.(2020?皇姑区校级模拟)在平面直角坐标系中,A(0,3)、B(,0)、Q(0,),C是x轴上一点,以AC为边向右侧作正△ACD,P为AD的中点.当C从O运动到B点时,PQ的最小值为 .
【解答】解:如图,连接OP,CP,
∵正△ACD中,P为AD的中点,
∴∠AOB=∠APC=90°,
∴O、A、P、C四点共圆,
∴∠AOP=∠ACP=30°,
∴当PQ⊥OP时,PQ最小,
即PQ的最小值为OQ=×=.
故答案为:.
16.(2020春?新都区期末)边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点顺次连接,又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图)…,按此方式依次操作,则第7个正六边形的边长是 ×()6a .
【解答】解:如图1,连接AD、DF、DB.
∵六边形ABCDEF是正六边形,
∴∠ABC=∠BAF=∠AFE,AB=AF,∠E=∠C=120°,EF=DE=BC=CD,
∴∠EFD=∠EDF=∠CBD=∠BDC=30°,
∵∠AFE=∠ABC=120°,
∴∠AFD=∠ABD=90°,
在Rt△ABD和RtAFD中,
∵,
∴Rt△ABD≌Rt△AFD(HL),
∴∠BAD=∠FAD=×120°=60°,
∴∠FAD+∠AFE=60°+120°=180°,
∴AD∥EF,
∵G、I分别为AF、DE中点,
∴GI∥EF∥AD,
∴∠FGI=∠FAD=60°,
∵六边形ABCDEF是正六边形,△QKM是等边三角形,
∴∠EDM=60°=∠M,
∴ED=EM,
同理AF=QF,
即AF=QF=EF=EM,
∵等边三角形QKM的边长是a,
∴第一个正六边形ABCDEF的边长是a,即等边三角形QKM的边长的,
如图2,过F作FZ⊥GI于Z,过E作EN⊥GI于N,
则FZ∥EN,
∵EF∥GI,
∴四边形FZNE是平行四边形,
∴EF=ZN=a,
∵GF=AF=×a=a,∠FGI=60°(已证),
∴∠GFZ=30°,
∴GZ=GF=a,
同理IN=a,
∴GI=a+a+a=a,即第二个等边三角形的边长是a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是×a;
同理第三个等边三角形的边长是×a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是××a;
同理第四个等边三角形的边长是()3a,第四个正六边形的边长是×()3a;
第五个等边三角形的边长是()4a,第五个正六边形的边长是×()4a;
…
第n个正六边形的边长是×()n﹣1a,
∴第七个正六边形的边长是×()6a.
故答案为:×()6a.
17.(2019?雁塔区校级四模)如图,在四边形ABCD中,BD平分∠ABC,CD⊥BD于D,AC=5,边BC与AB的长度差为2,当△ADC面积最大时,边AD的长为 .
【解答】解:延长CD与BA交于点E,
∵BD平分∠ABC,CD⊥BD于D,
∴△CAE为等腰三角形,D为CE中点,
∴S△ADC=S△ACE=S△ADE.
∵BC﹣AB=2,
∴AE=2,
当AE⊥AC时,△AEC面积最大,
∴此时△ADC面积最大.
∵CE===,
∴AD=CE=.
故答案为:.
18.(2021?长沙模拟)如图,△ABC中,AD平分∠BAC,∠ACB=3∠B,CE⊥AD,AC=8,BC=BD,则CE= .
【解答】解:延长CE交AB于F,过点D作DH⊥AB于H,DN⊥AC于N,过点A作AM⊥BC于M,如图所示:
∵CE⊥AD,
∴∠AEF=∠AEC=90°,
∵AD平分∠BAC,
∴∠FAE=∠CAE,DH=DN,
在△AEF与△AEC中,,
∴△AEF≌△AEC(ASA),
∴AF=AC=8,∠AFE=∠ACE,EF=CE,
∵∠AFC=∠B+∠ECD,
∴∠ACF=∠B+∠ECD,
∴∠ACB=2∠ECD+∠B,
∵∠ACB=3∠B,
∴2∠ECD+∠B=3∠B,
∴∠B=∠ECD,
∴CF=BF,
∵BC=BD,
∴=,
S△ADB=DH?AB=AM?BD,S△ACD=DN?AC=AM?CD,
∴=,
即==,
∴AB=AC=,
∴CF=BF=﹣8=,
∴CE=CF=,
故答案为:.
19.(2018秋?江岸区期末)如图,已知∠AOB=α(0°<α<60°),射线OA上一点M,以OM为边在OA下方作等边△OMN,点P为射线OB上一点,若∠MNP=α,则∠OMP= 30°或120°﹣α. .
【解答】解:(1)当P位于MN左侧时,如图1,
∵△OMN是等边三角形,
∴MN=MO=ON,∠MON=∠MNO=60°,
∵∠MNP=∠AOB=α,
∴∠PON=∠PNO,
∴PO=PN,
△MPO≌△MPN,(SAS)
∴∠OMP=∠NMP=∠OMN=×60°=30°
(2)当P位于MN右侧时,如图2,将△MNP绕着点M顺时针旋转60°得到△MOQ,
此时△MPQ是等边三角形,
∴∠MPQ=60°,
∴∠OMP=180°﹣∠MPQ﹣∠MOP=180°﹣60°﹣α=120°﹣α,
故答案为:30°或120°﹣α.
20.(2019?鄞州区一模)如图,△ABC中,AB=AC=15,∠BAC=120°,小明要将该三角形分割成两个直角三角形和两个等腰三角形,他想出了如下方案:在AB上取点D,过点D画DE∥AC交BC于点E,连接AE,在AC上取合适的点F,连接EF可得到4个符合条件的三角形,则满足条件的AF长是 5、10或 .
【解答】解:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE∥AC,
∴∠DEB=∠C=30°,∠BDE=120°,
∴△BDE是等腰三角形,∠ADE=180°﹣∠BDE=60°.
被分割的四个三角形中有两个直角三角形和两个等腰三角形.
①当∠AED=90°时,如图1:
∴∠DAE=180°﹣∠AED﹣∠ADE=30°,
∴∠EAF=∠BAC﹣∠DAE=90°.
则△EFC是等腰三角形.
∵∠AEC=180°﹣∠BED﹣∠DEA=60°,
∴△EFC是等腰三角形只可能存在∠FEC=∠C=30°的情况,
设AF=x,
∵∠AEF=180°﹣∠BED﹣∠AED﹣∠FEC=30°,
∴EF=2x,
∵EF=FC=2x,
∴AF+FC=3x=AC=15,
∴AF=5.
②当∠DAE=90°且∠AEF=90°时,如图2:
此时∠EAF=∠BAC﹣∠DAE=30°,
∴∠AFE=180°﹣∠AEF﹣∠EAF=60°
设AF=x,则EF=x,
∵∠EFC=180°﹣∠AFE=120°,
又∵∠FEC=180°﹣∠C﹣∠EFC=30°,
∴△EFC是等腰三角形,CF=EF=x,
∵AC=AF+FC=x+x=15,
∴AF=x=10.
③当∠DAE=90°且∠FEC=90°时,如图3.
∠FAE=∠BAC﹣∠DAE=30°,
∵∠AED=180°﹣∠DAE﹣∠ADE=30°,
∴∠AEF=180°﹣∠BED﹣∠FEC﹣∠AED=30°.
∴AF=AE,
设AF=EF=x,
∵∠FEC=90°,∠C=30°,
∴CF=2x,
∵AF+FC=x+2x=3x=AC=15,
∴AF=x=5.
④当∠AFE=∠EFC=90°时,则△ADE是等腰三角形,如图4
∵∠ADE=60°,
∴∠DAE=∠AED=60°,
∵∠EAF=∠BAC﹣∠DAE=60°,
∴∠AEF=180°﹣∠EAF﹣∠AFE=30°.
设AF=x,则EF=x.
∵∠EFC=90°,∠C=30°,
∴FC=EF=3x,
∵AC=AF+FC=x+3x=4x=15,
∴AF=.
故答案为:5、10或
三.解答题(共10小题)
21.(2021?蔡甸区二模)如图,△ABC中,点D在BC边上,且∠ADB=90°∠CAD.
(1)求证:AD=AC;
(2)点E在AB边上,连接CE交AD于点F,且∠CFD=∠CAB,AE=BD,
①求∠ABC的度数;
②若AB=8,DF=2AF,直接写出EF的长.
【解答】解:(1)∵∠ADB=∠ACB+∠CAD,∠ADB=90°∠CAD,
∴∠ACB=∠ADB﹣∠CAD=90°∠CAD,
∵∠ADB+∠CDA=180°,
∴∠CDA=180°﹣∠ADB=180°﹣(90°∠CAD)=90°∠CAD,
∴∠ACB=∠ADC,
∴AD=AC;
(2)①过点D作DG∥CE交AB于点G,
∵∠CFD=∠CAB,∠CFD=∠CAD+∠ACE,∠CAB=∠CAD+∠DAB,
∴∠ACE=∠DAB,
又∵∠ACD=∠ADC,∠ECB=∠ACD﹣∠ACE,∠B=∠ADC﹣∠DAB,
∴∠ECB=∠B,
∴CE=BE,
∵DG∥CE,
∴∠ECB=∠BDG,
∴∠BDG=∠B,
∴DG=BG,
∵∠AEC=∠DGA,AC=DA,∠ACE=∠DAG,
∴△AEC≌△DGA(AAS),
∴DG=AE,
又∵AE=BD,
∴DG=BD=BG,
∴△BDG为等边三角形,
∴∠ABC=60°;
②EF=.
过点D作DH∥AB交CE于点H,
由①知△EBC和△HDC均为等边三角形,
设AE=BD=x,则BE=BC=8﹣x,
∴DH=CD=8﹣2x,
∵DH∥AB,
∴=,即=,
∴x=2,
∵∠ACE=∠DAB,
∵△FAE∽△ACE,
∴=,
∵AC=AD=3AF,
∴=,EF=AE=.
22.(2021春?中原区校级月考)如图,在△ABC中,DM,EN分别垂直平分边AC和边BC,交边AB于M,N两点,DM与EN相交于点F.
(1)若AB=3cm,求△CMN的周长.
(2)若∠MFN=70°,求∠MCN的度数.
【解答】解:(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB=3(cm);
(2)∵∠MFN=70°,
∴∠MNF+∠NMF=180°﹣70°=110°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=110°,
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣110°=70°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°﹣2(∠A+∠B)=180°﹣2×70°=40°.
23.(2020秋?潮州期末)如图,在等边三角形ABC中,D是AB上的一点,E是CB延长线上一点,连接CD、DE,已知∠EDB=∠ACD.
(1)求证:△DEC是等腰三角形.
(2)当∠BDC=5∠EDB,EC=8时,求△EDC的面积.
【解答】(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵∠E+∠EDB=∠ABC=60°,∠ACD+∠DCB=60°,∠EDB=∠ACD,
∴∠E=∠DCE,
∴DE=DC,
∴△DEC是等腰三角形;
(2)解:设∠EDB=α,则∠BDC=5α,
∴∠E=∠DCE=60°﹣α,
∴6α+60°﹣α+60°﹣α=180°,
∴α=15°,
∴∠E=∠DCE=45°,
∴∠EDC=90°,
如图,过D作DH⊥CE于H,
∵△DEC是等腰直角三角形,
∴∠EDH=∠E=45°,
∴EH=HC=DH=EC=8=4,
∴△EDC的面积=EC?DH=8×4=16.
24.(2021?西城区校级模拟)(1)小My同学在网络直播课中学习了勾股定理,他想把这一知识应用在等边三角形中:边长为a的等边三角形面积是 a2 (用含a的代数式表示);
(2)小My同学进一步思考:是否可以将正方形剪拼成一个等边三角形(不重叠、无缝隙)?
①如果将一个边长为2的正方形纸片剪拼等边三角形,那么该三角形边长的平方是 ;
②小My同学按下图切割方法将正方形ABCD剪拼成一个等边三角形EFG:M、N分别为AB、CD边上的中点,P、Q是边BC、AD上两点,G为MQ上一点,且∠MGP=∠PGN=∠NGQ=60°.
请补全图形,画出拼成正三角形的各部分分割线,并标号;
③正方形ABCD的边长为2,设BP=x,则x2= ﹣1 .
【解答】解:(1)如图,过A作AD⊥BC于D,
∵△ABC是等边三角形,
∴BD=CD=BC=a,
∴AD===a,
∴S△ABC=BC?AD=a2;
(2)①∵边长为2的正方形的面积=4,
∴剪拼成的等边三角形的面积=4,
∴a2=4,
∴a2=,
即该三角形边长的平方是;
②补全图形如图2所示;
③由题意知,PG=PE,GN=NF,
∴PN是△GEF的中位线,
∴PN=EF,
∵N为AB边上的中点,
∴BN=AB=1,
∵边长为2的正方形的面积=4,
∴剪拼成的等边三角形的面积=4,
∴a2=4,
∴a2=,
即△GEF边长的平方是,
∴EF=,
∴PN=,
∵PN2=BN2+BP2,
∴=+1+x2,
∴x2=﹣1;
故答案为:(1)a2;(2)①;③﹣1;
25.(2020秋?五常市期末)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.
(1)求证:AB=AC;
(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.
【解答】证明:(1)过点A作AF⊥BC于点F,
∵AD=AE,
∴DF=EF,
∵BD=CE,
∴BF=CF,
∴AB=AC.
(2)∵∠B=∠BAD,∠C=∠EAC,∠BAE=∠BEA,∠ADC=∠DAC,
∴除△ABC与△ADE外所有的等腰三角形为:△ABD、△AEC、△ABE、△ADC,
26.(2020秋?临沭县期末)如图,在△ABC中,AB=AC,AD=DE=EB,BD=BC,试求∠A的度数.
【解答】解:设∠EBD=a,
∵AD=DE=BE,BD=BC,AC=AB,
∴∠A=∠AED,∠EBD=∠EDB=a,∠C=∠BDC=∠ABC,
∵∠AED=∠EBD+∠EDB=2∠EBD,
∴∠A=2∠EBD=2a,
∵∠BDC=∠A+∠EBD=3∠EBD=3a,
∴∠C=3∠EBD=3a,
∵∠A+∠C+∠ABC=180°,
∴2a+3a+3a=180°,
∴a=22.5°.
∴∠A=2a=45°.
27.(2020春?东明县期末)如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.
(1)求证:DF是线段AB的垂直平分线;
(2)当AB=AC,∠A=46°时,求∠EBC及∠F的度数.
【解答】(1)证明:∵∠A=∠ABE,
∴EA=EB,
∵AD=DB,
∴DF是线段AB的垂直平分线;
(2)解:∵∠A=46°,
∴∠ABE=∠A=46°,
∵AB=AC,
∴∠ABC=∠ACB=67°,
∴∠EBC=∠ABC﹣∠ABE=21°,
∠F=90°﹣∠ABC=23°.
28.(2019秋?巩义市期末)如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts.
(1)用含t的式子表示线段AP、AQ的长;
(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?
(3)当t为何值时,PQ∥BC?
【解答】解:(1)∵Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=30°.
又∵AB=12cm,
∴AC=6cm,BP=2t,AP=AB﹣BP=12﹣2t,AQ=t;
(2)∵△APQ是以PQ为底的等腰三角形,
∴AP=AQ,即12﹣2t=t,
∴当t=4时,△APQ是以PQ为底边的等腰三角形;
(3)当PQ⊥AC时,PQ∥BC.
∵∠C=90°,∠A=60°,
∴∠B=30°
∵PQ∥BC,
∴∠QPA=30°
∴AQ=AP,
∴t=(12﹣2t),解得t=3,
∴当t=3时,PQ∥BC.
29.(2020秋?朝阳期中)在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= 1:1 ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= 9 .
【解答】解:(1)
过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(×BD×AE):(×CD×AE)=1:1,
故答案为:1:1;
(2)
过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(×AB×DE):(×AC×DF)=m:n;
(3)
∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.
30.(2020春?揭西县期末)如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
【解答】(1)证明:
连接BE,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC﹣∠ABE=30°,
在Rt△BCE中,BE=2CE,
∴AE=2CE;
(2)解:△BCD是等边三角形,
理由如下:连接CD.
∵DE垂直平分AB,
∴D为AB中点,
∵∠ACB=90°,
∴CD=BD,
∵∠ABC=60°,
∴△BCD是等边三角形.
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
北师大新版专题复习《三角形的证明》
一.选择题(共10小题)
1.(2021春?江都区校级期末)等腰三角形的面积为24平方厘米,腰长8厘米.在底边上有一个动点P,则P到两腰的距离之和为( )
A.4cm
B.6cm
C.8cm
D.10cm
2.(2021?南山区校级二模)下列命题中真命题是( )
A.的算术平方根是3
B.数据a+2,a,a+3,a+2,a+3与2,0,3,2,3的方差相同
C.正六边形的内角和为360°
D.对角线相等的四边形是矩形
3.(2021春?武汉期中)已知等边三角形的边长为4,则其面积为( )平方单位.
A.4
B.8
C.12
D.16
4.(2021春?沙坪坝区期中)在△ABC中,∠A:∠B:∠C=2:5:3,则△ABC的形状是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
5.(2021?坪山区二模)如图,在△ABC中,∠B=90°,C是BD上一点,BC=10,∠ADB=45°,∠ACB=60°,则CD长为( )
A.10﹣
B.10﹣10
C.10﹣3
D.10﹣10
6.(2021春?汉寿县期中)如图,四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是( )
A.1
B.2
C.3
D.4
7.(2021?滨湖区一模)如图所示,在等边三角形ABC中,BC=6,E是中线AD上一点,现有一动点P沿着折线A﹣E﹣C运动,在AE上的速度是4单位/秒,在CE上的速度是2单位/秒,则点P从A运动到C所用时间最少时,AE长为( )
A.3
B.
C.
D.2
8.(2021?蜀山区一模)如图,在△ABC中,AB=AD,E为BD中点,连接AE,∠BAD=∠CAE,若BD=CD=6,则AB的长为( )
A.6
B.3
C.
D.
9.(2020秋?承德县期末)如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )
A.6
B.12
C.32
D.64
10.(2021?安徽模拟)如图,等边△ABC中,AB=10,E为AC中点,F,G为AB边上动点,且FG=5,则EF+CG的最小值是( )
A.5
B.5
C.5+5
D.15
二.填空题(共10小题)
11.(2021?天心区一模)如图,点O是三角形ABC内的一点,OA=OB=OC=4,∠BAC=45°,已知S△AOC﹣S△AOB=2,则∠BOC=
,S△ABC=
.
12.(2020秋?江岸区期末)如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,D为BC上一动点,EF垂直平分AD分别交AC于E、交AB于F,则BF的最大值为
.
13.(2021?巩义市模拟)点P是等边三角形ABC内部一点,过点P作三边的垂线,分别记为PH1,PH2,PH3,设△ABC的边长为a.若PH1=1,PH2=3,PH3=5,则a=
;若a=2,则PH1+PH2+PH3=
.
14.(2021春?金牛区校级期中)已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边△ABC的内部时,那么∠BOC和∠BPC的数量关系是:∠BOC=
.
15.(2020?皇姑区校级模拟)在平面直角坐标系中,A(0,3)、B(,0)、Q(0,),C是x轴上一点,以AC为边向右侧作正△ACD,P为AD的中点.当C从O运动到B点时,PQ的最小值为
.
16.(2020春?新都区期末)边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点顺次连接,又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图)…,按此方式依次操作,则第7个正六边形的边长是
.
17.(2019?雁塔区校级四模)如图,在四边形ABCD中,BD平分∠ABC,CD⊥BD于D,AC=5,边BC与AB的长度差为2,当△ADC面积最大时,边AD的长为
.
18.(2021?长沙模拟)如图,△ABC中,AD平分∠BAC,∠ACB=3∠B,CE⊥AD,AC=8,BC=BD,则CE=
.
19.(2018秋?江岸区期末)如图,已知∠AOB=α(0°<α<60°),射线OA上一点M,以OM为边在OA下方作等边△OMN,点P为射线OB上一点,若∠MNP=α,则∠OMP=
.
20.(2019?鄞州区一模)如图,△ABC中,AB=AC=15,∠BAC=120°,小明要将该三角形分割成两个直角三角形和两个等腰三角形,他想出了如下方案:在AB上取点D,过点D画DE∥AC交BC于点E,连接AE,在AC上取合适的点F,连接EF可得到4个符合条件的三角形,则满足条件的AF长是
.
三.解答题(共10小题)
21.(2021?蔡甸区二模)如图,△ABC中,点D在BC边上,且∠ADB=90°∠CAD.
(1)求证:AD=AC;
(2)点E在AB边上,连接CE交AD于点F,且∠CFD=∠CAB,AE=BD,
①求∠ABC的度数;
②若AB=8,DF=2AF,直接写出EF的长.
22.(2021春?中原区校级月考)如图,在△ABC中,DM,EN分别垂直平分边AC和边BC,交边AB于M,N两点,DM与EN相交于点F.
(1)若AB=3cm,求△CMN的周长.
(2)若∠MFN=70°,求∠MCN的度数.
23.(2020秋?潮州期末)如图,在等边三角形ABC中,D是AB上的一点,E是CB延长线上一点,连接CD、DE,已知∠EDB=∠ACD.
(1)求证:△DEC是等腰三角形.
(2)当∠BDC=5∠EDB,EC=8时,求△EDC的面积.
24.(2021?西城区校级模拟)(1)小My同学在网络直播课中学习了勾股定理,他想把这一知识应用在等边三角形中:边长为a的等边三角形面积是
(用含a的代数式表示);
(2)小My同学进一步思考:是否可以将正方形剪拼成一个等边三角形(不重叠、无缝隙)?
①如果将一个边长为2的正方形纸片剪拼等边三角形,那么该三角形边长的平方是
;
②小My同学按下图切割方法将正方形ABCD剪拼成一个等边三角形EFG:M、N分别为AB、CD边上的中点,P、Q是边BC、AD上两点,G为MQ上一点,且∠MGP=∠PGN=∠NGQ=60°.
请补全图形,画出拼成正三角形的各部分分割线,并标号;
③正方形ABCD的边长为2,设BP=x,则x2=
.
25.(2020秋?五常市期末)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.
(1)求证:AB=AC;
(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.
26.(2020秋?临沭县期末)如图,在△ABC中,AB=AC,AD=DE=EB,BD=BC,试求∠A的度数.
27.(2020春?东明县期末)如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.
(1)求证:DF是线段AB的垂直平分线;
(2)当AB=AC,∠A=46°时,求∠EBC及∠F的度数.
28.(2019秋?巩义市期末)如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts.
(1)用含t的式子表示线段AP、AQ的长;
(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?
(3)当t为何值时,PQ∥BC?
29.(2020秋?朝阳期中)在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD=
;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC=
.
30.(2020春?揭西县期末)如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
北师大新版数学专题复习《三角形的证明》
参考答案与试题解析
一.选择题(共10小题)
1.(2021春?江都区校级期末)等腰三角形的面积为24平方厘米,腰长8厘米.在底边上有一个动点P,则P到两腰的距离之和为( )
A.4cm
B.6cm
C.8cm
D.10cm
【解答】解:已知:△ABC中,PE⊥AB于E,PF⊥AC于F,AB=AC=8厘米,△ABC的面积为24平方厘米,P是底边BC上一个动点.
求:PE+PF的值.
解:连接AP,
∵PE⊥AB,PF⊥AC,
∴S△ABP=AB?PE,S△ACP=AC?PF,
∵S△ABP+S△ACP=S△ABC,S△ABC=24,
∴AB?PE+AC?PF=24,
∴AB(PE+PF)=24,
∴PE+PF==6cm,
故选:B.
2.(2021?南山区校级二模)下列命题中真命题是( )
A.的算术平方根是3
B.数据a+2,a,a+3,a+2,a+3与2,0,3,2,3的方差相同
C.正六边形的内角和为360°
D.对角线相等的四边形是矩形
【解答】解:A、的算术平方根是,本选项错误,不符合题意.
B、数据a+2,a,a+3,a+2,a+3与2,0,3,2,3的方差相同,正确,本选项符合题意.
C、正六边形的内角和为360°,错误,应该是720°,本选项不符合题意.
D、对角线相等的四边形是矩形,错误,应该是对角线相等的平行四边形是矩形,本选项不符合题意.
故选:B.
3.(2021春?武汉期中)已知等边三角形的边长为4,则其面积为( )平方单位.
A.4
B.8
C.12
D.16
【解答】解:如图,等边三角形ABC,AB=BC=4,
作AD⊥BC,垂足为D,
∴BD=CD=2,
在Rt△ABD中,AD=,
∴S△ABC=BC?AD
=×4×
=,
故选:A.
4.(2021春?沙坪坝区期中)在△ABC中,∠A:∠B:∠C=2:5:3,则△ABC的形状是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
【解答】解:设∠A=2x°,∠B=5x°,∠C=3x°,
∵∠A+∠B+∠C=180°,
∴2x+5x+3x=180,
解得:x=18,
∴∠B=5x°=90°,
∴△ABC是直角三角形,
故选:B.
5.(2021?坪山区二模)如图,在△ABC中,∠B=90°,C是BD上一点,BC=10,∠ADB=45°,∠ACB=60°,则CD长为( )
A.10﹣
B.10﹣10
C.10﹣3
D.10﹣10
【解答】解:∵在△ABC中,∠B=90°,∠ACB=60°,
∴∠CAB=30°,
∴BC=AC,
∴AC=2BC=20,
∴AB==10,
∵∠ADB=45°,
∴∠DAB=45°,
∴∠DAB=∠ADB,
∴BD=AB=10,
∴CD=BD﹣BC=10﹣10,
故选:B.
6.(2021春?汉寿县期中)如图,四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是( )
A.1
B.2
C.3
D.4
【解答】解:∵BD⊥CD,∠A=90°
∴∠ABD+∠ADB=90°,
∠CBD+∠C=90°,
∴∠ABD=∠CBD,
由垂线段最短得,DP⊥BC时DP最小,
此时,DP=AD=3.
故选:C.
7.(2021?滨湖区一模)如图所示,在等边三角形ABC中,BC=6,E是中线AD上一点,现有一动点P沿着折线A﹣E﹣C运动,在AE上的速度是4单位/秒,在CE上的速度是2单位/秒,则点P从A运动到C所用时间最少时,AE长为( )
A.3
B.
C.
D.2
【解答】解:作CM⊥AB于点M,点P在A﹣E﹣C上运动时间为+,=(),
∵∠BAD=30°,
∴EM=AE,
∴()=(EM+CE),
当C,E,M共线时,点P运动时间最短,
∴CM为三角形中线,点E为重心,
∵∠CAD=30°,CD=BC=3,
∴AD=CD=3,
AE=AD=2.
故选:D.
8.(2021?蜀山区一模)如图,在△ABC中,AB=AD,E为BD中点,连接AE,∠BAD=∠CAE,若BD=CD=6,则AB的长为( )
A.6
B.3
C.
D.
【解答】解:过点D作DF⊥AC于F,如图:
∵AB=AD,E为BD中点,
∴AE⊥BD,∠BAE=∠DAE.
∵BD=CD=6,
∴BE=DE=3,CD=4.
∵∠BAD=∠CAE,
∴∠BAE=∠DAE=∠DAF,
∴DF=DE=3,FC==.
∵∠CFD=∠AEC=90°,∠C=∠C,
∴△CFD∽△CEA,即,AE=3.
∴AB===6.
故选:A.
9.(2020秋?承德县期末)如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则B6B7的边长为( )
A.6
B.12
C.32
D.64
【解答】解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2=2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:A7B7=26B1A2=26=64,B6A7==32,△B7B6A7是直角三角形,∠B7B6A7=90°,
∴B6B7===32.
故选:C.
10.(2021?安徽模拟)如图,等边△ABC中,AB=10,E为AC中点,F,G为AB边上动点,且FG=5,则EF+CG的最小值是( )
A.5
B.5
C.5+5
D.15
【解答】解:如图:
作C点关于AB的对称点C′,
则C'G=CG,
取BC的中点Q,
连接EQ,GQ,
∵点E是AC的中点,
∴EQ=AB=5=FG,EQ∥AB,
∴四边形EFGQ是平行四边形,
∴EF=GQ,
∴当点C',G,Q在同一条线上时,CG+EF最小,
作C′H⊥BC交BC的延长线于点H,
∵BC=BC′=10,∠CBC′=120°,
∴HC′=5,HB=5,
∴HQ=10,
∴C′Q==5,
∴EF+CG的最小值是5.
故选:A.
二.填空题(共10小题)
11.(2021?天心区一模)如图,点O是三角形ABC内的一点,OA=OB=OC=4,∠BAC=45°,已知S△AOC﹣S△AOB=2,则∠BOC= 90° ,S△ABC= 8+2 .
【解答】解:∵OA=OB=OC=4,
∴△ABC是以O为圆心,半径为4的内接三角形,
延长AO交BC于点E,作BM⊥AE,CN⊥AE,
∵∠BAC=45°,
∴∠BOC=2∠BAC=90°,
∴BC=OB=4,
∵S△AOC﹣S△AOB=2,
∴AO?CN﹣AO?BM=2(CN﹣BM)=2,
∴CN﹣BM=1.
∵∠BOM+∠CON=90°,∠BOM+∠OBM=90°,
∴∠CON=∠OBM,
又∵∠BMO=∠CNO=90°,OB=OC,
在△BOM和△CON中,
∴△BOM≌△CON(AAS),
∴OM=CN,
在Rt△BOM和Rt△CON中,由勾股定理得:
BM2+OM2=ON2+CN2=16,
即BM2+CN2=16,
联立方程,
解得BM=或BM=(舍).
∴CN=BM+1=.
∴S△AOC+S△AOB=AO?CN+AO?BM=2(CN+BM)=2.
∵S△BOC=OB?OC=8,
∴S△ABC=S△AOC+S△AOB+S△BOC=8+2.
故答案为:90°,8+2.
12.(2020秋?江岸区期末)如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,D为BC上一动点,EF垂直平分AD分别交AC于E、交AB于F,则BF的最大值为 .
【解答】解:∵Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,
∴AB=2AC=4,
∵EF垂直平分AD,
∴AF=DF,
若要使BF最大,则AF需要最小,
∴以F为圆心,AF为半径的圆与BC相切即可,
∴FD⊥BD,
∴AB=AF+2AF=4,
∴AF=,
∴BF的最大值为4﹣=,
故答案为:.
【点评】本题主要考查了线段垂直平分线的性质、30°角所对直角边是斜边的一半以及圆与直线的位置关系,将BF的最大值转化为AF最小是解决本题的关键,属于压轴题.
13.(2021?巩义市模拟)点P是等边三角形ABC内部一点,过点P作三边的垂线,分别记为PH1,PH2,PH3,设△ABC的边长为a.若PH1=1,PH2=3,PH3=5,则a= 6 ;若a=2,则PH1+PH2+PH3= 3 .
【解答】解:连结PA,PB,PC,设△ABC的BC边上的高为h,则h=AB?sin60°=a,
∴S△ABC==×a×a=a2,
∵S△ABC=S△ABP+S△BCP+S△ACP,
∴a2=,
解得a=6;
当a=2时,
∵S△ABC=S△ABP+S△BCP+S△ACP,
∴×(2)2=×++,
∴PH1+PH2+PH3=3.
故答案为:6;3.
【点评】本题考查了等边三角形的性质,利用等面积法列出方程是解题的关键.
14.(2021春?金牛区校级期中)已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边△ABC的内部时,那么∠BOC和∠BPC的数量关系是:∠BOC= 4∠BPC﹣360° .
【解答】解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(
∠ABC+∠ACB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC,
即∠BAC=2∠BPC﹣180°;
如图,连接AO.
∵点O是这个三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,
∴∠BOC=360°﹣(∠AOB+∠AOC)
=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC
=2(2∠BPC﹣180°)
=4∠BPC﹣360°,
故答案为:4∠BPC﹣360°.
15.(2020?皇姑区校级模拟)在平面直角坐标系中,A(0,3)、B(,0)、Q(0,),C是x轴上一点,以AC为边向右侧作正△ACD,P为AD的中点.当C从O运动到B点时,PQ的最小值为 .
【解答】解:如图,连接OP,CP,
∵正△ACD中,P为AD的中点,
∴∠AOB=∠APC=90°,
∴O、A、P、C四点共圆,
∴∠AOP=∠ACP=30°,
∴当PQ⊥OP时,PQ最小,
即PQ的最小值为OQ=×=.
故答案为:.
16.(2020春?新都区期末)边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点顺次连接,又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图)…,按此方式依次操作,则第7个正六边形的边长是 ×()6a .
【解答】解:如图1,连接AD、DF、DB.
∵六边形ABCDEF是正六边形,
∴∠ABC=∠BAF=∠AFE,AB=AF,∠E=∠C=120°,EF=DE=BC=CD,
∴∠EFD=∠EDF=∠CBD=∠BDC=30°,
∵∠AFE=∠ABC=120°,
∴∠AFD=∠ABD=90°,
在Rt△ABD和RtAFD中,
∵,
∴Rt△ABD≌Rt△AFD(HL),
∴∠BAD=∠FAD=×120°=60°,
∴∠FAD+∠AFE=60°+120°=180°,
∴AD∥EF,
∵G、I分别为AF、DE中点,
∴GI∥EF∥AD,
∴∠FGI=∠FAD=60°,
∵六边形ABCDEF是正六边形,△QKM是等边三角形,
∴∠EDM=60°=∠M,
∴ED=EM,
同理AF=QF,
即AF=QF=EF=EM,
∵等边三角形QKM的边长是a,
∴第一个正六边形ABCDEF的边长是a,即等边三角形QKM的边长的,
如图2,过F作FZ⊥GI于Z,过E作EN⊥GI于N,
则FZ∥EN,
∵EF∥GI,
∴四边形FZNE是平行四边形,
∴EF=ZN=a,
∵GF=AF=×a=a,∠FGI=60°(已证),
∴∠GFZ=30°,
∴GZ=GF=a,
同理IN=a,
∴GI=a+a+a=a,即第二个等边三角形的边长是a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是×a;
同理第三个等边三角形的边长是×a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是××a;
同理第四个等边三角形的边长是()3a,第四个正六边形的边长是×()3a;
第五个等边三角形的边长是()4a,第五个正六边形的边长是×()4a;
…
第n个正六边形的边长是×()n﹣1a,
∴第七个正六边形的边长是×()6a.
故答案为:×()6a.
17.(2019?雁塔区校级四模)如图,在四边形ABCD中,BD平分∠ABC,CD⊥BD于D,AC=5,边BC与AB的长度差为2,当△ADC面积最大时,边AD的长为 .
【解答】解:延长CD与BA交于点E,
∵BD平分∠ABC,CD⊥BD于D,
∴△CAE为等腰三角形,D为CE中点,
∴S△ADC=S△ACE=S△ADE.
∵BC﹣AB=2,
∴AE=2,
当AE⊥AC时,△AEC面积最大,
∴此时△ADC面积最大.
∵CE===,
∴AD=CE=.
故答案为:.
18.(2021?长沙模拟)如图,△ABC中,AD平分∠BAC,∠ACB=3∠B,CE⊥AD,AC=8,BC=BD,则CE= .
【解答】解:延长CE交AB于F,过点D作DH⊥AB于H,DN⊥AC于N,过点A作AM⊥BC于M,如图所示:
∵CE⊥AD,
∴∠AEF=∠AEC=90°,
∵AD平分∠BAC,
∴∠FAE=∠CAE,DH=DN,
在△AEF与△AEC中,,
∴△AEF≌△AEC(ASA),
∴AF=AC=8,∠AFE=∠ACE,EF=CE,
∵∠AFC=∠B+∠ECD,
∴∠ACF=∠B+∠ECD,
∴∠ACB=2∠ECD+∠B,
∵∠ACB=3∠B,
∴2∠ECD+∠B=3∠B,
∴∠B=∠ECD,
∴CF=BF,
∵BC=BD,
∴=,
S△ADB=DH?AB=AM?BD,S△ACD=DN?AC=AM?CD,
∴=,
即==,
∴AB=AC=,
∴CF=BF=﹣8=,
∴CE=CF=,
故答案为:.
19.(2018秋?江岸区期末)如图,已知∠AOB=α(0°<α<60°),射线OA上一点M,以OM为边在OA下方作等边△OMN,点P为射线OB上一点,若∠MNP=α,则∠OMP= 30°或120°﹣α. .
【解答】解:(1)当P位于MN左侧时,如图1,
∵△OMN是等边三角形,
∴MN=MO=ON,∠MON=∠MNO=60°,
∵∠MNP=∠AOB=α,
∴∠PON=∠PNO,
∴PO=PN,
△MPO≌△MPN,(SAS)
∴∠OMP=∠NMP=∠OMN=×60°=30°
(2)当P位于MN右侧时,如图2,将△MNP绕着点M顺时针旋转60°得到△MOQ,
此时△MPQ是等边三角形,
∴∠MPQ=60°,
∴∠OMP=180°﹣∠MPQ﹣∠MOP=180°﹣60°﹣α=120°﹣α,
故答案为:30°或120°﹣α.
20.(2019?鄞州区一模)如图,△ABC中,AB=AC=15,∠BAC=120°,小明要将该三角形分割成两个直角三角形和两个等腰三角形,他想出了如下方案:在AB上取点D,过点D画DE∥AC交BC于点E,连接AE,在AC上取合适的点F,连接EF可得到4个符合条件的三角形,则满足条件的AF长是 5、10或 .
【解答】解:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE∥AC,
∴∠DEB=∠C=30°,∠BDE=120°,
∴△BDE是等腰三角形,∠ADE=180°﹣∠BDE=60°.
被分割的四个三角形中有两个直角三角形和两个等腰三角形.
①当∠AED=90°时,如图1:
∴∠DAE=180°﹣∠AED﹣∠ADE=30°,
∴∠EAF=∠BAC﹣∠DAE=90°.
则△EFC是等腰三角形.
∵∠AEC=180°﹣∠BED﹣∠DEA=60°,
∴△EFC是等腰三角形只可能存在∠FEC=∠C=30°的情况,
设AF=x,
∵∠AEF=180°﹣∠BED﹣∠AED﹣∠FEC=30°,
∴EF=2x,
∵EF=FC=2x,
∴AF+FC=3x=AC=15,
∴AF=5.
②当∠DAE=90°且∠AEF=90°时,如图2:
此时∠EAF=∠BAC﹣∠DAE=30°,
∴∠AFE=180°﹣∠AEF﹣∠EAF=60°
设AF=x,则EF=x,
∵∠EFC=180°﹣∠AFE=120°,
又∵∠FEC=180°﹣∠C﹣∠EFC=30°,
∴△EFC是等腰三角形,CF=EF=x,
∵AC=AF+FC=x+x=15,
∴AF=x=10.
③当∠DAE=90°且∠FEC=90°时,如图3.
∠FAE=∠BAC﹣∠DAE=30°,
∵∠AED=180°﹣∠DAE﹣∠ADE=30°,
∴∠AEF=180°﹣∠BED﹣∠FEC﹣∠AED=30°.
∴AF=AE,
设AF=EF=x,
∵∠FEC=90°,∠C=30°,
∴CF=2x,
∵AF+FC=x+2x=3x=AC=15,
∴AF=x=5.
④当∠AFE=∠EFC=90°时,则△ADE是等腰三角形,如图4
∵∠ADE=60°,
∴∠DAE=∠AED=60°,
∵∠EAF=∠BAC﹣∠DAE=60°,
∴∠AEF=180°﹣∠EAF﹣∠AFE=30°.
设AF=x,则EF=x.
∵∠EFC=90°,∠C=30°,
∴FC=EF=3x,
∵AC=AF+FC=x+3x=4x=15,
∴AF=.
故答案为:5、10或
三.解答题(共10小题)
21.(2021?蔡甸区二模)如图,△ABC中,点D在BC边上,且∠ADB=90°∠CAD.
(1)求证:AD=AC;
(2)点E在AB边上,连接CE交AD于点F,且∠CFD=∠CAB,AE=BD,
①求∠ABC的度数;
②若AB=8,DF=2AF,直接写出EF的长.
【解答】解:(1)∵∠ADB=∠ACB+∠CAD,∠ADB=90°∠CAD,
∴∠ACB=∠ADB﹣∠CAD=90°∠CAD,
∵∠ADB+∠CDA=180°,
∴∠CDA=180°﹣∠ADB=180°﹣(90°∠CAD)=90°∠CAD,
∴∠ACB=∠ADC,
∴AD=AC;
(2)①过点D作DG∥CE交AB于点G,
∵∠CFD=∠CAB,∠CFD=∠CAD+∠ACE,∠CAB=∠CAD+∠DAB,
∴∠ACE=∠DAB,
又∵∠ACD=∠ADC,∠ECB=∠ACD﹣∠ACE,∠B=∠ADC﹣∠DAB,
∴∠ECB=∠B,
∴CE=BE,
∵DG∥CE,
∴∠ECB=∠BDG,
∴∠BDG=∠B,
∴DG=BG,
∵∠AEC=∠DGA,AC=DA,∠ACE=∠DAG,
∴△AEC≌△DGA(AAS),
∴DG=AE,
又∵AE=BD,
∴DG=BD=BG,
∴△BDG为等边三角形,
∴∠ABC=60°;
②EF=.
过点D作DH∥AB交CE于点H,
由①知△EBC和△HDC均为等边三角形,
设AE=BD=x,则BE=BC=8﹣x,
∴DH=CD=8﹣2x,
∵DH∥AB,
∴=,即=,
∴x=2,
∵∠ACE=∠DAB,
∵△FAE∽△ACE,
∴=,
∵AC=AD=3AF,
∴=,EF=AE=.
22.(2021春?中原区校级月考)如图,在△ABC中,DM,EN分别垂直平分边AC和边BC,交边AB于M,N两点,DM与EN相交于点F.
(1)若AB=3cm,求△CMN的周长.
(2)若∠MFN=70°,求∠MCN的度数.
【解答】解:(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB=3(cm);
(2)∵∠MFN=70°,
∴∠MNF+∠NMF=180°﹣70°=110°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=110°,
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣110°=70°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°﹣2(∠A+∠B)=180°﹣2×70°=40°.
23.(2020秋?潮州期末)如图,在等边三角形ABC中,D是AB上的一点,E是CB延长线上一点,连接CD、DE,已知∠EDB=∠ACD.
(1)求证:△DEC是等腰三角形.
(2)当∠BDC=5∠EDB,EC=8时,求△EDC的面积.
【解答】(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵∠E+∠EDB=∠ABC=60°,∠ACD+∠DCB=60°,∠EDB=∠ACD,
∴∠E=∠DCE,
∴DE=DC,
∴△DEC是等腰三角形;
(2)解:设∠EDB=α,则∠BDC=5α,
∴∠E=∠DCE=60°﹣α,
∴6α+60°﹣α+60°﹣α=180°,
∴α=15°,
∴∠E=∠DCE=45°,
∴∠EDC=90°,
如图,过D作DH⊥CE于H,
∵△DEC是等腰直角三角形,
∴∠EDH=∠E=45°,
∴EH=HC=DH=EC=8=4,
∴△EDC的面积=EC?DH=8×4=16.
24.(2021?西城区校级模拟)(1)小My同学在网络直播课中学习了勾股定理,他想把这一知识应用在等边三角形中:边长为a的等边三角形面积是 a2 (用含a的代数式表示);
(2)小My同学进一步思考:是否可以将正方形剪拼成一个等边三角形(不重叠、无缝隙)?
①如果将一个边长为2的正方形纸片剪拼等边三角形,那么该三角形边长的平方是 ;
②小My同学按下图切割方法将正方形ABCD剪拼成一个等边三角形EFG:M、N分别为AB、CD边上的中点,P、Q是边BC、AD上两点,G为MQ上一点,且∠MGP=∠PGN=∠NGQ=60°.
请补全图形,画出拼成正三角形的各部分分割线,并标号;
③正方形ABCD的边长为2,设BP=x,则x2= ﹣1 .
【解答】解:(1)如图,过A作AD⊥BC于D,
∵△ABC是等边三角形,
∴BD=CD=BC=a,
∴AD===a,
∴S△ABC=BC?AD=a2;
(2)①∵边长为2的正方形的面积=4,
∴剪拼成的等边三角形的面积=4,
∴a2=4,
∴a2=,
即该三角形边长的平方是;
②补全图形如图2所示;
③由题意知,PG=PE,GN=NF,
∴PN是△GEF的中位线,
∴PN=EF,
∵N为AB边上的中点,
∴BN=AB=1,
∵边长为2的正方形的面积=4,
∴剪拼成的等边三角形的面积=4,
∴a2=4,
∴a2=,
即△GEF边长的平方是,
∴EF=,
∴PN=,
∵PN2=BN2+BP2,
∴=+1+x2,
∴x2=﹣1;
故答案为:(1)a2;(2)①;③﹣1;
25.(2020秋?五常市期末)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.
(1)求证:AB=AC;
(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.
【解答】证明:(1)过点A作AF⊥BC于点F,
∵AD=AE,
∴DF=EF,
∵BD=CE,
∴BF=CF,
∴AB=AC.
(2)∵∠B=∠BAD,∠C=∠EAC,∠BAE=∠BEA,∠ADC=∠DAC,
∴除△ABC与△ADE外所有的等腰三角形为:△ABD、△AEC、△ABE、△ADC,
26.(2020秋?临沭县期末)如图,在△ABC中,AB=AC,AD=DE=EB,BD=BC,试求∠A的度数.
【解答】解:设∠EBD=a,
∵AD=DE=BE,BD=BC,AC=AB,
∴∠A=∠AED,∠EBD=∠EDB=a,∠C=∠BDC=∠ABC,
∵∠AED=∠EBD+∠EDB=2∠EBD,
∴∠A=2∠EBD=2a,
∵∠BDC=∠A+∠EBD=3∠EBD=3a,
∴∠C=3∠EBD=3a,
∵∠A+∠C+∠ABC=180°,
∴2a+3a+3a=180°,
∴a=22.5°.
∴∠A=2a=45°.
27.(2020春?东明县期末)如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.
(1)求证:DF是线段AB的垂直平分线;
(2)当AB=AC,∠A=46°时,求∠EBC及∠F的度数.
【解答】(1)证明:∵∠A=∠ABE,
∴EA=EB,
∵AD=DB,
∴DF是线段AB的垂直平分线;
(2)解:∵∠A=46°,
∴∠ABE=∠A=46°,
∵AB=AC,
∴∠ABC=∠ACB=67°,
∴∠EBC=∠ABC﹣∠ABE=21°,
∠F=90°﹣∠ABC=23°.
28.(2019秋?巩义市期末)如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts.
(1)用含t的式子表示线段AP、AQ的长;
(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?
(3)当t为何值时,PQ∥BC?
【解答】解:(1)∵Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=30°.
又∵AB=12cm,
∴AC=6cm,BP=2t,AP=AB﹣BP=12﹣2t,AQ=t;
(2)∵△APQ是以PQ为底的等腰三角形,
∴AP=AQ,即12﹣2t=t,
∴当t=4时,△APQ是以PQ为底边的等腰三角形;
(3)当PQ⊥AC时,PQ∥BC.
∵∠C=90°,∠A=60°,
∴∠B=30°
∵PQ∥BC,
∴∠QPA=30°
∴AQ=AP,
∴t=(12﹣2t),解得t=3,
∴当t=3时,PQ∥BC.
29.(2020秋?朝阳期中)在△ABC中,D是BC边上的点(不与点B、C重合),连接AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= 1:1 ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= 9 .
【解答】解:(1)
过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(×BD×AE):(×CD×AE)=1:1,
故答案为:1:1;
(2)
过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(×AB×DE):(×AC×DF)=m:n;
(3)
∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.
30.(2020春?揭西县期末)如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
【解答】(1)证明:
连接BE,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC﹣∠ABE=30°,
在Rt△BCE中,BE=2CE,
∴AE=2CE;
(2)解:△BCD是等边三角形,
理由如下:连接CD.
∵DE垂直平分AB,
∴D为AB中点,
∵∠ACB=90°,
∴CD=BD,
∵∠ABC=60°,
∴△BCD是等边三角形.
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
