鲁教版(五四制)六年级上册数学 4.3 一元一次方程的应用(1) 课件(共13张ppt)
文档属性
| 名称 | 鲁教版(五四制)六年级上册数学 4.3 一元一次方程的应用(1) 课件(共13张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 125.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 08:16:36 | ||
图片预览





文档简介
(共13张PPT)
一元一次方程的应用——形积变化问题
将一个底面半径为6cm、高为40cm的“瘦长”圆柱形钢材锻压成底面半径为12cm的“矮胖”圆柱形零件毛坯,请问毛坯的高是多少?
解析
举一反三
有一根钢管长12米,要锯成两段,使第一段比第二段短2米,每段各长多少米?
解:设第二段长为x米,则第一段长为(x-2)米,由题意得:
x+(x-2)=12
解得x=7
则7-2=5(米)
答:第一段长5米,第二段长7米。
解:设毛坯的高为xcm,由题意得:
π×
×40
=π×
×x
x
=
10
答:毛坯的高是10cm。
一元一次方程的应用——打折销售问题
解析
举一反三
某服装进货价为80元/件,标价为200元/件,商店将此服装打x折销售后仍获利50%,则x为(
)
A.5
B.6
C.7
D.8
解:设最低打x折出售此商品,由题意得:
x
=
7
答:打7折出售此商品。
某商品进价为400元,标价为600元,商店要求以利润率不低于5%的售价打折出售,最低可以打几折出售此商品?
B
一元一次方程的应用——含两个等量关系的问题
某足球赛即将举行,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为5800元。
其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?
解析
解:设小李预定了小组赛球票x张,则
小组赛球票
淘汰赛球票
票数/张
x
票款/元
小组赛票款
+
淘汰赛票款
=
5800元
10-x
550x
700(10-x)
550x+700(10-x)=
5800
x
=
8
则10-x
=
10-8
=
2(张)
答:小李预定了小组赛球票8张,淘汰赛球票2张。
举一反三
某车间原计划13小时生产一批零件,实际每小时多生产了10件,用了12小时不但完成了任务,而且还多生产了60件,设原计划每小时生产x个零件,那么下列方程正确的是(
)
A.
13x=12(x+10)+60
B.
12(x+10)=13x+60
C.
D.
B
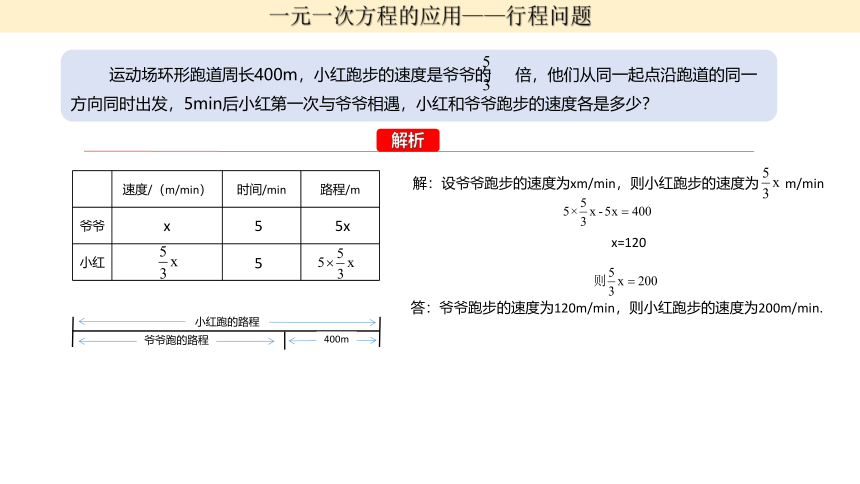
一元一次方程的应用——行程问题
运动场环形跑道周长400m,小红跑步的速度是爷爷的
倍,他们从同一起点沿跑道的同一方向同时出发,5min后小红第一次与爷爷相遇,小红和爷爷跑步的速度各是多少?
解析
速度/(m/min)
时间/min
路程/m
爷爷
x
小红
小红跑的路程
爷爷跑的路程
400m
解:设爷爷跑步的速度为xm/min,则小红跑步的速度为
m/min
x=120
答:爷爷跑步的速度为120m/min,则小红跑步的速度为200m/min.
5
5
5x
一元一次方程的应用——本息问题
王大伯3年前把手头一笔钱作为3年定期存款存入银行,年利率为5%,到期后得到本息共23000元,问当年王大伯存入银行多少钱?
解:设当年王大伯存入银行x元,由题意得
x+3×5%x
=
23000
解得
x
=
20000
解析
答:当年王大伯存入银行20000元.
利息=本金×利率×年数
本息和=本金+利息
=本金×(1+利率×期数)
举一反三
王先生到银行存了一笔三年期的
定期存款,年利率是4.25%,若到期后取出得到本息和(本金+利息)33825元。设王先生存入的本金为x元,则下面所列方程正确的是(
)
A.x+3×4.25%x=33825
B.x+4.25%x=33825
C.3×4.25%x=33825
D.3(x+4.25%x)=33825
A
一元一次方程的应用——工程问题
刺绣一件作品,甲单独绣需要15天完成,乙单独绣需要12天完成。现在甲先单独绣1天,接着乙又单独绣4天,剩下的工作由甲、乙两人合绣。问再绣多少天可以完成这件作品?
解析
解:设再绣x天可以完成这件作品,由题意得
解得
x=4
答:再绣4天可以完成这件作品。
用整体“1”表示总工作量!
工作量
=
工作效率×工作时间
路程
=
速度
×
时间
一元一次方程的应用——古代数学问题
《九章算术》中有“盈不足术”的问题,原文如下:“今有共買羊,人出五,不足四十五;人出七,不足三。问人数、羊價各幾何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元。问:人数和羊价各是多少?
解析
解:设买羊人数为x人,则羊的单价为(5x+45)元,由题意得
5x+45
=
7x+3
x
=
21
故5×21+45=150(元)
答:买羊人数为21人,羊的单价为150元.
举一反三
明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:所分的银子共有(
)两。(注:明代时1斤=16两,故有“半斤八两”这个成语)
46
一元一次方程的应用——顺水(逆水)问题
一艘船从甲码头到乙码头顺流行驶,用了2h,从乙码头返回甲码头逆流形式比顺流行驶多用了0.5h,已知水流的速度是3km/h,则船在静水中的速度是多少?
解析
解:设船在静水中的速度是xkm/h,则顺流时的速度为(x+3)km/h,逆流时的速度为(x-3)km/h,由题意得
2(x+3)=
2.5(x-3)
x
=
27
答:船在静水中的速度是27km/h。
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
举一反三
一艘轮船在A,B两港口之间行驶,顺水航行需要5h,逆水航行需要7h,水流的速度是5km/h,则A,B两港口之间的路程是(
)
A.105km
B.175km
C.180km
D.210km
B
一元一次方程的应用——周长问题
一个长方形的周长为30cm,若这个长方形的长减少1cm,宽增加2cm就可成为一个正方形,设长方形的长为xcm,可列方程为(
)
解析
举一反三
1.某小区在规划设计时,准备在两栋楼房之间设置一块周长为120米的长方形绿地,并且长比宽多10米。设绿地的宽为x米,根据题意,列出的方程是(
)
2.如右图,在周长为10m的长方形窗户上钉一块宽为1m的长方形遮阳布,使透光部分正好是一正方形,则定钉好后透光面积为(
)
(第2题图)
2[x+(x+10)]=120
4平方米
x-1=(15-x)+2
x
15-x
x-1
(15-x)+2
(长+宽)×2=周长
(长+宽)=周长÷2
一元一次方程的应用——面积问题
如图,小红将一个正方形纸片剪去一个宽为4厘米的长条后,再从剩下的长方形纸片上剪去一个宽为5厘米的长条,且剪下的两个长条的面积相等。正方形的边长为多少厘米?设正方形的边长为x厘米,则可列方程_____________________,解方程可知正方形的边长为_____________厘米。
解析
5cm
4cm
举一反三
在梯形面积公式
中,已知h=6厘米,a=3厘米,S=24平方厘米,则b等于(
)
A.1厘米
B.5厘米
C.3厘米
D.4厘米
B
4x=5(x-4)
20
xcm
(x-4)cm
4x=5(x-4)
4x=5x-20
20=5x-4x
x=20
一元一次方程的应用——等积变换问题
如图,在水平桌面上有甲、乙两个内部呈圆柱形、高度相同的容器,内部底面积分别为80平方厘米,100平方厘米,且甲容器装满水,乙容器是空的,若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲中的水位高度低了8cm,则甲的容积为(
)
解析
举一反三
有一个长、宽、高分别是15cm,10cm,30cm的长方体钢锭,现将它锻压成一个底面为正方形,且边长为15cm的长方体钢锭,高变成了__________.
甲
乙
乙
8cm
xcm
圆柱体积
=
底面积
×
高
x
=
40
40×80=3200立方厘米
20cm
一元一次方程的应用——比例问题
某中学在“献爱心”活动中,六年级五个班共捐款6300元,其中一班捐款1400元,二班比一班少捐款100元,三班捐款数是年级总数的20%,四班与五班捐款数之比是6:7.求四班捐款多少元?
解析
举一反三
一个三角形的三条边的长度之比为2:4:5,最长的边比最短的边长6cm,求该三角形的周长。
四班与五班捐款的总数:6300-1400-(1400-100)-6300×20%=2340(元)
设四班捐款为6x元,五班捐款为7x元,
6x+7x=2340
x=180,则6x=1080
22cm
一班:1400元
二班:1400-100
三班:6300×20%
一元一次方程的应用——阶梯计费问题
某城市自来水收费实行阶梯水价,收费标准如表所示:
(1)某用户四月份用水量为16吨,需交水费多少元?
(2)某用户五月份交水费60元,用水量为多少吨?
月用水量
不超过12吨的部分
超过12吨的部分且
不超过18吨的部分
超过18吨的部分
收费标准
2元/吨
2.5元/吨
3元/吨
解析
(1)∵12<16<18
(2)设五月份所用水量为x吨,由题意得
答:四月份需交水费34元。
答:五月份用水量为25吨。
x=25
2×12+6×2.5+(x-18)×3=60
∴2×12+2.5×(16-12)=34(元)
一元一次方程的应用——形积变化问题
将一个底面半径为6cm、高为40cm的“瘦长”圆柱形钢材锻压成底面半径为12cm的“矮胖”圆柱形零件毛坯,请问毛坯的高是多少?
解析
举一反三
有一根钢管长12米,要锯成两段,使第一段比第二段短2米,每段各长多少米?
解:设第二段长为x米,则第一段长为(x-2)米,由题意得:
x+(x-2)=12
解得x=7
则7-2=5(米)
答:第一段长5米,第二段长7米。
解:设毛坯的高为xcm,由题意得:
π×
×40
=π×
×x
x
=
10
答:毛坯的高是10cm。
一元一次方程的应用——打折销售问题
解析
举一反三
某服装进货价为80元/件,标价为200元/件,商店将此服装打x折销售后仍获利50%,则x为(
)
A.5
B.6
C.7
D.8
解:设最低打x折出售此商品,由题意得:
x
=
7
答:打7折出售此商品。
某商品进价为400元,标价为600元,商店要求以利润率不低于5%的售价打折出售,最低可以打几折出售此商品?
B
一元一次方程的应用——含两个等量关系的问题
某足球赛即将举行,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为5800元。
其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?
解析
解:设小李预定了小组赛球票x张,则
小组赛球票
淘汰赛球票
票数/张
x
票款/元
小组赛票款
+
淘汰赛票款
=
5800元
10-x
550x
700(10-x)
550x+700(10-x)=
5800
x
=
8
则10-x
=
10-8
=
2(张)
答:小李预定了小组赛球票8张,淘汰赛球票2张。
举一反三
某车间原计划13小时生产一批零件,实际每小时多生产了10件,用了12小时不但完成了任务,而且还多生产了60件,设原计划每小时生产x个零件,那么下列方程正确的是(
)
A.
13x=12(x+10)+60
B.
12(x+10)=13x+60
C.
D.
B
一元一次方程的应用——行程问题
运动场环形跑道周长400m,小红跑步的速度是爷爷的
倍,他们从同一起点沿跑道的同一方向同时出发,5min后小红第一次与爷爷相遇,小红和爷爷跑步的速度各是多少?
解析
速度/(m/min)
时间/min
路程/m
爷爷
x
小红
小红跑的路程
爷爷跑的路程
400m
解:设爷爷跑步的速度为xm/min,则小红跑步的速度为
m/min
x=120
答:爷爷跑步的速度为120m/min,则小红跑步的速度为200m/min.
5
5
5x
一元一次方程的应用——本息问题
王大伯3年前把手头一笔钱作为3年定期存款存入银行,年利率为5%,到期后得到本息共23000元,问当年王大伯存入银行多少钱?
解:设当年王大伯存入银行x元,由题意得
x+3×5%x
=
23000
解得
x
=
20000
解析
答:当年王大伯存入银行20000元.
利息=本金×利率×年数
本息和=本金+利息
=本金×(1+利率×期数)
举一反三
王先生到银行存了一笔三年期的
定期存款,年利率是4.25%,若到期后取出得到本息和(本金+利息)33825元。设王先生存入的本金为x元,则下面所列方程正确的是(
)
A.x+3×4.25%x=33825
B.x+4.25%x=33825
C.3×4.25%x=33825
D.3(x+4.25%x)=33825
A
一元一次方程的应用——工程问题
刺绣一件作品,甲单独绣需要15天完成,乙单独绣需要12天完成。现在甲先单独绣1天,接着乙又单独绣4天,剩下的工作由甲、乙两人合绣。问再绣多少天可以完成这件作品?
解析
解:设再绣x天可以完成这件作品,由题意得
解得
x=4
答:再绣4天可以完成这件作品。
用整体“1”表示总工作量!
工作量
=
工作效率×工作时间
路程
=
速度
×
时间
一元一次方程的应用——古代数学问题
《九章算术》中有“盈不足术”的问题,原文如下:“今有共買羊,人出五,不足四十五;人出七,不足三。问人数、羊價各幾何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元。问:人数和羊价各是多少?
解析
解:设买羊人数为x人,则羊的单价为(5x+45)元,由题意得
5x+45
=
7x+3
x
=
21
故5×21+45=150(元)
答:买羊人数为21人,羊的单价为150元.
举一反三
明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:所分的银子共有(
)两。(注:明代时1斤=16两,故有“半斤八两”这个成语)
46
一元一次方程的应用——顺水(逆水)问题
一艘船从甲码头到乙码头顺流行驶,用了2h,从乙码头返回甲码头逆流形式比顺流行驶多用了0.5h,已知水流的速度是3km/h,则船在静水中的速度是多少?
解析
解:设船在静水中的速度是xkm/h,则顺流时的速度为(x+3)km/h,逆流时的速度为(x-3)km/h,由题意得
2(x+3)=
2.5(x-3)
x
=
27
答:船在静水中的速度是27km/h。
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
举一反三
一艘轮船在A,B两港口之间行驶,顺水航行需要5h,逆水航行需要7h,水流的速度是5km/h,则A,B两港口之间的路程是(
)
A.105km
B.175km
C.180km
D.210km
B
一元一次方程的应用——周长问题
一个长方形的周长为30cm,若这个长方形的长减少1cm,宽增加2cm就可成为一个正方形,设长方形的长为xcm,可列方程为(
)
解析
举一反三
1.某小区在规划设计时,准备在两栋楼房之间设置一块周长为120米的长方形绿地,并且长比宽多10米。设绿地的宽为x米,根据题意,列出的方程是(
)
2.如右图,在周长为10m的长方形窗户上钉一块宽为1m的长方形遮阳布,使透光部分正好是一正方形,则定钉好后透光面积为(
)
(第2题图)
2[x+(x+10)]=120
4平方米
x-1=(15-x)+2
x
15-x
x-1
(15-x)+2
(长+宽)×2=周长
(长+宽)=周长÷2
一元一次方程的应用——面积问题
如图,小红将一个正方形纸片剪去一个宽为4厘米的长条后,再从剩下的长方形纸片上剪去一个宽为5厘米的长条,且剪下的两个长条的面积相等。正方形的边长为多少厘米?设正方形的边长为x厘米,则可列方程_____________________,解方程可知正方形的边长为_____________厘米。
解析
5cm
4cm
举一反三
在梯形面积公式
中,已知h=6厘米,a=3厘米,S=24平方厘米,则b等于(
)
A.1厘米
B.5厘米
C.3厘米
D.4厘米
B
4x=5(x-4)
20
xcm
(x-4)cm
4x=5(x-4)
4x=5x-20
20=5x-4x
x=20
一元一次方程的应用——等积变换问题
如图,在水平桌面上有甲、乙两个内部呈圆柱形、高度相同的容器,内部底面积分别为80平方厘米,100平方厘米,且甲容器装满水,乙容器是空的,若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲中的水位高度低了8cm,则甲的容积为(
)
解析
举一反三
有一个长、宽、高分别是15cm,10cm,30cm的长方体钢锭,现将它锻压成一个底面为正方形,且边长为15cm的长方体钢锭,高变成了__________.
甲
乙
乙
8cm
xcm
圆柱体积
=
底面积
×
高
x
=
40
40×80=3200立方厘米
20cm
一元一次方程的应用——比例问题
某中学在“献爱心”活动中,六年级五个班共捐款6300元,其中一班捐款1400元,二班比一班少捐款100元,三班捐款数是年级总数的20%,四班与五班捐款数之比是6:7.求四班捐款多少元?
解析
举一反三
一个三角形的三条边的长度之比为2:4:5,最长的边比最短的边长6cm,求该三角形的周长。
四班与五班捐款的总数:6300-1400-(1400-100)-6300×20%=2340(元)
设四班捐款为6x元,五班捐款为7x元,
6x+7x=2340
x=180,则6x=1080
22cm
一班:1400元
二班:1400-100
三班:6300×20%
一元一次方程的应用——阶梯计费问题
某城市自来水收费实行阶梯水价,收费标准如表所示:
(1)某用户四月份用水量为16吨,需交水费多少元?
(2)某用户五月份交水费60元,用水量为多少吨?
月用水量
不超过12吨的部分
超过12吨的部分且
不超过18吨的部分
超过18吨的部分
收费标准
2元/吨
2.5元/吨
3元/吨
解析
(1)∵12<16<18
(2)设五月份所用水量为x吨,由题意得
答:四月份需交水费34元。
答:五月份用水量为25吨。
x=25
2×12+6×2.5+(x-18)×3=60
∴2×12+2.5×(16-12)=34(元)
