鲁教版五四制六年级数学上册3.6 :整式的加减 教学课件共19张PPT
文档属性
| 名称 | 鲁教版五四制六年级数学上册3.6 :整式的加减 教学课件共19张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 499.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 08:14:34 | ||
图片预览






文档简介
(共19张PPT)
3.6
整式的加减
1判断是否是同类项,若是请合并同类项
(1)3a2b3
与-a3b2
(2)
(3)3与-2
(4)abc与ab
不是
不是
是
是
复习回顾:
1
2.去括号:
(5)+(3x-3)
=
3x-3
-x+1
-4x+6y
-3ab+6a
(6)-(x-1)
=
(7)3(-
ab+2a)=
(8)-2(2x-3y)=
按照下面的步骤做:
(1)任意写一个两位数;
(2)交换这个两位数的十位数字和个位数字的位置,又得到一个新的两位数;
(3)求这两个数的和.
合作探究:
(4)
小组交流“和”有规律么?这个规律对于任意一个两位数都成立么?
如果设十位数字为a个位数字为b,则这个两位数表示为
,交换位置则新的两位数表示
;
——规律:11的倍数.
(10a+b)+(10b+a)
=10a+b+10b+a
=11a+11b
=11(a+b)
10a+b
10b+a
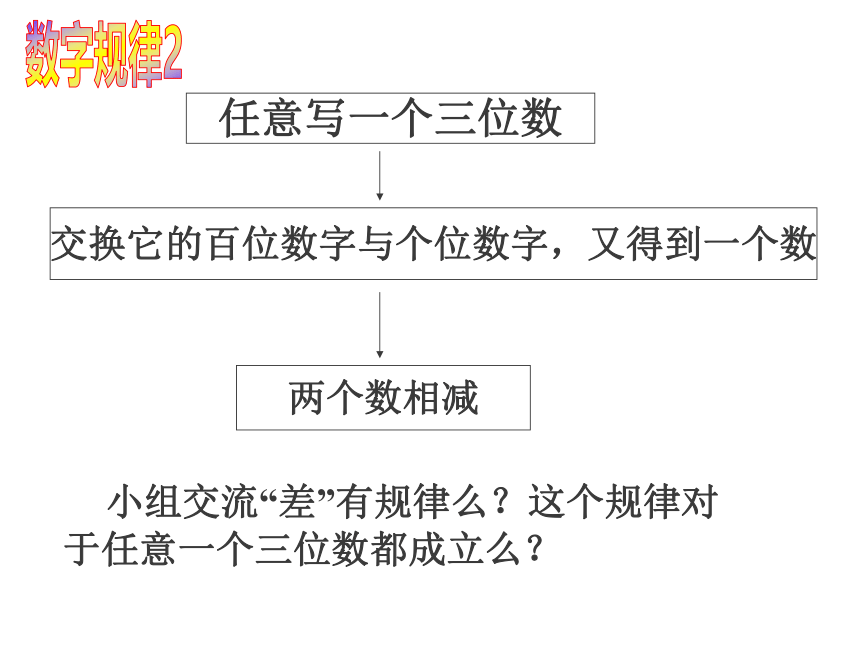
任意写一个三位数
交换它的百位数字与个位数字,又得到一个数
两个数相减
小组交流“差”有规律么?这个规律对于任意一个三位数都成立么?
如果设三位数的百位为a,十位为b,个位为c则这三位数表示
,
百位数字与个位数字交换后的新三位数为
,它们的差为:
100a+10b+c
100c+10b+a
(
100a+10b+c)-(
100c+10b+a)
=
100a+10b+c-100c-10b-a
=99a-99c
=99(a-c)
——规律:99的倍数.
议一议
在上面两个问题中,分别涉及了整式的什么运算?说一说你是如何运算的?
进行整式加减运算时,如果遇到括号要先去括号,再合并同类项.
例1
计算:
(1)
与
的和;
例题赏析:
(2)
与
的差;
解:(1)
解:(2)
基础达标
变式训练
能力提升
跟踪训练:
基础达标
变式训练
已知
求
能力提升
多项式
与多项
式
的差不含二次项,求m
的值?
=
=
由题意得
解:
法一:
法二:
解:由题意得
=
学习就像登山一样,需要努力,需要坚持,虽然过程中会有艰难,但只要学会享受,便能乐在其中,希望同学们能奋力拼搏,登上峰顶,饱览美景!
同学们,今天你有什么收获?
课堂小结:
1、
2、求多项式
与多项
式
的差。
★选做题:
当堂达标:
(
)
作业:
必做:《伴你学》基础演练
选做:自己设计一个数字规律游
戏,并用整式的加减运算说明其
中的规律。
3.6
整式的加减
1判断是否是同类项,若是请合并同类项
(1)3a2b3
与-a3b2
(2)
(3)3与-2
(4)abc与ab
不是
不是
是
是
复习回顾:
1
2.去括号:
(5)+(3x-3)
=
3x-3
-x+1
-4x+6y
-3ab+6a
(6)-(x-1)
=
(7)3(-
ab+2a)=
(8)-2(2x-3y)=
按照下面的步骤做:
(1)任意写一个两位数;
(2)交换这个两位数的十位数字和个位数字的位置,又得到一个新的两位数;
(3)求这两个数的和.
合作探究:
(4)
小组交流“和”有规律么?这个规律对于任意一个两位数都成立么?
如果设十位数字为a个位数字为b,则这个两位数表示为
,交换位置则新的两位数表示
;
——规律:11的倍数.
(10a+b)+(10b+a)
=10a+b+10b+a
=11a+11b
=11(a+b)
10a+b
10b+a
任意写一个三位数
交换它的百位数字与个位数字,又得到一个数
两个数相减
小组交流“差”有规律么?这个规律对于任意一个三位数都成立么?
如果设三位数的百位为a,十位为b,个位为c则这三位数表示
,
百位数字与个位数字交换后的新三位数为
,它们的差为:
100a+10b+c
100c+10b+a
(
100a+10b+c)-(
100c+10b+a)
=
100a+10b+c-100c-10b-a
=99a-99c
=99(a-c)
——规律:99的倍数.
议一议
在上面两个问题中,分别涉及了整式的什么运算?说一说你是如何运算的?
进行整式加减运算时,如果遇到括号要先去括号,再合并同类项.
例1
计算:
(1)
与
的和;
例题赏析:
(2)
与
的差;
解:(1)
解:(2)
基础达标
变式训练
能力提升
跟踪训练:
基础达标
变式训练
已知
求
能力提升
多项式
与多项
式
的差不含二次项,求m
的值?
=
=
由题意得
解:
法一:
法二:
解:由题意得
=
学习就像登山一样,需要努力,需要坚持,虽然过程中会有艰难,但只要学会享受,便能乐在其中,希望同学们能奋力拼搏,登上峰顶,饱览美景!
同学们,今天你有什么收获?
课堂小结:
1、
2、求多项式
与多项
式
的差。
★选做题:
当堂达标:
(
)
作业:
必做:《伴你学》基础演练
选做:自己设计一个数字规律游
戏,并用整式的加减运算说明其
中的规律。
