鲁教版(五四制)六年级上册4.2 解一元一次方程(第二课时)课件
文档属性
| 名称 | 鲁教版(五四制)六年级上册4.2 解一元一次方程(第二课时)课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 08:13:26 | ||
图片预览






文档简介
(共16张PPT)
4.2 解一元一次方程(第二课时)
---去括号
学习目标
能熟练运用去括号法则,乘法分配律去括号后解 一元一次方程。
如果设1听果奶x元,
根据等量关系:买果奶钱数+买可乐钱数=(20-3)元
可列方程为:
4(x+0.5)+x=20-3
1、所列方程与上节课所学方程有什么区别?
想一想
2、怎样解所列的方程吗?
(
(
去括号转化为没有括号的方程再进一步化成x=a的形式
去括号:
方程中的去括号法则与整式运算中的去括号法则相同
去括号,看符号
是“+”,不变号
是“-”,全变号
+
解:去括号,得
a-2b+c
解:去括号,得
2x-3y+7
当括号前是“+1”或“-1”时
例1 将下列各式去括号
(1)(a-2b+c) (2)-(-2x+3y-7)
-
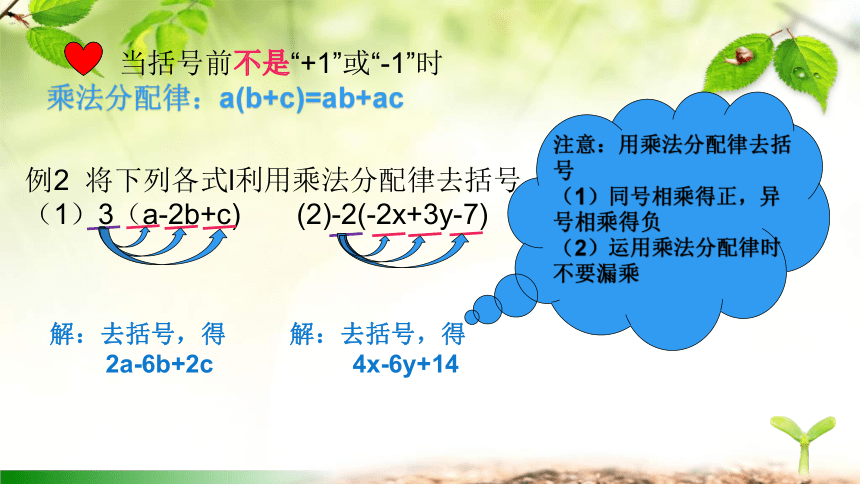
例2 将下列各式l利用乘法分配律去括号
(1)3(a-2b+c) (2)-2(-2x+3y-7)
解:去括号,得
2a-6b+2c
解:去括号,得
4x-6y+14
当括号前不是“+1”或“-1”时
乘法分配律:a(b+c)=ab+ac
注意:用乘法分配律去括号
(1)同号相乘得正,异号相乘得负
(2)运用乘法分配律时不要漏乘
练习
将下列式子去括号
(1) 2(3x-5) (2) -3(-x+4)
(3) 8y-3(3y-2) (4) 2(x+8)-3(x-1)
解:去括号,得 6x-10
解:去括号,得2x+16-3x=3
解:去括号,得8y-9y+6
解:去括号,得3x-12
解方程:4(x+0.5)+x=17
解:去括号,得:4x+2+x=17
移项,得:4x+x=17-2
合并同类项,得:5x=15
方程两边同除以5,得:x=3
解有括号一元一次方程的一般步骤
系数化一
——
————
——
————
知识应用
例题学习
例3:解方程:-2(x-1)=4
解法一:去括号,得:-2x+2=4
移项,得:-2x=4-2
合并同类项,得:-2x=2
系数化1,得:x=-1
括号前是负因数每项要变号
例题学习
例3:解方程:-2(x-1)=4
解法二:方程两边同除以-2,得:
X-1=-2
移项,得:x=-2+1
合并同类项,得:x=-1
体会与总结:
这里把“x-1”看作一个整体,根据等式的
基本性质2,同样可以把括号去掉。
这也是数学经常用到的“整体思想”
知识拓展
试试你的能力
去括号的顺序:
多重括号先去那个括号呢?
一般先去小括号,再去中括号,最后去大括号,也就是由内向外
具体由外向内去括号还是由内向外去括号也要因题而异。
也可以先去大括号,再去中括号,最后去小括号,也就是由外向内
为减少移项的项数先合并同类项,再进行移项
知识拓展
试试你的能力
课堂小结
去括号法则:若括号外的因数是正数时去括后式子各项不变号。若括号外的因数是负数时去括后式子各项都变号
解有括号一元一次方程的一般步骤:
1、去括号 2、移项 3、合并同类项 4、系数化一
去括号的顺序:可以由内向外也可以有外向内因题而异。
当堂检测
1、下列解方程过程有几处错误,找出并改正。
3(3x-7)-2(1+x)=6
去括号,得:9x-7-2+2x=6
移项,得 :9x+2x=7+2-6
2、解下列方程
(1)10(x-1)=5
(2)3(x+1)-2(x+2)=2x+3
同学们!再见!
一分耕耘,一分收获,未必;
九分耕耘,会有收获,一定!
4.2 解一元一次方程(第二课时)
---去括号
学习目标
能熟练运用去括号法则,乘法分配律去括号后解 一元一次方程。
如果设1听果奶x元,
根据等量关系:买果奶钱数+买可乐钱数=(20-3)元
可列方程为:
4(x+0.5)+x=20-3
1、所列方程与上节课所学方程有什么区别?
想一想
2、怎样解所列的方程吗?
(
(
去括号转化为没有括号的方程再进一步化成x=a的形式
去括号:
方程中的去括号法则与整式运算中的去括号法则相同
去括号,看符号
是“+”,不变号
是“-”,全变号
+
解:去括号,得
a-2b+c
解:去括号,得
2x-3y+7
当括号前是“+1”或“-1”时
例1 将下列各式去括号
(1)(a-2b+c) (2)-(-2x+3y-7)
-
例2 将下列各式l利用乘法分配律去括号
(1)3(a-2b+c) (2)-2(-2x+3y-7)
解:去括号,得
2a-6b+2c
解:去括号,得
4x-6y+14
当括号前不是“+1”或“-1”时
乘法分配律:a(b+c)=ab+ac
注意:用乘法分配律去括号
(1)同号相乘得正,异号相乘得负
(2)运用乘法分配律时不要漏乘
练习
将下列式子去括号
(1) 2(3x-5) (2) -3(-x+4)
(3) 8y-3(3y-2) (4) 2(x+8)-3(x-1)
解:去括号,得 6x-10
解:去括号,得2x+16-3x=3
解:去括号,得8y-9y+6
解:去括号,得3x-12
解方程:4(x+0.5)+x=17
解:去括号,得:4x+2+x=17
移项,得:4x+x=17-2
合并同类项,得:5x=15
方程两边同除以5,得:x=3
解有括号一元一次方程的一般步骤
系数化一
——
————
——
————
知识应用
例题学习
例3:解方程:-2(x-1)=4
解法一:去括号,得:-2x+2=4
移项,得:-2x=4-2
合并同类项,得:-2x=2
系数化1,得:x=-1
括号前是负因数每项要变号
例题学习
例3:解方程:-2(x-1)=4
解法二:方程两边同除以-2,得:
X-1=-2
移项,得:x=-2+1
合并同类项,得:x=-1
体会与总结:
这里把“x-1”看作一个整体,根据等式的
基本性质2,同样可以把括号去掉。
这也是数学经常用到的“整体思想”
知识拓展
试试你的能力
去括号的顺序:
多重括号先去那个括号呢?
一般先去小括号,再去中括号,最后去大括号,也就是由内向外
具体由外向内去括号还是由内向外去括号也要因题而异。
也可以先去大括号,再去中括号,最后去小括号,也就是由外向内
为减少移项的项数先合并同类项,再进行移项
知识拓展
试试你的能力
课堂小结
去括号法则:若括号外的因数是正数时去括后式子各项不变号。若括号外的因数是负数时去括后式子各项都变号
解有括号一元一次方程的一般步骤:
1、去括号 2、移项 3、合并同类项 4、系数化一
去括号的顺序:可以由内向外也可以有外向内因题而异。
当堂检测
1、下列解方程过程有几处错误,找出并改正。
3(3x-7)-2(1+x)=6
去括号,得:9x-7-2+2x=6
移项,得 :9x+2x=7+2-6
2、解下列方程
(1)10(x-1)=5
(2)3(x+1)-2(x+2)=2x+3
同学们!再见!
一分耕耘,一分收获,未必;
九分耕耘,会有收获,一定!
