鲁教版(五四制)六年级数学上册:4.2 解一元一次方程 课件(共48张PPT)
文档属性
| 名称 | 鲁教版(五四制)六年级数学上册:4.2 解一元一次方程 课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览





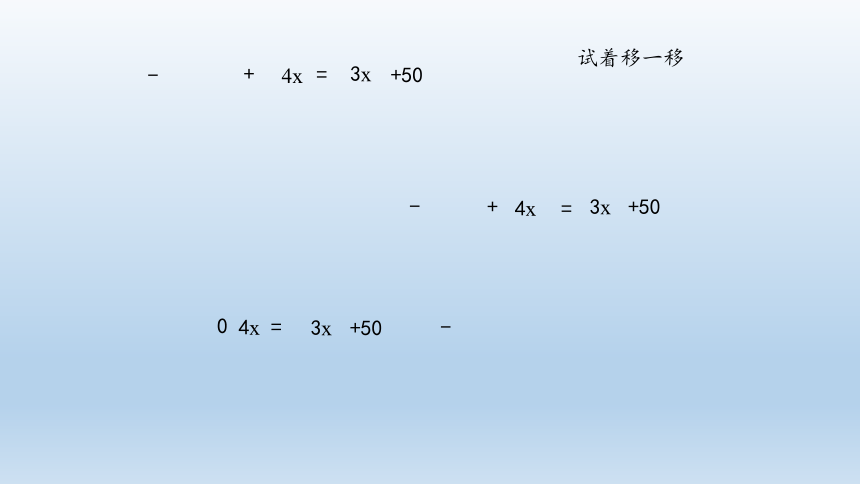




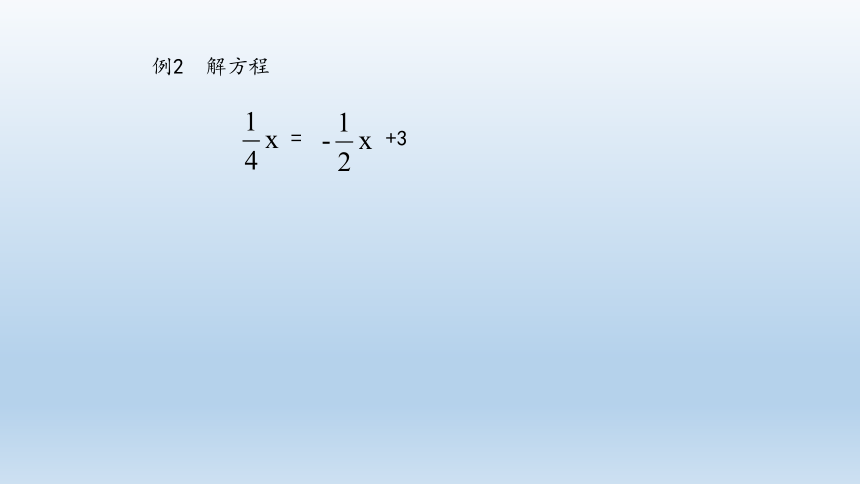

文档简介
(共48张PPT)
第一课时
解一元一次方程
教学目标
1、理解、掌握移项的概念。
2、运用移项解决简单的一元一次方程问题。
知识回顾
什么叫一元一次方程?
等式的两个性质:
1、等式的两边都加上或减去同一个代数式,所得结果仍是等式。
2、等式的两边都乘以或除以同一个不为零的数,所得结果仍是等式。
(1)你能运用等式的基本性质解方程x-2=5吗?与同学交流。
方程x-2=5的两边都加上2,得
x=5+2
探索新知
即x=7
-2
+2
4x-3x=
50
你会解吗?
4x=
3x+50
4x-3x=3x+50
-3x
x=50
注意:移项要变号!
比较:这两个方程
发生了什么变化
一般地,把方程中的项改变符号后,
从方程的一边移到另一边,这种变形
叫做移项(transposition
of
terms)。
(等式性质1)
=
3x
+50
4x
=
3x
+50
4x
=
3x
+50
4x
-
+
-
+
-
0
试着移一移
(1)6+x=8,移项得
x
=8+6。
(2)3x=8-2x,移项得3x+2x=-8。
(3)5x-2=3x+7,移项得5x+3x=7+2。
错
x=8-6
错
3x+2x=8
错
5x-3x=7+2
慧眼找错
移项时应注意改变项的符号
将含未知数的项放在方程的一边,常数项放在方程的另一边,对方程进行移项变形。
(2)
5x=3x-1
(1)
2x-3=
6
(3)
2.4y+2=-2y
(4)
8-5x=x+2
2x
=6+3
5x-3x=-1
2.4y+2y
=-2
-5x-x=2-8
抢答
例1
解方程:2x+6=1
每一步变形的依据是什么?
只要设法将未知数的系数化为1
就行了。
解方程:3x+3=2x+7
1、一般把含有未知数的项移到等号左边,常数项移到等号右边。
2、移项记得要变号。
例题解析
巩固练习
解方程:
(1)x-3=-12;
(2)5-2x=9-3x;
(3)16x+6=-7+15x;
(4)3y-2=2y-10。
例2 解方程
=
+3
下面方程的解法对吗?如果不对,应怎样改正?
解方程:
移项,得
合并同类项,得
系数化为1,得
一起来找茬:
巩固练习
随堂练习(3)(4),习题1中的(3)(4)。
请同学们回顾一下,这节课你学到了什么?
把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
第二课时
解一元一次方程
1听果奶多少钱?
如果设1听果奶x
元,可列出方程:
4(x+0.5)+x=20-3
情景引入
教学目标
1、掌握解一元一次方程的基本方法:去括号。
2、能熟练求解数字系数的一元一次方程。
3、能根据实际情况列方程、解方程。
知识回顾:
①
解方程移项时,含有未知数的项、常数项分别移往等号哪边?
②
移项后的化简包括哪些内容?
含未知数的移到等号的左边、常数项移到等号的右边。
左边对含未知数的项合并、右边对常数项合并。并把未知项的系数化为1,形如x=ɑ(ɑ为常数)。
解方程:
4(x+0.5)+x=17
此方程与上课时所学方程有何差异?
需要先去括号。
去括号有什么注意事项呢?
观察分析
例3
此方程该如何解呢?
1、去括号;
2、移项;
3、合并同类项;
4、系数化为1。
解方程:
试一试
解:去括号,得:
移项,得:
合并同类项,得:
系数化为1,得:
例4
解方程:
-2(x-1)=4
你有几种方法呢?
方法一:先去括号。
方法二:整体思想。
2.解方程2(x-2)-3(4x-1)=9正确的是(
)
ɑ.2x-4-12x+3=9,-10x=8,故x=-0.8
B.2x-4-12x+3=9,-10x=10,故x=-1
C.2x-4-12x-3=9,-10x=16,故x=-1.6
D.2x-2-12x+1=9,-10x=10,故x=-1
1.对于方程2(2x-1)-(x-3)=1,去括号正确的是(
)
ɑ.4x-1-x-3=1
B.4x-1-x+3=1
C.4x-2-x-3=1
D.4x-2-x+3=1
B
巩固练习
D
3.方程2(x+1)=
的解是(
)
ɑ.x=-
B.x=
C.x=-
D.x=
C
4.在解方程4(2x+3)=8(1-x)-5(x-2)时,去括号后的
结果是
。
5.解下列方程:
(1)4(x-2)=3(1+3x)-12
(2)2(2x+1)-(x+5)-2(x-32)=2x+1
8x+12=8-8x-5x+10
本节课你的收获是什么?
1、这节课我们会了解怎样一元一次方程?
注意:
①移项时一定要变符号。
②去括号时务必看清括号前有无非1的系数、有无负号。
带有括号的方程。
2、解带有括号的方程的步骤是什么?
先去括号、再移项、合并同类项、最后系数化为1。
第三课时
解一元一次方程
知识回顾:
1、我们已经学过解一元一次方程的步骤有哪些?
2、解方程12(x+1)=
-(3x-1)。
3、你会解这个方程
吗?
教学目标
1、掌握解一元一次方程的基本方法:去分母。
2、熟练掌握解一元一次方程的基本步骤。
解方程:
去分母时要注意什么问题?
(1)方程两边每一项都要乘以各分母的最小公倍数。
(2)去分母后如分子中含有两项,应将该分子添上括号。
想一想:
你有几种解法?相互交流。
典型例析
例5
试一试
解方程:
解一元一次方程的步骤:
1、去分母;
2、去括号;
3、移项;
4、合并同类项;
5、系数化为1。
例
6
解方程:
指出解方程
2
x-1
5
4x+2
=
-2(x-1)
过程中
所有的错误,并加以改正。
解:
去分母,得
5
x-1
=
2(4x+2)
–
2
(x-1)
去括号,得
5x-1=8x+4-2x-2
移项,得
8x+5x+2x=4-2+1
合并同类项,得
15x
=3
系数化为1,得
x
=5
(
)
找一找错在哪里?
解下列方程:
练一练
(1)
(2)
去分母时须注意:
1、确定分母的最小公倍数;
2、不要漏乘没有分母的项;
3、去掉分母后,若分子是多项式,应把多项式(分子)添上括号,视多项式为一整体。
归纳:
解一元一次方程的一般步骤
变形名称
注意事项
去分母
去括号
移项
合并同类项
系数化为1
防止漏乘(尤其没有分母的项),注意添括号;
注意符号,防止漏乘;
移项要变号,防止漏项;
系数为1或-1时,记得省略1;
分子、分母不要写倒了;
这节课你学到了什么?有何收获?
1、解一元一次方程的步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1。
2、解方程的五个步骤在解题时不一定都需要,可根据题意灵活选用。
3、去分母时不要忘记添括号,不漏乘不含分母的项。
特别关注
1、去分母时,应在方程的左右两边都乘以分母
的最小公倍数,不能漏乘没有分母的项。
2、括号前是负号的去掉括号时,括号内各项都要变号。
3、移项是从方程的一边移到另一边,必须变号;只在方程一边交换位置的项不变号。
4、合并同类项时,系数加、减要细心。
5、系数化为1时,要注意负号与分数。
6、求出解后养成检验的习惯。
第四课时
解一元一次方程
解一元一次方程的一般步骤
变形名称
注意事项
去分母
去括号
移项
合并同类项
系数化为1
防止漏乘(尤其没有分母的项),注意添括号;
注意符号,防止漏乘;
移项要变号,防止漏项;
系数为1或-1时,记得省略1;
分子、分母不要写倒了;
知识回顾:
教学目标
1、理解并掌握小数分母化成整数分母的理论依据。
2、熟练掌握解一元一次方程的基本步骤。
3、会解稍复杂的一元一次方程。
例7
解方程:
你有几种解法?相互交流。
(1)解方程的过程就是通过去分母、去括号、移项、合并同类项、(未知数)系数化为1等步骤,把一个一元一次方程逐步转化为x=ɑ的形式.这是一个等量变形的过程,也是一个化归的过程。(转化的思想)
(2)具体解方程时,可根据具体情况,有些步骤可能用不上;有些步骤可以前后顺序颠倒;有时还可以省略一些步骤,以使运算简化。
试一试
解方程
1、
2、
例8
解方程:
注意:(易错点)将小数分母化成整数分母,其理论根据不是等式的基本性质,而是分数的性质,是含小数的项的分子、分母都乘以同一个适当的数,而不是方程两边所有的项同乘这个数。
练一练
解方程
步骤
具体做法
依据
注意事项
小数分母化
整数分母
分子分母同乘一个适当的数
分数的性质
不是方程两边所有的项都乘
去分母
在方程的两边都乘各分母的最小公倍数
等式性质2
不要漏乘不含分母的项,分子是多项式时别忘加括号。
去括号
先去小括号,再去中括号,最后去大括号
乘法分配律
去括号法则
括号前是“-”时,去掉括号时括号内各项均要变号
移项
将含未知数的项移到方程的一边,常数项移到方程的另一边
移项法则
移项要变号
合并同类项
找到同类项合并
合并同类项法则
系数相加,字母及字母的指数均不变
系数化为1
把方程的两边都除以未知数的系数(不为0)
等式性质2
分子、分母不要颠倒
归纳:
这节课你学到了什么?有何收获?
1、解一元一次方程的步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1。
2、解方程的五个步骤在解题时不一定都需要,可根据题意灵活选用。
3、将小数分母化成整数分母,其理论根据不是等式的基本性质,而是分数的性质,是含小数的项的分子、分母都乘以同一个适当的数,而不是方程两边所有的项同乘这个数。
谢
谢
第一课时
解一元一次方程
教学目标
1、理解、掌握移项的概念。
2、运用移项解决简单的一元一次方程问题。
知识回顾
什么叫一元一次方程?
等式的两个性质:
1、等式的两边都加上或减去同一个代数式,所得结果仍是等式。
2、等式的两边都乘以或除以同一个不为零的数,所得结果仍是等式。
(1)你能运用等式的基本性质解方程x-2=5吗?与同学交流。
方程x-2=5的两边都加上2,得
x=5+2
探索新知
即x=7
-2
+2
4x-3x=
50
你会解吗?
4x=
3x+50
4x-3x=3x+50
-3x
x=50
注意:移项要变号!
比较:这两个方程
发生了什么变化
一般地,把方程中的项改变符号后,
从方程的一边移到另一边,这种变形
叫做移项(transposition
of
terms)。
(等式性质1)
=
3x
+50
4x
=
3x
+50
4x
=
3x
+50
4x
-
+
-
+
-
0
试着移一移
(1)6+x=8,移项得
x
=8+6。
(2)3x=8-2x,移项得3x+2x=-8。
(3)5x-2=3x+7,移项得5x+3x=7+2。
错
x=8-6
错
3x+2x=8
错
5x-3x=7+2
慧眼找错
移项时应注意改变项的符号
将含未知数的项放在方程的一边,常数项放在方程的另一边,对方程进行移项变形。
(2)
5x=3x-1
(1)
2x-3=
6
(3)
2.4y+2=-2y
(4)
8-5x=x+2
2x
=6+3
5x-3x=-1
2.4y+2y
=-2
-5x-x=2-8
抢答
例1
解方程:2x+6=1
每一步变形的依据是什么?
只要设法将未知数的系数化为1
就行了。
解方程:3x+3=2x+7
1、一般把含有未知数的项移到等号左边,常数项移到等号右边。
2、移项记得要变号。
例题解析
巩固练习
解方程:
(1)x-3=-12;
(2)5-2x=9-3x;
(3)16x+6=-7+15x;
(4)3y-2=2y-10。
例2 解方程
=
+3
下面方程的解法对吗?如果不对,应怎样改正?
解方程:
移项,得
合并同类项,得
系数化为1,得
一起来找茬:
巩固练习
随堂练习(3)(4),习题1中的(3)(4)。
请同学们回顾一下,这节课你学到了什么?
把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
第二课时
解一元一次方程
1听果奶多少钱?
如果设1听果奶x
元,可列出方程:
4(x+0.5)+x=20-3
情景引入
教学目标
1、掌握解一元一次方程的基本方法:去括号。
2、能熟练求解数字系数的一元一次方程。
3、能根据实际情况列方程、解方程。
知识回顾:
①
解方程移项时,含有未知数的项、常数项分别移往等号哪边?
②
移项后的化简包括哪些内容?
含未知数的移到等号的左边、常数项移到等号的右边。
左边对含未知数的项合并、右边对常数项合并。并把未知项的系数化为1,形如x=ɑ(ɑ为常数)。
解方程:
4(x+0.5)+x=17
此方程与上课时所学方程有何差异?
需要先去括号。
去括号有什么注意事项呢?
观察分析
例3
此方程该如何解呢?
1、去括号;
2、移项;
3、合并同类项;
4、系数化为1。
解方程:
试一试
解:去括号,得:
移项,得:
合并同类项,得:
系数化为1,得:
例4
解方程:
-2(x-1)=4
你有几种方法呢?
方法一:先去括号。
方法二:整体思想。
2.解方程2(x-2)-3(4x-1)=9正确的是(
)
ɑ.2x-4-12x+3=9,-10x=8,故x=-0.8
B.2x-4-12x+3=9,-10x=10,故x=-1
C.2x-4-12x-3=9,-10x=16,故x=-1.6
D.2x-2-12x+1=9,-10x=10,故x=-1
1.对于方程2(2x-1)-(x-3)=1,去括号正确的是(
)
ɑ.4x-1-x-3=1
B.4x-1-x+3=1
C.4x-2-x-3=1
D.4x-2-x+3=1
B
巩固练习
D
3.方程2(x+1)=
的解是(
)
ɑ.x=-
B.x=
C.x=-
D.x=
C
4.在解方程4(2x+3)=8(1-x)-5(x-2)时,去括号后的
结果是
。
5.解下列方程:
(1)4(x-2)=3(1+3x)-12
(2)2(2x+1)-(x+5)-2(x-32)=2x+1
8x+12=8-8x-5x+10
本节课你的收获是什么?
1、这节课我们会了解怎样一元一次方程?
注意:
①移项时一定要变符号。
②去括号时务必看清括号前有无非1的系数、有无负号。
带有括号的方程。
2、解带有括号的方程的步骤是什么?
先去括号、再移项、合并同类项、最后系数化为1。
第三课时
解一元一次方程
知识回顾:
1、我们已经学过解一元一次方程的步骤有哪些?
2、解方程12(x+1)=
-(3x-1)。
3、你会解这个方程
吗?
教学目标
1、掌握解一元一次方程的基本方法:去分母。
2、熟练掌握解一元一次方程的基本步骤。
解方程:
去分母时要注意什么问题?
(1)方程两边每一项都要乘以各分母的最小公倍数。
(2)去分母后如分子中含有两项,应将该分子添上括号。
想一想:
你有几种解法?相互交流。
典型例析
例5
试一试
解方程:
解一元一次方程的步骤:
1、去分母;
2、去括号;
3、移项;
4、合并同类项;
5、系数化为1。
例
6
解方程:
指出解方程
2
x-1
5
4x+2
=
-2(x-1)
过程中
所有的错误,并加以改正。
解:
去分母,得
5
x-1
=
2(4x+2)
–
2
(x-1)
去括号,得
5x-1=8x+4-2x-2
移项,得
8x+5x+2x=4-2+1
合并同类项,得
15x
=3
系数化为1,得
x
=5
(
)
找一找错在哪里?
解下列方程:
练一练
(1)
(2)
去分母时须注意:
1、确定分母的最小公倍数;
2、不要漏乘没有分母的项;
3、去掉分母后,若分子是多项式,应把多项式(分子)添上括号,视多项式为一整体。
归纳:
解一元一次方程的一般步骤
变形名称
注意事项
去分母
去括号
移项
合并同类项
系数化为1
防止漏乘(尤其没有分母的项),注意添括号;
注意符号,防止漏乘;
移项要变号,防止漏项;
系数为1或-1时,记得省略1;
分子、分母不要写倒了;
这节课你学到了什么?有何收获?
1、解一元一次方程的步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1。
2、解方程的五个步骤在解题时不一定都需要,可根据题意灵活选用。
3、去分母时不要忘记添括号,不漏乘不含分母的项。
特别关注
1、去分母时,应在方程的左右两边都乘以分母
的最小公倍数,不能漏乘没有分母的项。
2、括号前是负号的去掉括号时,括号内各项都要变号。
3、移项是从方程的一边移到另一边,必须变号;只在方程一边交换位置的项不变号。
4、合并同类项时,系数加、减要细心。
5、系数化为1时,要注意负号与分数。
6、求出解后养成检验的习惯。
第四课时
解一元一次方程
解一元一次方程的一般步骤
变形名称
注意事项
去分母
去括号
移项
合并同类项
系数化为1
防止漏乘(尤其没有分母的项),注意添括号;
注意符号,防止漏乘;
移项要变号,防止漏项;
系数为1或-1时,记得省略1;
分子、分母不要写倒了;
知识回顾:
教学目标
1、理解并掌握小数分母化成整数分母的理论依据。
2、熟练掌握解一元一次方程的基本步骤。
3、会解稍复杂的一元一次方程。
例7
解方程:
你有几种解法?相互交流。
(1)解方程的过程就是通过去分母、去括号、移项、合并同类项、(未知数)系数化为1等步骤,把一个一元一次方程逐步转化为x=ɑ的形式.这是一个等量变形的过程,也是一个化归的过程。(转化的思想)
(2)具体解方程时,可根据具体情况,有些步骤可能用不上;有些步骤可以前后顺序颠倒;有时还可以省略一些步骤,以使运算简化。
试一试
解方程
1、
2、
例8
解方程:
注意:(易错点)将小数分母化成整数分母,其理论根据不是等式的基本性质,而是分数的性质,是含小数的项的分子、分母都乘以同一个适当的数,而不是方程两边所有的项同乘这个数。
练一练
解方程
步骤
具体做法
依据
注意事项
小数分母化
整数分母
分子分母同乘一个适当的数
分数的性质
不是方程两边所有的项都乘
去分母
在方程的两边都乘各分母的最小公倍数
等式性质2
不要漏乘不含分母的项,分子是多项式时别忘加括号。
去括号
先去小括号,再去中括号,最后去大括号
乘法分配律
去括号法则
括号前是“-”时,去掉括号时括号内各项均要变号
移项
将含未知数的项移到方程的一边,常数项移到方程的另一边
移项法则
移项要变号
合并同类项
找到同类项合并
合并同类项法则
系数相加,字母及字母的指数均不变
系数化为1
把方程的两边都除以未知数的系数(不为0)
等式性质2
分子、分母不要颠倒
归纳:
这节课你学到了什么?有何收获?
1、解一元一次方程的步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1。
2、解方程的五个步骤在解题时不一定都需要,可根据题意灵活选用。
3、将小数分母化成整数分母,其理论根据不是等式的基本性质,而是分数的性质,是含小数的项的分子、分母都乘以同一个适当的数,而不是方程两边所有的项同乘这个数。
谢
谢
