2021年高考数学真题模拟试题专项汇编之概率与统计(文)(Word版,含解析)
文档属性
| 名称 | 2021年高考数学真题模拟试题专项汇编之概率与统计(文)(Word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 619.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 10:11:18 | ||
图片预览




文档简介
(11)概率与统计(文)——2021年高考数学真题模拟试题专项汇编
1.【2021年全国甲卷(文),2】为了解某地农村经济情况,对该地农户家庭年收入进行抽样调査,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是(
)
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
2.【2021年四川简阳模拟(文),3】霍兰德职业能力测试问卷可以为大学生在择业方面提供参考,对人的能力兴趣等方面进行评估.某大学随机抽取100名学生进行霍兰德职业能力测试问卷测试,测试结果发现这100名学生的得分都在内,按得分分成5组:,,,,,得到如图所示的频率分布直方图,则这100名同学得分的中位数为(
)
A.72.5
B.75
C.77.5
D.80
3.【2021年吉林长春模拟(文),4】党的十八大以来,我们在脱贫攻坚领域取得了前所未有的成就,农村贫困人口大幅减少,解决困扰中华民族几千年的贫困问题,取得历史性成就.
同时为全球减贫事业作出了重要贡献.
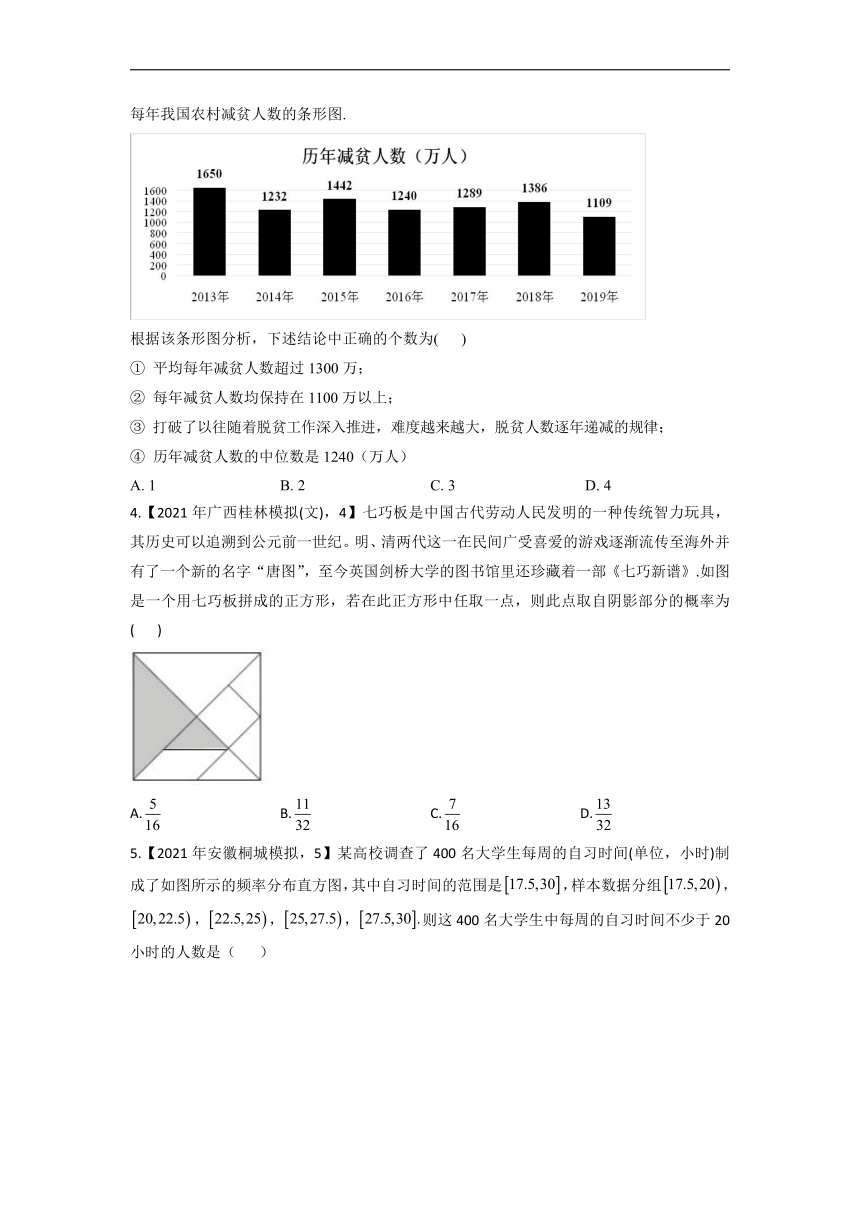
2020年为脱贫攻坚收官之年,下图为2013年至2019年每年我国农村减贫人数的条形图.
根据该条形图分析,下述结论中正确的个数为(
)
①
平均每年减贫人数超过1300万;
②
每年减贫人数均保持在1100万以上;
③
打破了以往随着脱贫工作深入推进,难度越来越大,脱贫人数逐年递减的规律;
④
历年减贫人数的中位数是1240(万人)
A.
1
B.
2
C.
3
D.
4
4.【2021年广西桂林模拟(文),4】七巧板是中国古代劳动人民发明的一种传统智力玩具,其历史可以追溯到公元前一世纪。明、清两代这一在民间广受喜爱的游戏逐渐流传至海外并有了一个新的名字“唐图”,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自阴影部分的概率为(
)
A.
B.
C.
D.
5.【2021年安徽桐城模拟,5】某高校调查了400名大学生每周的自习时间(单位,小时)制成了如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组,,,,则这400名大学生中每周的自习时间不少于20小时的人数是(
)
A.
320
B.
340
C.
360
D.
380
6.【2021年全国乙卷(文),7】在区间随机取1个数,则取到的数小于的概率为(
)
A.
B.
C.
D.
7.【2021年甘肃白银模拟(文),14】某公司有职800人,其中不到30岁的有120人,30岁到40岁的有400人,40岁以上的有280人.为了了解该公司职工与身体状况有关的某项指标,要从中抽取200名职工作为样本,职工年龄与这项指标有关,则应该选择的抽样方法是__________,40岁以上的职工应抽取________名.
8.【2021年安徽桐城模拟,14】在边长为6的正方形中有一封闭曲线围成的阴影区域,从该正方形区域内任取一点,若该点落在阴影区域内的概率为,则阴影区域的面积为_____________.
9.【2021年湖北十堰模拟,17】某公司为了解服务质量,随机调査了100位男性顾客和100位女性顾客,每位顾客对该公司的服务质量进行打分.已知这200位顾客所打分数均在之间,根据这些数据得到如下的频数分布表:
顾客所打分数
男性顾客人数
4
6
10
30
50
女性顾客人数
6
10
24
40
20
(1)求这200位顾客所打分数的平均值(同一组数据用该组区间的中点值为代表).
(2)若顾客所打分数不低于70分,则该顾客对公司服务质量的态度为满意;若顾客所打分数低于70分,则该顾客对公司服务质量的态度为不满意。根据所给数据,完成下列2×2列联表,并根据列联表,判断是否有99%的把握认为顾客对公司服务质量的态度与性别有关?
满意
不满意
男性顾客
女性顾客
附:,
0.050
0.010
0.001
k
3.841
6.635
10.828
10.【2021年广西桂林模拟(文),17】《中华人民共和国道路交通安全法》规定:机动车行驶时,驾驶人、乘坐人员应当按规定使用安全带,摩托车驾驶人及乘坐人员应当按规定佩戴安全头盔.虽然电动自行车不属于机动车,但是电动自行车使用频率高且车速较快,据统计摩托车、电动自行车驾乘人员死亡事故中约80%为颅脑损伤致死.为了维护电动自行车使用人的生命健康安全,全国多个地区出台各项规定要求电动自行车驾驶人和乘坐人都必须佩戴安全头盔.下表是某市一主干路段,交警对电动车驾驶人和乘坐人“不佩戴安全头盔”人数统计数据:
月份
6
7
8
9
10
不佩戴安全头盔人数
115
100
95
90
70
(1)请利用所给数据求出该路段电动自行车驾驶人和乘坐人“不佩戴安全头盔”人数y与月份x之间的线性回归方程.
(2)利用(1)中的回归方程,预测该路段12月份“不佩戴安全头盔”驾驶人和乘车人人数;
附:,.
11.【2021年全国乙卷(文),17】某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备
9.8
10.3
10.0
10.2
9.9
9.8
10.0
10.1
10.2
9.7
新设备
10.1
10.4
10.1
10.0
10.1
10.3
10.6
10.5
10.4
10.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和.
(1)求,,,;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
12.【2021年全国甲卷(文),17】甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如表:
一级品
二级品
合计
甲机床
150
50
200
乙机床
120
80
200
合计
270
130
400
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?
附:,
0.050
0.010
0.001
k
3.841
6.635
10.828
13.【2021年四川简阳模拟(文),18】近年来,随着国家综合国力的提升和科技的进步,截至2018年底,中国铁路运营里程达13.2万千米,这个数字比1949年增长了5倍;高铁运营里程突破2.9万千米,占世界高铁运营里程的以上,居世界第一位.如表截取了年中国高铁密度的发展情况(单位:千米/万平方千米).
年份
年份代码
1
2
3
4
5
高铁密度
已知高铁密度y与年份代码x之间满足关系式(为大于0的常数).
(1)根据所给数据,求y关于x的回归方程(精确到位);
(2)利用(1)的结论,预测到哪一年,高铁密度会超过32千米/万平方千米.
参考公式:设具有线性相关系的两个变量的一组数据为,则回归方程的系数:,
参考数据:,,,,,.
14.【2021年安徽桐城模拟,19】从2017年1月18日开始,支付宝用户可以通过“扫福字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如表:
是否集齐五福
性别
是
否
合计
男
30
10
40
女
35
5
40
合计
65
15
80
(1)根据如上的列联表,能否在犯错误的概率不超过0.05的前提下,认为“集齐五福与性别有关”?
(2)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(3)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
参考公式:.
附表:
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
15.【2021年安徽怀宁模拟,19】某新能源汽车制造公司,为鼓励消费者购买其生产的特斯拉汽车,约定从今年元月开始,凡购买一辆该品牌汽车,在行驶三年后,公司将给予适当金额的购车补贴.某调研机构对已购买该品牌汽车的消费者,就购车补贴金额的心理预期值进行了抽样调查,得其样本频率分布直方图如图所示.
(1)估计已购买该品牌汽车的消费群体对购车补贴金额的心理预期值的平均数和中位数(精确到0.01);
(2)统计今年以来元月~5月该品牌汽车的市场销售量,得其频数分布表如下:
月份
元月
2月
3月
4月
5月
销售量(万辆)
0.5
0.6
1.0
1.4
1.7
预测该品牌汽车在今年6月份的销售量约为多少万辆?
附:对于一组样本数据,,…,,其回归直线的斜率和截距的最小二乘估计值分别为,.
答案以及解析
1.答案:C
解析:本题考查频率分布直方图、均值等统计图表及统计量的基础知识.
选项
正误
原因
A
√
由图可知,组距是1,前2个小矩形的面积和是0.06
B
√
最后4个小矩形的面积和是0.10
C
×
可以求得平均值是
D
√
4.5至8.5之间小矩形的面积和是0.64
2.答案:A
解析:由频率分布直方图,得:,的频率为,,的频率为,估计这100名同学的得分的中位数为:.故选:A.
3.答案:C
解析:由图易知①
②
③正确,④中位数应为1289(万),④错,故选C
4.答案:A
解析:设正方形边长为a,则其面积,阴影部分面积,所求概率.
5.答案:D
解析:由频率分直方图得:
这400名大学生中每周的自习时间不少于20小时的频率为:,
∴这400名大学生中每周的自习时间不少于20小时的人数为:.
故选D.
6.答案:B
解析:本题考查几何概型的计算.利用几何概型的计算公式,可得.
7.答案:分层抽样;70
解析:因为职工年龄与这项指标有关,所以应该选择分层抽样,且40岁以上的职工应抽取的人数为.
8.答案:16
解析:设阴影部分的面积为S,结合几何概型公式可得:,解得:.
故答案为:16.
9.答案:(1)由题可知,这200位顾客所打分数的平均值为,
故这200位顾客所打分数的平均值为75.55.
(2)根据所给数据,可得列联表:
满意
不满意
男性顾客
80
20
女性顾客
60
40
根据列联表得.
因为,所以有99%的把握认为顾客对公司服务质量的态度与性别有关.
10.答案:(1),,
,
,
所以,y与x之间的回归直线方程为;
(2)当时,,
预测该路段12月份的“不佩戴安全头盔”驾驶人与乘车人为54人.
11.答案:(1)由题中的数据,可得,
,
,
.
(2),
,
所以,
则新设备生产产品的该项指标的均值较旧设备有显著提高.
12.答案:(1)根据题表中数据知,甲机床生产的产品中一级品的频率是,乙机床生产的产品中一级品的频率是.
(2)根据题表中的数据可得.
因为,所以有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异.
13.答案:(1)对两边取自然对数得:.
令,,,则与具有线性相关关系;
,
,
,关于的回归方程为:,,即.
(2)由(1)知:,
高铁密度超过32千米/万平方千米,即,即,
,解得:,即当时,高铁密度超过32千米/万平方千米.
预测年,高铁密度超过32千米/万平方千米.
14.答案:(1)根据列联表中的数据,得到的观测值为,
故不能在犯错误的概率不超过0.05的前提下,认为“集齐五福与性别有关”;
(2)这80位大学生集齐五福的频率为,
据此估算该校10000名在读大学生中集齐五福的人数为;
(3)设选取的2位男生和3位女生分别记为,,,,,
随机选取3次采访的所有结果为:,,,,,,,,,,
共有10个基本事件,至少有一位男生的基本事件有9个,
故所求概率为.
15.答案:(1)因为直方图的组距为1,则各组频率即为相应小矩形的高,所以平均数的估计
值为万元.
因为,则中位数在区间内.设中位数为,
则,得,所以中位数的估计值为3.33万元.
(2)记,,,,,,
由散点图可知,5组样本数据呈线性相关关系.
因为,,
,
则,,
所以回归直线方程是.
当时,,预计该品牌汽车在今年6月份的销售量约为2万辆.
1.【2021年全国甲卷(文),2】为了解某地农村经济情况,对该地农户家庭年收入进行抽样调査,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是(
)
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
2.【2021年四川简阳模拟(文),3】霍兰德职业能力测试问卷可以为大学生在择业方面提供参考,对人的能力兴趣等方面进行评估.某大学随机抽取100名学生进行霍兰德职业能力测试问卷测试,测试结果发现这100名学生的得分都在内,按得分分成5组:,,,,,得到如图所示的频率分布直方图,则这100名同学得分的中位数为(
)
A.72.5
B.75
C.77.5
D.80
3.【2021年吉林长春模拟(文),4】党的十八大以来,我们在脱贫攻坚领域取得了前所未有的成就,农村贫困人口大幅减少,解决困扰中华民族几千年的贫困问题,取得历史性成就.
同时为全球减贫事业作出了重要贡献.
2020年为脱贫攻坚收官之年,下图为2013年至2019年每年我国农村减贫人数的条形图.
根据该条形图分析,下述结论中正确的个数为(
)
①
平均每年减贫人数超过1300万;
②
每年减贫人数均保持在1100万以上;
③
打破了以往随着脱贫工作深入推进,难度越来越大,脱贫人数逐年递减的规律;
④
历年减贫人数的中位数是1240(万人)
A.
1
B.
2
C.
3
D.
4
4.【2021年广西桂林模拟(文),4】七巧板是中国古代劳动人民发明的一种传统智力玩具,其历史可以追溯到公元前一世纪。明、清两代这一在民间广受喜爱的游戏逐渐流传至海外并有了一个新的名字“唐图”,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自阴影部分的概率为(
)
A.
B.
C.
D.
5.【2021年安徽桐城模拟,5】某高校调查了400名大学生每周的自习时间(单位,小时)制成了如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组,,,,则这400名大学生中每周的自习时间不少于20小时的人数是(
)
A.
320
B.
340
C.
360
D.
380
6.【2021年全国乙卷(文),7】在区间随机取1个数,则取到的数小于的概率为(
)
A.
B.
C.
D.
7.【2021年甘肃白银模拟(文),14】某公司有职800人,其中不到30岁的有120人,30岁到40岁的有400人,40岁以上的有280人.为了了解该公司职工与身体状况有关的某项指标,要从中抽取200名职工作为样本,职工年龄与这项指标有关,则应该选择的抽样方法是__________,40岁以上的职工应抽取________名.
8.【2021年安徽桐城模拟,14】在边长为6的正方形中有一封闭曲线围成的阴影区域,从该正方形区域内任取一点,若该点落在阴影区域内的概率为,则阴影区域的面积为_____________.
9.【2021年湖北十堰模拟,17】某公司为了解服务质量,随机调査了100位男性顾客和100位女性顾客,每位顾客对该公司的服务质量进行打分.已知这200位顾客所打分数均在之间,根据这些数据得到如下的频数分布表:
顾客所打分数
男性顾客人数
4
6
10
30
50
女性顾客人数
6
10
24
40
20
(1)求这200位顾客所打分数的平均值(同一组数据用该组区间的中点值为代表).
(2)若顾客所打分数不低于70分,则该顾客对公司服务质量的态度为满意;若顾客所打分数低于70分,则该顾客对公司服务质量的态度为不满意。根据所给数据,完成下列2×2列联表,并根据列联表,判断是否有99%的把握认为顾客对公司服务质量的态度与性别有关?
满意
不满意
男性顾客
女性顾客
附:,
0.050
0.010
0.001
k
3.841
6.635
10.828
10.【2021年广西桂林模拟(文),17】《中华人民共和国道路交通安全法》规定:机动车行驶时,驾驶人、乘坐人员应当按规定使用安全带,摩托车驾驶人及乘坐人员应当按规定佩戴安全头盔.虽然电动自行车不属于机动车,但是电动自行车使用频率高且车速较快,据统计摩托车、电动自行车驾乘人员死亡事故中约80%为颅脑损伤致死.为了维护电动自行车使用人的生命健康安全,全国多个地区出台各项规定要求电动自行车驾驶人和乘坐人都必须佩戴安全头盔.下表是某市一主干路段,交警对电动车驾驶人和乘坐人“不佩戴安全头盔”人数统计数据:
月份
6
7
8
9
10
不佩戴安全头盔人数
115
100
95
90
70
(1)请利用所给数据求出该路段电动自行车驾驶人和乘坐人“不佩戴安全头盔”人数y与月份x之间的线性回归方程.
(2)利用(1)中的回归方程,预测该路段12月份“不佩戴安全头盔”驾驶人和乘车人人数;
附:,.
11.【2021年全国乙卷(文),17】某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备
9.8
10.3
10.0
10.2
9.9
9.8
10.0
10.1
10.2
9.7
新设备
10.1
10.4
10.1
10.0
10.1
10.3
10.6
10.5
10.4
10.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和.
(1)求,,,;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
12.【2021年全国甲卷(文),17】甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如表:
一级品
二级品
合计
甲机床
150
50
200
乙机床
120
80
200
合计
270
130
400
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?
附:,
0.050
0.010
0.001
k
3.841
6.635
10.828
13.【2021年四川简阳模拟(文),18】近年来,随着国家综合国力的提升和科技的进步,截至2018年底,中国铁路运营里程达13.2万千米,这个数字比1949年增长了5倍;高铁运营里程突破2.9万千米,占世界高铁运营里程的以上,居世界第一位.如表截取了年中国高铁密度的发展情况(单位:千米/万平方千米).
年份
年份代码
1
2
3
4
5
高铁密度
已知高铁密度y与年份代码x之间满足关系式(为大于0的常数).
(1)根据所给数据,求y关于x的回归方程(精确到位);
(2)利用(1)的结论,预测到哪一年,高铁密度会超过32千米/万平方千米.
参考公式:设具有线性相关系的两个变量的一组数据为,则回归方程的系数:,
参考数据:,,,,,.
14.【2021年安徽桐城模拟,19】从2017年1月18日开始,支付宝用户可以通过“扫福字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如表:
是否集齐五福
性别
是
否
合计
男
30
10
40
女
35
5
40
合计
65
15
80
(1)根据如上的列联表,能否在犯错误的概率不超过0.05的前提下,认为“集齐五福与性别有关”?
(2)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(3)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
参考公式:.
附表:
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
15.【2021年安徽怀宁模拟,19】某新能源汽车制造公司,为鼓励消费者购买其生产的特斯拉汽车,约定从今年元月开始,凡购买一辆该品牌汽车,在行驶三年后,公司将给予适当金额的购车补贴.某调研机构对已购买该品牌汽车的消费者,就购车补贴金额的心理预期值进行了抽样调查,得其样本频率分布直方图如图所示.
(1)估计已购买该品牌汽车的消费群体对购车补贴金额的心理预期值的平均数和中位数(精确到0.01);
(2)统计今年以来元月~5月该品牌汽车的市场销售量,得其频数分布表如下:
月份
元月
2月
3月
4月
5月
销售量(万辆)
0.5
0.6
1.0
1.4
1.7
预测该品牌汽车在今年6月份的销售量约为多少万辆?
附:对于一组样本数据,,…,,其回归直线的斜率和截距的最小二乘估计值分别为,.
答案以及解析
1.答案:C
解析:本题考查频率分布直方图、均值等统计图表及统计量的基础知识.
选项
正误
原因
A
√
由图可知,组距是1,前2个小矩形的面积和是0.06
B
√
最后4个小矩形的面积和是0.10
C
×
可以求得平均值是
D
√
4.5至8.5之间小矩形的面积和是0.64
2.答案:A
解析:由频率分布直方图,得:,的频率为,,的频率为,估计这100名同学的得分的中位数为:.故选:A.
3.答案:C
解析:由图易知①
②
③正确,④中位数应为1289(万),④错,故选C
4.答案:A
解析:设正方形边长为a,则其面积,阴影部分面积,所求概率.
5.答案:D
解析:由频率分直方图得:
这400名大学生中每周的自习时间不少于20小时的频率为:,
∴这400名大学生中每周的自习时间不少于20小时的人数为:.
故选D.
6.答案:B
解析:本题考查几何概型的计算.利用几何概型的计算公式,可得.
7.答案:分层抽样;70
解析:因为职工年龄与这项指标有关,所以应该选择分层抽样,且40岁以上的职工应抽取的人数为.
8.答案:16
解析:设阴影部分的面积为S,结合几何概型公式可得:,解得:.
故答案为:16.
9.答案:(1)由题可知,这200位顾客所打分数的平均值为,
故这200位顾客所打分数的平均值为75.55.
(2)根据所给数据,可得列联表:
满意
不满意
男性顾客
80
20
女性顾客
60
40
根据列联表得.
因为,所以有99%的把握认为顾客对公司服务质量的态度与性别有关.
10.答案:(1),,
,
,
所以,y与x之间的回归直线方程为;
(2)当时,,
预测该路段12月份的“不佩戴安全头盔”驾驶人与乘车人为54人.
11.答案:(1)由题中的数据,可得,
,
,
.
(2),
,
所以,
则新设备生产产品的该项指标的均值较旧设备有显著提高.
12.答案:(1)根据题表中数据知,甲机床生产的产品中一级品的频率是,乙机床生产的产品中一级品的频率是.
(2)根据题表中的数据可得.
因为,所以有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异.
13.答案:(1)对两边取自然对数得:.
令,,,则与具有线性相关关系;
,
,
,关于的回归方程为:,,即.
(2)由(1)知:,
高铁密度超过32千米/万平方千米,即,即,
,解得:,即当时,高铁密度超过32千米/万平方千米.
预测年,高铁密度超过32千米/万平方千米.
14.答案:(1)根据列联表中的数据,得到的观测值为,
故不能在犯错误的概率不超过0.05的前提下,认为“集齐五福与性别有关”;
(2)这80位大学生集齐五福的频率为,
据此估算该校10000名在读大学生中集齐五福的人数为;
(3)设选取的2位男生和3位女生分别记为,,,,,
随机选取3次采访的所有结果为:,,,,,,,,,,
共有10个基本事件,至少有一位男生的基本事件有9个,
故所求概率为.
15.答案:(1)因为直方图的组距为1,则各组频率即为相应小矩形的高,所以平均数的估计
值为万元.
因为,则中位数在区间内.设中位数为,
则,得,所以中位数的估计值为3.33万元.
(2)记,,,,,,
由散点图可知,5组样本数据呈线性相关关系.
因为,,
,
则,,
所以回归直线方程是.
当时,,预计该品牌汽车在今年6月份的销售量约为2万辆.
同课章节目录
