2021年高考数学真题模拟试题专项汇编之不等式选讲(Word版,含解析)
文档属性
| 名称 | 2021年高考数学真题模拟试题专项汇编之不等式选讲(Word版,含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 889.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 00:00:00 | ||
图片预览




文档简介
(14)不等式选讲——2021年高考数学真题模拟试题专项汇编
1.【2021年全国甲卷(理),23】已知函数,.
(1)画出和的图象;
(2)若,求a的取值范围.
2.【2021年全国乙卷(理),23】已知函数.
(1)当时,求不等式的解集;
(2)若,求a的取值范围.
3.【2021年陕西榆林模拟(文),23】已知函数.
(1)求不等式的解集;
(2)若关于x的不等式的解集是空集,求实数a的取值范围.
4.【2021年安徽桐城模拟,23】已知函数.
(1)求不等式的解集
(2)若直线与函数的图象有公共点,求k的取值范围
5.【2021年安徽怀宁模拟,23】已知函数.
(1)当时,求不等式的解集;
(2)设关于x的不等式的解集为M,且,求实数m的取值范围.
6.【2021年山西运城模拟(理),23】设函数.
(1)试比较与的大小;
(2)当时,求函数的图象和x轴围成的图形面积.
7.【2021年广西桂林模拟(文),23】已知函数,.
(1)若的最小值为2,求实数a的值;
(2)若关于x的不等式的解集为A,若,求实数a的取值范围.
8.【2021年广西北海模拟(理),23】设函数.
(1)当时,求不等式的解集;
(2)若,,求a的取值范围.
9.【2021年甘肃白银模拟(文),23】已知函数.
(1)当时,求不等式的解集;
(2)当时,若关于x的不等式恰有2个整数解,求实数m的取值范围.
10.【2021年四川简阳模拟(文),23】已知函数.
(1)若,求不等式的解集;
(2)当函数的最小值取得最小值时,求m的值.
11.【2021年江西赣县模拟(文),23】已知.
(1)求不等式的解集;
(2)若的最小值为m,正实数满足,求证:.
12.【2021年江西新余模拟(理),23】已知不等式的解集为.
(1)求m,n的值;
(2)若,,求证:.
13.【2021年安徽黄山模拟(理),23】已知函数.
(1)当时,求不等式的解集;
(2)若,不等式恒成立,求实数a的取值范围.
14.【2021年安徽安庆模拟(文),23】已知函数.
(1)当时,求不等式的解集;
(2)若,不等式恒成立,求实数a的取值范围.
答案以及解析
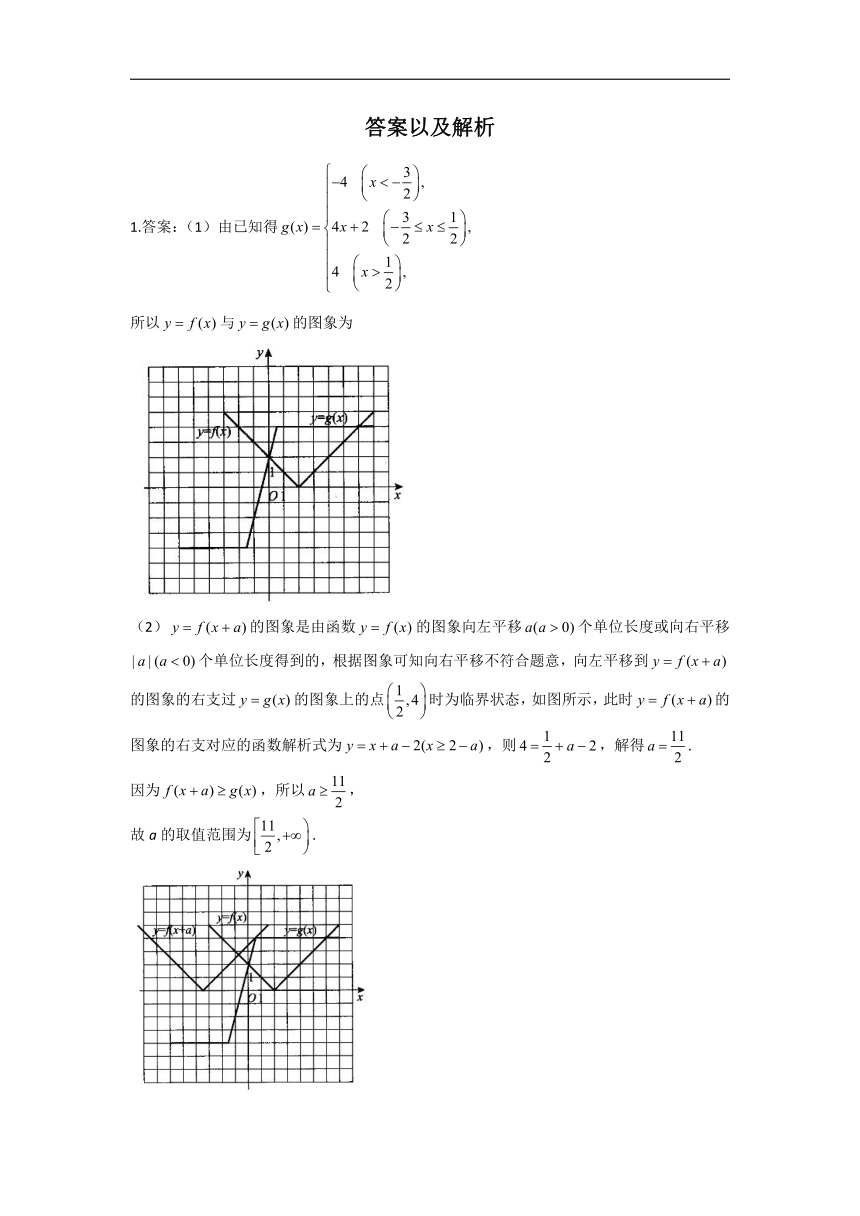
1.答案:(1)由已知得
所以与的图象为
(2)的图象是由函数的图象向左平移个单位长度或向右平移个单位长度得到的,根据图象可知向右平移不符合题意,向左平移到的图象的右支过的图象上的点时为临界状态,如图所示,此时的图象的右支对应的函数解析式为,则,解得.
因为,所以,
故a的取值范围为.
2.答案:(1)当时,
因为,所以或或
所以或,
所以不等式的解集为.
(2),
当且仅当时等号成立.
若,则,
两边平方可得,解得,
即a的取值范围是.
3.答案:(1),
,或,或.
解得或或.
不等式的解集为.
(2),
又的解集是空集,的解集是空集,
,解得.
不等式解集是空集,则实数a的取值范围为.
4.答案:(1)由,得或或,
解得,故不等式的解集为
(2)
作出函数的图象,如图所示,
直线过定点,
当此直线经过点时,
;当此直线与直线平行时,
故由图可知
5.答案:(1)因为当时,函数,
所以不等式,即,
故有①或②或③,
解①求得,解②求得,解③求得,
综上可得,不等式的解集为.
(2)由题意可得,当时,关于x的不等式恒成立,
等价于对恒成立,
即对恒成立,∴对恒成立,
等价于对恒成立,
即在上恒成立,
,即实数m的取值范围为.
6.答案:(1)因为,
于是,
当且仅当时等号成立.
(2)当时,,
可知函数的图象和x轴围成的图形是一个三角形,
其中与x轴的两个交点分别为,,三角形另一顶点坐标为,
从而的面积.
7.答案:(1),
,解得:或-6.
(2)由得:,
当时,,即:,
,即:
由,,解得:.
即a的取值范围为:.
8.答案:(1)当时,,
故不等式的解集为.
(2),
,则,解得,
故a的取值范围为.
9.答案:(1)由已知不等式,得.
当时,不等式为,解得,所以;
当时,不等式为,解得,所以;
当时,不等式为,解得,此时无解.
综上,原不等式的解集为.
(2)由题意,函数,可得,
则的单调递增区间为,单调递减区间为.
又,,,,
所以,所以,
故m的取值范围为.
10.答案:(1)当时,不等式即为.
当时,原不等式即为,解得;
当时,原不等式即为(恒成立),故;
当时,原不等式即为,解得,故.
综上所述,不等式的解集为.
(2)因为,当且仅当时,等号成立.所以.
因为,当且仅当,又,所以时,等号成立,
所以当函数的最小值取得最小值时,m的值为1.
11.答案:(1)①当时,,无解;
②当时,,解得;
③当时,,,
综上:不等式的解集为.
(2)因为,所以,
所以,
,
当且仅当,即时,等号成立.
12.答案:(1)原不等式化为或或,
解得或或,
取并集,可得原不等式的解集为,
又不等式的解集为,
∴.
(2)证明:由(1)及,可得,即,
∴,
当且仅当时取“=”.
∴.
13.答案:(1)当时,函数,
当时,由,可得,解得;
当时,由,可得,解得;
当时,由,可得,此时解集为空集,
综上所述:不等式的解集为.
(2)若,函数
由一次函数性质可知在为减函数,在为增函数,
所以,
因为不等式恒成立,即,即,解得
又因为,所以实数a的取值范围.
14.答案:(1)当时,
即
当时,即,从而有;
当时,即,从而有;
当时,即,此时为;
综上所述:
(2)若,
由函数性质可知在为减函数,在为增函数,
所以
题意为,即,从而得
又,故
1.【2021年全国甲卷(理),23】已知函数,.
(1)画出和的图象;
(2)若,求a的取值范围.
2.【2021年全国乙卷(理),23】已知函数.
(1)当时,求不等式的解集;
(2)若,求a的取值范围.
3.【2021年陕西榆林模拟(文),23】已知函数.
(1)求不等式的解集;
(2)若关于x的不等式的解集是空集,求实数a的取值范围.
4.【2021年安徽桐城模拟,23】已知函数.
(1)求不等式的解集
(2)若直线与函数的图象有公共点,求k的取值范围
5.【2021年安徽怀宁模拟,23】已知函数.
(1)当时,求不等式的解集;
(2)设关于x的不等式的解集为M,且,求实数m的取值范围.
6.【2021年山西运城模拟(理),23】设函数.
(1)试比较与的大小;
(2)当时,求函数的图象和x轴围成的图形面积.
7.【2021年广西桂林模拟(文),23】已知函数,.
(1)若的最小值为2,求实数a的值;
(2)若关于x的不等式的解集为A,若,求实数a的取值范围.
8.【2021年广西北海模拟(理),23】设函数.
(1)当时,求不等式的解集;
(2)若,,求a的取值范围.
9.【2021年甘肃白银模拟(文),23】已知函数.
(1)当时,求不等式的解集;
(2)当时,若关于x的不等式恰有2个整数解,求实数m的取值范围.
10.【2021年四川简阳模拟(文),23】已知函数.
(1)若,求不等式的解集;
(2)当函数的最小值取得最小值时,求m的值.
11.【2021年江西赣县模拟(文),23】已知.
(1)求不等式的解集;
(2)若的最小值为m,正实数满足,求证:.
12.【2021年江西新余模拟(理),23】已知不等式的解集为.
(1)求m,n的值;
(2)若,,求证:.
13.【2021年安徽黄山模拟(理),23】已知函数.
(1)当时,求不等式的解集;
(2)若,不等式恒成立,求实数a的取值范围.
14.【2021年安徽安庆模拟(文),23】已知函数.
(1)当时,求不等式的解集;
(2)若,不等式恒成立,求实数a的取值范围.
答案以及解析
1.答案:(1)由已知得
所以与的图象为
(2)的图象是由函数的图象向左平移个单位长度或向右平移个单位长度得到的,根据图象可知向右平移不符合题意,向左平移到的图象的右支过的图象上的点时为临界状态,如图所示,此时的图象的右支对应的函数解析式为,则,解得.
因为,所以,
故a的取值范围为.
2.答案:(1)当时,
因为,所以或或
所以或,
所以不等式的解集为.
(2),
当且仅当时等号成立.
若,则,
两边平方可得,解得,
即a的取值范围是.
3.答案:(1),
,或,或.
解得或或.
不等式的解集为.
(2),
又的解集是空集,的解集是空集,
,解得.
不等式解集是空集,则实数a的取值范围为.
4.答案:(1)由,得或或,
解得,故不等式的解集为
(2)
作出函数的图象,如图所示,
直线过定点,
当此直线经过点时,
;当此直线与直线平行时,
故由图可知
5.答案:(1)因为当时,函数,
所以不等式,即,
故有①或②或③,
解①求得,解②求得,解③求得,
综上可得,不等式的解集为.
(2)由题意可得,当时,关于x的不等式恒成立,
等价于对恒成立,
即对恒成立,∴对恒成立,
等价于对恒成立,
即在上恒成立,
,即实数m的取值范围为.
6.答案:(1)因为,
于是,
当且仅当时等号成立.
(2)当时,,
可知函数的图象和x轴围成的图形是一个三角形,
其中与x轴的两个交点分别为,,三角形另一顶点坐标为,
从而的面积.
7.答案:(1),
,解得:或-6.
(2)由得:,
当时,,即:,
,即:
由,,解得:.
即a的取值范围为:.
8.答案:(1)当时,,
故不等式的解集为.
(2),
,则,解得,
故a的取值范围为.
9.答案:(1)由已知不等式,得.
当时,不等式为,解得,所以;
当时,不等式为,解得,所以;
当时,不等式为,解得,此时无解.
综上,原不等式的解集为.
(2)由题意,函数,可得,
则的单调递增区间为,单调递减区间为.
又,,,,
所以,所以,
故m的取值范围为.
10.答案:(1)当时,不等式即为.
当时,原不等式即为,解得;
当时,原不等式即为(恒成立),故;
当时,原不等式即为,解得,故.
综上所述,不等式的解集为.
(2)因为,当且仅当时,等号成立.所以.
因为,当且仅当,又,所以时,等号成立,
所以当函数的最小值取得最小值时,m的值为1.
11.答案:(1)①当时,,无解;
②当时,,解得;
③当时,,,
综上:不等式的解集为.
(2)因为,所以,
所以,
,
当且仅当,即时,等号成立.
12.答案:(1)原不等式化为或或,
解得或或,
取并集,可得原不等式的解集为,
又不等式的解集为,
∴.
(2)证明:由(1)及,可得,即,
∴,
当且仅当时取“=”.
∴.
13.答案:(1)当时,函数,
当时,由,可得,解得;
当时,由,可得,解得;
当时,由,可得,此时解集为空集,
综上所述:不等式的解集为.
(2)若,函数
由一次函数性质可知在为减函数,在为增函数,
所以,
因为不等式恒成立,即,即,解得
又因为,所以实数a的取值范围.
14.答案:(1)当时,
即
当时,即,从而有;
当时,即,从而有;
当时,即,此时为;
综上所述:
(2)若,
由函数性质可知在为减函数,在为增函数,
所以
题意为,即,从而得
又,故
同课章节目录
