第二章 统计单元测试B卷-2021-2022学年高二数学人教A版必修3(Word含解析)
文档属性
| 名称 | 第二章 统计单元测试B卷-2021-2022学年高二数学人教A版必修3(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 365.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 20:33:08 | ||
图片预览


文档简介
2021-2022学年高二数学人教A版必修3第二章
统计单元测试B卷
一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在抽查产品尺寸的过程中,将其尺寸分成若干组,是其中的一组,抽查出的个体尺寸在该组内的频率为m,该组上的直方图高为h,则(
)
A.hm
B.
C.
D.
2.为了解工厂的1000名工人的生产情况,从中抽取100名工人进行统计,得到如下频率分布直方图,由此可估计该工厂产量在75件及以上的工人数为(
)
A.50
B.100
C.150
D.250
3.某班全体学生英语测试成绩(单位:分)的频率分布直方图如图所示,数据的分组依次为,,,.若低于60分的人数是15,则该班的学生人数是(
)
A.45
B.50
C.55
D.60
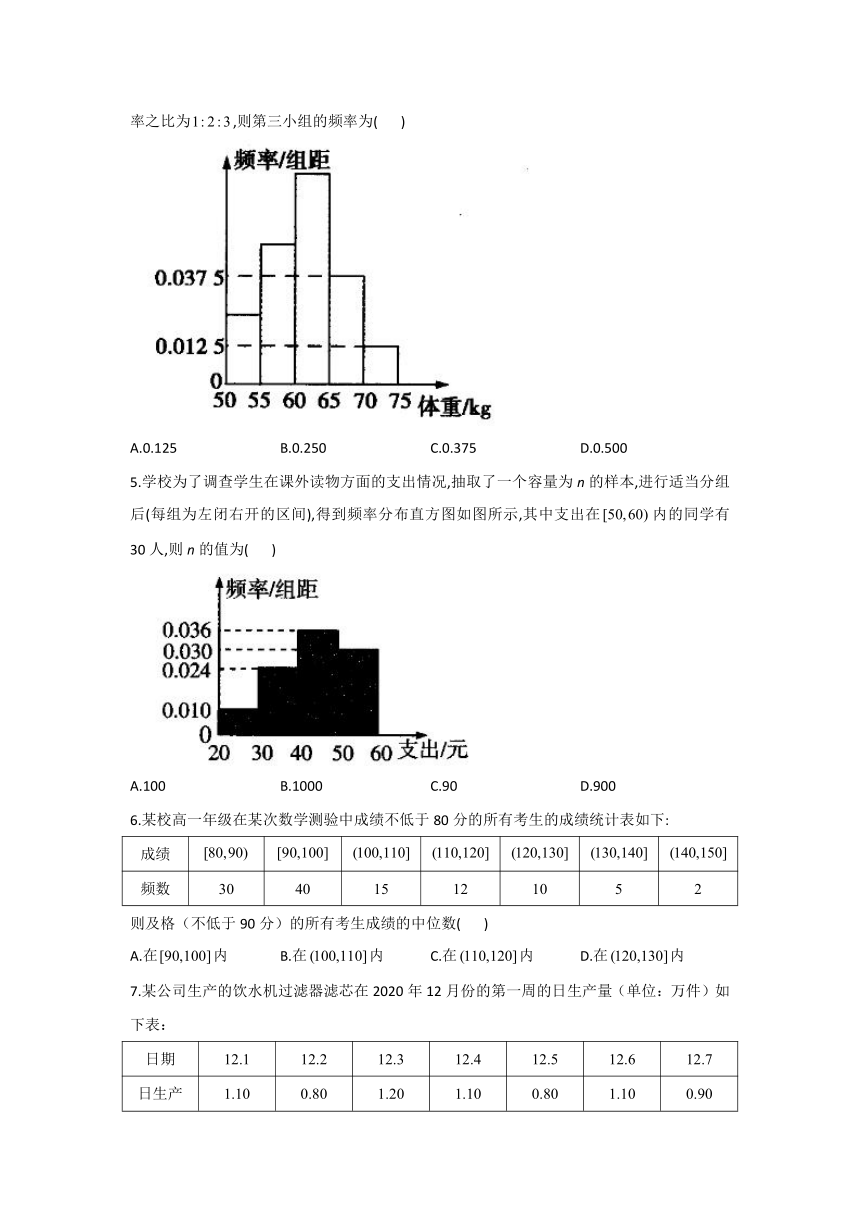
4.如图是某中学高一学生体重(单位:kg)的频率分布直方图,已知图中从左到右的前三组的频率之比为,则第三小组的频率为(
)
A.0.125
B.0.250
C.0.375
D.0.500
5.学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,进行适当分组后(每组为左闭右开的区间),得到频率分布直方图如图所示,其中支出在内的同学有30人,则n的值为(
)
A.100
B.1000
C.90
D.900
6.某校高一年级在某次数学测验中成绩不低于80分的所有考生的成绩统计表如下:
成绩
频数
30
40
15
12
10
5
2
则及格(不低于90分)的所有考生成绩的中位数(
)
A.在内
B.在内
C.在内
D.在内
7.某公司生产的饮水机过滤器滤芯在2020年12月份的第一周的日生产量(单位:万件)如下表:
日期
12.1
12.2
12.3
12.4
12.5
12.6
12.7
日生产量/万件
1.10
0.80
1.20
1.10
0.80
1.10
0.90
则该公司这一周的日生产量的方差为(精确到0.01)(
)
A.0.02
B.0.01
C.0.03
D.0.04
8.某中学有高中生3500人,初中生1500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为的样本,已知从高中生中抽取70人,则为(?
?)
A.100????????
B.150????????
C.200????????
D.250
9.某中学高中部共有80名教师,初中部共有120名教师,其性别比例如图所示,现从中按分层抽样抽取25人进行优质课展示,则应抽取高中部男教师的人数为(
)
A.3
B.6
C.7
D.9
10.为落实《国家学生体质健康标准》达标测试工作,全面提升学生的体质健康水平,某校高二年级体育组教师在高二年级随机抽取100名男生,测试了立定跳远项目,依据测试数据绘制了如图所示的频率直方图.已知立定跳远195
cm及以上成绩为合格,255
cm以上成绩为优秀,根据图中的数据估计全校1000名男生中立定跳远项目合格的男生有(
)
A.660名
B.940名
C.970名
D.800名
二、填空题:本题共5小题,每小题5分,共25分.
11.数据8、10、12、9、11的极差和方差分别是____________________.
12.从编号为1,2,…,88的88个网站中采用系统抽样的方法抽取容量为8的样本,若所抽样本中有编号为53的网站,则样本中网站的最小编号为__________.
13.如图所示的茎叶图记录了甲、乙两组各3名同学在期末考试中的数学成绩,则方差较小的那组同学成绩的方差为__________。
14.2020年8月8日是我国第12个全民健身日,中小学生每天的运动时长备受社会关注.某市教育部门从该市中小学生中随机抽查了2000名,调查他们
7月份的日平均运动时长(单位:小时),得到的频率分布直方图如图所示,若日平均运动时长在区间内的人数仅为区间内人数的一半,则样本中中小学生日平均运动时长在内的人数为___________.
15.某中学高一、高二、高三学生的人数比为.为了了解学生的课外阅读情况,计划从全校学生中采用按年级分层随机抽样的方法抽取总数的的学生进行调查若样本中高一学生比高二学生少6人,则全校学生的总人数为_________.
三、解答题:本题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.
16.
(10分)某互联网公司为了确定下季度的前期广告投入计划,收集了近6个月广告投入量x(单位:万元)和收益y(单位:万元)的数据如表:
月份
1
2
3
4
5
6
广告投入量
2
4
6
8
10
12
收益
14.21
20.31
31.8
31.18
37.83
44.67
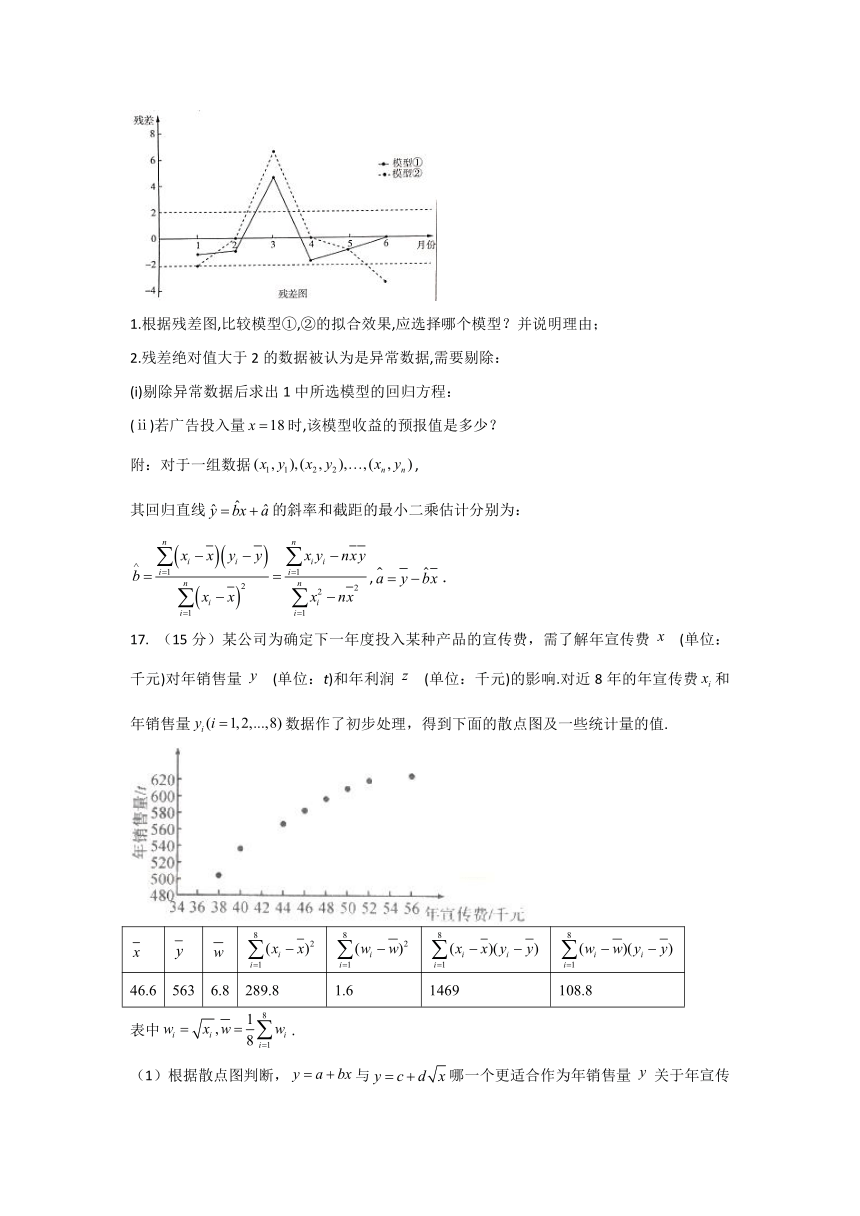
他们分别用两种模型①,②分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值;
7
30
1464.24
364
1.根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
2.残差绝对值大于2的数据被认为是异常数据,需要剔除:
(i)剔除异常数据后求出1中所选模型的回归方程:
(ⅱ)若广告投入量时,该模型收益的预报值是多少?
附:对于一组数据,
其回归直线的斜率和截距的最小二乘估计分别为:
,.
17.
(15分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
(单位:千元)对年销售量
(单位:t)和年利润
(单位:千元)的影响.对近8年的年宣传费和年销售量数据作了初步处理,得到下面的散点图及一些统计量的值.
46.6
563
6.8
289.8
1.6
1469
108.8
表中.
(1)根据散点图判断,与哪一个更适合作为年销售量关于年宣传费的回归方程类型(给出判断即可,不必说明理由),并根据判断结果及表中数据,建立关于的回归方程;
(2)已知这种产品的年利润与的关系为.
(i)年宣传费时,年利润的预报值是多少?
(ii)年宣传费为何值时,年利润的预报值最大?
附:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为
答案以及解析
1.答案:B
解析:根据频率分布直方图中每组的高为频率/组距,可知,所以,故选B.
2.答案:C
解析:产量在75件以上(含75件)的频率为,所以该工厂产量在75件以上(含75件)的工人数为.故选C.
3.答案:B
解析:根据频率分布直方图,可知低于60分的人数的频率是,所以该班的学生人数是.
4.答案:C
解析:由频率分布直方图,知前三组的频率之和为,所以第三小组的频率为,故选C.
5.答案:A
解析:由频率分布直方图可知,支出在内的同学的频率为,所以,故选A.
6.答案:B
解析:由表可知,及格的考生共有人,在内有40人,在内有15人,故及格的所有考生成绩的中位数在内.
7.答案:A
解析:设这一周的日生产量为x,
则,
所以方差.
8.答案:A
解析:计算分层抽样的抽取比例和总体个数,利用样本容量=总体个数×抽取比例计算值.
分层抽样的抽取比例为,
总体个数为,
∴样本容量.
故选:A.
9.答案:B
解析:高中部的男教师人数为,所以应抽取高中部男教师的人数为.
10.答案:B
解析:由图可知,所以实数,所以可估计全校1000名男生中立定跳远项目合格的男生有名.
11.答案:4、2
解析:极差为最大值减去最小值,
,
,
,
所以极差和方差分别是4和2.
12.答案:9
解析:抽样间隔为,则样本中比53小的网站编号有42,31,20,9,故样本中网站的最小编号为9.
13.答案:
解析:,
,
,
,
所以方差较小的那组同学成绩的方差为?。
14.答案:1650
解析:日平均运动时长在区间和内的频率之和为.由题意可知,日平均运动时长在区间内的频率为内的一半,所以日平均运动时长在区间内的频率为0.1,在内的频率为0.2,因此日平均运动时长在内的频率为,故样本中中小学生日平均运动时长在内的人数为.
15.答案:780
解析:多法解题:方法一:设样本中高一、高二、高三学生的人数依次为,则由题意得,解得.所以样本中高一、高二、高三学生的人数依次为21,27,30.因为是从全校学生中采用分层随机抽样的方法抽取总数的的学生进行调查,所以高一、高二、高三学生的人数依次为210,270,,300.所以全校学生的总人数为
方法二:因为采用按年级分层随机抽样的方法抽取总数的的学生,且样本中高一学生比高二学生少6人,所以高学生比高二学生少60人.因为高一、高二、高三学生的人数比为,所以全校学生的总人数为.
16.答案:1.由于模型①残差波动小,应该选择模型①
2.(i)剔除异常数据,即组号为3的数据
剩下数据的平均数为,
∴,
∴所选模型的回归方程为
(ⅱ)若广告投入量时,该模型收益的预报值是.
17.答案:(1)根据散点图可判断,更合适作为关于的回归方程类型.
令,先建立关于的线性回归方程,由表中数据得:
所以关于的回归方程为
所以关于的回归方程为
(2)(ⅰ)当时,年销售量的预报值,年利润的预报值
(ⅱ)年利润的预报值
年利润,即时,取得最大值.
统计单元测试B卷
一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在抽查产品尺寸的过程中,将其尺寸分成若干组,是其中的一组,抽查出的个体尺寸在该组内的频率为m,该组上的直方图高为h,则(
)
A.hm
B.
C.
D.
2.为了解工厂的1000名工人的生产情况,从中抽取100名工人进行统计,得到如下频率分布直方图,由此可估计该工厂产量在75件及以上的工人数为(
)
A.50
B.100
C.150
D.250
3.某班全体学生英语测试成绩(单位:分)的频率分布直方图如图所示,数据的分组依次为,,,.若低于60分的人数是15,则该班的学生人数是(
)
A.45
B.50
C.55
D.60
4.如图是某中学高一学生体重(单位:kg)的频率分布直方图,已知图中从左到右的前三组的频率之比为,则第三小组的频率为(
)
A.0.125
B.0.250
C.0.375
D.0.500
5.学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,进行适当分组后(每组为左闭右开的区间),得到频率分布直方图如图所示,其中支出在内的同学有30人,则n的值为(
)
A.100
B.1000
C.90
D.900
6.某校高一年级在某次数学测验中成绩不低于80分的所有考生的成绩统计表如下:
成绩
频数
30
40
15
12
10
5
2
则及格(不低于90分)的所有考生成绩的中位数(
)
A.在内
B.在内
C.在内
D.在内
7.某公司生产的饮水机过滤器滤芯在2020年12月份的第一周的日生产量(单位:万件)如下表:
日期
12.1
12.2
12.3
12.4
12.5
12.6
12.7
日生产量/万件
1.10
0.80
1.20
1.10
0.80
1.10
0.90
则该公司这一周的日生产量的方差为(精确到0.01)(
)
A.0.02
B.0.01
C.0.03
D.0.04
8.某中学有高中生3500人,初中生1500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为的样本,已知从高中生中抽取70人,则为(?
?)
A.100????????
B.150????????
C.200????????
D.250
9.某中学高中部共有80名教师,初中部共有120名教师,其性别比例如图所示,现从中按分层抽样抽取25人进行优质课展示,则应抽取高中部男教师的人数为(
)
A.3
B.6
C.7
D.9
10.为落实《国家学生体质健康标准》达标测试工作,全面提升学生的体质健康水平,某校高二年级体育组教师在高二年级随机抽取100名男生,测试了立定跳远项目,依据测试数据绘制了如图所示的频率直方图.已知立定跳远195
cm及以上成绩为合格,255
cm以上成绩为优秀,根据图中的数据估计全校1000名男生中立定跳远项目合格的男生有(
)
A.660名
B.940名
C.970名
D.800名
二、填空题:本题共5小题,每小题5分,共25分.
11.数据8、10、12、9、11的极差和方差分别是____________________.
12.从编号为1,2,…,88的88个网站中采用系统抽样的方法抽取容量为8的样本,若所抽样本中有编号为53的网站,则样本中网站的最小编号为__________.
13.如图所示的茎叶图记录了甲、乙两组各3名同学在期末考试中的数学成绩,则方差较小的那组同学成绩的方差为__________。
14.2020年8月8日是我国第12个全民健身日,中小学生每天的运动时长备受社会关注.某市教育部门从该市中小学生中随机抽查了2000名,调查他们
7月份的日平均运动时长(单位:小时),得到的频率分布直方图如图所示,若日平均运动时长在区间内的人数仅为区间内人数的一半,则样本中中小学生日平均运动时长在内的人数为___________.
15.某中学高一、高二、高三学生的人数比为.为了了解学生的课外阅读情况,计划从全校学生中采用按年级分层随机抽样的方法抽取总数的的学生进行调查若样本中高一学生比高二学生少6人,则全校学生的总人数为_________.
三、解答题:本题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.
16.
(10分)某互联网公司为了确定下季度的前期广告投入计划,收集了近6个月广告投入量x(单位:万元)和收益y(单位:万元)的数据如表:
月份
1
2
3
4
5
6
广告投入量
2
4
6
8
10
12
收益
14.21
20.31
31.8
31.18
37.83
44.67
他们分别用两种模型①,②分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值;
7
30
1464.24
364
1.根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
2.残差绝对值大于2的数据被认为是异常数据,需要剔除:
(i)剔除异常数据后求出1中所选模型的回归方程:
(ⅱ)若广告投入量时,该模型收益的预报值是多少?
附:对于一组数据,
其回归直线的斜率和截距的最小二乘估计分别为:
,.
17.
(15分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
(单位:千元)对年销售量
(单位:t)和年利润
(单位:千元)的影响.对近8年的年宣传费和年销售量数据作了初步处理,得到下面的散点图及一些统计量的值.
46.6
563
6.8
289.8
1.6
1469
108.8
表中.
(1)根据散点图判断,与哪一个更适合作为年销售量关于年宣传费的回归方程类型(给出判断即可,不必说明理由),并根据判断结果及表中数据,建立关于的回归方程;
(2)已知这种产品的年利润与的关系为.
(i)年宣传费时,年利润的预报值是多少?
(ii)年宣传费为何值时,年利润的预报值最大?
附:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为
答案以及解析
1.答案:B
解析:根据频率分布直方图中每组的高为频率/组距,可知,所以,故选B.
2.答案:C
解析:产量在75件以上(含75件)的频率为,所以该工厂产量在75件以上(含75件)的工人数为.故选C.
3.答案:B
解析:根据频率分布直方图,可知低于60分的人数的频率是,所以该班的学生人数是.
4.答案:C
解析:由频率分布直方图,知前三组的频率之和为,所以第三小组的频率为,故选C.
5.答案:A
解析:由频率分布直方图可知,支出在内的同学的频率为,所以,故选A.
6.答案:B
解析:由表可知,及格的考生共有人,在内有40人,在内有15人,故及格的所有考生成绩的中位数在内.
7.答案:A
解析:设这一周的日生产量为x,
则,
所以方差.
8.答案:A
解析:计算分层抽样的抽取比例和总体个数,利用样本容量=总体个数×抽取比例计算值.
分层抽样的抽取比例为,
总体个数为,
∴样本容量.
故选:A.
9.答案:B
解析:高中部的男教师人数为,所以应抽取高中部男教师的人数为.
10.答案:B
解析:由图可知,所以实数,所以可估计全校1000名男生中立定跳远项目合格的男生有名.
11.答案:4、2
解析:极差为最大值减去最小值,
,
,
,
所以极差和方差分别是4和2.
12.答案:9
解析:抽样间隔为,则样本中比53小的网站编号有42,31,20,9,故样本中网站的最小编号为9.
13.答案:
解析:,
,
,
,
所以方差较小的那组同学成绩的方差为?。
14.答案:1650
解析:日平均运动时长在区间和内的频率之和为.由题意可知,日平均运动时长在区间内的频率为内的一半,所以日平均运动时长在区间内的频率为0.1,在内的频率为0.2,因此日平均运动时长在内的频率为,故样本中中小学生日平均运动时长在内的人数为.
15.答案:780
解析:多法解题:方法一:设样本中高一、高二、高三学生的人数依次为,则由题意得,解得.所以样本中高一、高二、高三学生的人数依次为21,27,30.因为是从全校学生中采用分层随机抽样的方法抽取总数的的学生进行调查,所以高一、高二、高三学生的人数依次为210,270,,300.所以全校学生的总人数为
方法二:因为采用按年级分层随机抽样的方法抽取总数的的学生,且样本中高一学生比高二学生少6人,所以高学生比高二学生少60人.因为高一、高二、高三学生的人数比为,所以全校学生的总人数为.
16.答案:1.由于模型①残差波动小,应该选择模型①
2.(i)剔除异常数据,即组号为3的数据
剩下数据的平均数为,
∴,
∴所选模型的回归方程为
(ⅱ)若广告投入量时,该模型收益的预报值是.
17.答案:(1)根据散点图可判断,更合适作为关于的回归方程类型.
令,先建立关于的线性回归方程,由表中数据得:
所以关于的回归方程为
所以关于的回归方程为
(2)(ⅰ)当时,年销售量的预报值,年利润的预报值
(ⅱ)年利润的预报值
年利润,即时,取得最大值.
