2021-2022学年沪科版 九年级数学上册22.2相似三角形判定第四课时直角三角形相似判定课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年沪科版 九年级数学上册22.2相似三角形判定第四课时直角三角形相似判定课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 07:34:15 | ||
图片预览


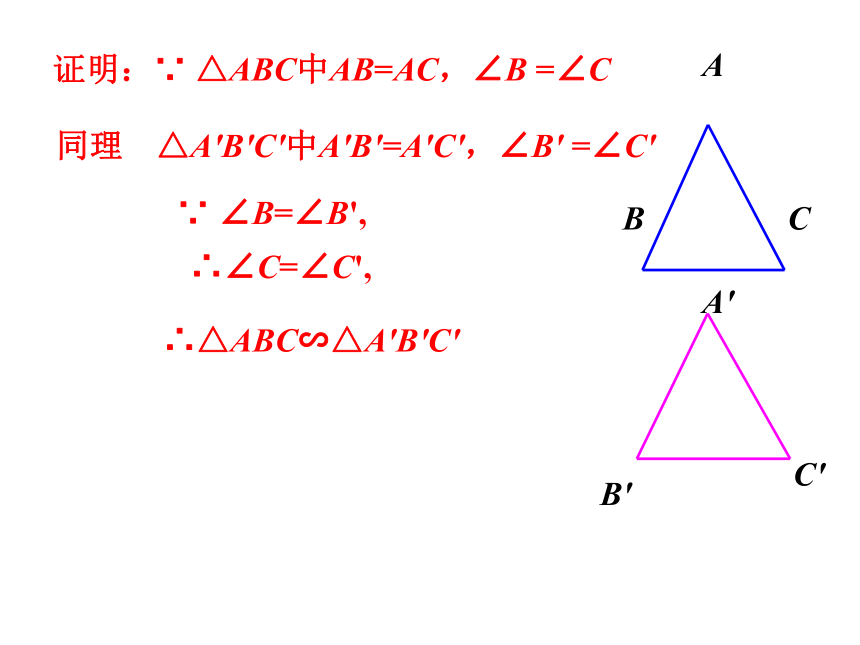
文档简介
(共19张PPT)
22.2
相似三角形的判定
第四课时
直角四角形相似的判定
沪科版数学九年级上
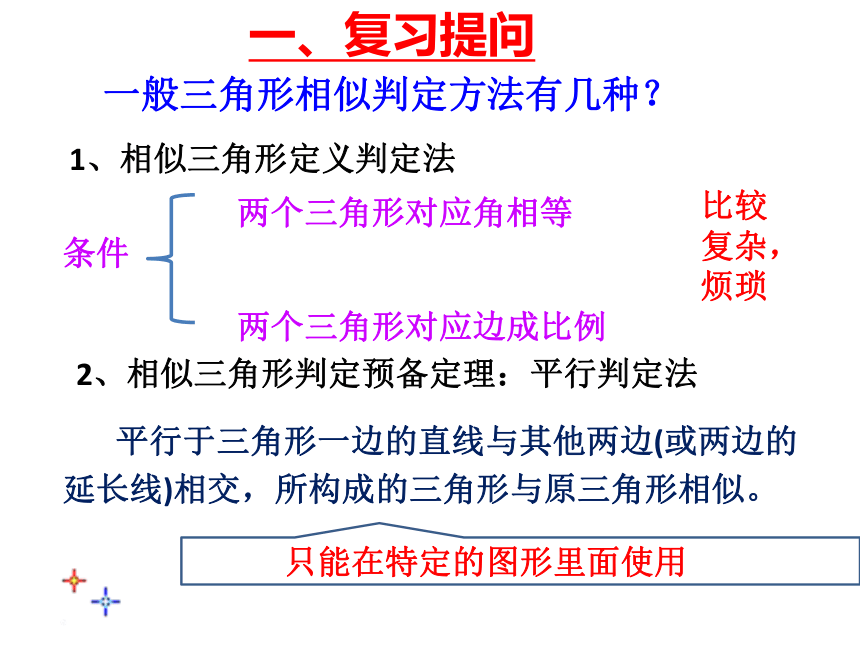
一般三角形相似判定方法有几种?
1、相似三角形定义判定法
2、相似三角形判定预备定理:平行判定法
比较复杂,烦琐
一、复习提问
条件
两个三角形对应边成比例
两个三角形对应角相等
平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
只能在特定的图形里面使用
3、角角判定法(AA)
4、边角边判定法(SAS)
5、边边边判定法(SSS)
(1)两角对应相等的两个三角形相似。
(2)两边对应成比例且夹角相等的两个三角形相似
(3)三边对应成比例的两个三角形相似。
思考:
我们学过哪些特殊的三角形?
等腰三角形
等边三角形
直角三角形
它们的相似判定有什么不同吗?
讨论:
两个等腰三角形一定相似吗?
两个等边三角形一定相似吗?
两个直角三角形一定相似吗?
两个等腰直角三角形一定相似吗?
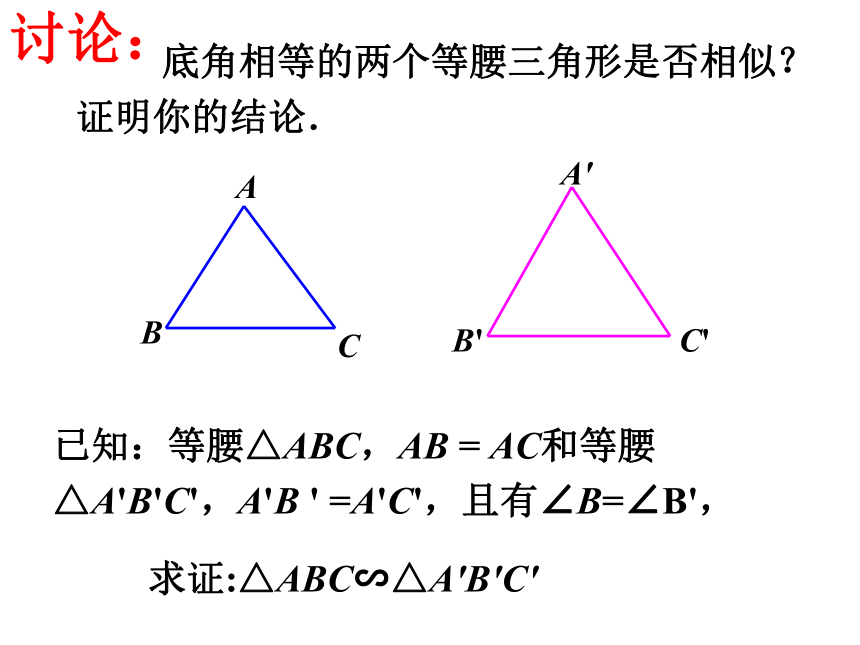
底角相等的两个等腰三角形是否相似?证明你的结论.
B
A
C
B'
A'
C'
已知:等腰△ABC,AB
=
AC和等腰△A'B'C',A'B
'
=A'C',且有∠B=∠B',
求证:△ABC∽△A'B'C'
讨论:
证明:∵
△ABC中AB=AC,∠B
=∠C
B
A
C
B'
A'
C'
同理
△A'B'C'中A'B'=A'C',∠B'
=∠C'
∵
∠B=∠B',
∴∠C=∠C',
∴△ABC∽△A'B'C'
B
A
C
B'
A'
C'
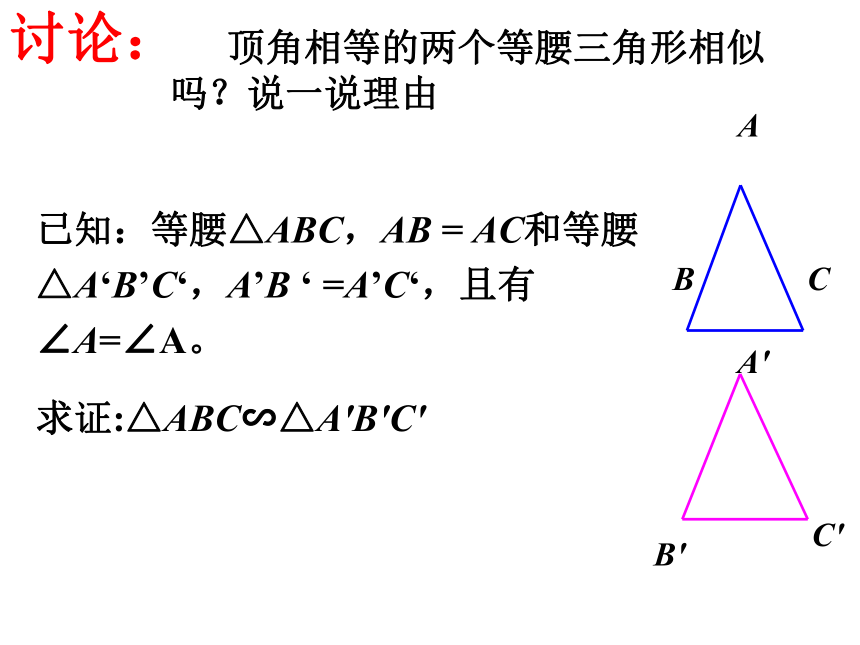
顶角相等的两个等腰三角形相似吗?说一说理由
讨论:
已知:等腰△ABC,AB
=
AC和等腰△A‘B’C‘,A’B
‘
=A’C‘,且有∠A=∠A。
求证:△ABC∽△A'B'C'
证明:∵
△ABC中AB=AC,∠B
=∠C
∴
2∠B
=180°-∠A
同理
△A'B'C'中A'B'=A'C',∠B'
=∠C'
∴
2∠B'
=180°-∠A'
又
∠A=∠A'
∴
∠B=∠B',
∴
△ABC∽△A'B'C'
B
A
C
B'
A'
C'
如图,Rt△ABC中,CD是斜边上的高,△ACD和△CBD都和△ABC相似吗?
A
B
C
D
1
2
△ACD∽△ABC
△CBD∽△ABC
讨论:
有一个锐角相等的两直角三角形相似
命题:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
在Rt△ABC中,∠C=90°,AB=10,AC=8;
在Rt△DEF中,∠D=90°,EF=5,
DE=4,
这两个直角三角形相似吗?
讨论:
已知:如图所示,Rt△ABC与Rt△A′B′C′中,
∠C=∠C′=90°,
求证:Rt△ABC∽Rt△A′B′C′
∴
=k
A
B
C
A′
B′
C′
证明:∵设
=k,则
AB=kA'B',
AC=kA'C'.
∵BC2=
AB2
-AC2
=(kA'B')2
-(kA'C')2
∴BC
=
kB'C'
∴△ABC∽△A′B′C′
直角三角形相似的判定定理
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
结论:
一直角边和斜边对应成比例的两个直角三角形相似。
应用定理:
在Rt△ABC与Rt△A′B′C′中,
∠C=∠C′=90°,具有下列条件时两个直角三角形是否相似?
应用定理:
1、∠A=35°
,∠B′=________。
2、AC=5,BC=4,A′C′=15,B′C′=___。
3、AB=5,AC=___,A′B′=10,
A′C′=6。
4、AB=10,BC=6,
A′B′=5,
A′C′=______.
5、AC:AB=1:3,
A′C′=a,
A′B′=_____
55°
12
3
4
3a
应用定理:
在Rt△ABC和Rt△A′B′C′中,已知
∠C=∠C′=90°。要使Rt△ABC∽
Rt△A′B′C′,应加什么条件?
例1、如图,
在RtΔABC中,CD是斜边AB上的高。
(1)证明CD2=AD·BD
(2)类似的,AC2=(
)·(
);
BC2=(
)·(
)
∴
△CDB∽△ADC
证明:
∵∠ACB=∠ADC=90°
∴
CD2=AD·DB
∴
AC2=AD·AB,
∴
BC2=BD·BA
(2)、
∵
△ACD∽△ABC
∵
△ABC∽△CBD
B
D
A
C
1
2
CD
AD
=
BD
CD
∴
(1)
、
∴∠1+∠2=90°
∴∠A+∠2=90°
∴∠A=∠1
常用的成比例的线段:
常用的相等的角:
∠A
=∠DCB
;∠B
=∠ACD
射影定理
B
D
A
C
1
2
拓展结论:直角三角形被斜边上的高分成的两个直角三角形与原三角形都相似。
即、△ACD∽△ABC∽△CBD
“双垂直”三角形
三、小结
1、如何判定两个直角三角形相似呢?
答:一个锐角对应相等或两边对应成比例的两个直角三角形相似。
2、直角三角形相似的判定定理的简单应用。
3、初步了解转移比例的证法。
已知在△ABC中,∠C=90o
,AC=8cm,BC=6cm,点P从点A出发,沿AC以3厘米/秒的速度向点C移动,点Q从点B出发,沿BA以4厘米/秒的速度向点A移动。
如果P、Q分别从A、B
同时出发,移动时间为t秒
(0当t为何值时,以Q、A、P为顶点的三角形与△
ABC相似?
A
C
B
P
Q
Q
A
C
B
P
A
C
B
P
Q
拓展练习
22.2
相似三角形的判定
第四课时
直角四角形相似的判定
沪科版数学九年级上
一般三角形相似判定方法有几种?
1、相似三角形定义判定法
2、相似三角形判定预备定理:平行判定法
比较复杂,烦琐
一、复习提问
条件
两个三角形对应边成比例
两个三角形对应角相等
平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
只能在特定的图形里面使用
3、角角判定法(AA)
4、边角边判定法(SAS)
5、边边边判定法(SSS)
(1)两角对应相等的两个三角形相似。
(2)两边对应成比例且夹角相等的两个三角形相似
(3)三边对应成比例的两个三角形相似。
思考:
我们学过哪些特殊的三角形?
等腰三角形
等边三角形
直角三角形
它们的相似判定有什么不同吗?
讨论:
两个等腰三角形一定相似吗?
两个等边三角形一定相似吗?
两个直角三角形一定相似吗?
两个等腰直角三角形一定相似吗?
底角相等的两个等腰三角形是否相似?证明你的结论.
B
A
C
B'
A'
C'
已知:等腰△ABC,AB
=
AC和等腰△A'B'C',A'B
'
=A'C',且有∠B=∠B',
求证:△ABC∽△A'B'C'
讨论:
证明:∵
△ABC中AB=AC,∠B
=∠C
B
A
C
B'
A'
C'
同理
△A'B'C'中A'B'=A'C',∠B'
=∠C'
∵
∠B=∠B',
∴∠C=∠C',
∴△ABC∽△A'B'C'
B
A
C
B'
A'
C'
顶角相等的两个等腰三角形相似吗?说一说理由
讨论:
已知:等腰△ABC,AB
=
AC和等腰△A‘B’C‘,A’B
‘
=A’C‘,且有∠A=∠A。
求证:△ABC∽△A'B'C'
证明:∵
△ABC中AB=AC,∠B
=∠C
∴
2∠B
=180°-∠A
同理
△A'B'C'中A'B'=A'C',∠B'
=∠C'
∴
2∠B'
=180°-∠A'
又
∠A=∠A'
∴
∠B=∠B',
∴
△ABC∽△A'B'C'
B
A
C
B'
A'
C'
如图,Rt△ABC中,CD是斜边上的高,△ACD和△CBD都和△ABC相似吗?
A
B
C
D
1
2
△ACD∽△ABC
△CBD∽△ABC
讨论:
有一个锐角相等的两直角三角形相似
命题:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
在Rt△ABC中,∠C=90°,AB=10,AC=8;
在Rt△DEF中,∠D=90°,EF=5,
DE=4,
这两个直角三角形相似吗?
讨论:
已知:如图所示,Rt△ABC与Rt△A′B′C′中,
∠C=∠C′=90°,
求证:Rt△ABC∽Rt△A′B′C′
∴
=k
A
B
C
A′
B′
C′
证明:∵设
=k,则
AB=kA'B',
AC=kA'C'.
∵BC2=
AB2
-AC2
=(kA'B')2
-(kA'C')2
∴BC
=
kB'C'
∴△ABC∽△A′B′C′
直角三角形相似的判定定理
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
结论:
一直角边和斜边对应成比例的两个直角三角形相似。
应用定理:
在Rt△ABC与Rt△A′B′C′中,
∠C=∠C′=90°,具有下列条件时两个直角三角形是否相似?
应用定理:
1、∠A=35°
,∠B′=________。
2、AC=5,BC=4,A′C′=15,B′C′=___。
3、AB=5,AC=___,A′B′=10,
A′C′=6。
4、AB=10,BC=6,
A′B′=5,
A′C′=______.
5、AC:AB=1:3,
A′C′=a,
A′B′=_____
55°
12
3
4
3a
应用定理:
在Rt△ABC和Rt△A′B′C′中,已知
∠C=∠C′=90°。要使Rt△ABC∽
Rt△A′B′C′,应加什么条件?
例1、如图,
在RtΔABC中,CD是斜边AB上的高。
(1)证明CD2=AD·BD
(2)类似的,AC2=(
)·(
);
BC2=(
)·(
)
∴
△CDB∽△ADC
证明:
∵∠ACB=∠ADC=90°
∴
CD2=AD·DB
∴
AC2=AD·AB,
∴
BC2=BD·BA
(2)、
∵
△ACD∽△ABC
∵
△ABC∽△CBD
B
D
A
C
1
2
CD
AD
=
BD
CD
∴
(1)
、
∴∠1+∠2=90°
∴∠A+∠2=90°
∴∠A=∠1
常用的成比例的线段:
常用的相等的角:
∠A
=∠DCB
;∠B
=∠ACD
射影定理
B
D
A
C
1
2
拓展结论:直角三角形被斜边上的高分成的两个直角三角形与原三角形都相似。
即、△ACD∽△ABC∽△CBD
“双垂直”三角形
三、小结
1、如何判定两个直角三角形相似呢?
答:一个锐角对应相等或两边对应成比例的两个直角三角形相似。
2、直角三角形相似的判定定理的简单应用。
3、初步了解转移比例的证法。
已知在△ABC中,∠C=90o
,AC=8cm,BC=6cm,点P从点A出发,沿AC以3厘米/秒的速度向点C移动,点Q从点B出发,沿BA以4厘米/秒的速度向点A移动。
如果P、Q分别从A、B
同时出发,移动时间为t秒
(0
ABC相似?
A
C
B
P
Q
Q
A
C
B
P
A
C
B
P
Q
拓展练习
