第七章三角形 综合练习一
文档属性
| 名称 | 第七章三角形 综合练习一 |  | |
| 格式 | zip | ||
| 文件大小 | 250.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-06 17:05:05 | ||
图片预览





文档简介
(共21张PPT)
第七章 综合练习一
1.下列三条线段可以组成三角形的是( )
A、2,3.5,6 B、8,10,15 C、4,5,9 D、5,15,9
2.三角形的三个内角之比是2:3:7,这个三角形是( )
A、锐角三角形 B、直角三角形
C、等腰三角形 D、钝角三角形
3.下列各项可能是多边形的内角和是( )
A、 B、 C、 D、
B
D
C
4.等腰三角形的两边是5和9,则它的周长是_____________.
5.正多边形的一个内角比它的一个外角大100°,则这个多边形是_____边形.
6.正八边形的对角线有_______条, n边形
(n>3)的对角线有_________条.
19或23
9
20
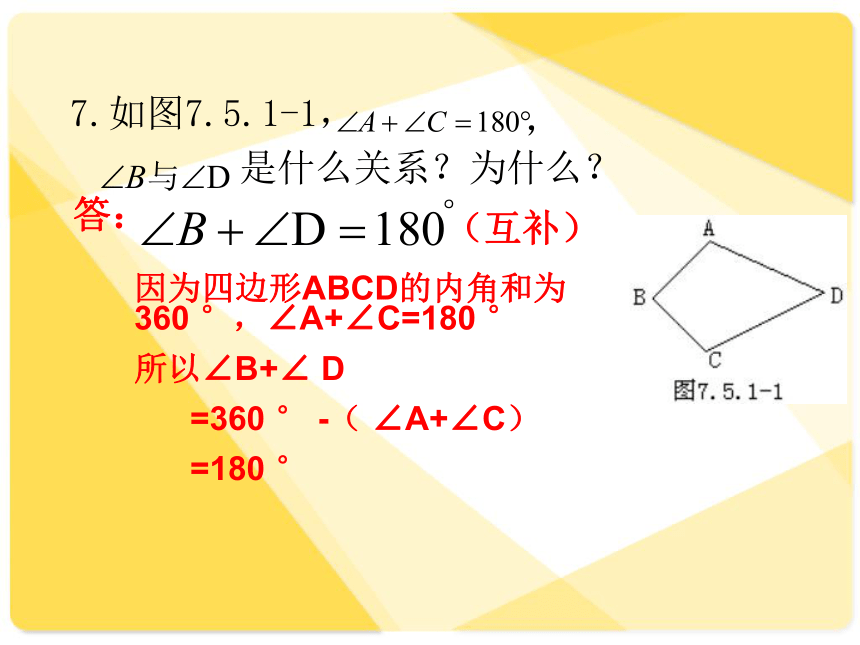
7.如图7.5.1-1,
,
是什么关系?为什么?
答:
(互补)
°
因为四边形ABCD的内角和为360 °,∠A+∠C=180 °
所以∠B+∠ D
=360 ° -( ∠A+∠C)
=180 °
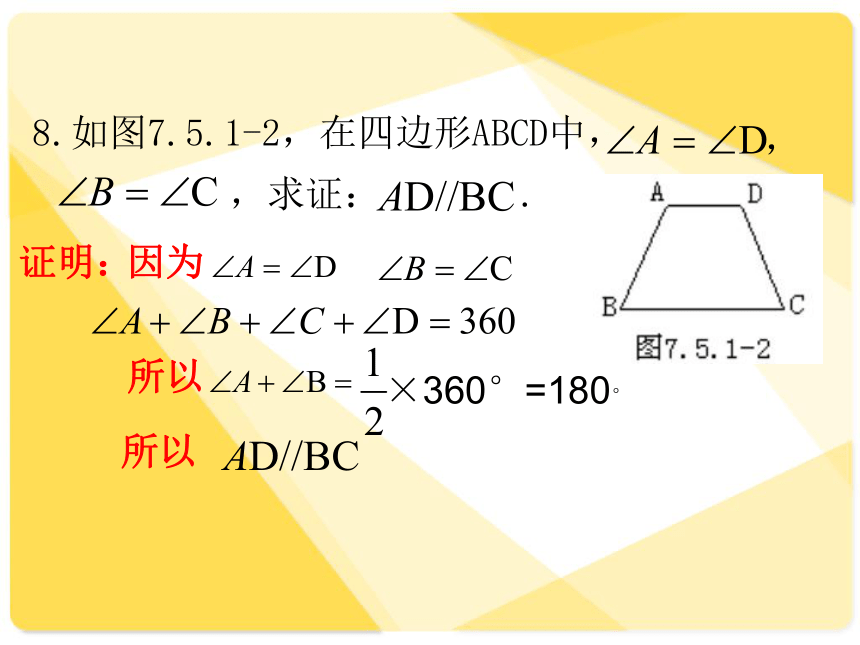
8.如图7.5.1-2,在四边形ABCD中,
,
,求证:
.
证明:
因为
所以
×360°=180°
所以
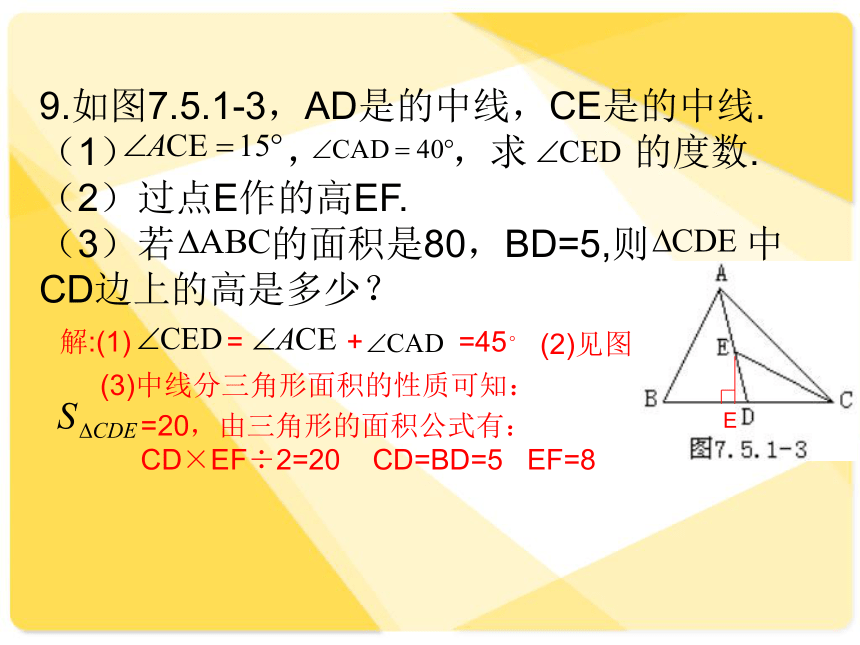
9.如图7.5.1-3,AD是的中线,CE是的中线.
(1) , ,求 的度数.
(2)过点E作的高EF.
(3)若 的面积是80,BD=5,则 中CD边上的高是多少?
解:(1) = + =45°
E
(2)见图
(3)中线分三角形面积的性质可知:
=20,由三角形的面积公式有: CD×EF÷2=20 CD=BD=5 EF=8
第七章 综合练习二
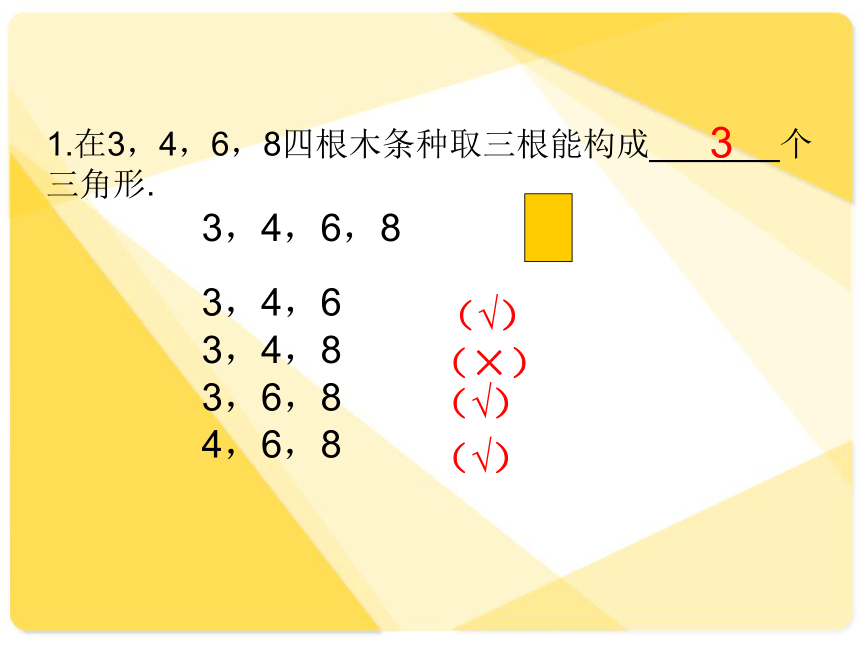
1.在3,4,6,8四根木条种取三根能构成_______个三角形.
3,4,6,8
3,4,6
3,4,8
3,6,8
4,6,8
(√)
(×)
(√)
(√)
3
2.在三角形中,至少有____个锐角,在三角形中最大的角不小于______度.
3.在 中,若∠A=2∠B:∠C=∠B+ 20° ,则这个三角形是______三角形.
2
60
锐角
分析:由三角形的内角和∠A+ ∠B+ ∠C=180°,所以:
(2∠B)+ ∠B+ (∠B+ 20 °)=180 ° 4∠B=160 °
∠B=40 ° ∠A=80 ° ∠C=60 °
4.已知等腰三角形的两边是4和7,它的周长是___________.
15或18
解:①若底为4,腰为7,可以构成三角形.
三角形的周长为:4+7+7=18
②若底为7,腰为4,可以构成三角形.
三角形的周长为:4+4+7=15
①
4
7
7
②
4
7
4
分情况讨论:
5.一个多边形的内角和是1080°,这个多边形是_____边形.
解:由多边形的内角和公式180°(n-2)得:
180°(n-2)=1080 °
n-2=6
n=8
8
变形思考:一个多边形的每个内角都是144°,它是几边形?
6.一个多边形的每个内角都是144°,它是几边形?
解:由每个内角是144°,可得:
每个外角是180°—144°=36 °
外角和为360 ° ,可知,外角的个数为:
360 °÷36 °=10
所以:它是十边形.
7.如图7.5.2-1,用相同的长方形地砖拼一个矩形,每个小长方形地砖的面积是________.
分析:此题的突破口在小长方形的长加宽的和是40cm,长是宽的3倍.(想想为什么?)
解:设宽为x,则长为3x,由题可知:
x+3x=40
x=10
小长方形的面积是30×10=300cm2
300cm2
8.如图7.5.2-2,
,
,
,则∠A=______.
E
解:延长CD,与AB相交于点E.
在三角形ACE中,由内角和定理可得:
35°
方法一:
方法二:
8.如图7.5.2-2,
,
,
,则∠A=______.
35°
解:连接AD.因为
8.如图7.5.2-2,
,
,则∠A=______.
35°
方法三:
解:连接BC.
9.如图7.5.2-3,在
中,AB=AC,若
,则
.
解:因为∠A=36 °
所以∠B+∠ACB=144 °
因为AB=AC,
所以∠B= ∠ACB=72°
72
10.如图7.5.2-4,一块直角三角形纸片,沿DE
剪去直角,那么
.
整体的思想
∠A+ ∠B =180°- ∠C
∠1+ ∠2=360°- (∠A+ ∠B )
=360°-(180°- ∠C )
=180°+ ∠C
=270°
11.如图7.5.2-5,求
的度数.
解:连接BE. 由三角形内角和可知:
∠1+ ∠2= ∠C+ ∠D
1
2
12.若以多边形的每一个顶点为圆心,半径为1画圆,如图所示.
(1)若多边形是三角形,阴影部分的面积是________。
(2)若多边形是四边形,阴影部分的面积是________。
(3)若多边形是五边形,阴影部分的面积是________。
(4)若多边形是n边形,阴影部分的面积是___________。
第七章 综合练习一
1.下列三条线段可以组成三角形的是( )
A、2,3.5,6 B、8,10,15 C、4,5,9 D、5,15,9
2.三角形的三个内角之比是2:3:7,这个三角形是( )
A、锐角三角形 B、直角三角形
C、等腰三角形 D、钝角三角形
3.下列各项可能是多边形的内角和是( )
A、 B、 C、 D、
B
D
C
4.等腰三角形的两边是5和9,则它的周长是_____________.
5.正多边形的一个内角比它的一个外角大100°,则这个多边形是_____边形.
6.正八边形的对角线有_______条, n边形
(n>3)的对角线有_________条.
19或23
9
20
7.如图7.5.1-1,
,
是什么关系?为什么?
答:
(互补)
°
因为四边形ABCD的内角和为360 °,∠A+∠C=180 °
所以∠B+∠ D
=360 ° -( ∠A+∠C)
=180 °
8.如图7.5.1-2,在四边形ABCD中,
,
,求证:
.
证明:
因为
所以
×360°=180°
所以
9.如图7.5.1-3,AD是的中线,CE是的中线.
(1) , ,求 的度数.
(2)过点E作的高EF.
(3)若 的面积是80,BD=5,则 中CD边上的高是多少?
解:(1) = + =45°
E
(2)见图
(3)中线分三角形面积的性质可知:
=20,由三角形的面积公式有: CD×EF÷2=20 CD=BD=5 EF=8
第七章 综合练习二
1.在3,4,6,8四根木条种取三根能构成_______个三角形.
3,4,6,8
3,4,6
3,4,8
3,6,8
4,6,8
(√)
(×)
(√)
(√)
3
2.在三角形中,至少有____个锐角,在三角形中最大的角不小于______度.
3.在 中,若∠A=2∠B:∠C=∠B+ 20° ,则这个三角形是______三角形.
2
60
锐角
分析:由三角形的内角和∠A+ ∠B+ ∠C=180°,所以:
(2∠B)+ ∠B+ (∠B+ 20 °)=180 ° 4∠B=160 °
∠B=40 ° ∠A=80 ° ∠C=60 °
4.已知等腰三角形的两边是4和7,它的周长是___________.
15或18
解:①若底为4,腰为7,可以构成三角形.
三角形的周长为:4+7+7=18
②若底为7,腰为4,可以构成三角形.
三角形的周长为:4+4+7=15
①
4
7
7
②
4
7
4
分情况讨论:
5.一个多边形的内角和是1080°,这个多边形是_____边形.
解:由多边形的内角和公式180°(n-2)得:
180°(n-2)=1080 °
n-2=6
n=8
8
变形思考:一个多边形的每个内角都是144°,它是几边形?
6.一个多边形的每个内角都是144°,它是几边形?
解:由每个内角是144°,可得:
每个外角是180°—144°=36 °
外角和为360 ° ,可知,外角的个数为:
360 °÷36 °=10
所以:它是十边形.
7.如图7.5.2-1,用相同的长方形地砖拼一个矩形,每个小长方形地砖的面积是________.
分析:此题的突破口在小长方形的长加宽的和是40cm,长是宽的3倍.(想想为什么?)
解:设宽为x,则长为3x,由题可知:
x+3x=40
x=10
小长方形的面积是30×10=300cm2
300cm2
8.如图7.5.2-2,
,
,
,则∠A=______.
E
解:延长CD,与AB相交于点E.
在三角形ACE中,由内角和定理可得:
35°
方法一:
方法二:
8.如图7.5.2-2,
,
,
,则∠A=______.
35°
解:连接AD.因为
8.如图7.5.2-2,
,
,则∠A=______.
35°
方法三:
解:连接BC.
9.如图7.5.2-3,在
中,AB=AC,若
,则
.
解:因为∠A=36 °
所以∠B+∠ACB=144 °
因为AB=AC,
所以∠B= ∠ACB=72°
72
10.如图7.5.2-4,一块直角三角形纸片,沿DE
剪去直角,那么
.
整体的思想
∠A+ ∠B =180°- ∠C
∠1+ ∠2=360°- (∠A+ ∠B )
=360°-(180°- ∠C )
=180°+ ∠C
=270°
11.如图7.5.2-5,求
的度数.
解:连接BE. 由三角形内角和可知:
∠1+ ∠2= ∠C+ ∠D
1
2
12.若以多边形的每一个顶点为圆心,半径为1画圆,如图所示.
(1)若多边形是三角形,阴影部分的面积是________。
(2)若多边形是四边形,阴影部分的面积是________。
(3)若多边形是五边形,阴影部分的面积是________。
(4)若多边形是n边形,阴影部分的面积是___________。
