1.2 反比例函数的图像与性质 教学案
文档属性
| 名称 | 1.2 反比例函数的图像与性质 教学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 133.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 00:00:00 | ||
图片预览

文档简介
课题 反比例函数y=(k>0)的图象与性质
教学目标
1.了解反比例函数y=(k>0)的图象为双曲线,能用描点法画其图象;
2.理解并掌握反比例函数y=(k>0)的性质;
3.体会数形结合的思想方法,培养自主探究知识的能力.
教学重点
理解并掌握反比例函数y=(k>0)的性质.
教学难点
运用反比例函数性质解决问题.
投影片、作图工具等.
导学流程
一、情景导入 感受新知
我们已经学习了用“描点法”画一次函数的图象,并且知道一次函数的图象是一条直线,那么怎样画反比例函数y=(k为常数,k≠0)的图象呢?它的图象的形状是怎样的呢?
二、自学互研 生成新知
【自主探究】
阅读教材P5~P7的内容,完成下面的问题:
1.画反比例函数y=的图象时先要__列表__,列表时自变量x可取哪些值?
__(提示:x是不为零的任何实数,所以可以以零为基准,左右均匀、对称地取值)__
2.取值以后再__描点__.
3.描点之后再__连线__:怎样连线?__可在各个象限内按照自变量从小到大的顺序用两条光滑的曲线把所描的点连接起来.__
师生合作探究并归纳出y=的图象特征.
归纳:反比例函数y=(k>0)的图象是两支分别分布在一、三象限的光滑曲线.
【合作探究】
尝试:画反比例函数y=的图象.
步骤:
1.列表:
x
-5
-4
-2
-1
-
-
1
2
4
5
y=
-0.4
-0.5
-1
-2
-4
-6
6
4
2
1
0.5
0.4
2.描点:
3.连线:在两象限内分别用圆滑曲线顺次连接.
归纳:(1)反比例函数图象的画法:(描点法)
①列表:自变量的取值应以0为中心,沿0的两边取三对(或以上)互为相反数的点,并计算出相应y值,填表;
②描点:先描出一侧,另一侧可依中心对称点性质去找.
③连线:用光滑曲线连接各点并延伸.
(2)反比例函数y=(k≠0)的图象与性质如下表:
k的符号
图象
性质
k>0
1.由于x≠0,k≠0,所以y≠0;2.当k>0时,函数图象的两个分支在一、三象限,在每个象限内,y随x的增大而减小.
k<0
1.由于x≠0,k≠0,所以y≠0;2.当k<0时,函数图象的两个分支在二、四象限,在每个象限内,y随x的增大而增大.
【师生活动】
①明了学情:关注学生对反比例函数y=(k>0)的图像和性质的掌握;
②差异指导:对学生在探究中遇到的困惑及时引导与点拨;
③生生互助:学生小组内交流讨论,相互释疑,达成共识.
三、典例剖析 运用新知
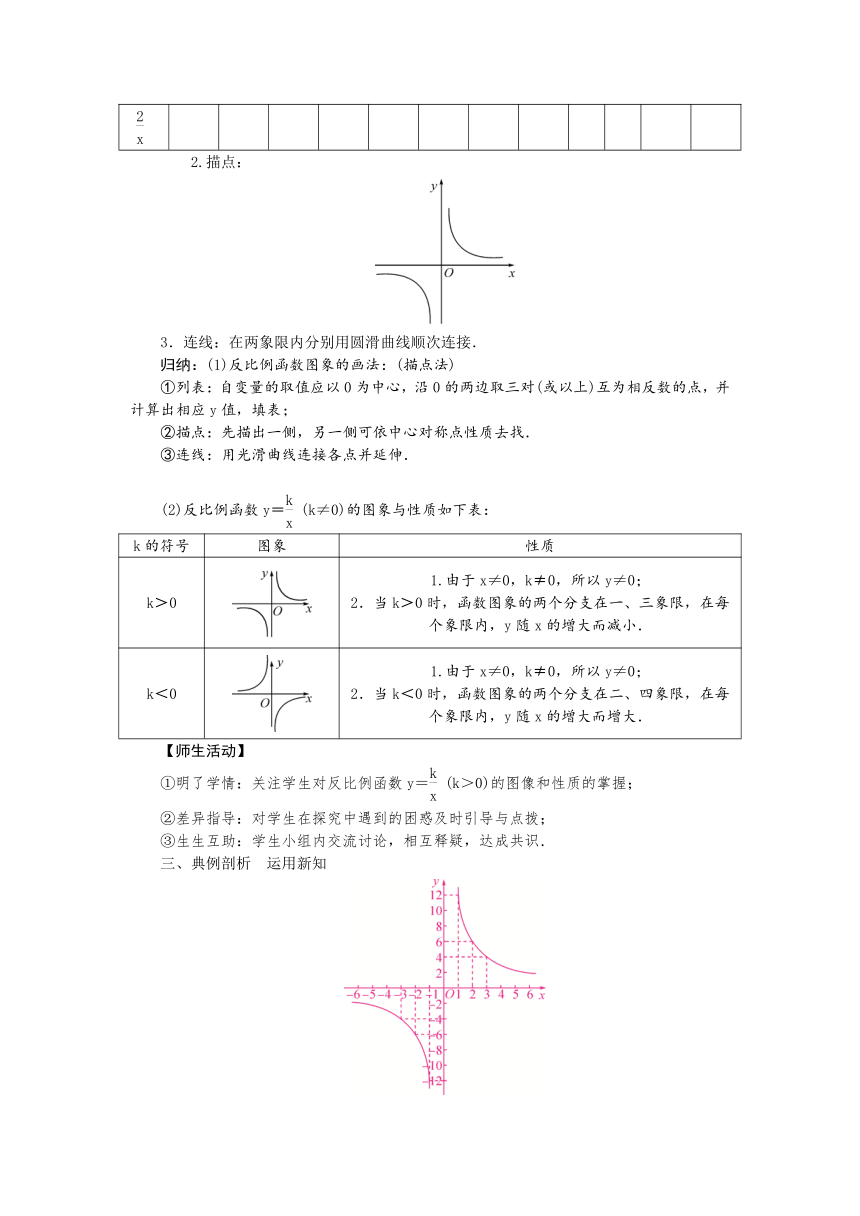
例1:作出反比例函数y=的图象,并根据图象解答下列问题:
(1)当x=4时,求y的值;(2)当y=-2时,求x的值;(3)当y>2时,求x的范围.
解:列表:
x
…
-3
-2
-1
1
2
3
…
y
…
-4
-6
-12
12
6
4
…
由图知:(1)y=3;(2)x=-6;(3)0例2:已知反比例函数y=的图象如图所示,求m的取值范围.
解:∵由图象可知,反比例函数y=的图象位于第一、三象限,∴2m+1>0,解得m>-.
四、课堂小结 回顾新知
通过本节课的学习,你有什么收获?还有哪些疑惑?请谈一谈你的想法和同学们一起分享!
【教师强调】
1.掌握反比例函数图象的画法;
2.牢记反比例函数的性质.
五、检测反馈 落实新知
1.下列反比例函数图象一定在第一、三象限的是(C)
A.y= B.y=
C.y=
D.y=
2.下列各点中,在反比例函数y=的图象上的是(C)
A.(-1,4)
B.(1,-4)
C.(1,4)
D.(2,3)
3.如图是反比例函数y=的图象的一支,根据图象回答下列问题:
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′),如果a>a′,那么b和b′有怎样的大小关系?
解:(1)另一支在第三象限.
由题意可知,m-5>0,
解得m>5.
(2)由图象可知,在每个象限内,函数值随自变量的增大而减小,∴当a>a′>0时,b0>a′时,b>b′.
六、课后作业 巩固新知
见学生用书.
教学目标
1.了解反比例函数y=(k>0)的图象为双曲线,能用描点法画其图象;
2.理解并掌握反比例函数y=(k>0)的性质;
3.体会数形结合的思想方法,培养自主探究知识的能力.
教学重点
理解并掌握反比例函数y=(k>0)的性质.
教学难点
运用反比例函数性质解决问题.
投影片、作图工具等.
导学流程
一、情景导入 感受新知
我们已经学习了用“描点法”画一次函数的图象,并且知道一次函数的图象是一条直线,那么怎样画反比例函数y=(k为常数,k≠0)的图象呢?它的图象的形状是怎样的呢?
二、自学互研 生成新知
【自主探究】
阅读教材P5~P7的内容,完成下面的问题:
1.画反比例函数y=的图象时先要__列表__,列表时自变量x可取哪些值?
__(提示:x是不为零的任何实数,所以可以以零为基准,左右均匀、对称地取值)__
2.取值以后再__描点__.
3.描点之后再__连线__:怎样连线?__可在各个象限内按照自变量从小到大的顺序用两条光滑的曲线把所描的点连接起来.__
师生合作探究并归纳出y=的图象特征.
归纳:反比例函数y=(k>0)的图象是两支分别分布在一、三象限的光滑曲线.
【合作探究】
尝试:画反比例函数y=的图象.
步骤:
1.列表:
x
-5
-4
-2
-1
-
-
1
2
4
5
y=
-0.4
-0.5
-1
-2
-4
-6
6
4
2
1
0.5
0.4
2.描点:
3.连线:在两象限内分别用圆滑曲线顺次连接.
归纳:(1)反比例函数图象的画法:(描点法)
①列表:自变量的取值应以0为中心,沿0的两边取三对(或以上)互为相反数的点,并计算出相应y值,填表;
②描点:先描出一侧,另一侧可依中心对称点性质去找.
③连线:用光滑曲线连接各点并延伸.
(2)反比例函数y=(k≠0)的图象与性质如下表:
k的符号
图象
性质
k>0
1.由于x≠0,k≠0,所以y≠0;2.当k>0时,函数图象的两个分支在一、三象限,在每个象限内,y随x的增大而减小.
k<0
1.由于x≠0,k≠0,所以y≠0;2.当k<0时,函数图象的两个分支在二、四象限,在每个象限内,y随x的增大而增大.
【师生活动】
①明了学情:关注学生对反比例函数y=(k>0)的图像和性质的掌握;
②差异指导:对学生在探究中遇到的困惑及时引导与点拨;
③生生互助:学生小组内交流讨论,相互释疑,达成共识.
三、典例剖析 运用新知
例1:作出反比例函数y=的图象,并根据图象解答下列问题:
(1)当x=4时,求y的值;(2)当y=-2时,求x的值;(3)当y>2时,求x的范围.
解:列表:
x
…
-3
-2
-1
1
2
3
…
y
…
-4
-6
-12
12
6
4
…
由图知:(1)y=3;(2)x=-6;(3)0
解:∵由图象可知,反比例函数y=的图象位于第一、三象限,∴2m+1>0,解得m>-.
四、课堂小结 回顾新知
通过本节课的学习,你有什么收获?还有哪些疑惑?请谈一谈你的想法和同学们一起分享!
【教师强调】
1.掌握反比例函数图象的画法;
2.牢记反比例函数的性质.
五、检测反馈 落实新知
1.下列反比例函数图象一定在第一、三象限的是(C)
A.y= B.y=
C.y=
D.y=
2.下列各点中,在反比例函数y=的图象上的是(C)
A.(-1,4)
B.(1,-4)
C.(1,4)
D.(2,3)
3.如图是反比例函数y=的图象的一支,根据图象回答下列问题:
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′),如果a>a′,那么b和b′有怎样的大小关系?
解:(1)另一支在第三象限.
由题意可知,m-5>0,
解得m>5.
(2)由图象可知,在每个象限内,函数值随自变量的增大而减小,∴当a>a′>0时,b
六、课后作业 巩固新知
见学生用书.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
