八年级鲁教版(五四制)数学3.4数据的离散程度(1)课件 (共20张PPT)
文档属性
| 名称 | 八年级鲁教版(五四制)数学3.4数据的离散程度(1)课件 (共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 486.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 08:12:40 | ||
图片预览







文档简介
(共20张PPT)
3.4数据的离散程度(1)
第三章
数据的分析
1.了解刻画数据离散程度的三个量度——极差、方差和标准差的概念.
2.能借助计算器求极差、方差和标准差的数值,并在具体问题中加以应用.
3.经历表示数据离散程度的几个量的探索,体会用样本估计总体的思想.
练习一
1、某校八年级五个班的学生人数分别为:
54,56,49,51,50人.
求这五个班级的平均人数.
2、数据-1,0,1,
3
,
2,2,2,1的众数是
;中位数是
.
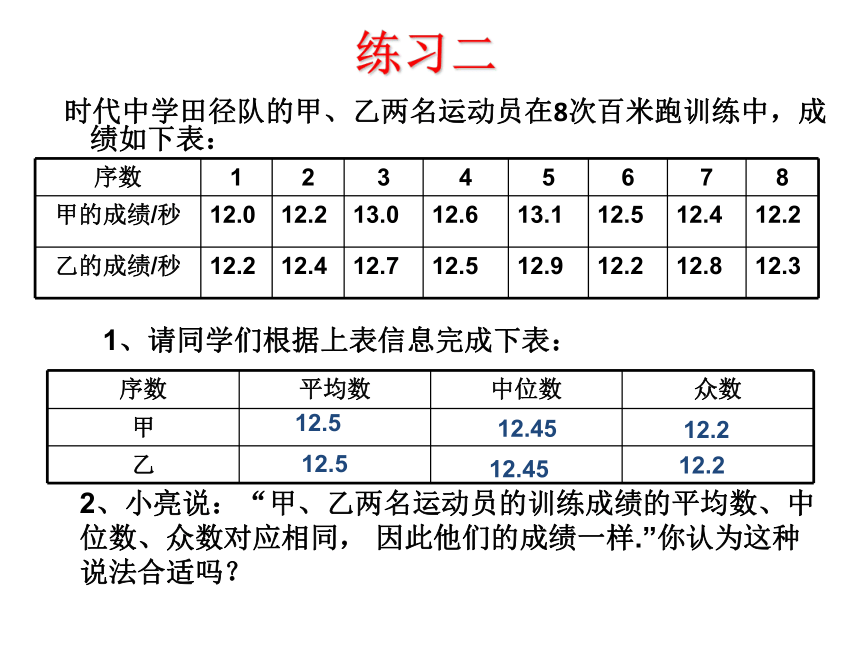
练习二
时代中学田径队的甲、乙两名运动员在8次百米跑训练中,成绩如下表:
序数
1
2
3
4
5
6
7
8
甲的成绩/秒
12.0
12.2
13.0
12.6
13.1
12.5
12.4
12.2
乙的成绩/秒
12.2
12.4
12.7
12.5
12.9
12.2
12.8
12.3
序数
平均数
中位数
众数
甲
乙
1、请同学们根据上表信息完成下表:
12.5
12.45
12.2
12.5
2、小亮说:“甲、乙两名运动员的训练成绩的平均数、中
位数、众数对应相同,
因此他们的成绩一样.”你认为这种
说法合适吗?
12.45
12.2
我国加入“WTO”后,为了提高农副产品的国际竞争力,一些行业协会对农副产品的规格进行了划分.
某外贸公司要出口一批规格为75
g的鸡腿,现有2个厂家提供货源,它们的价格相同,鸡腿品质相近.
质检员分别从甲、乙两厂的产品中抽样调查了20只鸡腿,质量(单位:g)如下:
甲厂:75
74
74
76
73
76
75
77
77
74
74
75
75
76
73
76
73
78
77
72
乙厂:75
78
72
77
74
75
73
79
72
75
80
71
76
77
73
78
71
76
73
75
问题1:如果只考虑鸡腿的规格,你认为外贸公司应该购买哪个厂的鸡腿?
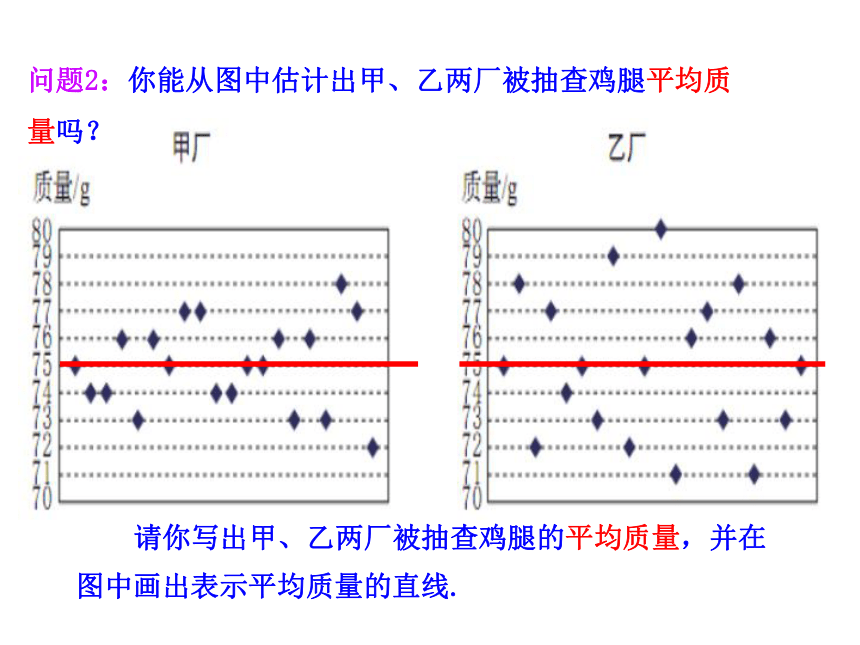
问题2:你能从图中估计出甲、乙两厂被抽查鸡腿平均质量吗?
请你写出甲、乙两厂被抽查鸡腿的平均质量,并在图中画出表示平均质量的直线.
问题3:观察两幅图表,看看被抽查的鸡腿质量的分布情况你有什么发现?
想一想
问题4:你能求出甲厂抽查的这20只鸡腿质量的最大值是多少吗?最小值又是多少?它们相差几克?乙厂呢?
问题5:现在你认为外贸公司应该购买哪个厂的鸡腿?为什么呢?
从图中看,甲厂的产品更符合要求.
甲厂鸡腿规格比较稳定,最大值和最小值只相差6
g;
乙厂鸡腿规格比较不稳定,最大值和最小值相差9
g.
现实生活中,除了关心数据的“平均水平”外,人们还关注数据的离散程度,即它们相对于平均水平的偏离情况.极差就是刻画数据离散程度的一个统计量.
定义
极差是指一组数据中最大数据与最小数据的差.
极差大,偏离平均数越大,产品的质量(性能)越不稳定.
如果丙厂也参与了竞争,从该厂也抽查20只鸡腿,
问题6:丙厂这20只鸡腿质量的平均数和极差分别是多少?
平均数:
极差:
想一想
问题7:在甲、丙两厂中,你认为外贸公司应该购买哪个
厂的鸡腿?
议一议
问题8:在甲、丙两厂中,写出每个鸡腿质量与平均数之间差的绝对值,你有什么发现?
平均数不能刻画数据的离散程度,而极差只能局部反映数据的离散程度.
为了从整体上反映数据的波动大小,办法不止一个:
①求各数据与其平均数的差距的和或平均数;
26.
甲厂:
丙厂:
36.
②求各数据与平均数之差的平方的平均数.
甲厂:
丙厂:
2.5.
4.4.
方差是各个数据与平均数差的平方的平均数.
其中,
是
的平均数,s2是方差.
标准差(s)是方差的算术平方根.
定义
注意:一般而言,一组数据的极差、方差或标准差越小,这组数据就越稳定.
1.据统计,某学校教师中年龄最大的为54岁,年龄最小
的为21岁.那么学校教师年龄的极差是
岁.
2.若一组数据的方差为0.16,那么这组数据的标准
差为
.
3.对甲.乙两个小麦品种各100株小麦的株高x(单位:m)进行测量,算出
于是可估计株高较整齐的小麦品种是________.
4.八年级某班的五个同学每人投掷铅球一次,测得成绩如下(单位:m):5,6,9,7,8,这组数据的方差是_______.
标准差是
________.
通过本课的学习,需要我们掌握:
1.刻画一组数据的离散程度可以用极差、方差、标准差这三种统计量表示.一组数据的极差、方差或标准差越小,这组数据就越稳定.
2.方差(标准差)比极差更能从整体上刻画数据的波动大小,是统计中最常用的统计量之一.
3.方差(标准差)的计算按公式进行.
3.4数据的离散程度(1)
第三章
数据的分析
1.了解刻画数据离散程度的三个量度——极差、方差和标准差的概念.
2.能借助计算器求极差、方差和标准差的数值,并在具体问题中加以应用.
3.经历表示数据离散程度的几个量的探索,体会用样本估计总体的思想.
练习一
1、某校八年级五个班的学生人数分别为:
54,56,49,51,50人.
求这五个班级的平均人数.
2、数据-1,0,1,
3
,
2,2,2,1的众数是
;中位数是
.
练习二
时代中学田径队的甲、乙两名运动员在8次百米跑训练中,成绩如下表:
序数
1
2
3
4
5
6
7
8
甲的成绩/秒
12.0
12.2
13.0
12.6
13.1
12.5
12.4
12.2
乙的成绩/秒
12.2
12.4
12.7
12.5
12.9
12.2
12.8
12.3
序数
平均数
中位数
众数
甲
乙
1、请同学们根据上表信息完成下表:
12.5
12.45
12.2
12.5
2、小亮说:“甲、乙两名运动员的训练成绩的平均数、中
位数、众数对应相同,
因此他们的成绩一样.”你认为这种
说法合适吗?
12.45
12.2
我国加入“WTO”后,为了提高农副产品的国际竞争力,一些行业协会对农副产品的规格进行了划分.
某外贸公司要出口一批规格为75
g的鸡腿,现有2个厂家提供货源,它们的价格相同,鸡腿品质相近.
质检员分别从甲、乙两厂的产品中抽样调查了20只鸡腿,质量(单位:g)如下:
甲厂:75
74
74
76
73
76
75
77
77
74
74
75
75
76
73
76
73
78
77
72
乙厂:75
78
72
77
74
75
73
79
72
75
80
71
76
77
73
78
71
76
73
75
问题1:如果只考虑鸡腿的规格,你认为外贸公司应该购买哪个厂的鸡腿?
问题2:你能从图中估计出甲、乙两厂被抽查鸡腿平均质量吗?
请你写出甲、乙两厂被抽查鸡腿的平均质量,并在图中画出表示平均质量的直线.
问题3:观察两幅图表,看看被抽查的鸡腿质量的分布情况你有什么发现?
想一想
问题4:你能求出甲厂抽查的这20只鸡腿质量的最大值是多少吗?最小值又是多少?它们相差几克?乙厂呢?
问题5:现在你认为外贸公司应该购买哪个厂的鸡腿?为什么呢?
从图中看,甲厂的产品更符合要求.
甲厂鸡腿规格比较稳定,最大值和最小值只相差6
g;
乙厂鸡腿规格比较不稳定,最大值和最小值相差9
g.
现实生活中,除了关心数据的“平均水平”外,人们还关注数据的离散程度,即它们相对于平均水平的偏离情况.极差就是刻画数据离散程度的一个统计量.
定义
极差是指一组数据中最大数据与最小数据的差.
极差大,偏离平均数越大,产品的质量(性能)越不稳定.
如果丙厂也参与了竞争,从该厂也抽查20只鸡腿,
问题6:丙厂这20只鸡腿质量的平均数和极差分别是多少?
平均数:
极差:
想一想
问题7:在甲、丙两厂中,你认为外贸公司应该购买哪个
厂的鸡腿?
议一议
问题8:在甲、丙两厂中,写出每个鸡腿质量与平均数之间差的绝对值,你有什么发现?
平均数不能刻画数据的离散程度,而极差只能局部反映数据的离散程度.
为了从整体上反映数据的波动大小,办法不止一个:
①求各数据与其平均数的差距的和或平均数;
26.
甲厂:
丙厂:
36.
②求各数据与平均数之差的平方的平均数.
甲厂:
丙厂:
2.5.
4.4.
方差是各个数据与平均数差的平方的平均数.
其中,
是
的平均数,s2是方差.
标准差(s)是方差的算术平方根.
定义
注意:一般而言,一组数据的极差、方差或标准差越小,这组数据就越稳定.
1.据统计,某学校教师中年龄最大的为54岁,年龄最小
的为21岁.那么学校教师年龄的极差是
岁.
2.若一组数据的方差为0.16,那么这组数据的标准
差为
.
3.对甲.乙两个小麦品种各100株小麦的株高x(单位:m)进行测量,算出
于是可估计株高较整齐的小麦品种是________.
4.八年级某班的五个同学每人投掷铅球一次,测得成绩如下(单位:m):5,6,9,7,8,这组数据的方差是_______.
标准差是
________.
通过本课的学习,需要我们掌握:
1.刻画一组数据的离散程度可以用极差、方差、标准差这三种统计量表示.一组数据的极差、方差或标准差越小,这组数据就越稳定.
2.方差(标准差)比极差更能从整体上刻画数据的波动大小,是统计中最常用的统计量之一.
3.方差(标准差)的计算按公式进行.
