八年级鲁教版(五四制)数学上册第二章分式与分式方程复习课件(17张PPT)
文档属性
| 名称 | 八年级鲁教版(五四制)数学上册第二章分式与分式方程复习课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 00:00:00 | ||
图片预览





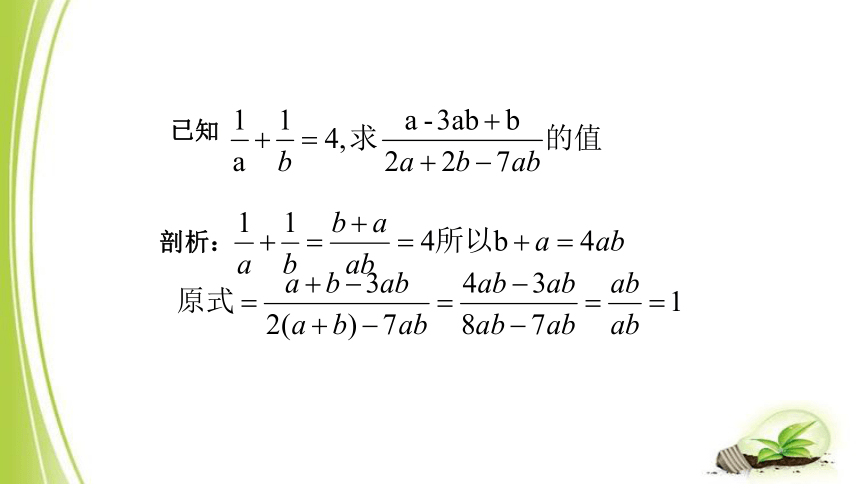
文档简介
(共17张PPT)
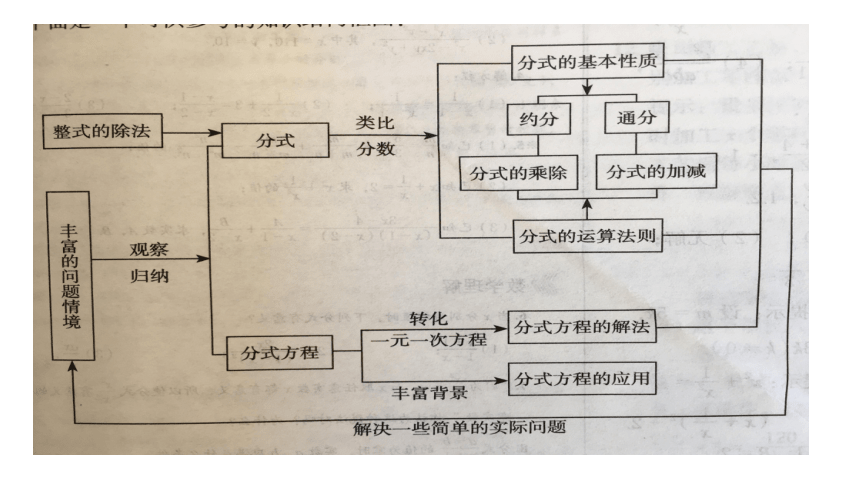
鲁教版八年级上册第二章
分式与分式方程复习
2、分式的基本性质:分式的分子与分母都乘以(或
除以)同一个不等于零的整式,分式的值不变。
3、分式的乘除法:两个分式相乘,把分子相乘的积
作为积的分子,把分母相乘的积作为积的分母;
两个分式相除,把除式的分子和分母颠倒位置后,
再与被除式相乘。结果要化为最简分式或整式。
1、形如
的式子叫做分式,其中A、B是整式,B
中必须含有字母。对于任意一个分式,分母都不
能为零。
基础知识回顾
4、分式的加减法:同分母的分式相加减,分母不变,
把分子相加减;异分母的分式相加减,先通分,
化为同分母的分式,然后再按同分母分式的加减
法则进行计算。
5、分式方程是分母中含有未知数的方程:解分式方
程的基本思想是把分式方程转化为整式方程,其
一般步骤是:去分母,解整式方程,验根。
当分式的分母不等于零时,分式有意义;当分式的
分子等于零,而分母不等于零时,分式的值为零。
当
x
取什么值时,分式
(1)有意义?
(2)值为零?
典例剖析
已知
,求
的值。
因为
,即x=2y
所以,原式
多字母消元法
已知
剖析:
考点
课标要求
难度
分式方程的概念
1.知道分式方程的概念,会识别分式方程;
2.理解分式方程中产生增根(无解)的情况.
较难
分式方程的解法
1.知道解分式方程的一般步骤;
2.掌握应用“去分母”将分式方程转化为整式方程,领会解分式方程“整式化”的化归思想;
3.掌握分式方程的验根方法,注意解分式方程时可能会出现增根,解方程后一定要验根.
中等
分式方程的应用
1.分式方程来解决简单的实际问题;
2.在列分式方程应用题求解检验时,不仅要考虑是否产生了增根,还要考虑是否符合题意(实际情况).
中等
下列方程中,哪些是分式方程?哪些整式方程?
整式方程
分式方程
练一练
1、解分式方程
一个“必须”是:必须
;
二个“基本”是:解分式方程的基本思想是
,
基本方法是
;
三个“步骤”是:
,
,
。
检验
转化
去分母
去分母
解整式方程
检验
解分式方程
解方程:
解:方程两边都乘(x2
-1
),得
x+1=2x
解这个方程,得x=1
检验:当x=1时,x2
-1
=0
所以x=1是原方程的增根,故原方程无解。
典例剖析
练一练
①
审
分析题意,找出等量关系。
②
设
选择恰当的未知数,注意单位。
③
列
根据等量关系正确列出方程。
④
解
认真仔细。
⑤
验
检验(是否是方程根和是否符合题意)
⑥
答
完整作答。
列方程解应用题的步骤:
分式方程的应用:
甲、乙两地相距19千米,王刚从甲地去乙地,
先步行了7千米,然后改骑自行车,共用了2小
时到达乙地,已知王刚骑自行车的速度是步行
速度的4倍,求他步行的速度和骑自行车的速
度。
典例剖析:
解:设步行的速度是
x
千米/小时,则骑自行车的
速度为
4x
千米/小时。根据题意,得
解这个方程,得
x
=
5
经检验
x
=
5
是所列方程的根,这时
4x=20
答:他步行的速度是
5千米/时,骑自行车的速度
是20千米/时。
4、华昌中学利源商场购进A、B两种品牌的足球,购买A品牌足球花费了2500元,购买B品牌足球花费了2000元,且购买A品牌足球数量是购买B品牌足球数量的2倍,已知购买一个B品牌足球比购买一个A品牌足球多花30元.求购买一个A品牌、一个B品牌的足球各需多少元?
这节课你有哪些收获?
小结
谢谢!
鲁教版八年级上册第二章
分式与分式方程复习
2、分式的基本性质:分式的分子与分母都乘以(或
除以)同一个不等于零的整式,分式的值不变。
3、分式的乘除法:两个分式相乘,把分子相乘的积
作为积的分子,把分母相乘的积作为积的分母;
两个分式相除,把除式的分子和分母颠倒位置后,
再与被除式相乘。结果要化为最简分式或整式。
1、形如
的式子叫做分式,其中A、B是整式,B
中必须含有字母。对于任意一个分式,分母都不
能为零。
基础知识回顾
4、分式的加减法:同分母的分式相加减,分母不变,
把分子相加减;异分母的分式相加减,先通分,
化为同分母的分式,然后再按同分母分式的加减
法则进行计算。
5、分式方程是分母中含有未知数的方程:解分式方
程的基本思想是把分式方程转化为整式方程,其
一般步骤是:去分母,解整式方程,验根。
当分式的分母不等于零时,分式有意义;当分式的
分子等于零,而分母不等于零时,分式的值为零。
当
x
取什么值时,分式
(1)有意义?
(2)值为零?
典例剖析
已知
,求
的值。
因为
,即x=2y
所以,原式
多字母消元法
已知
剖析:
考点
课标要求
难度
分式方程的概念
1.知道分式方程的概念,会识别分式方程;
2.理解分式方程中产生增根(无解)的情况.
较难
分式方程的解法
1.知道解分式方程的一般步骤;
2.掌握应用“去分母”将分式方程转化为整式方程,领会解分式方程“整式化”的化归思想;
3.掌握分式方程的验根方法,注意解分式方程时可能会出现增根,解方程后一定要验根.
中等
分式方程的应用
1.分式方程来解决简单的实际问题;
2.在列分式方程应用题求解检验时,不仅要考虑是否产生了增根,还要考虑是否符合题意(实际情况).
中等
下列方程中,哪些是分式方程?哪些整式方程?
整式方程
分式方程
练一练
1、解分式方程
一个“必须”是:必须
;
二个“基本”是:解分式方程的基本思想是
,
基本方法是
;
三个“步骤”是:
,
,
。
检验
转化
去分母
去分母
解整式方程
检验
解分式方程
解方程:
解:方程两边都乘(x2
-1
),得
x+1=2x
解这个方程,得x=1
检验:当x=1时,x2
-1
=0
所以x=1是原方程的增根,故原方程无解。
典例剖析
练一练
①
审
分析题意,找出等量关系。
②
设
选择恰当的未知数,注意单位。
③
列
根据等量关系正确列出方程。
④
解
认真仔细。
⑤
验
检验(是否是方程根和是否符合题意)
⑥
答
完整作答。
列方程解应用题的步骤:
分式方程的应用:
甲、乙两地相距19千米,王刚从甲地去乙地,
先步行了7千米,然后改骑自行车,共用了2小
时到达乙地,已知王刚骑自行车的速度是步行
速度的4倍,求他步行的速度和骑自行车的速
度。
典例剖析:
解:设步行的速度是
x
千米/小时,则骑自行车的
速度为
4x
千米/小时。根据题意,得
解这个方程,得
x
=
5
经检验
x
=
5
是所列方程的根,这时
4x=20
答:他步行的速度是
5千米/时,骑自行车的速度
是20千米/时。
4、华昌中学利源商场购进A、B两种品牌的足球,购买A品牌足球花费了2500元,购买B品牌足球花费了2000元,且购买A品牌足球数量是购买B品牌足球数量的2倍,已知购买一个B品牌足球比购买一个A品牌足球多花30元.求购买一个A品牌、一个B品牌的足球各需多少元?
这节课你有哪些收获?
小结
谢谢!
