八年级鲁教版(五四制)数学上册课件:5.2平行四边形的判定第3课时(18张ppt)
文档属性
| 名称 | 八年级鲁教版(五四制)数学上册课件:5.2平行四边形的判定第3课时(18张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 176.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 15:57:58 | ||
图片预览


文档简介
(共18张PPT)
5.2平行四边形的判定(3)
八年级上册第五章
平行四边形
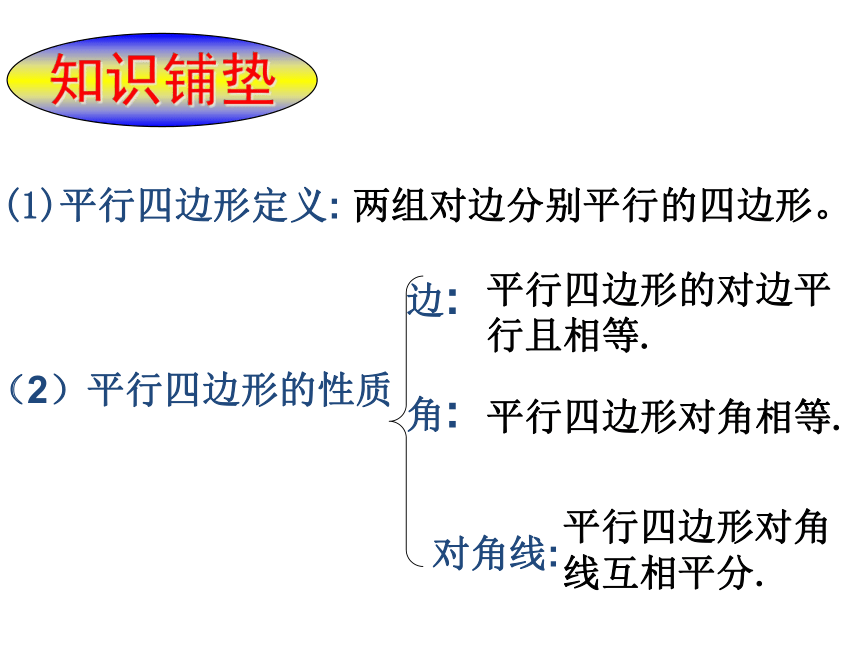
角:
边:
(2)平行四边形的性质
(1)平行四边形定义:
平行四边形的对边平
行且相等.
平行四边形对角相等.
知识铺垫
两组对边分别平行的四边形。
平行四边形对角
线互相平分.
对角线:
判定
文字语言
图形语言
符号语言
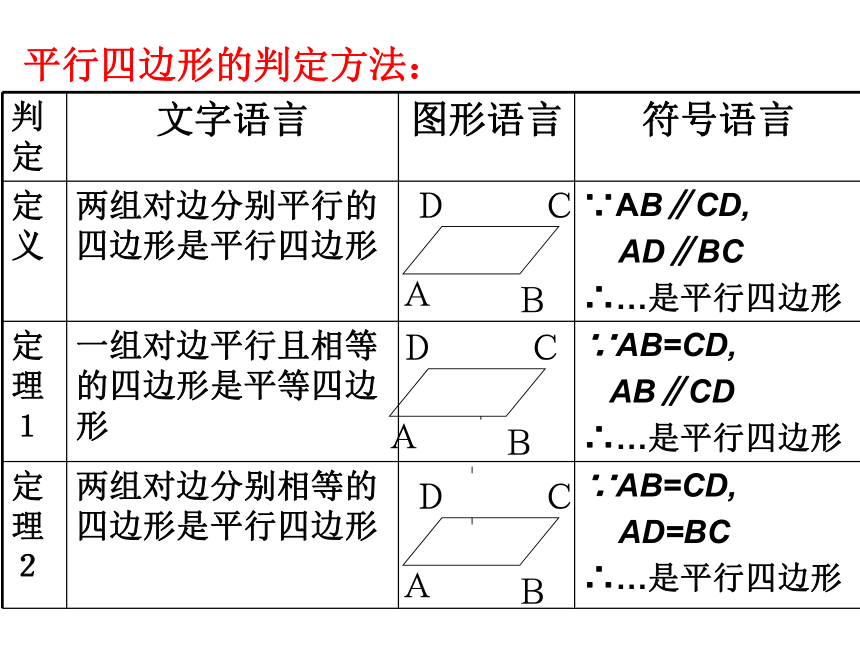
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是平行四边形
定理1
一组对边平行且相等的四边形是平等四边形
∵AB=CD,
AB∥CD
∴…是平行四边形
定理2
两组对边分别相等的四边形是平行四边形
∵AB=CD,
AD=BC
∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
平行四边形的判定方法:
1.熟记平行四边形的判定定理3,并会进行证明;
2.会在实际问题中灵活应用平行四边形的判定定理1、2,3进行计算和证明。
教学目标
D
B
A
C
O
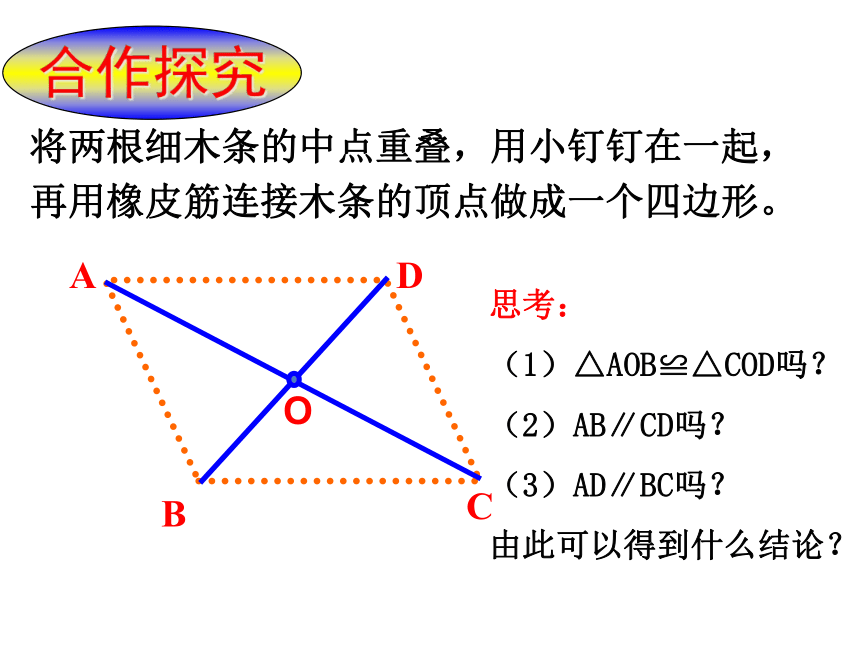
将两根细木条的中点重叠,用小钉钉在一起,
再用橡皮筋连接木条的顶点做成一个四边形。
思考:
(1)△AOB≌△COD吗?
(2)AB∥CD吗?
(3)AD∥BC吗?
由此可以得到什么结论?
合作探究
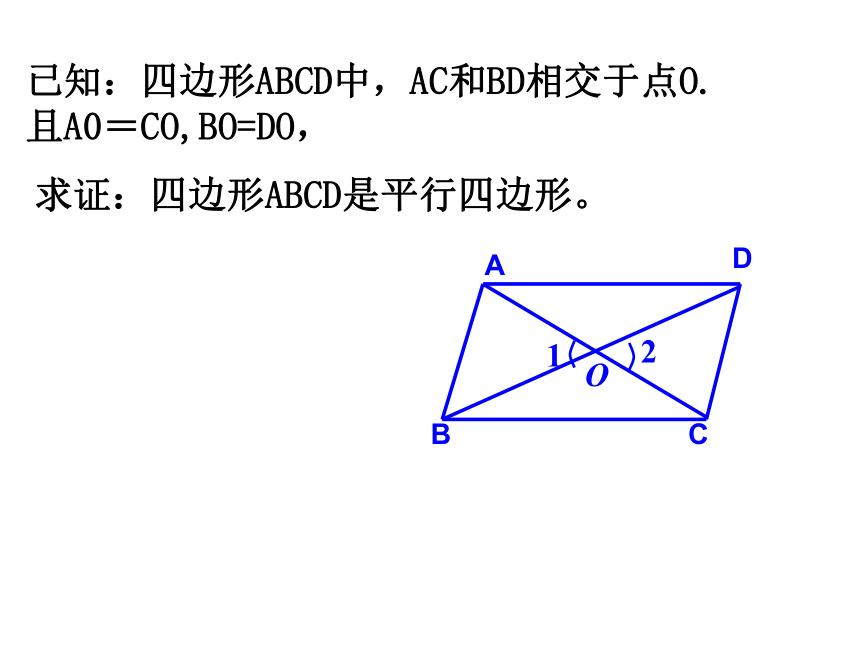
已知:四边形ABCD中,AC和BD相交于点O.
且A0=CO,BO=DO,
求证:四边形ABCD是平行四边形。
A
B
D
C
O
1
2
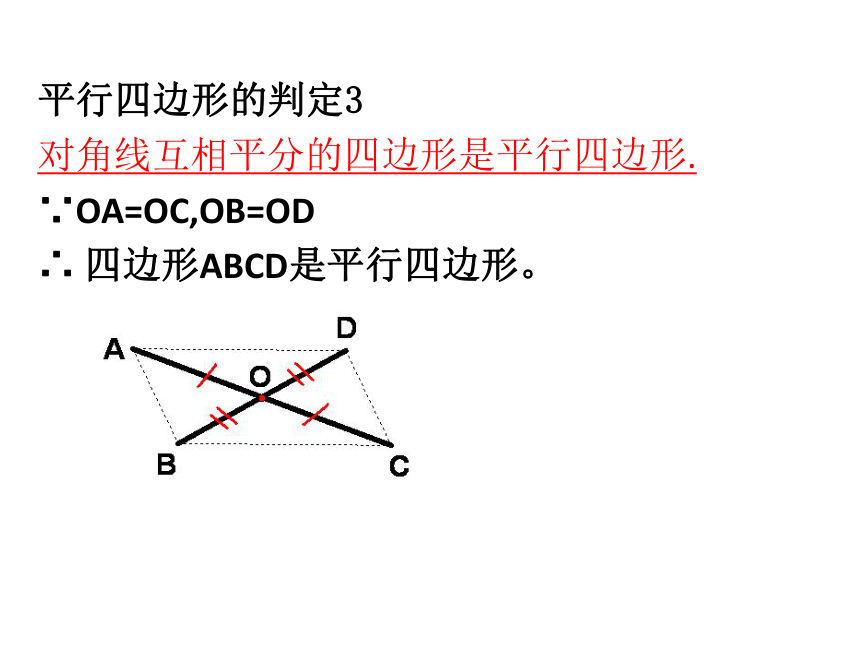
平行四边形的判定3
对角线互相平分的四边形是平行四边形.
∵OA=OC,OB=OD
∴
四边形ABCD是平行四边形。
知识应用:
已知:如图,把△ABC的中线AD延长至E,使得DE=AD,连结EB,EC,求证:四边形ABEC是平行四边形.
例题引领
例2
变式训练:
已知:如图,在
ABCD中,E,F是对角线BD上的两点,且AE//
CF.
求证:四边形AECF是平行四边形
F
E
D
C
B
A
O
知识应用:
1.
2.如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.
3.如图,在
ABCD中,EF过对角线交点O,分别交AD,BC于点E,F,点G,H分别是OA与OC的中点,试判断四边形EGFH的形状,并证明你的结论.
4.如图,在平行四边形ABCD中,过对角线的交点O作两条直线分别与AB,BC,CD,DA交于点G,F,H,E,求证:四边形GFHE是平行四边形。
A
H
F
E
D
C
B
G
O
5.如图,在平行四边形ABCD中,点E是CD的的中点,AE的延长线与BC交于点F。(1)求证:ΔAED≌ΔFEC;
(2)连接AC、DF,求证四边形ACFD是平行四边形。
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
系统总结
当堂达标
见导学案。
布置作业
课本:
习题5.2 5题、6题
5.2平行四边形的判定(3)
八年级上册第五章
平行四边形
角:
边:
(2)平行四边形的性质
(1)平行四边形定义:
平行四边形的对边平
行且相等.
平行四边形对角相等.
知识铺垫
两组对边分别平行的四边形。
平行四边形对角
线互相平分.
对角线:
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是平行四边形
定理1
一组对边平行且相等的四边形是平等四边形
∵AB=CD,
AB∥CD
∴…是平行四边形
定理2
两组对边分别相等的四边形是平行四边形
∵AB=CD,
AD=BC
∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
平行四边形的判定方法:
1.熟记平行四边形的判定定理3,并会进行证明;
2.会在实际问题中灵活应用平行四边形的判定定理1、2,3进行计算和证明。
教学目标
D
B
A
C
O
将两根细木条的中点重叠,用小钉钉在一起,
再用橡皮筋连接木条的顶点做成一个四边形。
思考:
(1)△AOB≌△COD吗?
(2)AB∥CD吗?
(3)AD∥BC吗?
由此可以得到什么结论?
合作探究
已知:四边形ABCD中,AC和BD相交于点O.
且A0=CO,BO=DO,
求证:四边形ABCD是平行四边形。
A
B
D
C
O
1
2
平行四边形的判定3
对角线互相平分的四边形是平行四边形.
∵OA=OC,OB=OD
∴
四边形ABCD是平行四边形。
知识应用:
已知:如图,把△ABC的中线AD延长至E,使得DE=AD,连结EB,EC,求证:四边形ABEC是平行四边形.
例题引领
例2
变式训练:
已知:如图,在
ABCD中,E,F是对角线BD上的两点,且AE//
CF.
求证:四边形AECF是平行四边形
F
E
D
C
B
A
O
知识应用:
1.
2.如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.
3.如图,在
ABCD中,EF过对角线交点O,分别交AD,BC于点E,F,点G,H分别是OA与OC的中点,试判断四边形EGFH的形状,并证明你的结论.
4.如图,在平行四边形ABCD中,过对角线的交点O作两条直线分别与AB,BC,CD,DA交于点G,F,H,E,求证:四边形GFHE是平行四边形。
A
H
F
E
D
C
B
G
O
5.如图,在平行四边形ABCD中,点E是CD的的中点,AE的延长线与BC交于点F。(1)求证:ΔAED≌ΔFEC;
(2)连接AC、DF,求证四边形ACFD是平行四边形。
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
系统总结
当堂达标
见导学案。
布置作业
课本:
习题5.2 5题、6题
