2021—2022学年沪科版数学九年级上册_22.2相似三角形判定 综合课件(共24张PPT)
文档属性
| 名称 | 2021—2022学年沪科版数学九年级上册_22.2相似三角形判定 综合课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 307.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
22.2
相似三角形的判定
第五课时
相似三角形的判定综合练习
沪科版数学九年级上
相似三角形的判定方法
定理1
两角对应相等的两个三角形相似.
推论1
平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;
定理2
三边对应成比例的两个三角形相似.
定理3
两边对应成比例,且夹角相等的两个三角形相似;
定理4
斜边直角边对应成比例的两个直角三角形相似.
复习
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
O
C
D
A
B
A
B
C
D
E
B
D
A
C
1
2
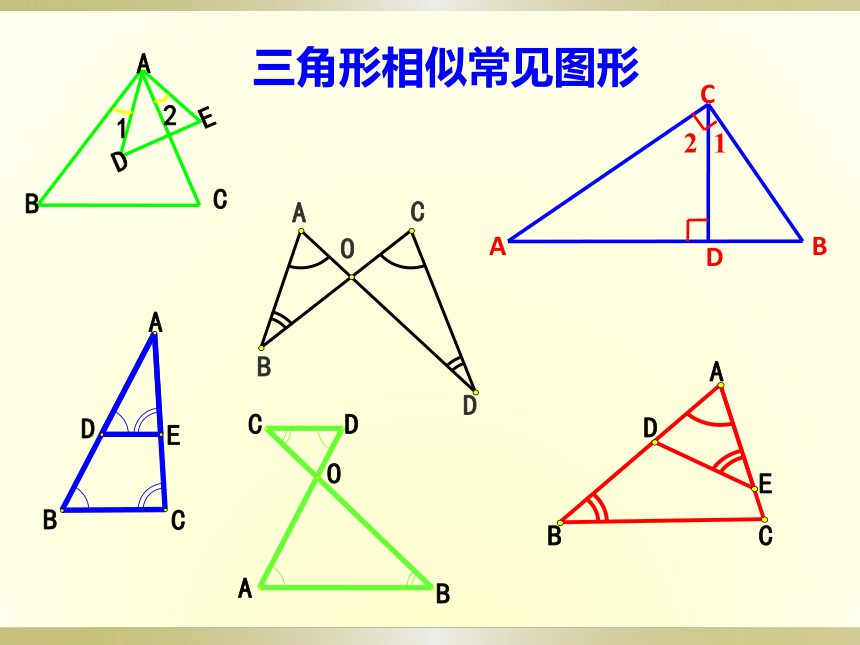
三角形相似常见图形
基础练习
1.如图,P是AB上一点,补充下列条件:
(1)
∠ACP=∠B;
(2)∠APC=∠ACB;
其中一定能使△
ACP∽
△ABC的是(
)
(A)
(1)
(2)
(3)
(4)
(B)
(1)
(2)
(3)
(C)
(3)
(D)
(1)
(2)
(4)
A
B
C
P
D
2.
图中的两个三角形是否相似?
15
25
20
27
45
40
A
B
C
D
E
45
54
36
30
∠ACB=∠ECD
∴△ACB∽△ECD
对应边的比不相等
∴图中两个三角形不相似.
解:(1)
(2)
3、
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A.1.25尺 B.57.5尺 C.6.25尺 D.56.5尺
B
4、为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )
A.10m B.12m C.12.4m
D.12.32m
B
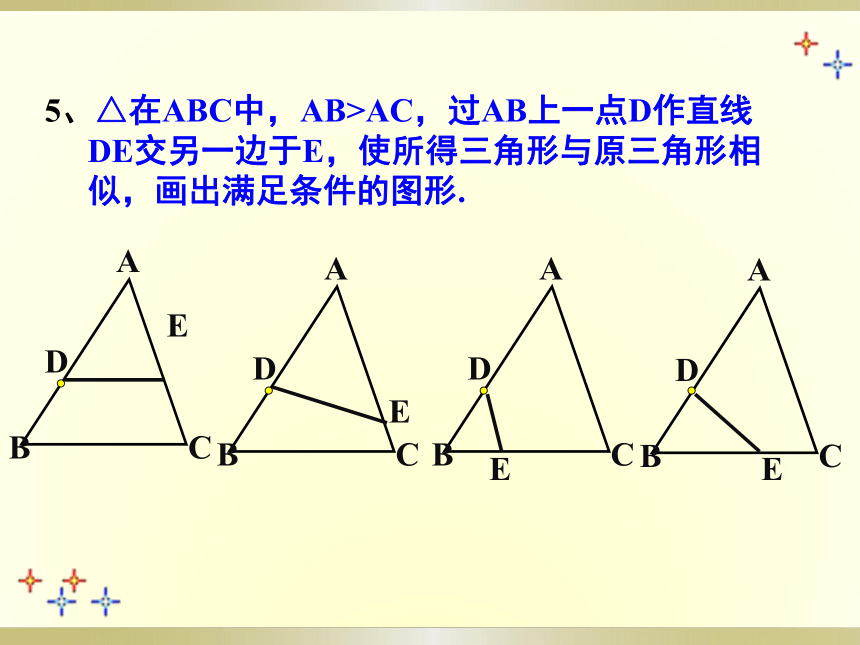
5、△在ABC中,AB>AC,过AB上一点D作直线DE交另一边于E,使所得三角形与原三角形相似,画出满足条件的图形.
E
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
E
E
E
提升练习一
1、如图,AE=4cm,AD=3cm,DE=2.4cm,BD=2cm,CE=
cm,求BC的长.
∵
∠A=
∠A,
∴△ADE∽△ABC.
解:
A
E
C
D
B
解:设正方形的边长为x,
则AD=AC-x=7.5-x,BF=BC-x=5-x,
又由题意可知△ADE∽△EFB
得x=3
即正方形的边长为3.
则:
A
E
B
F
C
D
2.如图,在Rt△ABC中,
∠C=90°.正方形EFCD的三个顶点E,F,D分别在边AB,BC,AC上.已知AC=7.5,BC=5,求正方形的边长.
4、如图,∠APD=900,AP=PB=BC=CD,则下列结论成立的是(
)
A
ΔPAB∽ΔPCA
B
ΔPAB∽ΔPDA
C
ΔABC
∽
ΔDBA
D
ΔABC∽ΔDCA
C
A
B
P
C
D
5.已知,AB∥CD∥EF,
(1)图中有几对相似的三角形?
(2)线段AB、CD与EF有怎样的等量关系?
F
A
B
C
D
E
⊿EDC∽⊿EBA
⊿ADC∽⊿AFE
⊿BDA∽⊿EDF
如图,
在RtΔABC中,CD是斜边AB上的高。求证:BC2+AC2
=AB2.
证明:
∵∠ACB=∠ADC=90°
∴
AC2=AD·AB,
∴
BC2=BD·BA
∴△ACD∽△ABC
同理:
△ABC∽△CBD
B
D
A
C
1
2
∠A=∠A
6.你能根据相似形知识证明勾股定理吗?
∴BC2+AC2=AB·BD+AB·AD
=AB(BD+AD)
=AB2.
即:BC2+AC2
=AB2.
拓展练习
1、如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,P是Rt△ABC的重心,求P点到AB所在直线的距离
C
A
B
P
D
E
F
解:连结CP并延长交AB于D点,连结BP并延长至F交AC于E,使得PE=EF,连结AF
∵P是Rt△ABC的重心
∴CD⊥AB,且AD=DB=3
CE=AE
易得:
△AFE
≌△CPE
∴∠FAD=90°,CP=AF=CD-PD
∴AF∥PD
∴AF:PD=AB:BD
∴(3-PD):PD=AB:BD=2:1
∴PD=1
2、△ABC中,∠
BAC是直角,过斜边中点M而垂直于
斜边BC的直线交CA的延长线于E,
交AB于D,连AM.
求证:AM2=MD
·
ME
证明:①∵∠BAC=90°
M为斜边BC中点
∴AM=BM=BC/2
∴
∠B=
∠MAD
又
∵
∠B+
∠BDM=90°
∠E+
∠ADE=
90°
∠BDM=
∠ADE
∴∠B=∠E
∴∠MAD=
∠E
又
∵
∠DMA=
∠AME
∴△MAD∽
△MEA
A
B
M
C
D
E
∴AM2=MD
·
ME
3.如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,
求证:ED2=EO
·
EC.
证明:∵
AB∥CD
∴
∠C=∠A
∵
AO=OB,DF=FB
∴
∠A=
∠B,
∠B=
∠FDB
∴
∠C=
∠FDB
又
∵
∠DEO=
∠DEC
∴
△EDC∽△EOD
∴
,
即
ED2=EO
·
EC
ED
EO
=
EC
ED
4、如图,点C、D在线段AB上,且ΔPCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时ΔACP∽ΔPDB
(2)当ΔPDB∽ΔACP时,试求∠APB的度数.
C
D
B
P
A
你能行!
5、D为△ABC的底边BC的延长线上一点,直线DF
交AC于E,且∠FEA=∠AFE
.求证:BD·CE=CD·BF
F
E
D
C
B
A
作辅助线构造相似三角形
一题多解
试一试
5、D为△ABC的底边BC的延长线上一点,直线DF
交AC于E,且∠FEA=∠AFE
.求证:BD·CE=CD·BF
F
E
D
C
B
A
G
方法一:
过点C作CG∥AB,交DF于G
则△DCG∽
△DBF
F
E
D
C
B
A
G
故
5、.D为△ABC的底边BC的延长线上一点,直线DF
交AC于E,且∠FEA=∠AFE
.求证BD·CE=CD·BF
BD
BF
FG
CD
=
方法二:
过点C作CG∥DF,交AB于G
F
E
D
C
B
A
G
5、.D为△ABC的底边BC的延长线上一点,直线DF
交AC于E,且∠FEA=∠AF.求证:BD·CE=CD·BF
方法三:
过点B作BG∥DF,
交DF的延长线于G
22.2
相似三角形的判定
第五课时
相似三角形的判定综合练习
沪科版数学九年级上
相似三角形的判定方法
定理1
两角对应相等的两个三角形相似.
推论1
平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;
定理2
三边对应成比例的两个三角形相似.
定理3
两边对应成比例,且夹角相等的两个三角形相似;
定理4
斜边直角边对应成比例的两个直角三角形相似.
复习
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
O
C
D
A
B
A
B
C
D
E
B
D
A
C
1
2
三角形相似常见图形
基础练习
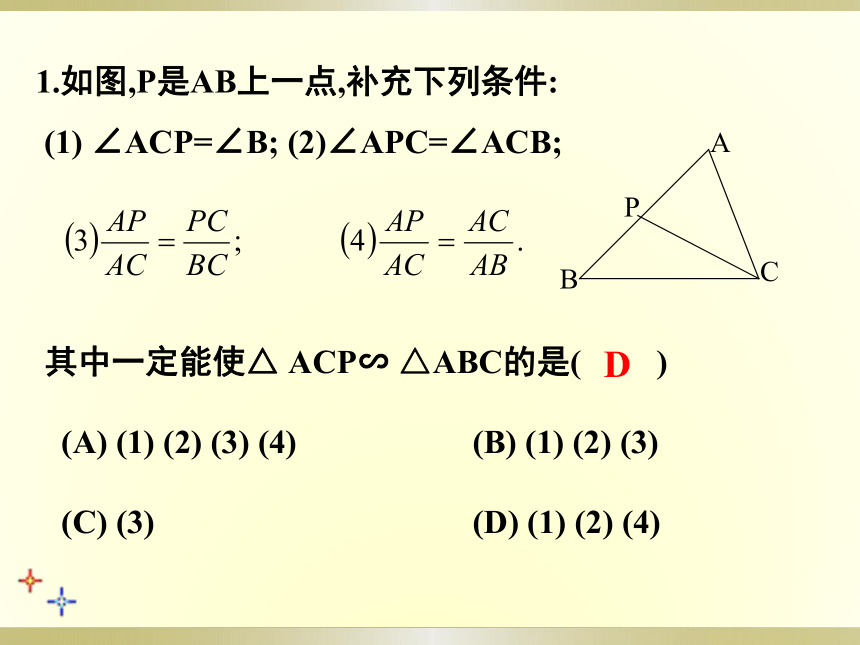
1.如图,P是AB上一点,补充下列条件:
(1)
∠ACP=∠B;
(2)∠APC=∠ACB;
其中一定能使△
ACP∽
△ABC的是(
)
(A)
(1)
(2)
(3)
(4)
(B)
(1)
(2)
(3)
(C)
(3)
(D)
(1)
(2)
(4)
A
B
C
P
D
2.
图中的两个三角形是否相似?
15
25
20
27
45
40
A
B
C
D
E
45
54
36
30
∠ACB=∠ECD
∴△ACB∽△ECD
对应边的比不相等
∴图中两个三角形不相似.
解:(1)
(2)
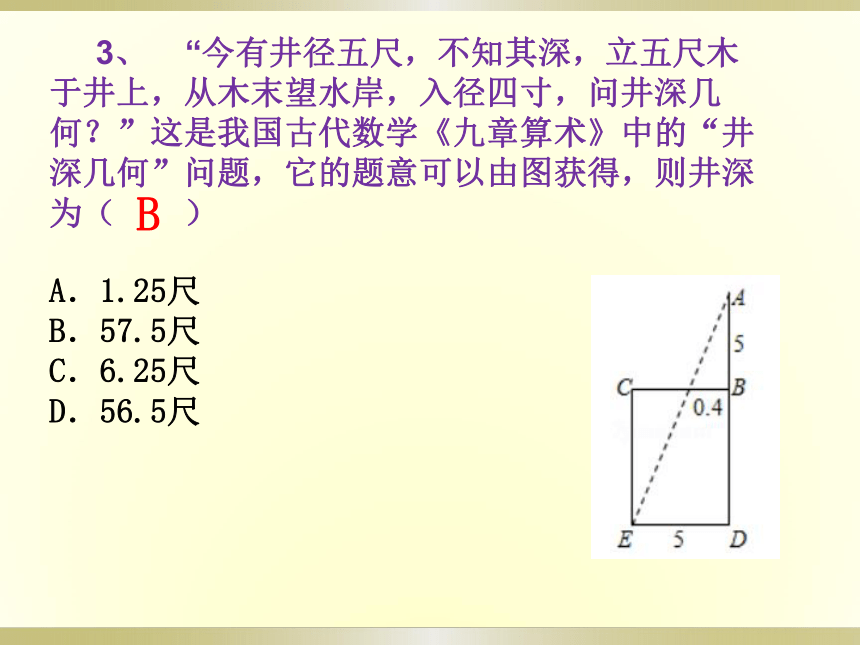
3、
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A.1.25尺 B.57.5尺 C.6.25尺 D.56.5尺
B
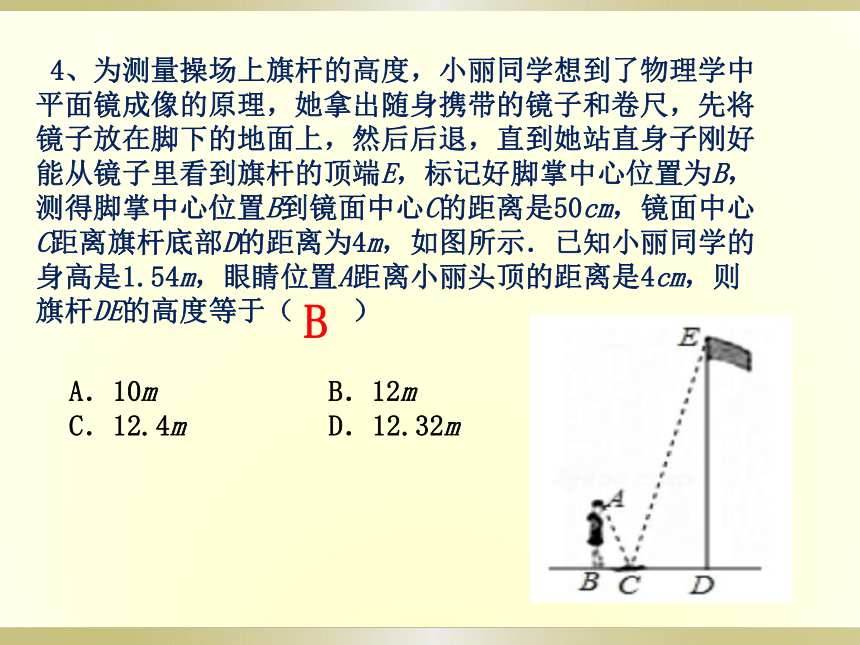
4、为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )
A.10m B.12m C.12.4m
D.12.32m
B
5、△在ABC中,AB>AC,过AB上一点D作直线DE交另一边于E,使所得三角形与原三角形相似,画出满足条件的图形.
E
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
E
E
E
提升练习一
1、如图,AE=4cm,AD=3cm,DE=2.4cm,BD=2cm,CE=
cm,求BC的长.
∵
∠A=
∠A,
∴△ADE∽△ABC.
解:
A
E
C
D
B
解:设正方形的边长为x,
则AD=AC-x=7.5-x,BF=BC-x=5-x,
又由题意可知△ADE∽△EFB
得x=3
即正方形的边长为3.
则:
A
E
B
F
C
D
2.如图,在Rt△ABC中,
∠C=90°.正方形EFCD的三个顶点E,F,D分别在边AB,BC,AC上.已知AC=7.5,BC=5,求正方形的边长.
4、如图,∠APD=900,AP=PB=BC=CD,则下列结论成立的是(
)
A
ΔPAB∽ΔPCA
B
ΔPAB∽ΔPDA
C
ΔABC
∽
ΔDBA
D
ΔABC∽ΔDCA
C
A
B
P
C
D
5.已知,AB∥CD∥EF,
(1)图中有几对相似的三角形?
(2)线段AB、CD与EF有怎样的等量关系?
F
A
B
C
D
E
⊿EDC∽⊿EBA
⊿ADC∽⊿AFE
⊿BDA∽⊿EDF
如图,
在RtΔABC中,CD是斜边AB上的高。求证:BC2+AC2
=AB2.
证明:
∵∠ACB=∠ADC=90°
∴
AC2=AD·AB,
∴
BC2=BD·BA
∴△ACD∽△ABC
同理:
△ABC∽△CBD
B
D
A
C
1
2
∠A=∠A
6.你能根据相似形知识证明勾股定理吗?
∴BC2+AC2=AB·BD+AB·AD
=AB(BD+AD)
=AB2.
即:BC2+AC2
=AB2.
拓展练习
1、如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,P是Rt△ABC的重心,求P点到AB所在直线的距离
C
A
B
P
D
E
F
解:连结CP并延长交AB于D点,连结BP并延长至F交AC于E,使得PE=EF,连结AF
∵P是Rt△ABC的重心
∴CD⊥AB,且AD=DB=3
CE=AE
易得:
△AFE
≌△CPE
∴∠FAD=90°,CP=AF=CD-PD
∴AF∥PD
∴AF:PD=AB:BD
∴(3-PD):PD=AB:BD=2:1
∴PD=1
2、△ABC中,∠
BAC是直角,过斜边中点M而垂直于
斜边BC的直线交CA的延长线于E,
交AB于D,连AM.
求证:AM2=MD
·
ME
证明:①∵∠BAC=90°
M为斜边BC中点
∴AM=BM=BC/2
∴
∠B=
∠MAD
又
∵
∠B+
∠BDM=90°
∠E+
∠ADE=
90°
∠BDM=
∠ADE
∴∠B=∠E
∴∠MAD=
∠E
又
∵
∠DMA=
∠AME
∴△MAD∽
△MEA
A
B
M
C
D
E
∴AM2=MD
·
ME
3.如图,AB∥CD,AO=OB,DF=FB,DF交AC于E,
求证:ED2=EO
·
EC.
证明:∵
AB∥CD
∴
∠C=∠A
∵
AO=OB,DF=FB
∴
∠A=
∠B,
∠B=
∠FDB
∴
∠C=
∠FDB
又
∵
∠DEO=
∠DEC
∴
△EDC∽△EOD
∴
,
即
ED2=EO
·
EC
ED
EO
=
EC
ED
4、如图,点C、D在线段AB上,且ΔPCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时ΔACP∽ΔPDB
(2)当ΔPDB∽ΔACP时,试求∠APB的度数.
C
D
B
P
A
你能行!
5、D为△ABC的底边BC的延长线上一点,直线DF
交AC于E,且∠FEA=∠AFE
.求证:BD·CE=CD·BF
F
E
D
C
B
A
作辅助线构造相似三角形
一题多解
试一试
5、D为△ABC的底边BC的延长线上一点,直线DF
交AC于E,且∠FEA=∠AFE
.求证:BD·CE=CD·BF
F
E
D
C
B
A
G
方法一:
过点C作CG∥AB,交DF于G
则△DCG∽
△DBF
F
E
D
C
B
A
G
故
5、.D为△ABC的底边BC的延长线上一点,直线DF
交AC于E,且∠FEA=∠AFE
.求证BD·CE=CD·BF
BD
BF
FG
CD
=
方法二:
过点C作CG∥DF,交AB于G
F
E
D
C
B
A
G
5、.D为△ABC的底边BC的延长线上一点,直线DF
交AC于E,且∠FEA=∠AF.求证:BD·CE=CD·BF
方法三:
过点B作BG∥DF,
交DF的延长线于G
