八年级鲁教版(五四制)数学上册课件:5.2平行四边形的判定(第2课时16张ppt)
文档属性
| 名称 | 八年级鲁教版(五四制)数学上册课件:5.2平行四边形的判定(第2课时16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 387.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 15:59:17 | ||
图片预览



文档简介
(共16张PPT)
八年级上册第五章
平行四边形
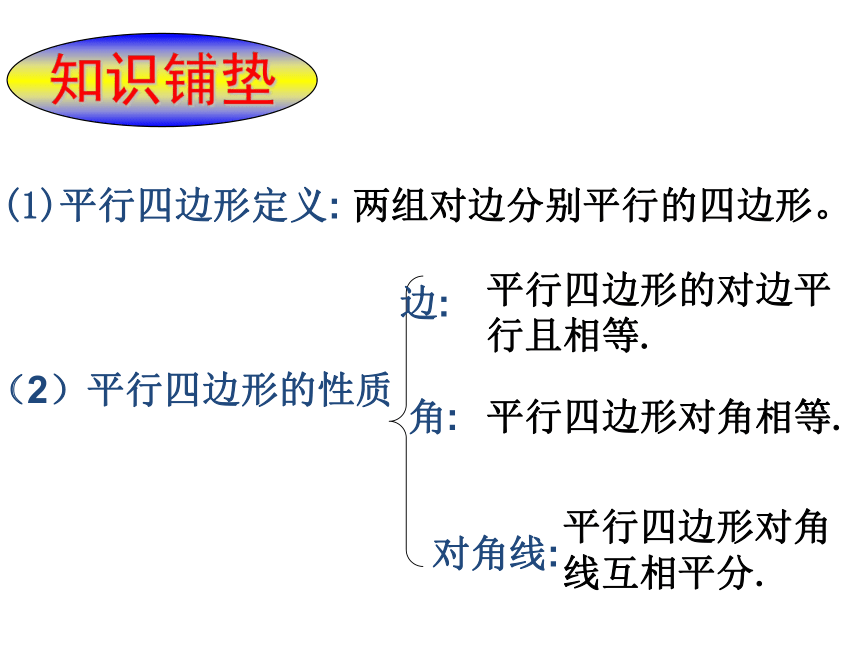
角:
边:
(2)平行四边形的性质
(1)平行四边形定义:
平行四边形的对边平
行且相等.
平行四边形对角相等.
知识铺垫
两组对边分别平行的四边形。
平行四边形对角
线互相平分.
对角线:
1.理解并掌握平行四边形的定义;
2.掌握平行四边形的判定定理2及其应用。
教学目标
按如下方法作图:先画出两条平行线
l1
,
l2
,然后在
l1
,
l2
上分别截取两条相等线段AD=BC,连接AB,CD,得到四边形ABCD.
观察你得到的四边形,你猜测它是平行四边形吗?能证明你的猜测是正确的吗?
l
2
l
1
C
A
D
B
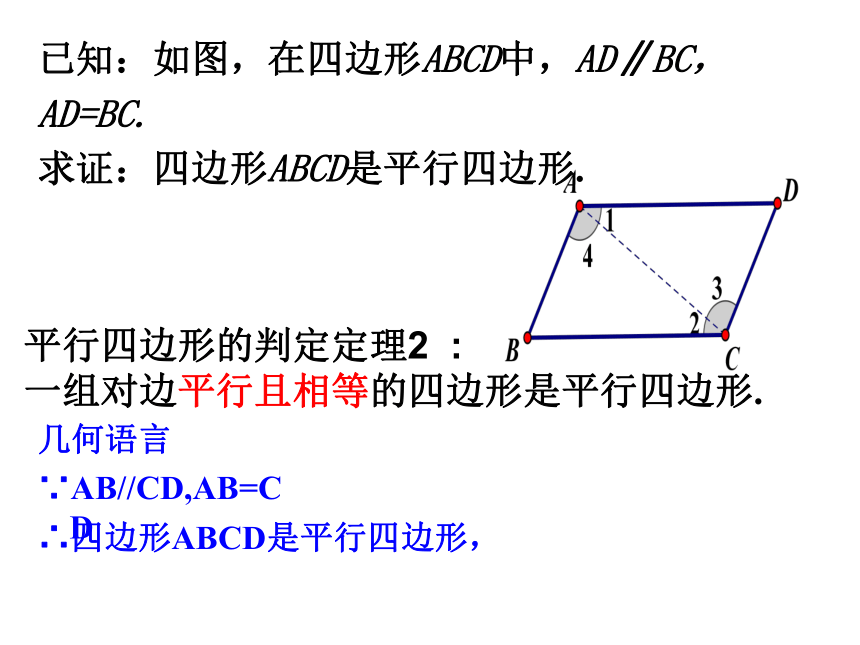
平行四边形的判定定理2
:
一组对边平行且相等的四边形是平行四边形.
已知:如图,在四边形ABCD中,AD∥BC,AD=BC.
求证:四边形ABCD是平行四边形.
几何语言
∵AB//CD,AB=CD
∴四边形ABCD是平行四边形,
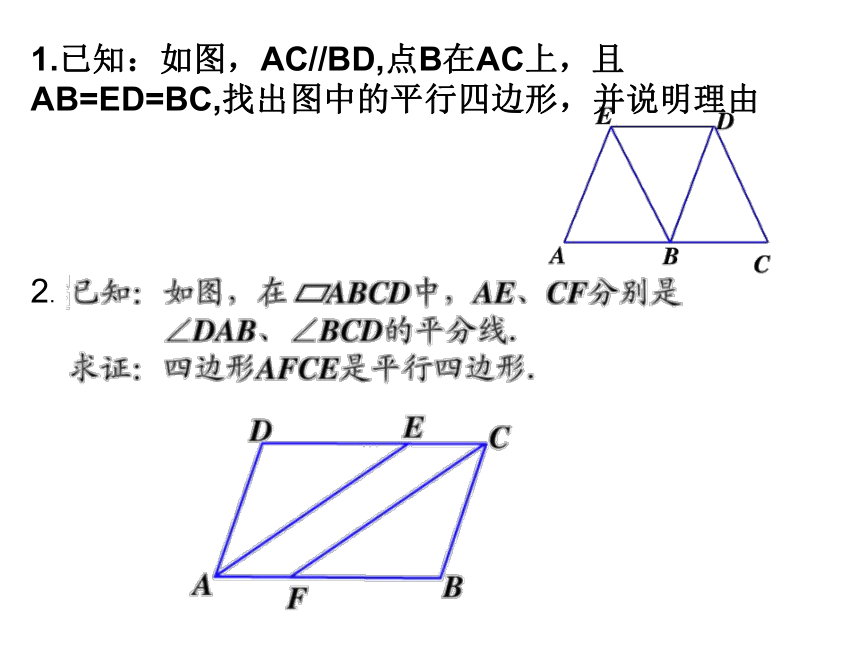
1.已知:如图,AC//BD,点B在AC上,且AB=ED=BC,找出图中的平行四边形,并说明理由
2.
3.
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是平行四边形
定理1
两组对边分别相等的四边形是平行四边形
∵AB=CD,
AD=BC
∴…是平行四边形
定理2
一组对边平行且相等的四边形是平等四边形
∵AB=CD,
AB∥CD
∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
平行四边形的判定方法:
1.如图,在四边形ABCD中,E是BC边的中点,连结D,E并延长,交AB的延长线于F点,AB=BF.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是(
)
A.AD=BC
B.CD=BF
C.∠A=∠C
D.∠F=∠CDE
知识应用:
2.已知:如图平行四边形ABCD中,E、F分别是AC上两点且BE⊥AC于E,DE⊥AC于F.求证:四边形BEDF是平行四边形
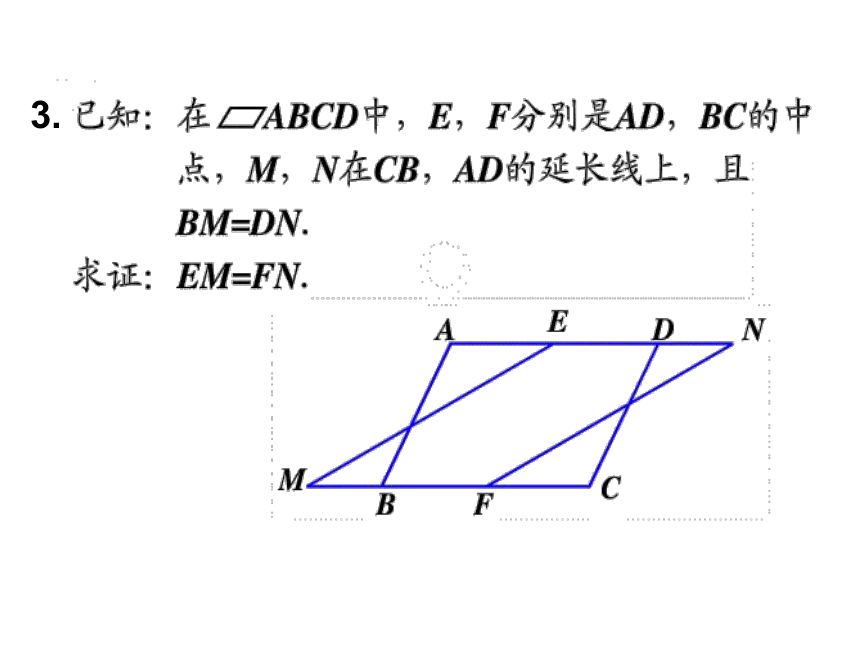
3.已知:平行四边形ABCD中,E,F分别是边AD,BC的中点,
求证:EB=DF
。
∴EB=DF
4.已知:平行四边形ABCD中,E,F分别是边BC和AD上点,且BE=DF,求证:四边形AECF是平行四边形。
F
D
E
C
B
A
5.已知:如图,平行四边形ABCD中,点E,F分别在AD和BC上的点,且AE=CF,BD,EF交于点O,求证EF与BD互相平分.
E
A
C
F
B
D
O
如图,在四边形ABCD中
⑴若∠A=100°,∠B=80°,
∠C=100°,∠D=80°,
则四边形ABCD是平行四边形吗?
为什么?
⑵若∠A=120°,∠B=60°,∠C=120°,∠D=60°,则四边形ABCD是平行四边形吗?为什么?
⑶若∠A=χ°,∠B=y°,∠C=χ°,∠D=y°,则四边形ABCD是平行四边形吗?为什么?
综上可知,当∠A与∠C,∠B与∠D分别满足什么关系时,四边形ABCD是平行四边形?
阅读思考题
A
D
B
C
当堂达标
见导学案。
布置作业
课本P15:
习题6.2 1题、2题
八年级上册第五章
平行四边形
角:
边:
(2)平行四边形的性质
(1)平行四边形定义:
平行四边形的对边平
行且相等.
平行四边形对角相等.
知识铺垫
两组对边分别平行的四边形。
平行四边形对角
线互相平分.
对角线:
1.理解并掌握平行四边形的定义;
2.掌握平行四边形的判定定理2及其应用。
教学目标
按如下方法作图:先画出两条平行线
l1
,
l2
,然后在
l1
,
l2
上分别截取两条相等线段AD=BC,连接AB,CD,得到四边形ABCD.
观察你得到的四边形,你猜测它是平行四边形吗?能证明你的猜测是正确的吗?
l
2
l
1
C
A
D
B
平行四边形的判定定理2
:
一组对边平行且相等的四边形是平行四边形.
已知:如图,在四边形ABCD中,AD∥BC,AD=BC.
求证:四边形ABCD是平行四边形.
几何语言
∵AB//CD,AB=CD
∴四边形ABCD是平行四边形,
1.已知:如图,AC//BD,点B在AC上,且AB=ED=BC,找出图中的平行四边形,并说明理由
2.
3.
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是平行四边形
定理1
两组对边分别相等的四边形是平行四边形
∵AB=CD,
AD=BC
∴…是平行四边形
定理2
一组对边平行且相等的四边形是平等四边形
∵AB=CD,
AB∥CD
∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
平行四边形的判定方法:
1.如图,在四边形ABCD中,E是BC边的中点,连结D,E并延长,交AB的延长线于F点,AB=BF.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是(
)
A.AD=BC
B.CD=BF
C.∠A=∠C
D.∠F=∠CDE
知识应用:
2.已知:如图平行四边形ABCD中,E、F分别是AC上两点且BE⊥AC于E,DE⊥AC于F.求证:四边形BEDF是平行四边形
3.已知:平行四边形ABCD中,E,F分别是边AD,BC的中点,
求证:EB=DF
。
∴EB=DF
4.已知:平行四边形ABCD中,E,F分别是边BC和AD上点,且BE=DF,求证:四边形AECF是平行四边形。
F
D
E
C
B
A
5.已知:如图,平行四边形ABCD中,点E,F分别在AD和BC上的点,且AE=CF,BD,EF交于点O,求证EF与BD互相平分.
E
A
C
F
B
D
O
如图,在四边形ABCD中
⑴若∠A=100°,∠B=80°,
∠C=100°,∠D=80°,
则四边形ABCD是平行四边形吗?
为什么?
⑵若∠A=120°,∠B=60°,∠C=120°,∠D=60°,则四边形ABCD是平行四边形吗?为什么?
⑶若∠A=χ°,∠B=y°,∠C=χ°,∠D=y°,则四边形ABCD是平行四边形吗?为什么?
综上可知,当∠A与∠C,∠B与∠D分别满足什么关系时,四边形ABCD是平行四边形?
阅读思考题
A
D
B
C
当堂达标
见导学案。
布置作业
课本P15:
习题6.2 1题、2题
