2021-2022学年教科版(2019)必修第一册 2.2匀变速直线运动速度与时间的关系 课件(46张PPT)
文档属性
| 名称 | 2021-2022学年教科版(2019)必修第一册 2.2匀变速直线运动速度与时间的关系 课件(46张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-20 16:27:51 | ||
图片预览









文档简介
(共46张PPT)
2.匀变速直线运动速度与时间的关系
必备知识·自主学习
一、匀变速直线运动的速度与时间的关系式
1.速度公式:vt=_____。
2.对速度公式的理解:
(1)速度公式中,末速度vt是时间t的一次函数,其v-t图线是一条倾斜的直线,斜
率表示加速度a,纵轴截距表示初速度v0。
(2)速度公式既适用于匀加速直线运动,也适用于匀减速直线运动。
(3)此公式中有四个物理量,知道其中三个就可以求第四个物理量。
v0+at
二、速度方程的深入讨论
一般情况下,以初速度v0的方向为正方向,即v0为正值。
(1)若a与v0同向,则a是_____。
(2)若a与v0反向,则a是_____。
(3)若a=0,物体匀速直线运动。
正值
负值
【易错辨析】
(1)匀变速直线运动的加速度不变。
(
)
(2)公式vt=v0+at适用于任何做直线运动的物体。
(
)
(3)匀加速直线运动的v-t图像的斜率逐渐增大。
(
)
(4)速度增大的运动是匀加速直线运动。
(
)
(5)速度减小的运动一定是匀减速直线运动。
(
)
(6)速度均匀增加(或减小)的运动是匀变速直线运动。
(
)
√
×
×
×
×
√
关键能力·合作学习
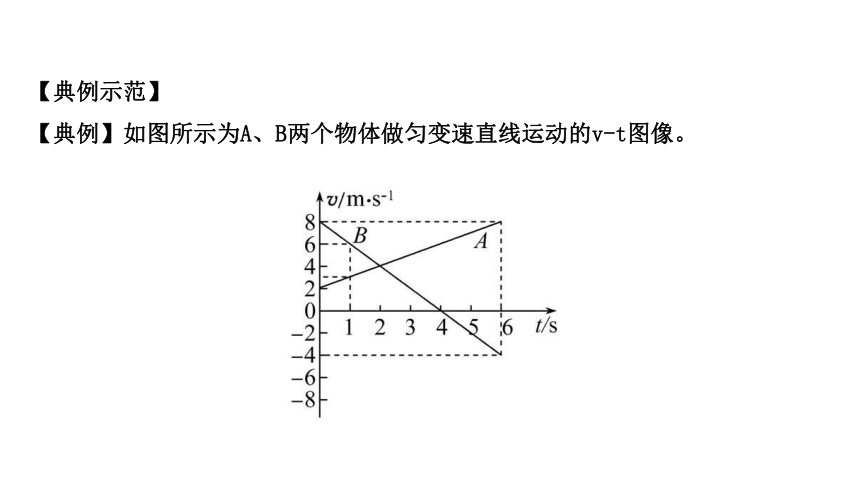
知识点一 匀变速直线运动的v-t图像
图线上某
点的纵坐标
正负号
表示瞬时速度的方向
绝对值
表示瞬时速度的大小
图线的斜率
正负号
表示加速度的方向
绝对值
表示加速度的大小
图线与坐标
轴的交点
纵截距
表示初速度
横截距
表示开始运动或速度为零的时刻
图线的拐点
表示加速度改变
两图线的交点
表示速度相等
图线与横轴所围图形的面积
表示位移,面积在横轴上方时位移为正值,在横轴下方时位移为负值
提醒:v-t图像只能表示直线运动,理解斜率的物理意义。
【问题探究】
2018年10月29日,我国针对运载火箭垂直回收项目进行了一次技术验证,只见
一枚火箭升空后,又稳稳地垂直落回目标地点,圆满完成了此次技术验证。
讨论:(1)假如火箭在点火升空时做匀加速直线运动,则其速度—时间图像具有什么特点?
提示:是一条过原点的倾斜直线。
(2)匀变速直线运动的v-t图像有何作用?
提示:匀变速直线运动的v-t图像能够直观地反映速度随时间均匀变化的规律。
【典例示范】
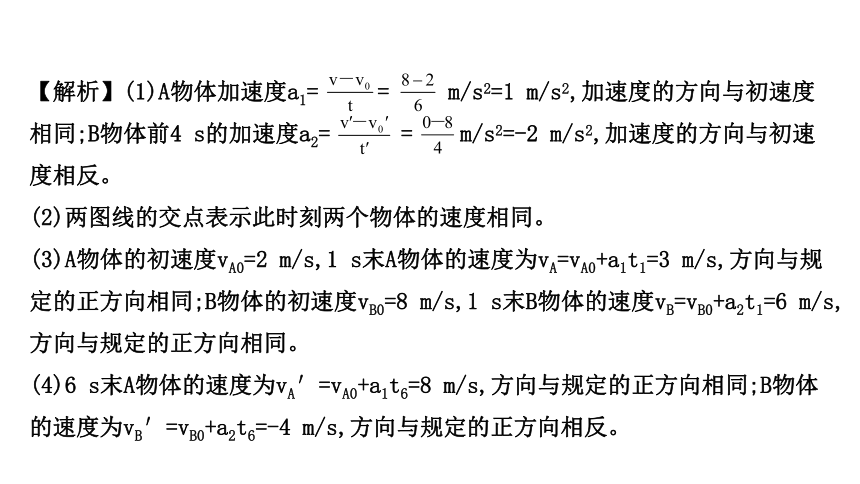
【典例】如图所示为A、B两个物体做匀变速直线运动的v-t图像。
(1)A、B两个物体各做什么运动?求其加速度;
(2)两图线的交点的意义是什么?
(3)求1
s末A、B两个物体的速度;
(4)求6
s末A、B两个物体的速度。
【解析】(1)A物体加速度a1=
=
m/s2=1
m/s2,加速度的方向与初速度
相同;B物体前4
s的加速度a2=
=
m/s2=-2
m/s2,加速度的方向与初速
度相反。
(2)两图线的交点表示此时刻两个物体的速度相同。
(3)A物体的初速度vA0=2
m/s,1
s末A物体的速度为vA=vA0+a1t1=3
m/s,方向与规
定的正方向相同;B物体的初速度vB0=8
m/s,1
s末B物体的速度vB=vB0+a2t1=6
m/s,
方向与规定的正方向相同。
(4)6
s末A物体的速度为vA′=vA0+a1t6=8
m/s,方向与规定的正方向相同;B物体
的速度为vB′=vB0+a2t6=-4
m/s,方向与规定的正方向相反。
【规律方法】由v-t图像可以直观判定的物理量
(1)速度变化:远离t轴为加速,靠近t轴为减速。
(2)加速度正负:图线斜向上为正,斜向下为负。
(3)加速度大小:
①图线为直线的,加速度恒定不变。
②图线为曲线的,斜率变大的加速度变大,斜率变小的加速度变小。
【素养训练】
1.如图所示是几个质点的运动图像,其中是匀变速直线运动的是
( )
A.甲、乙、丙 B.甲、乙、丁
C.甲、丙、丁
D.乙
【解析】选A。匀变速直线运动的v
-t图像为倾斜直线,a-t
图像为平行于t轴的直线,故所给图中甲、乙、丙表示物体做匀变速直线运动,而丁表示物体做变加速运动,故A项正确。
2.(多选)例题示范问题1中汽车
的匀变速运动过程,用图像描述,其中正确的是
( )
【解析】选A、C。汽车前5
s做匀加速直线运动,a与v同向,后2
s做匀减速直线运动,a与v反向,故A、C正确,B、D错误。
知识点二 匀变速直线运动公式的理解和应用
1.公式的适用条件:
公式vt=v0+at只适用于匀变速直线运动。
2.公式的矢量性:
(1)公式vt=v0+at中的v0、vt、a均为矢量,应用公式解题时,首先应选取正方向。
(2)一般以v0的方向为正方向,此时若为匀加速直线运动,则a>0,若为匀减速直线运动,则a<0;对于计算结果vt>0,说明vt与v0方向相同;vt<0,说明vt与v0方向相反。
加速度、初速度方向与运动性质的关系
3.两种特殊情况:
(1)当v0=0时,vt=at。
由于匀变速直线运动的加速度恒定不变,表明由静止开始的匀加速直线运动的速度大小与其运动时间成正比。
(2)当a=0时,vt=v0。
加速度为零的运动是匀速直线运动,也表明匀速直线运动是匀变速直线运动的特例。
4.中间时刻的瞬时速度推论:
物体做匀变速直线运动,A时刻速度为vA,B时刻速度为vB。则A、B的中间时刻的
瞬时速度为
=
。
【问题探究】2019年12月27日,C919大型客机106架机于10时15分从浦东机场第
四跑道起飞,经过2小时5分钟的飞行,在完成了30个试验点后,于12时20分返航
并平稳降落浦东机场,顺利完成其首次飞行任务。
(1)如果将C919大型客机在地面上滑行起飞的过程看作是匀加速直线运动,其运
动的速度与时间有什么关系?
提示:速度与时间的关系为:vt=v0+at。
(2)C919大型客机的起飞速度为315
km/h,滑行过程中的加速度为3
m/s2,其在跑道上滑行的时间与哪些物理量有关?
提示:加速度、起飞速度。
【典例示范】
【典例】火车正常行驶的速度是54
km/h,关闭发动机后,开始做匀减速直线运动,6
s末的速度是43.2
km/h,求:
(1)火车的加速度;
(2)15
s末的速度;
(3)45
s末的速度。
【解析】以火车运动的方向为正方向,
v0=54
km/h=15
m/s;v1=43.2
km/h=12
m/s
(1)由加速度定义式可知:
a=
=
m/s2=-0.5
m/s2
负号表示方向与火车运动方向相反;
(2)火车速度减为零的时间t=
=
s=30
s
所以15
s末的速度为:
v15=v0+at1=(15-0.5×15)
m/s=7.5
m/s;
(3)由(2)分析可知,火车从开始减速到停下所用时间为30
s,所以火车在45
s末
的速度为零。
答案:(1)0.5
m/s2,方向与火车运动方向相反
(2)7.5
m/s,方向与原速度方向一致 (3)0
【素养训练】
1.一辆汽车从静止开始启动,做匀加速直线运动,用了10
s的时间达到72
km/h的速度,然后以这个速度在平直公路上匀速行驶,突然司机发现前方公路上有一只小鹿,于是立即刹车,刹车过程中做匀减速直线运动,加速度大小为4
m/s2,求:
(1)汽车在启动加速时的加速度;
(2)开始刹车后2
s末的速度大小和6
s末的速度大小。
【解析】(1)选汽车的运动方向为正方向,
在启动过程,初速度v0=0,
末速度v1=72
km/h=20
m/s,加速时间t1=10
s,
所以启动时的加速度为
a1=
m/s2=2
m/s2。
即启动时的加速度大小为2
m/s2,方向与汽车的运动方向相同。
(2)汽车刹车过程的加速度为a2=-4
m/s2
设汽车停止所用时间为t0
由0=v1+a2t0,
得汽车停止所需要的时间为t0=5
s,
所以开始刹车后2
s末的速度为
v2=v1+a2t2=(20-4×2)
m/s=12
m/s,
由于6
s>5
s,所以开始刹车后6
s末的速度为0。
答案:(1)2
m/s2,方向与汽车的运动方向相同
(2)12
m/s 0
2.一辆公共汽车由静止出发做匀加速直线运动,加速度大小为2
m/s2,6
s后改做匀速直线运动,快到下一站时关闭发动机做匀减速直线运动,再经过12
s停止,求:
(1)汽车匀速行驶时的速度;
(2)汽车关闭发动机后的加速度;
(3)汽车在匀速行驶的过程中突遇紧急情况,需要停车,若其刹车的加速度大小为4
m/s2,那么刹车后2
s和5
s的速度各为多少?
【解析】(1)匀速运动的速度为匀加速直线运动的末速度,v1=a1t1=2×6
m/s=
12
m/s。
(2)关闭发动机后,汽车做初速度为v1、末速度为0的匀减速直线运动,则加速度
a2=
m/s2=-1
m/s2,负号表示汽车加速度方向与运动方向相反。
(3)中途紧急刹车,设汽车停止所需的时间为t0,则
t0=
s=3
s
t1′=2
s<3
s,则2
s时的速度
v2=v1+at1′=[12+(-4)×2]
m/s=4
m/s
t2′=5
s>3
s,此时汽车已停止,其速度v5=0
答案:(1)12
m/s (2)-1
m/s2,负号表示汽车加速度方向与运动方向相反
(3)4
m/s 0
【加固训练】
矿井里的升降机,从矿井底部由静止开始匀加速上升,经5
s速度达到8
m/s后,又以此速度匀速上升10
s,然后匀减速上升,又经10
s停在井口。求:
(1)加速和减速的加速度a1和a2的大小;
(2)匀速上升的高度。
【解析】从静止匀加速上升阶段
由速度公式v=v0+a1t1和v0=0得v=a1t1
a1=
m/s2=1.6
m/s2
以后以v=8
m/s匀速上升,上升高度
h=vt2=8×10
m=80
m
最后以v=8
m/s的初速度匀减速上升10
s停止,末速度v′=0
有v+a2t3=0得a2=
m/s2=-0.8
m/s2
减速上升的加速度大小为0.8
m/s2
答案:(1)1.6
m/s2 0.8
m/s2 (2)80
m
【拓展例题】考查内容:匀变速直线运动中的多解问题
【典例】如图所示,小球以6
m/s的速度由足够长的光滑斜面中部沿着斜面向上
滑。已知小球在斜面上运动的加速度大小为2
m/s2,则小球的速度大小何时达到
3
m/s?(小球在光滑斜面上运动时,加速度的大小、方向都不改变)
【解析】小球先沿斜面向上做匀减速直线运动,速度由6
m/s逐渐减小为零,然
后又反向做匀加速直线运动,取沿斜面向上的方向为正方向,则v0=6
m/s,a=
-2
m/s2,小球的速度大小为3
m/s,有两种情况:向上滑时v1=3
m/s,向下滑时v2
=-3
m/s。
由公式v=v0+at得t=
所以t1=
s=1.5
s
t2=
s=4.5
s
答案:1.5
s或4.5
s
公式:v=v0+at
特例
a=0时,v=v0
v0=0时,v=at
v
t
a、v同向:匀加速直线运动
a、v反向:匀减速直线运动
①
①
②
②
③
③
O
分类
匀变速直线运动
v-t图像
速度与时间公式
利用光电门测速度:
光电门是一种可以测量物体瞬时速度的器材,它利用的基本原理是:极短时间内
的平均速度大小可以近似认为是该时刻的瞬时速度大小。如图所示为用光电门
测速度的实验装置。
情境·模型·素养
探究:
如某次宽为d=1.5
cm的挡光片通过光电门,计时器上显示的时间是Δt=0.015
s,则挡光片通过光电门时的瞬时速度大小为多少?
【解析】v=
=1.0
m/s。
答案:1.0
m/s
某品牌汽车尾部标识有30TFSI、35TFSI、40TFSI等字样。前面数字叫G值,用来
表现车型的整体加速度感,数字越大,加速越快。G值的大小为车辆完成百公里
加速的平均加速度数值再乘10。如图为某品牌汽车尾部标有45TFSI字样。
探究:此汽车百公里加速时间是多少?
【解析】完成百公里加速的G值为
G=
×10,
解得t=6.2
s。
答案:6.2
s
课堂检测·素养达标
1.下列说法正确的是
( )
A.若物体的加速度均匀增加,则物体做匀加速直线运动
B.若物体的加速度均匀减小,则物体做匀减速直线运动
C.若物体加速度与其速度方向相反,则物体做减速直线运动
D.若物体在任意的相等时间间隔内位移相等,则物体做匀变速直线运动
【解析】选C。匀加速直线运动、匀减速直线运动的加速度保持不变,故A、B错误。若加速度方向与速度方向相反,则物体做减速直线运动,故C正确。物体在任意相等时间间隔内位移相等,则物体的速度保持不变,物体做匀速直线运动,故D错误。
2.(多选)物体运动的初速度为6
m/s,经过10
s速度的大小变为20
m/s,则加速度大小可能是
( )
A.0.8
m/s2
B.1.4
m/s2
C.2.0
m/s2
D.2.6
m/s2
【解析】选B、D。当10
s末的速度方向与初速度方向相同,则加速度a=
m/s2=1.4
m/s2,当10
s末的速度方向与初速度方向相反,则加速度
a=
m/s2=-2.6
m/s2,负号表示方向,故B、D正确,A、C错误。
3.如图所示为某质点的速度—时间图像,则下列说法中正确的是
( )
A.在0~6
s内,质点做匀变速直线运动
B.在t=12
s末,质点的加速度为-1
m/s2
C.在6~10
s内,质点处于静止状态
D.在4
s末,质点运动方向改变
【解析】选B。在0~6
s内,质点先做匀加速直线运动,后做匀减速直线运动,所
以做的是非匀变速直线运动,故A错误;在t=12
s末,质点的加速度为a=
m/s2=-1
m/s2,故B正确;在6~10
s内,质点做匀速直线运动,故C错误;在
14
s内,质点的速度都为正,一直沿正方向运动,运动方向没有改变,故D错误。
4.(多选)如图所示,一滑雪运动员从一段长的山坡上匀加速滑下,初速度是
1.8
m/s,末速度是5.0
m/s,用时25
s,关于滑雪运动员,下列说法正确的
是( )
A.通过这段斜坡的加速度为0.128
m/s2
B.通过这段斜坡的加速度为1.28
m/s2
C.通过斜坡中间时刻的速度为3.4
m/s
D.能过斜坡中间时刻的速度为1.6
m/s
【解析】选A、C。由vt=v0+at得a=0.128
m/s2,A对,B错;由
得
=3.4
m/s,C对,D错。
5.汽车的加速、减速性能是衡量汽车性能的重要指标,一辆汽车以54
km/h的速度匀速行驶。
(1)若汽车以1.5
m/s2的加速度加速,求8
s后汽车的速度大小。
(2)若汽车以1.5
m/s2的加速度刹车,分别求刹车8
s时和12
s时的速度大小。
初速度v0=54
km/h=15
m/s。
(1)由v=v0+at,得8
s后的速度v=(15+1.5×8)
m/s=27
m/s。
(2)刹车过程中汽车做匀减速运动,a′=-1.5
m/s2
减速到停止所用时间t′=
s=10
s
所以刹车8
s时的速度v′=v0+a′t=(15-1.5×8)
m/s=3
m/s
刹车12
s时的速度为零。
答案:(1)27
m/s (2)3
m/s 0
2.匀变速直线运动速度与时间的关系
必备知识·自主学习
一、匀变速直线运动的速度与时间的关系式
1.速度公式:vt=_____。
2.对速度公式的理解:
(1)速度公式中,末速度vt是时间t的一次函数,其v-t图线是一条倾斜的直线,斜
率表示加速度a,纵轴截距表示初速度v0。
(2)速度公式既适用于匀加速直线运动,也适用于匀减速直线运动。
(3)此公式中有四个物理量,知道其中三个就可以求第四个物理量。
v0+at
二、速度方程的深入讨论
一般情况下,以初速度v0的方向为正方向,即v0为正值。
(1)若a与v0同向,则a是_____。
(2)若a与v0反向,则a是_____。
(3)若a=0,物体匀速直线运动。
正值
负值
【易错辨析】
(1)匀变速直线运动的加速度不变。
(
)
(2)公式vt=v0+at适用于任何做直线运动的物体。
(
)
(3)匀加速直线运动的v-t图像的斜率逐渐增大。
(
)
(4)速度增大的运动是匀加速直线运动。
(
)
(5)速度减小的运动一定是匀减速直线运动。
(
)
(6)速度均匀增加(或减小)的运动是匀变速直线运动。
(
)
√
×
×
×
×
√
关键能力·合作学习
知识点一 匀变速直线运动的v-t图像
图线上某
点的纵坐标
正负号
表示瞬时速度的方向
绝对值
表示瞬时速度的大小
图线的斜率
正负号
表示加速度的方向
绝对值
表示加速度的大小
图线与坐标
轴的交点
纵截距
表示初速度
横截距
表示开始运动或速度为零的时刻
图线的拐点
表示加速度改变
两图线的交点
表示速度相等
图线与横轴所围图形的面积
表示位移,面积在横轴上方时位移为正值,在横轴下方时位移为负值
提醒:v-t图像只能表示直线运动,理解斜率的物理意义。
【问题探究】
2018年10月29日,我国针对运载火箭垂直回收项目进行了一次技术验证,只见
一枚火箭升空后,又稳稳地垂直落回目标地点,圆满完成了此次技术验证。
讨论:(1)假如火箭在点火升空时做匀加速直线运动,则其速度—时间图像具有什么特点?
提示:是一条过原点的倾斜直线。
(2)匀变速直线运动的v-t图像有何作用?
提示:匀变速直线运动的v-t图像能够直观地反映速度随时间均匀变化的规律。
【典例示范】
【典例】如图所示为A、B两个物体做匀变速直线运动的v-t图像。
(1)A、B两个物体各做什么运动?求其加速度;
(2)两图线的交点的意义是什么?
(3)求1
s末A、B两个物体的速度;
(4)求6
s末A、B两个物体的速度。
【解析】(1)A物体加速度a1=
=
m/s2=1
m/s2,加速度的方向与初速度
相同;B物体前4
s的加速度a2=
=
m/s2=-2
m/s2,加速度的方向与初速
度相反。
(2)两图线的交点表示此时刻两个物体的速度相同。
(3)A物体的初速度vA0=2
m/s,1
s末A物体的速度为vA=vA0+a1t1=3
m/s,方向与规
定的正方向相同;B物体的初速度vB0=8
m/s,1
s末B物体的速度vB=vB0+a2t1=6
m/s,
方向与规定的正方向相同。
(4)6
s末A物体的速度为vA′=vA0+a1t6=8
m/s,方向与规定的正方向相同;B物体
的速度为vB′=vB0+a2t6=-4
m/s,方向与规定的正方向相反。
【规律方法】由v-t图像可以直观判定的物理量
(1)速度变化:远离t轴为加速,靠近t轴为减速。
(2)加速度正负:图线斜向上为正,斜向下为负。
(3)加速度大小:
①图线为直线的,加速度恒定不变。
②图线为曲线的,斜率变大的加速度变大,斜率变小的加速度变小。
【素养训练】
1.如图所示是几个质点的运动图像,其中是匀变速直线运动的是
( )
A.甲、乙、丙 B.甲、乙、丁
C.甲、丙、丁
D.乙
【解析】选A。匀变速直线运动的v
-t图像为倾斜直线,a-t
图像为平行于t轴的直线,故所给图中甲、乙、丙表示物体做匀变速直线运动,而丁表示物体做变加速运动,故A项正确。
2.(多选)例题示范问题1中汽车
的匀变速运动过程,用图像描述,其中正确的是
( )
【解析】选A、C。汽车前5
s做匀加速直线运动,a与v同向,后2
s做匀减速直线运动,a与v反向,故A、C正确,B、D错误。
知识点二 匀变速直线运动公式的理解和应用
1.公式的适用条件:
公式vt=v0+at只适用于匀变速直线运动。
2.公式的矢量性:
(1)公式vt=v0+at中的v0、vt、a均为矢量,应用公式解题时,首先应选取正方向。
(2)一般以v0的方向为正方向,此时若为匀加速直线运动,则a>0,若为匀减速直线运动,则a<0;对于计算结果vt>0,说明vt与v0方向相同;vt<0,说明vt与v0方向相反。
加速度、初速度方向与运动性质的关系
3.两种特殊情况:
(1)当v0=0时,vt=at。
由于匀变速直线运动的加速度恒定不变,表明由静止开始的匀加速直线运动的速度大小与其运动时间成正比。
(2)当a=0时,vt=v0。
加速度为零的运动是匀速直线运动,也表明匀速直线运动是匀变速直线运动的特例。
4.中间时刻的瞬时速度推论:
物体做匀变速直线运动,A时刻速度为vA,B时刻速度为vB。则A、B的中间时刻的
瞬时速度为
=
。
【问题探究】2019年12月27日,C919大型客机106架机于10时15分从浦东机场第
四跑道起飞,经过2小时5分钟的飞行,在完成了30个试验点后,于12时20分返航
并平稳降落浦东机场,顺利完成其首次飞行任务。
(1)如果将C919大型客机在地面上滑行起飞的过程看作是匀加速直线运动,其运
动的速度与时间有什么关系?
提示:速度与时间的关系为:vt=v0+at。
(2)C919大型客机的起飞速度为315
km/h,滑行过程中的加速度为3
m/s2,其在跑道上滑行的时间与哪些物理量有关?
提示:加速度、起飞速度。
【典例示范】
【典例】火车正常行驶的速度是54
km/h,关闭发动机后,开始做匀减速直线运动,6
s末的速度是43.2
km/h,求:
(1)火车的加速度;
(2)15
s末的速度;
(3)45
s末的速度。
【解析】以火车运动的方向为正方向,
v0=54
km/h=15
m/s;v1=43.2
km/h=12
m/s
(1)由加速度定义式可知:
a=
=
m/s2=-0.5
m/s2
负号表示方向与火车运动方向相反;
(2)火车速度减为零的时间t=
=
s=30
s
所以15
s末的速度为:
v15=v0+at1=(15-0.5×15)
m/s=7.5
m/s;
(3)由(2)分析可知,火车从开始减速到停下所用时间为30
s,所以火车在45
s末
的速度为零。
答案:(1)0.5
m/s2,方向与火车运动方向相反
(2)7.5
m/s,方向与原速度方向一致 (3)0
【素养训练】
1.一辆汽车从静止开始启动,做匀加速直线运动,用了10
s的时间达到72
km/h的速度,然后以这个速度在平直公路上匀速行驶,突然司机发现前方公路上有一只小鹿,于是立即刹车,刹车过程中做匀减速直线运动,加速度大小为4
m/s2,求:
(1)汽车在启动加速时的加速度;
(2)开始刹车后2
s末的速度大小和6
s末的速度大小。
【解析】(1)选汽车的运动方向为正方向,
在启动过程,初速度v0=0,
末速度v1=72
km/h=20
m/s,加速时间t1=10
s,
所以启动时的加速度为
a1=
m/s2=2
m/s2。
即启动时的加速度大小为2
m/s2,方向与汽车的运动方向相同。
(2)汽车刹车过程的加速度为a2=-4
m/s2
设汽车停止所用时间为t0
由0=v1+a2t0,
得汽车停止所需要的时间为t0=5
s,
所以开始刹车后2
s末的速度为
v2=v1+a2t2=(20-4×2)
m/s=12
m/s,
由于6
s>5
s,所以开始刹车后6
s末的速度为0。
答案:(1)2
m/s2,方向与汽车的运动方向相同
(2)12
m/s 0
2.一辆公共汽车由静止出发做匀加速直线运动,加速度大小为2
m/s2,6
s后改做匀速直线运动,快到下一站时关闭发动机做匀减速直线运动,再经过12
s停止,求:
(1)汽车匀速行驶时的速度;
(2)汽车关闭发动机后的加速度;
(3)汽车在匀速行驶的过程中突遇紧急情况,需要停车,若其刹车的加速度大小为4
m/s2,那么刹车后2
s和5
s的速度各为多少?
【解析】(1)匀速运动的速度为匀加速直线运动的末速度,v1=a1t1=2×6
m/s=
12
m/s。
(2)关闭发动机后,汽车做初速度为v1、末速度为0的匀减速直线运动,则加速度
a2=
m/s2=-1
m/s2,负号表示汽车加速度方向与运动方向相反。
(3)中途紧急刹车,设汽车停止所需的时间为t0,则
t0=
s=3
s
t1′=2
s<3
s,则2
s时的速度
v2=v1+at1′=[12+(-4)×2]
m/s=4
m/s
t2′=5
s>3
s,此时汽车已停止,其速度v5=0
答案:(1)12
m/s (2)-1
m/s2,负号表示汽车加速度方向与运动方向相反
(3)4
m/s 0
【加固训练】
矿井里的升降机,从矿井底部由静止开始匀加速上升,经5
s速度达到8
m/s后,又以此速度匀速上升10
s,然后匀减速上升,又经10
s停在井口。求:
(1)加速和减速的加速度a1和a2的大小;
(2)匀速上升的高度。
【解析】从静止匀加速上升阶段
由速度公式v=v0+a1t1和v0=0得v=a1t1
a1=
m/s2=1.6
m/s2
以后以v=8
m/s匀速上升,上升高度
h=vt2=8×10
m=80
m
最后以v=8
m/s的初速度匀减速上升10
s停止,末速度v′=0
有v+a2t3=0得a2=
m/s2=-0.8
m/s2
减速上升的加速度大小为0.8
m/s2
答案:(1)1.6
m/s2 0.8
m/s2 (2)80
m
【拓展例题】考查内容:匀变速直线运动中的多解问题
【典例】如图所示,小球以6
m/s的速度由足够长的光滑斜面中部沿着斜面向上
滑。已知小球在斜面上运动的加速度大小为2
m/s2,则小球的速度大小何时达到
3
m/s?(小球在光滑斜面上运动时,加速度的大小、方向都不改变)
【解析】小球先沿斜面向上做匀减速直线运动,速度由6
m/s逐渐减小为零,然
后又反向做匀加速直线运动,取沿斜面向上的方向为正方向,则v0=6
m/s,a=
-2
m/s2,小球的速度大小为3
m/s,有两种情况:向上滑时v1=3
m/s,向下滑时v2
=-3
m/s。
由公式v=v0+at得t=
所以t1=
s=1.5
s
t2=
s=4.5
s
答案:1.5
s或4.5
s
公式:v=v0+at
特例
a=0时,v=v0
v0=0时,v=at
v
t
a、v同向:匀加速直线运动
a、v反向:匀减速直线运动
①
①
②
②
③
③
O
分类
匀变速直线运动
v-t图像
速度与时间公式
利用光电门测速度:
光电门是一种可以测量物体瞬时速度的器材,它利用的基本原理是:极短时间内
的平均速度大小可以近似认为是该时刻的瞬时速度大小。如图所示为用光电门
测速度的实验装置。
情境·模型·素养
探究:
如某次宽为d=1.5
cm的挡光片通过光电门,计时器上显示的时间是Δt=0.015
s,则挡光片通过光电门时的瞬时速度大小为多少?
【解析】v=
=1.0
m/s。
答案:1.0
m/s
某品牌汽车尾部标识有30TFSI、35TFSI、40TFSI等字样。前面数字叫G值,用来
表现车型的整体加速度感,数字越大,加速越快。G值的大小为车辆完成百公里
加速的平均加速度数值再乘10。如图为某品牌汽车尾部标有45TFSI字样。
探究:此汽车百公里加速时间是多少?
【解析】完成百公里加速的G值为
G=
×10,
解得t=6.2
s。
答案:6.2
s
课堂检测·素养达标
1.下列说法正确的是
( )
A.若物体的加速度均匀增加,则物体做匀加速直线运动
B.若物体的加速度均匀减小,则物体做匀减速直线运动
C.若物体加速度与其速度方向相反,则物体做减速直线运动
D.若物体在任意的相等时间间隔内位移相等,则物体做匀变速直线运动
【解析】选C。匀加速直线运动、匀减速直线运动的加速度保持不变,故A、B错误。若加速度方向与速度方向相反,则物体做减速直线运动,故C正确。物体在任意相等时间间隔内位移相等,则物体的速度保持不变,物体做匀速直线运动,故D错误。
2.(多选)物体运动的初速度为6
m/s,经过10
s速度的大小变为20
m/s,则加速度大小可能是
( )
A.0.8
m/s2
B.1.4
m/s2
C.2.0
m/s2
D.2.6
m/s2
【解析】选B、D。当10
s末的速度方向与初速度方向相同,则加速度a=
m/s2=1.4
m/s2,当10
s末的速度方向与初速度方向相反,则加速度
a=
m/s2=-2.6
m/s2,负号表示方向,故B、D正确,A、C错误。
3.如图所示为某质点的速度—时间图像,则下列说法中正确的是
( )
A.在0~6
s内,质点做匀变速直线运动
B.在t=12
s末,质点的加速度为-1
m/s2
C.在6~10
s内,质点处于静止状态
D.在4
s末,质点运动方向改变
【解析】选B。在0~6
s内,质点先做匀加速直线运动,后做匀减速直线运动,所
以做的是非匀变速直线运动,故A错误;在t=12
s末,质点的加速度为a=
m/s2=-1
m/s2,故B正确;在6~10
s内,质点做匀速直线运动,故C错误;在
14
s内,质点的速度都为正,一直沿正方向运动,运动方向没有改变,故D错误。
4.(多选)如图所示,一滑雪运动员从一段长的山坡上匀加速滑下,初速度是
1.8
m/s,末速度是5.0
m/s,用时25
s,关于滑雪运动员,下列说法正确的
是( )
A.通过这段斜坡的加速度为0.128
m/s2
B.通过这段斜坡的加速度为1.28
m/s2
C.通过斜坡中间时刻的速度为3.4
m/s
D.能过斜坡中间时刻的速度为1.6
m/s
【解析】选A、C。由vt=v0+at得a=0.128
m/s2,A对,B错;由
得
=3.4
m/s,C对,D错。
5.汽车的加速、减速性能是衡量汽车性能的重要指标,一辆汽车以54
km/h的速度匀速行驶。
(1)若汽车以1.5
m/s2的加速度加速,求8
s后汽车的速度大小。
(2)若汽车以1.5
m/s2的加速度刹车,分别求刹车8
s时和12
s时的速度大小。
初速度v0=54
km/h=15
m/s。
(1)由v=v0+at,得8
s后的速度v=(15+1.5×8)
m/s=27
m/s。
(2)刹车过程中汽车做匀减速运动,a′=-1.5
m/s2
减速到停止所用时间t′=
s=10
s
所以刹车8
s时的速度v′=v0+a′t=(15-1.5×8)
m/s=3
m/s
刹车12
s时的速度为零。
答案:(1)27
m/s (2)3
m/s 0
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
