2021-2022学年教科版(2019)必修第一册 2.4匀变速直线运动规律的应用 课件(42张PPT)
文档属性
| 名称 | 2021-2022学年教科版(2019)必修第一册 2.4匀变速直线运动规律的应用 课件(42张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-20 00:00:00 | ||
图片预览











文档简介
(共42张PPT)
4.匀变速直线运动规律的应用
必备知识·自主学习
【情境思考】
如图,A、B、C三个标志牌间距相等为x,汽车做匀加速直线运动,加速度为a,
已知汽车经过标志牌A的速度为vA,你能求出汽车经过标志牌B和C的速度vB和vC
吗?
提示:由
=2ax,解得vB=
;
由
=2a·2x,解得vC=
1.位移与速度的关系式:
=2ax,若v0=0,则关系式为
。
2.公式推导:速度公式vt=_____,
①
位移公式x=
__________,
②
由①②式解得
=2ax。
3.位移与速度关系式是矢量式,使用时应先规定正方向,以便确定v0、vt、a、x
的正负。
v0+at
v0t+
at2
4.以下对匀变速直线运动规律的应用,符合科学实际的有_____。
①公式
=2ax中
前面的“-”号表示运算符号,不代表方向;
②加速度公式a=
和a=
既适用于匀变速直线运动,又适用于非匀变
速直线运动;
③计算位移的关系式x=v0t+
at2、x=
t和x=
都是只适用于匀变
速直线运动。
①③
【易错辨析】
(1)公式
适用于任何直线运动。
(
)
(2)物体的末速度越大,位移越大。
(
)
(3)对匀减速直线运动,公式
中的a必须取负值。
(
)
(4)公式
中的x有时和路程相等。
(
)
×
×
×
√
关键能力·合作学习
知识点一 速度—位移公式的分析和应用
1.公式的适用条件:公式表述的是匀变速直线运动的速度与位移的关系,适用于
匀变速直线运动。
2.公式的意义:公式2ax=
反映了初速度v0、末速度vt、加速度a、位移x
之间的关系,当其中三个物理量已知时,可求另一个未知量。
3.公式的矢量性:公式中v0、vt、a、x都是矢量,应用时必须选取统一的正方向,
一般选v0方向为正方向。
(1)物体做加速运动时,a取正值,做减速运动时,a取负值。
(2)x>0,说明物体通过的位移方向与初速度方向相同;x<0,说明位移的方向与初
速度的方向相反。
4.两种特殊形式:
(1)当v0=0时,
=2ax(初速度为零的匀加速直线运动)。
(2)当vt=0时,-
=2ax(末速度为零的匀减速直线运动)。
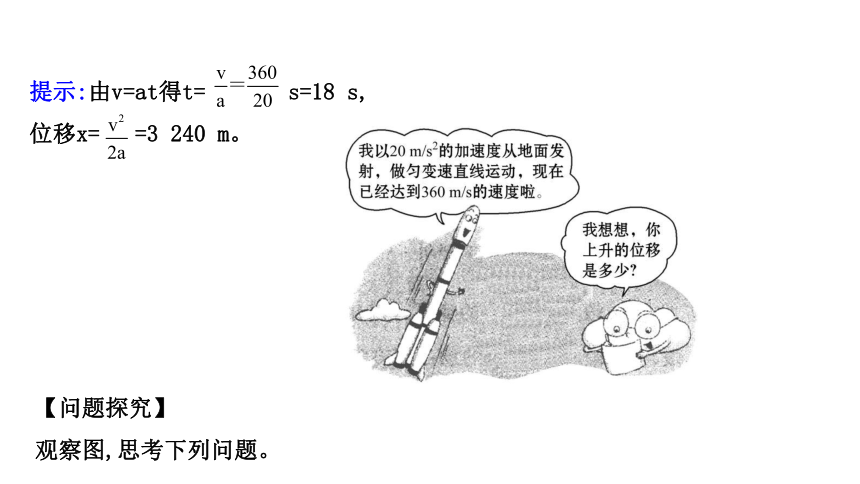
【问题探究】
观察图,思考下列问题。
提示:由v=at得t=
s=18
s,
位移x=
=3
240
m。
【典例示范】
【典例】随着机动车数量的增加,交通安全问题日益凸显。分析交通违法事例,将警示我们遵守交通法规,珍惜生命。一货车严重超载后的总质量为49
t,以
54
km/h的速率匀速行驶。发现红灯时司机刹车,货车立即做匀减速直线运动,加速度的大小为2.5
m/s2(不超载时则为5
m/s2)。
(1)若前方无阻挡,问从刹车到停下来此货车在超载及不超载时分别前进多远?
(2)若超载货车刹车时正前方25
m处停着总质量为1
t的轿车,两车将发生碰撞,求相撞时货车的速度。
【解析】(1)设货车刹车时速度大小为v0,加速度大小为a,末速度大小为v,刹车
距离为x,根据匀变速直线运动的速度与位移的关系式得x=
由题意知,v0=54
km/h=15
m/s,v=0,a1=2.5
m/s2,a2=5
m/s2
代入数据得,超载时x1=45
m
不超载时x2=22.5
m
(2)超载货车与轿车碰撞时,由
=-2ax知
相撞时货车的速度
vt=
m/s=10
m/s
答案:(1)45
m 22.5
m (2)10
m/s
【素养训练】
1.(2020·泰安高一检测)做匀加速直线运动的物体,速度从v增加到3v时经过的
位移是x,则它的速度从3v增加到5v时经过的位移是
( )
A.
x
B.
x
C.
x
D.2x
【解析】选D。根据速度—位移公式得(3v)2-v2=2ax,(5v)2-(3v)2=2ax′,联立两式解得x′=2x,故选项D正确。
2.一物体从静止开始以a1=6
m/s2做匀加速直线运动,通过的距离为x1,所用时间
为t1,达到某一速度后立即开始做匀减速直线运动直至速度为零,减速阶段的加
速度大小为a2=8
m/s2,通过的距离为x2,所用时间为t2。则下列说法正确的是
( )
A.x1∶x2=3∶
4,t1∶t2=3∶4
B.
x1∶x2=3∶4,t1∶t2=4∶3
C.x1∶x2=4∶3,t1∶t2=3∶4
D.x1∶x2=4∶3,t1∶t2=4∶3
【解析】选D。由题意得:x1=
,x2=
,则两式相比得到:
,由
v=at得
,故D正确,A、B、C错误;故选D。
知识点二 六个比例式
初速度为零的匀加速直线运动的常用推论
(1)等分运动时间(以T为时间单位)。
①1T末、2T末、3T末…瞬时速度之比:
由v=at可得:v1∶v2∶v3…=1∶2∶3…
②1T内、2T内、3T内…位移之比:
由x=
at2可得:x1∶x2∶x3…=1∶4∶9…
③第一个T内、第二个T内、第三个T内…的位移之比:
由xⅠ=x1,xⅡ=x2-x1,xⅢ=x3-x2…可得:
xⅠ∶xⅡ∶xⅢ…=1∶3∶5…
(2)等分位移(以x为单位)。
①通过x、2x、3x…所用时间之比:
由x=
at2可得t=
,所以
t1∶t2∶t3…=1∶
∶
…
②通过第一个x、第二个x、第三个x…所用时间之比:
由tⅠ=t1,tⅡ=t2-t1,tⅢ=t3-t2…可得:
tⅠ∶tⅡ∶tⅢ…=1∶(
-1)∶(
-
)…
③x末、2x末、3x末…的瞬时速度之比:
由v2=2ax可得v=
,所以
v1∶v2∶v3…=1∶
∶
…
【典例示范】
【典例】(多选)(2020·南通高一检测)一观察者站在第一节车厢前端,当列车
从静止开始做匀加速运动时(设每节车厢的长度相同,车厢间间隙可以不计)
( )
A.每节车厢末端经过观察者的速度之比是1∶
∶
∶…∶
B.每节车厢末端经过观察者的速度之比是1∶2∶3∶…∶n
C.在相等时间里经过观察者的车厢数之比是1∶3∶5∶…
D.在相等时间里经过观察者的车厢数之比是1∶2∶3∶…
【解析】选A、C。设每节车厢长为l,由v2=2ax得第一节车厢末端经过观察者时
v1=
,同理,第二节车厢末端经过观察者时v2=
……第n节车厢末端经
过观察者时,vn=
,所以有v1∶v2∶v3∶…∶vn=1∶
∶
∶…∶
,选
项A正确;相等时间里经过观察者的车厢数之比是1∶3∶5∶…,选项C正确。
【规律方法】处理直线运动的方法口诀
运用一般公式法,平均速度是简法。
中间时刻速度法,初速度为零比例法。
若是相邻等时间,位移逐差是妙法。
再加几何图像法,求解运动好方法。
【素养训练】一个物体从静止开始做匀加速直线运动,它在第1
s内与第2
s内
的位移之比为x1∶x2,在走完第1
m时与走完第2
m时的速度之比为v1∶v2。以下
说法正确的是
( )
A.x1∶x2=1∶3,v1∶v2=1∶2
B.x1∶x2=1∶3,v1∶v2=1∶
C.x1∶x2=1∶4,v1∶v2=1∶2
D.x1∶x2=1∶4,v1∶v2=1∶
【解析】选B。由初速度为零的匀变速直线运动的比例关系知x1∶x2=1∶3,由x=
at2知,走完1
m与走完2
m所用时间之比为t1∶t2=1∶
,又v=at,可得
v1∶v2=1∶
,选项B正确。
【加固训练】
飞机、火车、汽车等交通工具由静止到稳定运动的过程都可以看作初速度为零的匀加速直线运动。若一辆汽车从静止开始做匀加速直线运动,则求汽车:
(1)1
s末、2
s末、3
s末瞬时速度之比。
(2)1
s内、2
s内、3
s内的位移之比。
(3)第1
s内、第2
s内、第3
s内的位移之比。
(4)经过连续相等的位移,如经过第一个x、第二个x、第三个x所用时间之比。
【解析】(1)由v=at知:v1∶v2∶v3=1∶2∶3;
(2)由x=
at2得:x1∶x2∶x3=1∶22∶32=1∶4∶9;
(3)第1
s内位移xⅠ=
a×12
第2
s内位移xⅡ=
a×22-
a×12=
a×3
第3
s内位移为xⅢ=
a×32-
a×22=
a×5
故xⅠ∶xⅡ∶xⅢ=1∶3∶5;
(4)由x=
a
得第一个x所用时间tⅠ=
。
前2x所用时间t2=
故第二个x所用时间为
tⅡ=t2-tⅠ=(
-1)
同理第三个x所用时间tⅢ=(
-
)
所以有tⅠ∶tⅡ∶tⅢ=1∶(
-1)∶(
-
)。
答案:(1)1∶2∶3 (2)1∶4∶9 (3)1∶3∶5
(4)1∶(
-1)∶(
-
)
【拓展例题】考查内容:运动学公式的选择
【典例】如图所示,在成都天府大道某处安装了一台500万像素的固定雷达测速仪,可以准确抓拍超速车辆以及测量运动车辆的加速度。一辆汽车正从A点迎面驶向测速仪B,若测速仪与汽车相距355
m,此时测速仪发出超声波,同时车由于紧急情况而急刹车,汽车运动到C处与超声波相遇,当测速仪接收到反射回来的超声波信号时,汽车恰好停止于D点,且此时汽车与测速仪相距335
m,忽略测速仪安装高度的影响,可简化为如图所示分析(已知超声波速度为340
m/s)。
(1)求汽车刹车过程中的加速度a的大小。
(2)此路段有80
km/h的限速标志,分析该汽车刹车前的行驶速度是否超速。
【解析】(1)设超声波往返的时间为2t,汽车在2t时间内,刹车的位移为s=
a(2t)2=20
m,
当超声波与车相遇后,车继续前进的时间为t,位移为s2=
at2=5m,则超声波在2t内的路程为2×(335+5)
m=680
m,由声速为340
m/s,得
t=1
s,解得汽车的加速度a=10
m/s2
(2)车刹车过程中的位移s=
,
解得刹车前的速度v0=20
m/s=72
km/h
车速在规定范围内,不超速。
答案:(1)10
m/s2 (2)见解析
【生活情境】
冰壶(Curling),又称掷冰壶、冰上溜石,是以队为单位在冰上进行的一种投掷
性竞赛项目,冬奥会比赛项目,并设有冰壶世锦赛。冰壶周长约为91.44厘米,高
(从壶的底部到顶部)11.43厘米,重量(包括壶柄和壶栓)最大为19.96千克。刷
冰是为了减小冰壶与冰面间摩擦。
情境·模型·素养
探究:如图所示,一冰壶以速度v垂直进入两个相同的矩形区域做匀减速运动,且
刚要离开第二个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的
速度之比和穿过每个矩形区域所用的时间之比分别是多少?(冰壶可看成质点)
【解析】把冰壶的运动看成逆向的初速度为零的匀加速直线运动。冰壶通过两
矩形区域位移相等,则从右向左穿过矩形区域的速度之比为1∶
,则冰壶实际
运动依次进入每个矩形区域的速度之比为v1∶v2=
∶1;冰壶从右向左,通过每
个矩形区域的时间之比为1∶(
-1),则冰壶实际运动穿过区域的时间之比为
t1∶t2=(
-1)∶1。
答案:
∶1 (
-1)∶1
【生活情境】
冬天雾霾活动频繁,空气能见度降低,汽车沿平直公
路匀速行驶,遇到紧急情况
刹车,为避免发生事故,速度不宜过快。
探究:(1)若刹车加速度a恒定,刹车距离x跟速度v有
什么关系?
(2)某汽车在高速公路上行驶,若速度从70
km/h提速到100
km/h,问刹车距离变
成原来的多少倍?
【解析】(1)刹车距离跟速度的关系x=
。
(2)根据上式得,刹车距离变成原来的
倍。
答案:(1)x=
(2)
倍
课堂检测·素养达标
1.F1是英文Formula
One的缩写,即一级方程式赛车,是仅次于奥运会和世界杯的世界第三大赛事,假设赛车起动时加速度为5
m/s2,最大速度可达216
km/h,加速过程可以近似为匀加速直线运动,则赛车加速阶段的位移的大小是
( )
A.360
m
B.36
m
C.720
m
D.72
m
【解析】选A。由题意加速度a=5
m/s2,初速度v0=0,末速度v=216
km/h=
60
m/s。由x=
m=360
m,A正确。
2.一个物体沿着斜面从静止滑下做匀变速直线运动。已知它前2
s内的位移为
3
m,则它在第四个2
s内的位移是
( )
A.14
m B.21
m
C.24
m
D.48
m
【解析】选B。前2
s内的位移x1与第四个2
s内的位移x2之比x1∶x2=1∶(2×4-1)=1∶7,因为x1=3
m,所以x2=21
m,故B正确。
3.从静止开始做匀加速直线运动的物体,在第1
s内、第2
s内、第3
s内的平均
速度之比为
( )
A.1∶3∶5
B.1∶4∶9
C.1∶2∶3
D.1∶
∶
【解析】选A。由于第1
s内、第2
s内、第3
s内的位移之比x1∶x2∶x3
=1∶3∶5,而平均速度v=
,三段时间都是1
s,故三段时间的平均速
度之比为1∶3∶5,则A正确,B、C、D错误。
4.(多选)(教材二次开发·教材P46自我评价T1拓展变式)某汽车沿一直线运动,
在t时间内通过的位移为L,在
处速度为v1,在
处速度为v2,则
( )
A.匀加速运动,v1>v2
B.匀加速运动,v1C.匀减速运动,v1D.匀减速运动,v1>v2
【解析】选A、D。设汽车的初速度为v0,末速度为v,则在中间时刻时速度
v2=
,根据位移与时间公式可得
解得在中间位置时
的速度为v1=
,根据数学知识可得
>0,即无论汽车做匀加速运动还是匀减速运动,都有v1>v2,A、D正确。
本题也可以通过v-t图像解决问题,如图所示
5.舰载机在航母跑道上从静止开始做匀加速直线运动,以5
m/s2
的加速度运动,
需要达到50
m/s
的速度才可升空,如图所示。求:
(1)滑行5
s后,舰载机的速度大小?
(2)从启动到起飞,至少滑行多长时间?
(3)航母跑道至少多长?
【解析】(1)由匀变速直线运动规律得v=at=25
m/s;
(2)由匀变速直线运动规律得vm=at1,t1=10
s;
(3)由匀变速直线运动规律得
x=
m=250
m。
答案:(1)25
m/s (2)10
s (3)250
m
【加固训练】
一列火车进站前先关闭气阀,让车减速滑行,滑行了300
m
时速度减为关闭气阀时的一半,此后又继续滑行了20
s停在车站。设火车在滑行过程中加速度始终维持不变,试求:
(1)火车滑行的加速度大小。
(2)火车关闭气阀时的速度大小。
(3)从火车关闭气阀到停止滑行时,滑行的总位移。
【解析】设火车的加速度为a,初速度为v0,由位移与速度关系式得:(
)2-
=2ax1
①
由速度公式得:
0=
+at2
②
代入数据解①②得v0=20
m/s
a=-0.5
m/s2
由速度与位移的关系式得:2ax2=(
)2
代入数据解得x2=100
m
所以总位移
x=x1+x2=300
m+100
m=400
m
答案:(1)0.5
m/s2 (2)20
m/s (3)400
m
4.匀变速直线运动规律的应用
必备知识·自主学习
【情境思考】
如图,A、B、C三个标志牌间距相等为x,汽车做匀加速直线运动,加速度为a,
已知汽车经过标志牌A的速度为vA,你能求出汽车经过标志牌B和C的速度vB和vC
吗?
提示:由
=2ax,解得vB=
;
由
=2a·2x,解得vC=
1.位移与速度的关系式:
=2ax,若v0=0,则关系式为
。
2.公式推导:速度公式vt=_____,
①
位移公式x=
__________,
②
由①②式解得
=2ax。
3.位移与速度关系式是矢量式,使用时应先规定正方向,以便确定v0、vt、a、x
的正负。
v0+at
v0t+
at2
4.以下对匀变速直线运动规律的应用,符合科学实际的有_____。
①公式
=2ax中
前面的“-”号表示运算符号,不代表方向;
②加速度公式a=
和a=
既适用于匀变速直线运动,又适用于非匀变
速直线运动;
③计算位移的关系式x=v0t+
at2、x=
t和x=
都是只适用于匀变
速直线运动。
①③
【易错辨析】
(1)公式
适用于任何直线运动。
(
)
(2)物体的末速度越大,位移越大。
(
)
(3)对匀减速直线运动,公式
中的a必须取负值。
(
)
(4)公式
中的x有时和路程相等。
(
)
×
×
×
√
关键能力·合作学习
知识点一 速度—位移公式的分析和应用
1.公式的适用条件:公式表述的是匀变速直线运动的速度与位移的关系,适用于
匀变速直线运动。
2.公式的意义:公式2ax=
反映了初速度v0、末速度vt、加速度a、位移x
之间的关系,当其中三个物理量已知时,可求另一个未知量。
3.公式的矢量性:公式中v0、vt、a、x都是矢量,应用时必须选取统一的正方向,
一般选v0方向为正方向。
(1)物体做加速运动时,a取正值,做减速运动时,a取负值。
(2)x>0,说明物体通过的位移方向与初速度方向相同;x<0,说明位移的方向与初
速度的方向相反。
4.两种特殊形式:
(1)当v0=0时,
=2ax(初速度为零的匀加速直线运动)。
(2)当vt=0时,-
=2ax(末速度为零的匀减速直线运动)。
【问题探究】
观察图,思考下列问题。
提示:由v=at得t=
s=18
s,
位移x=
=3
240
m。
【典例示范】
【典例】随着机动车数量的增加,交通安全问题日益凸显。分析交通违法事例,将警示我们遵守交通法规,珍惜生命。一货车严重超载后的总质量为49
t,以
54
km/h的速率匀速行驶。发现红灯时司机刹车,货车立即做匀减速直线运动,加速度的大小为2.5
m/s2(不超载时则为5
m/s2)。
(1)若前方无阻挡,问从刹车到停下来此货车在超载及不超载时分别前进多远?
(2)若超载货车刹车时正前方25
m处停着总质量为1
t的轿车,两车将发生碰撞,求相撞时货车的速度。
【解析】(1)设货车刹车时速度大小为v0,加速度大小为a,末速度大小为v,刹车
距离为x,根据匀变速直线运动的速度与位移的关系式得x=
由题意知,v0=54
km/h=15
m/s,v=0,a1=2.5
m/s2,a2=5
m/s2
代入数据得,超载时x1=45
m
不超载时x2=22.5
m
(2)超载货车与轿车碰撞时,由
=-2ax知
相撞时货车的速度
vt=
m/s=10
m/s
答案:(1)45
m 22.5
m (2)10
m/s
【素养训练】
1.(2020·泰安高一检测)做匀加速直线运动的物体,速度从v增加到3v时经过的
位移是x,则它的速度从3v增加到5v时经过的位移是
( )
A.
x
B.
x
C.
x
D.2x
【解析】选D。根据速度—位移公式得(3v)2-v2=2ax,(5v)2-(3v)2=2ax′,联立两式解得x′=2x,故选项D正确。
2.一物体从静止开始以a1=6
m/s2做匀加速直线运动,通过的距离为x1,所用时间
为t1,达到某一速度后立即开始做匀减速直线运动直至速度为零,减速阶段的加
速度大小为a2=8
m/s2,通过的距离为x2,所用时间为t2。则下列说法正确的是
( )
A.x1∶x2=3∶
4,t1∶t2=3∶4
B.
x1∶x2=3∶4,t1∶t2=4∶3
C.x1∶x2=4∶3,t1∶t2=3∶4
D.x1∶x2=4∶3,t1∶t2=4∶3
【解析】选D。由题意得:x1=
,x2=
,则两式相比得到:
,由
v=at得
,故D正确,A、B、C错误;故选D。
知识点二 六个比例式
初速度为零的匀加速直线运动的常用推论
(1)等分运动时间(以T为时间单位)。
①1T末、2T末、3T末…瞬时速度之比:
由v=at可得:v1∶v2∶v3…=1∶2∶3…
②1T内、2T内、3T内…位移之比:
由x=
at2可得:x1∶x2∶x3…=1∶4∶9…
③第一个T内、第二个T内、第三个T内…的位移之比:
由xⅠ=x1,xⅡ=x2-x1,xⅢ=x3-x2…可得:
xⅠ∶xⅡ∶xⅢ…=1∶3∶5…
(2)等分位移(以x为单位)。
①通过x、2x、3x…所用时间之比:
由x=
at2可得t=
,所以
t1∶t2∶t3…=1∶
∶
…
②通过第一个x、第二个x、第三个x…所用时间之比:
由tⅠ=t1,tⅡ=t2-t1,tⅢ=t3-t2…可得:
tⅠ∶tⅡ∶tⅢ…=1∶(
-1)∶(
-
)…
③x末、2x末、3x末…的瞬时速度之比:
由v2=2ax可得v=
,所以
v1∶v2∶v3…=1∶
∶
…
【典例示范】
【典例】(多选)(2020·南通高一检测)一观察者站在第一节车厢前端,当列车
从静止开始做匀加速运动时(设每节车厢的长度相同,车厢间间隙可以不计)
( )
A.每节车厢末端经过观察者的速度之比是1∶
∶
∶…∶
B.每节车厢末端经过观察者的速度之比是1∶2∶3∶…∶n
C.在相等时间里经过观察者的车厢数之比是1∶3∶5∶…
D.在相等时间里经过观察者的车厢数之比是1∶2∶3∶…
【解析】选A、C。设每节车厢长为l,由v2=2ax得第一节车厢末端经过观察者时
v1=
,同理,第二节车厢末端经过观察者时v2=
……第n节车厢末端经
过观察者时,vn=
,所以有v1∶v2∶v3∶…∶vn=1∶
∶
∶…∶
,选
项A正确;相等时间里经过观察者的车厢数之比是1∶3∶5∶…,选项C正确。
【规律方法】处理直线运动的方法口诀
运用一般公式法,平均速度是简法。
中间时刻速度法,初速度为零比例法。
若是相邻等时间,位移逐差是妙法。
再加几何图像法,求解运动好方法。
【素养训练】一个物体从静止开始做匀加速直线运动,它在第1
s内与第2
s内
的位移之比为x1∶x2,在走完第1
m时与走完第2
m时的速度之比为v1∶v2。以下
说法正确的是
( )
A.x1∶x2=1∶3,v1∶v2=1∶2
B.x1∶x2=1∶3,v1∶v2=1∶
C.x1∶x2=1∶4,v1∶v2=1∶2
D.x1∶x2=1∶4,v1∶v2=1∶
【解析】选B。由初速度为零的匀变速直线运动的比例关系知x1∶x2=1∶3,由x=
at2知,走完1
m与走完2
m所用时间之比为t1∶t2=1∶
,又v=at,可得
v1∶v2=1∶
,选项B正确。
【加固训练】
飞机、火车、汽车等交通工具由静止到稳定运动的过程都可以看作初速度为零的匀加速直线运动。若一辆汽车从静止开始做匀加速直线运动,则求汽车:
(1)1
s末、2
s末、3
s末瞬时速度之比。
(2)1
s内、2
s内、3
s内的位移之比。
(3)第1
s内、第2
s内、第3
s内的位移之比。
(4)经过连续相等的位移,如经过第一个x、第二个x、第三个x所用时间之比。
【解析】(1)由v=at知:v1∶v2∶v3=1∶2∶3;
(2)由x=
at2得:x1∶x2∶x3=1∶22∶32=1∶4∶9;
(3)第1
s内位移xⅠ=
a×12
第2
s内位移xⅡ=
a×22-
a×12=
a×3
第3
s内位移为xⅢ=
a×32-
a×22=
a×5
故xⅠ∶xⅡ∶xⅢ=1∶3∶5;
(4)由x=
a
得第一个x所用时间tⅠ=
。
前2x所用时间t2=
故第二个x所用时间为
tⅡ=t2-tⅠ=(
-1)
同理第三个x所用时间tⅢ=(
-
)
所以有tⅠ∶tⅡ∶tⅢ=1∶(
-1)∶(
-
)。
答案:(1)1∶2∶3 (2)1∶4∶9 (3)1∶3∶5
(4)1∶(
-1)∶(
-
)
【拓展例题】考查内容:运动学公式的选择
【典例】如图所示,在成都天府大道某处安装了一台500万像素的固定雷达测速仪,可以准确抓拍超速车辆以及测量运动车辆的加速度。一辆汽车正从A点迎面驶向测速仪B,若测速仪与汽车相距355
m,此时测速仪发出超声波,同时车由于紧急情况而急刹车,汽车运动到C处与超声波相遇,当测速仪接收到反射回来的超声波信号时,汽车恰好停止于D点,且此时汽车与测速仪相距335
m,忽略测速仪安装高度的影响,可简化为如图所示分析(已知超声波速度为340
m/s)。
(1)求汽车刹车过程中的加速度a的大小。
(2)此路段有80
km/h的限速标志,分析该汽车刹车前的行驶速度是否超速。
【解析】(1)设超声波往返的时间为2t,汽车在2t时间内,刹车的位移为s=
a(2t)2=20
m,
当超声波与车相遇后,车继续前进的时间为t,位移为s2=
at2=5m,则超声波在2t内的路程为2×(335+5)
m=680
m,由声速为340
m/s,得
t=1
s,解得汽车的加速度a=10
m/s2
(2)车刹车过程中的位移s=
,
解得刹车前的速度v0=20
m/s=72
km/h
车速在规定范围内,不超速。
答案:(1)10
m/s2 (2)见解析
【生活情境】
冰壶(Curling),又称掷冰壶、冰上溜石,是以队为单位在冰上进行的一种投掷
性竞赛项目,冬奥会比赛项目,并设有冰壶世锦赛。冰壶周长约为91.44厘米,高
(从壶的底部到顶部)11.43厘米,重量(包括壶柄和壶栓)最大为19.96千克。刷
冰是为了减小冰壶与冰面间摩擦。
情境·模型·素养
探究:如图所示,一冰壶以速度v垂直进入两个相同的矩形区域做匀减速运动,且
刚要离开第二个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的
速度之比和穿过每个矩形区域所用的时间之比分别是多少?(冰壶可看成质点)
【解析】把冰壶的运动看成逆向的初速度为零的匀加速直线运动。冰壶通过两
矩形区域位移相等,则从右向左穿过矩形区域的速度之比为1∶
,则冰壶实际
运动依次进入每个矩形区域的速度之比为v1∶v2=
∶1;冰壶从右向左,通过每
个矩形区域的时间之比为1∶(
-1),则冰壶实际运动穿过区域的时间之比为
t1∶t2=(
-1)∶1。
答案:
∶1 (
-1)∶1
【生活情境】
冬天雾霾活动频繁,空气能见度降低,汽车沿平直公
路匀速行驶,遇到紧急情况
刹车,为避免发生事故,速度不宜过快。
探究:(1)若刹车加速度a恒定,刹车距离x跟速度v有
什么关系?
(2)某汽车在高速公路上行驶,若速度从70
km/h提速到100
km/h,问刹车距离变
成原来的多少倍?
【解析】(1)刹车距离跟速度的关系x=
。
(2)根据上式得,刹车距离变成原来的
倍。
答案:(1)x=
(2)
倍
课堂检测·素养达标
1.F1是英文Formula
One的缩写,即一级方程式赛车,是仅次于奥运会和世界杯的世界第三大赛事,假设赛车起动时加速度为5
m/s2,最大速度可达216
km/h,加速过程可以近似为匀加速直线运动,则赛车加速阶段的位移的大小是
( )
A.360
m
B.36
m
C.720
m
D.72
m
【解析】选A。由题意加速度a=5
m/s2,初速度v0=0,末速度v=216
km/h=
60
m/s。由x=
m=360
m,A正确。
2.一个物体沿着斜面从静止滑下做匀变速直线运动。已知它前2
s内的位移为
3
m,则它在第四个2
s内的位移是
( )
A.14
m B.21
m
C.24
m
D.48
m
【解析】选B。前2
s内的位移x1与第四个2
s内的位移x2之比x1∶x2=1∶(2×4-1)=1∶7,因为x1=3
m,所以x2=21
m,故B正确。
3.从静止开始做匀加速直线运动的物体,在第1
s内、第2
s内、第3
s内的平均
速度之比为
( )
A.1∶3∶5
B.1∶4∶9
C.1∶2∶3
D.1∶
∶
【解析】选A。由于第1
s内、第2
s内、第3
s内的位移之比x1∶x2∶x3
=1∶3∶5,而平均速度v=
,三段时间都是1
s,故三段时间的平均速
度之比为1∶3∶5,则A正确,B、C、D错误。
4.(多选)(教材二次开发·教材P46自我评价T1拓展变式)某汽车沿一直线运动,
在t时间内通过的位移为L,在
处速度为v1,在
处速度为v2,则
( )
A.匀加速运动,v1>v2
B.匀加速运动,v1
【解析】选A、D。设汽车的初速度为v0,末速度为v,则在中间时刻时速度
v2=
,根据位移与时间公式可得
解得在中间位置时
的速度为v1=
,根据数学知识可得
>0,即无论汽车做匀加速运动还是匀减速运动,都有v1>v2,A、D正确。
本题也可以通过v-t图像解决问题,如图所示
5.舰载机在航母跑道上从静止开始做匀加速直线运动,以5
m/s2
的加速度运动,
需要达到50
m/s
的速度才可升空,如图所示。求:
(1)滑行5
s后,舰载机的速度大小?
(2)从启动到起飞,至少滑行多长时间?
(3)航母跑道至少多长?
【解析】(1)由匀变速直线运动规律得v=at=25
m/s;
(2)由匀变速直线运动规律得vm=at1,t1=10
s;
(3)由匀变速直线运动规律得
x=
m=250
m。
答案:(1)25
m/s (2)10
s (3)250
m
【加固训练】
一列火车进站前先关闭气阀,让车减速滑行,滑行了300
m
时速度减为关闭气阀时的一半,此后又继续滑行了20
s停在车站。设火车在滑行过程中加速度始终维持不变,试求:
(1)火车滑行的加速度大小。
(2)火车关闭气阀时的速度大小。
(3)从火车关闭气阀到停止滑行时,滑行的总位移。
【解析】设火车的加速度为a,初速度为v0,由位移与速度关系式得:(
)2-
=2ax1
①
由速度公式得:
0=
+at2
②
代入数据解①②得v0=20
m/s
a=-0.5
m/s2
由速度与位移的关系式得:2ax2=(
)2
代入数据解得x2=100
m
所以总位移
x=x1+x2=300
m+100
m=400
m
答案:(1)0.5
m/s2 (2)20
m/s (3)400
m
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
