数学 五年级上6 多边形的面积课件 冀教版(29张ppt)
文档属性
| 名称 | 数学 五年级上6 多边形的面积课件 冀教版(29张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 447.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
多边形面积
目
录
概
念
长方形面积
平行四边形面积
三角形面积
梯形面积
组合图形面积
相关概念
1、面积的概念:是一个用作表示一个曲面或平面图形所占范围的量,即一个曲面或平面的大小,如我们所说的一张A4纸的大小指的就是它的面积。
1cm
1cm
2、面积的单位:
单位面积是指边长为1的正方形所占范围的量,这个1可以代表1厘米、1分米或者1米、1千米等,如上图边长为1厘米的正方形,它的面积为1平方厘米。
面积单位是指单位长度的平方,如:平方米、平方厘米、平方公里(千米)等,或用m2
、cm2
、km2
、dm2
、mm2
等表示。
3、单位间换算:
1平方千米=106平方米
1平方米=100平方分米
1平方分米=100平方厘米
1平方厘米=100平方毫米
4、研究方法:通过面积的概念和单位,容易想到用计算的方法来研究面积,而测量法,单位面积平铺法,拼接法等都是为最后计算服务的方法。
5、引申:一个点移动所形成的轨迹是线,一条线移动形成的图形就是面,面移动形成体(积)。线是一维空间范畴,面研究的是二维空间,体则是三维空间的体现。
这一部分重点理解单位面积中1的含义
相关概念
长(正)方形面积
正方形是相邻边长相等的特殊长方形,因此,长方形面积计算方法适用于正方形。
一、拼图法:
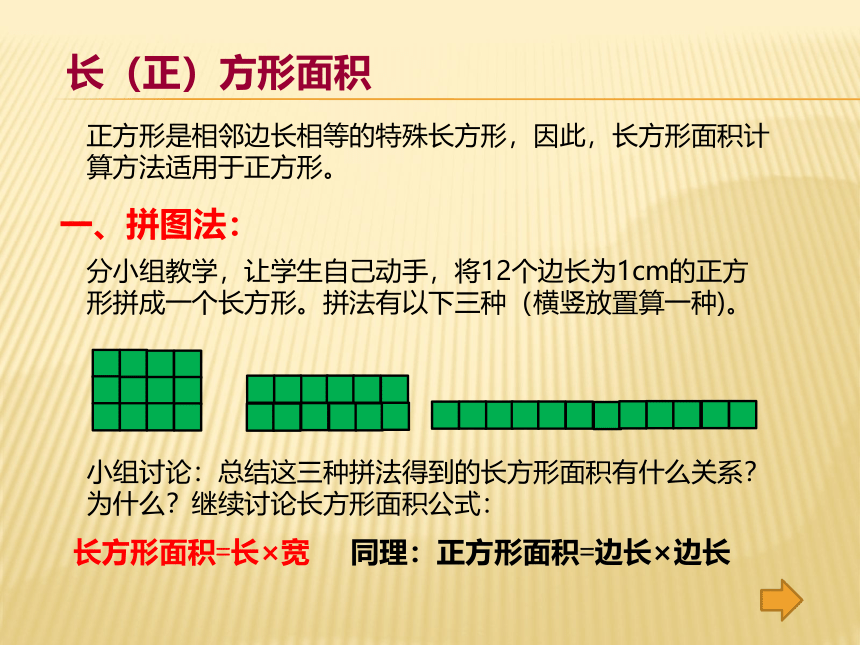
分小组教学,让学生自己动手,将12个边长为1cm的正方形拼成一个长方形。拼法有以下三种(横竖放置算一种)。
小组讨论:总结这三种拼法得到的长方形面积有什么关系?为什么?继续讨论长方形面积公式:
长方形面积=长×宽
同理:正方形面积=边长×边长
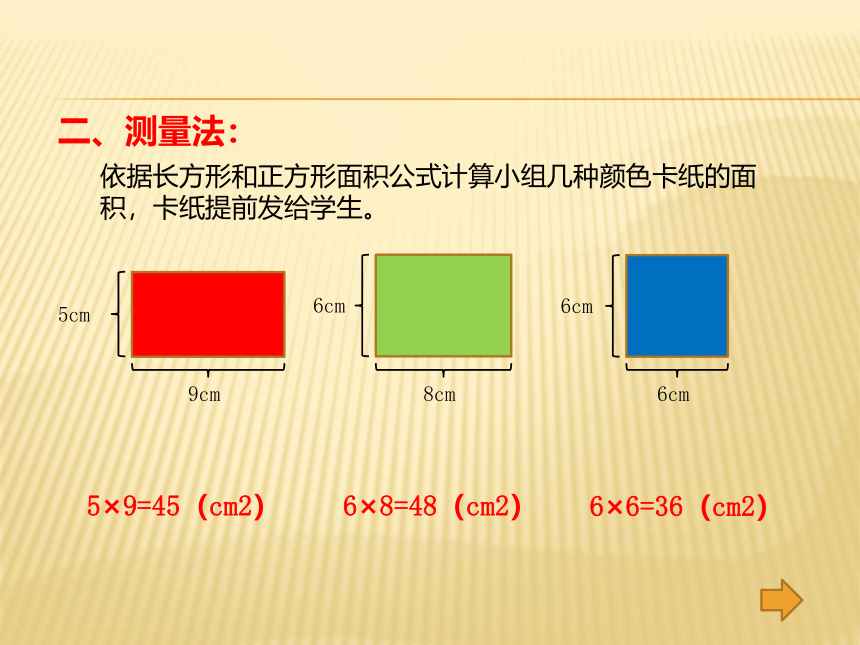
二、测量法:
依据长方形和正方形面积公式计算小组几种颜色卡纸的面积,卡纸提前发给学生。
5cm
9cm
6cm
8cm
6cm
6cm
5×9=45(cm2)
6×8=48(cm2)
6×6=36(cm2)
三、练习:
1、学校的篮球场地长28米,宽15米,计算篮球场地的面积?
28×15=420(平方米)
答:学校篮球场面积为420平方米。
2、把一个长为13厘米,宽为8厘米的长方形,剪去一个最大的正方形,剩下的长方形的面积是多少?
分析:长方形剪去最大正方形,正方形边长以长方形的宽为准,所以剩下的长方形长为8厘米,宽为13-8=5厘米。
8×(13-8)
=8×5
=40(cm2
)
答:剩下长方形面积为40平方米。
8cm
13cm
8cm
5cm
四、小结:
1、在计算长方形或正方形面积时,重点要找准长和宽(边长)。
2、在图形拼接或剪切的时候,要尽量在草稿纸上作图确定长和宽。
3、注意,长和宽的单位要保持一致,若不一致,要进行单位换算。
平行四边形面积
一、引入:
问题一:观察平行四边形,说出平行四边形的特点?
平行四边形是两组平行且相等的线段组成的封闭图形。
问题二:与正方形有什么异同?
相同点:
正方形也是由两组平行且相等的线段组成的封闭图形。
不同点:
正方形的四个角都是90度,而平行四边形的角不是。
问题三:观察下面三个临边相等的平行四边形,想一想它们的面积可以用长方形的面积公式计算吗?为什么?
由上图可以看出平行四边形相邻的两个边夹角越小,面积越小,当夹角接近0度时,面积也趋近于0。因此平行四边形面积不能用相邻的两个边相乘来计算面积,那么它的面积究竟与什么有关?
1m
1m
1m
1m
1m
1m
二、讲解:
观察下面平行四边形,在面积相等情况下,如何将下图中的平行四边形转换成长方形?
由上图可以看出平行四边形的面积与平行四边的一个边与这个边上的高相关,面积公式如下:
面积=底边×高
或
S=ah
三、练习:
一个停车位是平行四边形,它的底长5m,高2.5m,它的面积是多少?
S=ah
=5×2.5
=12.5(m2
)
答:停车场的面积为12.5平方米。
四、小结:
1、平行四边形与长方形的关系,理解长方形是特殊的平行四边形。
2、平行四边形转换成长方形的方法有多种。
3、平行四边形可以做出两条不同的高线。
4、平行四边形的面积公式:面积=底×高
三角形面积
一、引入:
问题一:观察下面的直角三角形和长方形有什么关系?
可以看出长方形可以由两个一样的直角三角形组成,因此直角三角形的面积就应该等于长方形面积的一半,也就是两个直角边乘积的一半,即
面积=直角边×直角边÷2
二、讲解:
问题二:两个相同的非直角三角形(锐角和钝角)可以组合成什么图形?
两个相同非直角三角形可以组成平行四边形,因此三角形的面积等于平行四边形面积的一半,平行四边形的底等于三角形的底,高等于三角形的高,即
面积=底边×高÷2
或
S=ah÷2
问题三:问题一得出的结论是正确的吗?为什么?
因为直角三角形两个直角边互为高线,因此,问题一的结论也是正确的。
问题四:观察右侧三角形的变换,说一说拼成的长方形与三角形有什么关系?
三角形中位线等于底边长度的一半,长方形的长等于三角形的高,长方形的宽等于三角形的中位线,等于三角形底边的一半,即:
三角形面积=长方形面积=中位线×高
三角形面积=底边÷2
×高
三、三角形的高:
请画出下面三角形的高线
通过作图可知:
1、三角形高线的做法是通过一个顶点作对边或对边延长线的垂线。
2、锐角三角形,三条高线在三角形内部,直角三角形两条高线与直角边重合,钝角三角形有两条高在三角形外部。
3、三角形有三条不同的高线,并且三条高线或高线的延长线相较于一点。
四、练习:
1、求出下面三角形的面积。
2、动手量一量我们的红领巾,计算出它的面积。
3、一块三角形地种玉米,它的底长28米,高是20米,如果每平方米可收玉米8千克,这块地可收玉米多少千克?
S=ah÷2
=28×20÷2
=280m2
S=ah÷2
=12×8÷2
=48cm2
280×8=2240(千克)
答:这块地可以收玉米2240千克。
8cm
12cm
五、小结:
1、理解三角形是平行四边形的一半。
2、掌握三角形三条高线的作图方法。
3、合理利用三角形中位线解决问题。
4、三角形的面积公式:面积=底边×高÷2
梯形面积
一、引入:
利用学过的三角形面积解决方法,将下面的梯形转换成已学过的图形。
问题一:拼成的平行四边形与原来的梯形有什么关系?
平行四边形的面积是梯形面积的两倍
问题二:计算平行四边形的面积,底和高如何得到?
平行四边形的底等于梯形的上底加下底的长度
平行四边形的高等于梯形的高
二、讲解:
平行四边形面积=
底
×
高
平行四边形面积=(上底+下底)×
高
梯形面积=(上底+下底)×
高
÷
2
观察右图梯形,借鉴三角形中位线转换方法作图:
长方形的长等于梯形的中位线,中位线的长等于上底加下底除以2。
长方形面积=
长
×
宽
梯形面积=(上底+下底)÷2
×
高
三、练习:
1、计算下面梯形的面积。
(13+21)×8÷2
=24×8÷2
=96m2
2、小明家有块梯形的麦田,上底长28米,下底长32米,高19.5米,请帮助小明计算出这块麦田的面积。
(28+32)×19.5÷2
=60×19.5÷2
=585m2
答:小明家麦田的面积为585平方米。
8m
21m
13m
四、小结:
1、理解梯形与平行四边形的关系。
2、掌握梯形面积的两种推导方式。
3、梯形面积公式:面积=(上底+下底)×高÷2
组合图形的面积
一、引入:
到现在为止,我们已经学过了那些平面图形?它们的面积公式是什么?
长方形
正方形
平行四边形
三角形
梯形
=长×宽
=边长2
=底×高
=底×高÷2
=(上底+下底)×高÷2
利用学过的知识,计算图形的面积,并说说你是怎么想的?
将图形分割成一个长方形和一个直角三角形。
S=S长方形
+S三角形
=6×8+(10-6)×(8-5)÷2
=48+6
54(平方米)
8m
10m
5m
6m
将一个图形分割成多个基本图形的方法叫做“分割法”,把这几个基本图形的面积加起来,就是这个组合图形的面积。
分割法的应用,观察下图看看有几种分割方法?并计算面积。
通过上题可以看出,不同的分割方法最终得到的结果都是相同的。分割法是几何中经常使用的一种方法。
②S=S大长方形
+S小长方形
=6×4+(7-4)×3
=24+9
=33cm2
①
S=S大长方形
+S小长方形
=7×3+(6-3)×4
=21×12
=33cm2
③S=S上梯形
+S下梯形
=[(6-3)+6]×4÷2+[(7-4)+7]×3÷2
=9×4÷2+10×3÷2
=18+15
=33cm2
4cm
6cm
7cm
3cm
二、分割法:
观察下面的图形,试计算它的面积
通过观察我们可以发现,若剪下右侧的三角形,正好可以添补到左侧三角形的空白处,这样就够成一个完整的正方形了。因此,这个图形的面积就等于正方形的面积了。
S=边长2
=142
=196(cm2
)
将图形的一部分分割出来,填补到图形相应位置,组合成一个基本图形的方法,叫“割补法”。
思考:在什么情况下使用与这种方法?
分割出的部分,正好能够填补成一个完整的基本图形
三、割补法:
计算少先队中队旗的面积,说一说你是怎么想的。
S=
S长方形
-S三角形
=80×60-60×20÷2
=4800-600
=4200(cm2
)
答:少先队中队旗的面积为4200平方厘米。
现将中队旗看成一个长方形,再减去右边缺少的三角形。
像这样现将多边形填补成整体,再减去填补部分的方法叫“填补法”。“填补法”是计算几何图形面积时经常使用的方法。
四、填补法:
五、小结:
1、在本章重点要学会用数学思维考虑问题,将复杂的问题简单化。
2、掌握用“分割法”、“填补法”和“割补法”等方法将组合图形转换为简单的基本图形计算。
3、注意:图形转换后要保证原有图形的面积不变。
总
结
1、本课件讲小学多边形面积公式及公式的推导过程。
2、使学生会用数学思维考虑问题,将复杂的问题简单化。
3、重点要求学生掌握通过图形变换来解决实际问题。
多边形面积
目
录
概
念
长方形面积
平行四边形面积
三角形面积
梯形面积
组合图形面积
相关概念
1、面积的概念:是一个用作表示一个曲面或平面图形所占范围的量,即一个曲面或平面的大小,如我们所说的一张A4纸的大小指的就是它的面积。
1cm
1cm
2、面积的单位:
单位面积是指边长为1的正方形所占范围的量,这个1可以代表1厘米、1分米或者1米、1千米等,如上图边长为1厘米的正方形,它的面积为1平方厘米。
面积单位是指单位长度的平方,如:平方米、平方厘米、平方公里(千米)等,或用m2
、cm2
、km2
、dm2
、mm2
等表示。
3、单位间换算:
1平方千米=106平方米
1平方米=100平方分米
1平方分米=100平方厘米
1平方厘米=100平方毫米
4、研究方法:通过面积的概念和单位,容易想到用计算的方法来研究面积,而测量法,单位面积平铺法,拼接法等都是为最后计算服务的方法。
5、引申:一个点移动所形成的轨迹是线,一条线移动形成的图形就是面,面移动形成体(积)。线是一维空间范畴,面研究的是二维空间,体则是三维空间的体现。
这一部分重点理解单位面积中1的含义
相关概念
长(正)方形面积
正方形是相邻边长相等的特殊长方形,因此,长方形面积计算方法适用于正方形。
一、拼图法:
分小组教学,让学生自己动手,将12个边长为1cm的正方形拼成一个长方形。拼法有以下三种(横竖放置算一种)。
小组讨论:总结这三种拼法得到的长方形面积有什么关系?为什么?继续讨论长方形面积公式:
长方形面积=长×宽
同理:正方形面积=边长×边长
二、测量法:
依据长方形和正方形面积公式计算小组几种颜色卡纸的面积,卡纸提前发给学生。
5cm
9cm
6cm
8cm
6cm
6cm
5×9=45(cm2)
6×8=48(cm2)
6×6=36(cm2)
三、练习:
1、学校的篮球场地长28米,宽15米,计算篮球场地的面积?
28×15=420(平方米)
答:学校篮球场面积为420平方米。
2、把一个长为13厘米,宽为8厘米的长方形,剪去一个最大的正方形,剩下的长方形的面积是多少?
分析:长方形剪去最大正方形,正方形边长以长方形的宽为准,所以剩下的长方形长为8厘米,宽为13-8=5厘米。
8×(13-8)
=8×5
=40(cm2
)
答:剩下长方形面积为40平方米。
8cm
13cm
8cm
5cm
四、小结:
1、在计算长方形或正方形面积时,重点要找准长和宽(边长)。
2、在图形拼接或剪切的时候,要尽量在草稿纸上作图确定长和宽。
3、注意,长和宽的单位要保持一致,若不一致,要进行单位换算。
平行四边形面积
一、引入:
问题一:观察平行四边形,说出平行四边形的特点?
平行四边形是两组平行且相等的线段组成的封闭图形。
问题二:与正方形有什么异同?
相同点:
正方形也是由两组平行且相等的线段组成的封闭图形。
不同点:
正方形的四个角都是90度,而平行四边形的角不是。
问题三:观察下面三个临边相等的平行四边形,想一想它们的面积可以用长方形的面积公式计算吗?为什么?
由上图可以看出平行四边形相邻的两个边夹角越小,面积越小,当夹角接近0度时,面积也趋近于0。因此平行四边形面积不能用相邻的两个边相乘来计算面积,那么它的面积究竟与什么有关?
1m
1m
1m
1m
1m
1m
二、讲解:
观察下面平行四边形,在面积相等情况下,如何将下图中的平行四边形转换成长方形?
由上图可以看出平行四边形的面积与平行四边的一个边与这个边上的高相关,面积公式如下:
面积=底边×高
或
S=ah
三、练习:
一个停车位是平行四边形,它的底长5m,高2.5m,它的面积是多少?
S=ah
=5×2.5
=12.5(m2
)
答:停车场的面积为12.5平方米。
四、小结:
1、平行四边形与长方形的关系,理解长方形是特殊的平行四边形。
2、平行四边形转换成长方形的方法有多种。
3、平行四边形可以做出两条不同的高线。
4、平行四边形的面积公式:面积=底×高
三角形面积
一、引入:
问题一:观察下面的直角三角形和长方形有什么关系?
可以看出长方形可以由两个一样的直角三角形组成,因此直角三角形的面积就应该等于长方形面积的一半,也就是两个直角边乘积的一半,即
面积=直角边×直角边÷2
二、讲解:
问题二:两个相同的非直角三角形(锐角和钝角)可以组合成什么图形?
两个相同非直角三角形可以组成平行四边形,因此三角形的面积等于平行四边形面积的一半,平行四边形的底等于三角形的底,高等于三角形的高,即
面积=底边×高÷2
或
S=ah÷2
问题三:问题一得出的结论是正确的吗?为什么?
因为直角三角形两个直角边互为高线,因此,问题一的结论也是正确的。
问题四:观察右侧三角形的变换,说一说拼成的长方形与三角形有什么关系?
三角形中位线等于底边长度的一半,长方形的长等于三角形的高,长方形的宽等于三角形的中位线,等于三角形底边的一半,即:
三角形面积=长方形面积=中位线×高
三角形面积=底边÷2
×高
三、三角形的高:
请画出下面三角形的高线
通过作图可知:
1、三角形高线的做法是通过一个顶点作对边或对边延长线的垂线。
2、锐角三角形,三条高线在三角形内部,直角三角形两条高线与直角边重合,钝角三角形有两条高在三角形外部。
3、三角形有三条不同的高线,并且三条高线或高线的延长线相较于一点。
四、练习:
1、求出下面三角形的面积。
2、动手量一量我们的红领巾,计算出它的面积。
3、一块三角形地种玉米,它的底长28米,高是20米,如果每平方米可收玉米8千克,这块地可收玉米多少千克?
S=ah÷2
=28×20÷2
=280m2
S=ah÷2
=12×8÷2
=48cm2
280×8=2240(千克)
答:这块地可以收玉米2240千克。
8cm
12cm
五、小结:
1、理解三角形是平行四边形的一半。
2、掌握三角形三条高线的作图方法。
3、合理利用三角形中位线解决问题。
4、三角形的面积公式:面积=底边×高÷2
梯形面积
一、引入:
利用学过的三角形面积解决方法,将下面的梯形转换成已学过的图形。
问题一:拼成的平行四边形与原来的梯形有什么关系?
平行四边形的面积是梯形面积的两倍
问题二:计算平行四边形的面积,底和高如何得到?
平行四边形的底等于梯形的上底加下底的长度
平行四边形的高等于梯形的高
二、讲解:
平行四边形面积=
底
×
高
平行四边形面积=(上底+下底)×
高
梯形面积=(上底+下底)×
高
÷
2
观察右图梯形,借鉴三角形中位线转换方法作图:
长方形的长等于梯形的中位线,中位线的长等于上底加下底除以2。
长方形面积=
长
×
宽
梯形面积=(上底+下底)÷2
×
高
三、练习:
1、计算下面梯形的面积。
(13+21)×8÷2
=24×8÷2
=96m2
2、小明家有块梯形的麦田,上底长28米,下底长32米,高19.5米,请帮助小明计算出这块麦田的面积。
(28+32)×19.5÷2
=60×19.5÷2
=585m2
答:小明家麦田的面积为585平方米。
8m
21m
13m
四、小结:
1、理解梯形与平行四边形的关系。
2、掌握梯形面积的两种推导方式。
3、梯形面积公式:面积=(上底+下底)×高÷2
组合图形的面积
一、引入:
到现在为止,我们已经学过了那些平面图形?它们的面积公式是什么?
长方形
正方形
平行四边形
三角形
梯形
=长×宽
=边长2
=底×高
=底×高÷2
=(上底+下底)×高÷2
利用学过的知识,计算图形的面积,并说说你是怎么想的?
将图形分割成一个长方形和一个直角三角形。
S=S长方形
+S三角形
=6×8+(10-6)×(8-5)÷2
=48+6
54(平方米)
8m
10m
5m
6m
将一个图形分割成多个基本图形的方法叫做“分割法”,把这几个基本图形的面积加起来,就是这个组合图形的面积。
分割法的应用,观察下图看看有几种分割方法?并计算面积。
通过上题可以看出,不同的分割方法最终得到的结果都是相同的。分割法是几何中经常使用的一种方法。
②S=S大长方形
+S小长方形
=6×4+(7-4)×3
=24+9
=33cm2
①
S=S大长方形
+S小长方形
=7×3+(6-3)×4
=21×12
=33cm2
③S=S上梯形
+S下梯形
=[(6-3)+6]×4÷2+[(7-4)+7]×3÷2
=9×4÷2+10×3÷2
=18+15
=33cm2
4cm
6cm
7cm
3cm
二、分割法:
观察下面的图形,试计算它的面积
通过观察我们可以发现,若剪下右侧的三角形,正好可以添补到左侧三角形的空白处,这样就够成一个完整的正方形了。因此,这个图形的面积就等于正方形的面积了。
S=边长2
=142
=196(cm2
)
将图形的一部分分割出来,填补到图形相应位置,组合成一个基本图形的方法,叫“割补法”。
思考:在什么情况下使用与这种方法?
分割出的部分,正好能够填补成一个完整的基本图形
三、割补法:
计算少先队中队旗的面积,说一说你是怎么想的。
S=
S长方形
-S三角形
=80×60-60×20÷2
=4800-600
=4200(cm2
)
答:少先队中队旗的面积为4200平方厘米。
现将中队旗看成一个长方形,再减去右边缺少的三角形。
像这样现将多边形填补成整体,再减去填补部分的方法叫“填补法”。“填补法”是计算几何图形面积时经常使用的方法。
四、填补法:
五、小结:
1、在本章重点要学会用数学思维考虑问题,将复杂的问题简单化。
2、掌握用“分割法”、“填补法”和“割补法”等方法将组合图形转换为简单的基本图形计算。
3、注意:图形转换后要保证原有图形的面积不变。
总
结
1、本课件讲小学多边形面积公式及公式的推导过程。
2、使学生会用数学思维考虑问题,将复杂的问题简单化。
3、重点要求学生掌握通过图形变换来解决实际问题。
