2020-2021学年山东省潍坊市高二(上)12月月考数学试卷人教B版(Word含解析)
文档属性
| 名称 | 2020-2021学年山东省潍坊市高二(上)12月月考数学试卷人教B版(Word含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 493.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 12:27:05 | ||
图片预览




文档简介
2020-2021学年山东省潍坊市高二(上)12月月考数学试卷
一、选择题
?
1.
点关于平面的对称点为?
?
?
?
A.
B.
C.
D.
?
2.
已知直线的方程为,则直线的倾斜角为(?
?
?
?
)
A.
B.
C.
D.
?
3.
已知,是两条不同的直线,是两个不重合的平面,则下列命题中正确的是?
?
?
?
A.若,则
B.若,则
C.若,则
D.若,则
?
4.
山东省高考改革后实施选科走班制度,小明需要从物理、化学、生物、政治、历史、地理中选择三科作为自己的选科组合,物理和历史不能同时选择,则小明不同的选科情况有(????????)
A.种
B.种
C.种
D.种
?
5.
直线过点且与椭圆相交于,两点,若点为弦的中点,则直线的斜率为?
?
?
?
A.
B.
C.
D.
?
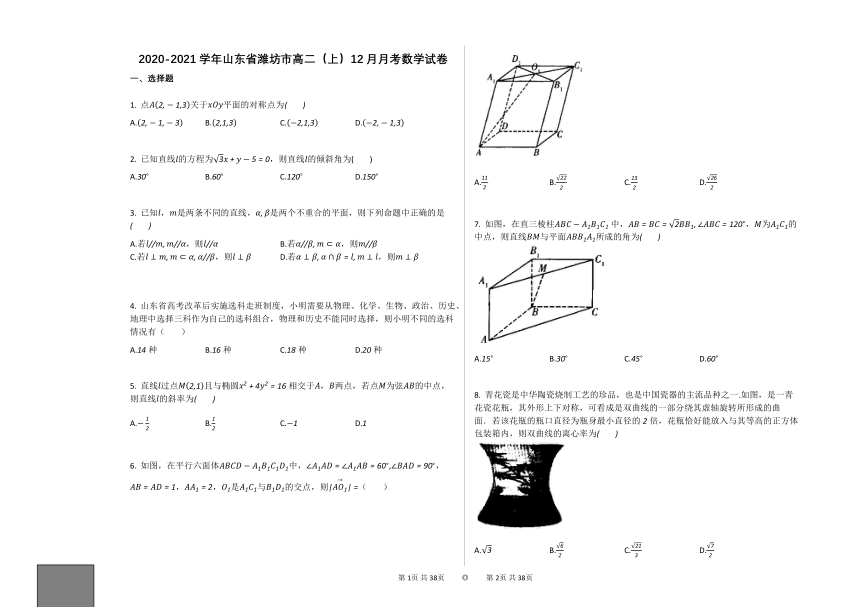
6.
如图,在平行六面体中,,,,,是与的交点,则(????????)
A.
B.
C.
D.
?
7.
如图,在直三棱柱
中,,为的中点,则直线与平面所成的角为?
?
?
?
A.
B.
C.
D.
?
8.
青花瓷是中华陶瓷烧制工艺的珍品,也是中国瓷器的主流品种之一.如图,是一青花瓷花瓶,其外形上下对称,可看成是双曲线的一部分绕其虚轴旋转所形成的曲面.若该花瓶的瓶口直径为瓶身最小直径的倍,花瓶恰好能放入与其等高的正方体包装箱内,则双曲线的离心率为?
?
?
?
A.
B.
C.
D.
二、多选题
?
已知曲线,则下列结论正确的是(?
?
?
?
)
A.若,则曲线表示双曲线
B.曲线可能表示一个圆
C.若曲线是椭圆,则其长轴长为
D.若,则曲线中过焦点的最短弦长为
?
已知曲线上任意一点到直线的距离比它到点的距离大,则下列结论正确的是(????????)
A.曲线的方程为
B.若曲线上的一点到点的距离为,则点的纵坐标是
C.已知曲线上的两点,到点的距离之和为,则线段的中点横坐标是
D.已知,是曲线上的动点,则的最小值为
?
如图,在三棱锥中,平面,,以为直径的圆经过点,,则下列结论正确的是(????????)
A.平面平面
B.三棱锥的体积为
C.二面角的正切值为
D.三棱锥外接球的表面积为
?
如图,是双曲线:的左、右焦点,是圆上一动点,线段的垂直平分线与直线的交点恰好在双曲线上,则下列结论正确的是(????????)
A.双曲线的渐近线方程为
B.双曲线的离心率为
C.焦点到双曲线的渐近线距离为
D.内切圆圆心的横坐标为或
三、填空题
?
计算:?
?
?
??
.
?
已知双曲线的离心率为,则双曲线的渐近线方程为________.
?
已知圆与圆相交于,两点,则?
?
?
??
.
?
如图,正方体的棱长为,,分别为,的中点,则平面截正方体所得的截面面积为________;以点为球心,为半径的球面与对角面的交线长度为________.
四、解答题
?
已知空间中三点,,,设,.
求向量与夹角的余弦值;
若与互相垂直,求实数的值.
?
已知直线与圆交于,两点,
求的值;
求与直线平行的圆的切线方程.
?
从①;②直线与平面所成的角为;③为锐角三角形且三棱锥的体积为这三个条件中任选一个,补充在下面的问题中,并完成解答.
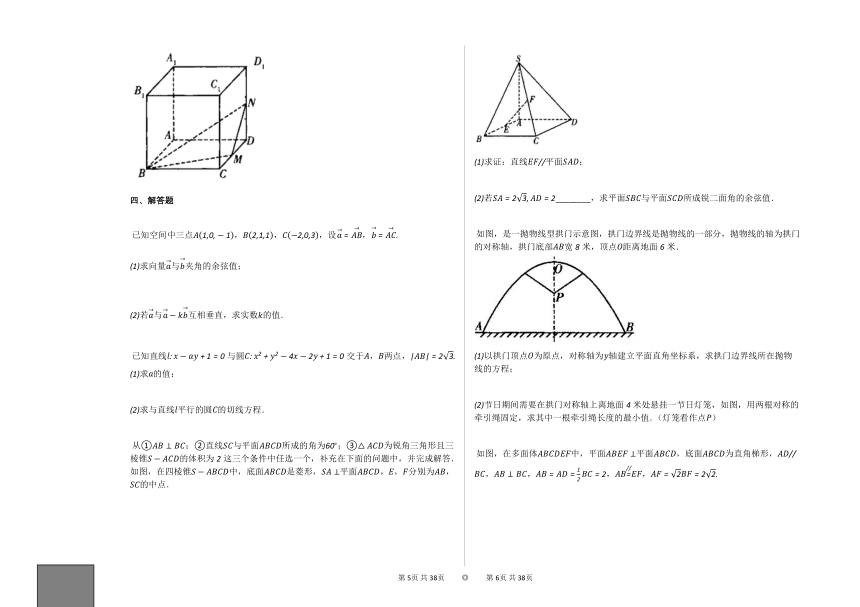
如图,在四棱锥中,底面是菱形,平面,,分别为,的中点.
求证:直线平面;
若________,求平面与平面所成锐二面角的余弦值.
?
如图,是一抛物线型拱门示意图,拱门边界线是抛物线的一部分,抛物线的轴为拱门的对称轴,拱门底部宽米,顶点距离地面米.
以拱门顶点为原点,对称轴为轴建立平面直角坐标系,求拱门边界线所在抛物线的方程;
节日期间需要在拱门对称轴上离地面米处悬挂一节日灯笼,如图,用两根对称的牵引绳固定,求其中一根牵引绳长度的最小值.(灯笼看作点)
?
如图,在多面体中,平面平面,底面为直角梯形,,,,,
证明:;
在线段上是否存在点,使得点到平面的距离为
若存在,求出的值;若不存在,说明理由.
?
已知为椭圆的一个焦点,为椭圆与轴正半轴的交点,椭圆上的点满足.
求椭圆的标准方程;
直线与椭圆相交于,两点,若以为直径的圆经过原点,求证:原点到直线的距离为定值.
参考答案与试题解析
2020-2021学年山东省潍坊市高二(上)12月月考数学试卷
一、选择题
1.
【答案】
A
【考点】
空间中的点的坐标
【解析】
在空间直角坐标系中,任一点关于平面的对称点为.
【解答】
解:在空间直角坐标系中,
任一点关于平面的对称点为,
则点关于平面的对称点为.
故选.?
2.
【答案】
C
【考点】
直线的斜率
【解析】
此题暂无解析
【解答】
解:∵
直线的斜率为:,
设直线的倾斜角为,
所以.
故选.
3.
【答案】
B
【考点】
空间中直线与平面之间的位置关系
命题的真假判断与应用
空间中平面与平面之间的位置关系
【解析】
空间中的线面位置关系,平行和垂直的结论以及面面垂直的判定定理判断
【解答】
解:若,,则或,选项错误;
若,,则,选项正确;
若,,,则或与相交,选项错误;
若,,,则当时,.
当时,与相交但不垂直,选项错误.
故选.
4.
【答案】
B
【考点】
排列、组合及简单计数问题
【解析】
分有物理无历史,无物理有历史,无物理无历史讨论即可.
【解答】
解:当选择的科目有物理无历史时,有种情况;
当选择的科目无物理有历史时,有种情况;
当选择的科目无物理无历史时,有种情况,
小明不同的选科情况有种.
故选.
5.
【答案】
A
【考点】
直线与椭圆的位置关系
直线的斜率
与椭圆有关的中点弦及弦长问题
【解析】
解:设,
由是线段中点得:
,.
又?,
作差可得:,
代入得:,
∴
直线的斜率为.
故选.
【解答】
解:设,
由是线段中点得:
,.
又?,
作差可得:,
将,代入得:,
∴
直线的斜率为.
故选.
6.
【答案】
D
【考点】
棱柱的结构特征
平面向量数量积的运算
【解析】
先由空间向量的基本定理,将向量用一组基底表示,再利用向量数量积的性质计算即可.
【解答】
?解:∵
?
.
∴
?
.
∵
,
∴
,
,
,
?∴
原式
?,
??.
故选.??
7.
【答案】
B
【考点】
直线与平面所成的角
直线与平面垂直的判定
【解析】
由作,垂足为,
由直三棱柱的定义得面,连接,
则为直线与平面所成的角,可得解.
【解答】
解:由作,垂足为,
由直三棱柱的定义得面,连接,如图,
则为直线与平面所成的角,
设,
,
解得.
在,,
,
,
所以,
所以.
故选.
8.
【答案】
C
【考点】
双曲线的定义
双曲线的离心率
【解析】
此题暂无解析
【解答】
解:设双曲线的方程为,
因为该花瓶的瓶口直径为瓶身最小直径的两倍,
所以可得花瓶底面直径为,
因为花瓶恰好能放入与其等高的正方体包装箱,
所以可得该双曲线正好过点,
所以将点代入双曲线方程可得,解得,
所以.
故选.
二、多选题
【答案】
A,D
【考点】
椭圆的定义和性质
双曲线的特性
椭圆的标准方程
圆的标准方程
【解析】
利用双曲线,椭圆,圆的性质对选项一一进行分析解答即可得.
【解答】
解:对:当,则可得,,所以可得曲线表示双曲线,故正确;
对:当,曲线为一个圆,即,
因为,所以无解,
即可得曲线不可能为一个圆,故错误;
对:当时,即时,曲线为椭圆,此时,
所以,
所以椭圆C的长轴为,故错误;
对:当时,可得曲线为椭圆,
所以椭圆的焦点为,
把代入椭圆,即可得,
所以椭圆过焦点最短的弦长为,故正确.
故选.
【答案】
A,B,D
【考点】
点到直线的距离公式
曲线与方程
抛物线的定义
抛物线的应用
【解析】
由抛物线的定义,结合抛物线的相关性质及最值,对四个选项逐一判断即可得到正确答案.
【解答】
解:由题可知,曲线上任意一点到直线的距离与到点的距离相等,
所以曲线的轨迹是以为焦点的抛物线,方程为:,故正确;
由抛物线的定义,到直线的距离为,则点的横坐标为,
代入抛物线方程得纵坐标为,故正确;
设的横坐标为,由抛物线的定义得:,则,
所以线段的中点的横坐标为,故错误;
设点到准线的距离为,由抛物线的定义,,
故正确.
故选.
【答案】
A,C,D
【考点】
直线与平面垂直的性质
直线与平面垂直的判定
球的表面积和体积
【解析】
此题暂无解析
【解答】
解:由题意面,
所以
以为直径的圆过,,
所以面,
面,
可得平面面,故正确.
由,,
,
,故错误.
取的中点,连接,
等边三角形,
,
得为的平面角,
,
故二面角的正切值为,故正确.
由题设三棱锥的外接球直径为,
所以,
.故正确.
故选.
【答案】
B,C,D
【考点】
双曲线的特性
双曲线的标准方程
双曲线的离心率
轨迹方程
圆锥曲线问题的解决方法
点到直线的距离公式
【解析】
此题暂无解析
【解答】
解:由题意得:,,
所以,
所以,
所以,,
,
所以双曲线方程为,
故双曲线的渐近线方程为,故错误;
,故正确;
焦点到双曲线的渐近线距离为,故正确;
设内切圆圆心为,与,,分别相切于,
,,,
所以
,
又,
所以,,圆心横坐标为,
当当交点在坐支上时,同理可得圆心横坐标为,故正确.
故选.
三、填空题
【答案】
【考点】
组合及组合数公式
【解析】
直接组合,排列公式计算即可.
【解答】
解:.
故答案为:.
【答案】
【考点】
双曲线的离心率
双曲线的渐近线
【解析】
结合离心率结合,,之间的关系即可求出结论.
【解答】
解:∵
,
∴
,即,
故双曲线的渐近线方程为.
故答案为:.
【答案】
【考点】
圆与圆的位置关系及其判定
点到直线的距离公式
【解析】
首先求出直线方程,再利用直线与圆相交弦的求法
求解即可.
【解答】
解:把两个圆的方程相减可得直线方程:
,即,
则圆心到直线距离,
故?.
故答案为:.
【答案】
,
【考点】
球的性质
棱柱的结构特征
组合几何体的面积、体积问题
【解析】
由题意作出图形,可得平面截正方体所得截面为等腰梯形
,求出此梯形面积即可,再找出以点M为球心,以为半径的球面与对角面的交线利用弧长公式求解交线长.
【解答】
解:如图,
连接,则,
所以等腰梯形为平面截正方体所得截面图形,
由正方体的棱长为,得,,,
则点到的距离为,
所以,
因为平面平面,且平面平面平面,
过点作于,则平面,
因为点为中点,所以,
以点为球心,以为半径的球面与对角面的交线为圆弧,
其半径为,
由,,得,
所以,
所求交线为劣弧,
长度为,
故答案是.
四、解答题
【答案】
解:因为,,
所以.
,,
所以,
所以与的夹角余弦值为.
,
因为与互相垂直,
所以,解得:,
所以当与互相垂直时,实数的值为.
【考点】
空间向量的数量积运算
用空间向量求直线间的夹角、距离
向量的数量积判断向量的共线与垂直
【解析】
无
无
【解答】
解:因为,,
所以.
,,
所以,
所以与的夹角余弦值为.
,
因为与互相垂直,
所以,解得:,
所以当与互相垂直时,实数的值为.
【答案】
解:圆的方程可化为,
因为,
所以圆心到直线的距离为.
圆心到直线的距离,
所以.
由得直线的方程为.
因为切线与直线平行,
所以设所求的切线方程为.
因为直线与圆相切,
所以圆心到切线的距离.
所以或.
所以所求切线方程为或.
【考点】
圆的标准方程
点到直线的距离公式
直线与圆的位置关系
直线的一般式方程与直线的平行关系
【解析】
无
无
【解答】
解:圆的方程可化为,
因为,
所以圆心到直线的距离为.
圆心到直线的距离,
所以.
由得直线的方程为.
因为切线与直线平行,
所以设所求的切线方程为.
因为直线与圆相切,
所以圆心到切线的距离.
所以或.
所以所求切线方程为或.
【答案】
证明:如图,取的中点为,连接,.
因为,
所以?.?
因为为中点,四边形为菱形,
所以,
所以,
所以四边形为平行四边形,
所以,
因为平面,平面,
以平面.
解:选择条件①:
因为平面,
所以?.?
因为,
所以以为坐标原点,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,,,
所以,,?.?
设平面的一个法向量,
即?
令,则,
设平面的一个法向量,
即
令则,
设平面与平面所成锐二面角为,
则=?.?
所以平面与平面所成锐二面角的余弦值为?.
选条件②:
因为平面,
所以直线与平面所成角为.
因为,
所以,
所以为正三角形.
取中点为,连接,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,
,,,
设平面的一个法向量,
即
令,则,
设平面的一个法向量,
即
令,则,
设平面与平面所成锐二面角为,
则,
所以平面与平面所成锐二面角的余弦值为?
.?
选条件③:
,
所以,
因为,
所以?.?
取中点为,连接,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,
,,,
设平面的一个法向量,
即
令,则,
设平面的一个法向量,
即
令,则,
设平面与平面所成锐二面角为,
则,
所以平面与平面所成锐二面角的余弦值为?
.
【考点】
直线与平面平行的判定
用空间向量求平面间的夹角
【解析】
此题暂无解析
【解答】
证明:如图,取的中点为,连接,.
因为,
所以?.?
因为为中点,四边形为菱形,
所以,
所以,
所以四边形为平行四边形,
所以,
因为平面,平面,
以平面.
解:选择条件①:
因为平面,
所以?.?
因为,
所以以为坐标原点,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,,,
所以,,?.?
设平面的一个法向量,
即?
令,则,
设平面的一个法向量,
即
令则,
设平面与平面所成锐二面角为,
则=
.?
所以平面与平面所成锐二面角的余弦值为?.
选条件②:
因为平面,
所以直线与平面所成角为.
因为,
所以,
所以为正三角形.
取中点为,连接,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,
,,,
设平面的一个法向量,
即
令,则,
设平面的一个法向量,
即
令,则,
设平面与平面所成锐二面角为,
则,
所以平面与平面所成锐二面角的余弦值为?
.?
选条件③:
,
所以,
因为,
所以?.?
取中点为,连接,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,
,,,
设平面的一个法向量,
即
令,则,
设平面的一个法向量,
即
令,则,
设平面与平面所成锐二面角为,
则,
所以平面与平面所成锐二面角的余弦值为?
.
【答案】
解:以抛物线的顶点为坐标原点,抛物线的对称轴为轴,建立平面直角坐标系,如图
.?
则??,
设抛物线的标准方程为,
因为点在抛物线上,?
所以,
解得,
所以抛物线的方程为?.?
设为灯笼所在点,?为抛物线上设置牵引绳的点,
则,
,
当时,的最小值为,
即一条牵引绳长度的最小值为?.?
【考点】
抛物线的标准方程
二次函数在闭区间上的最值
【解析】
(1)以抛物线的顶点为坐标原点,抛物线的对称轴为轴,建立平面直角坐标系,如图
.?则??,
设抛物线的标准方程为,
因为点在抛物线上,?
所以,解得,
所以抛物线的方程为?.?
【解答】
解:以抛物线的顶点为坐标原点,抛物线的对称轴为轴,建立平面直角坐标系,如图
.?
则??,
设抛物线的标准方程为,
因为点在抛物线上,?
所以,
解得,
所以抛物线的方程为?.?
设为灯笼所在点,?为抛物线上设置牵引绳的点,
则,
,
当时,的最小值为,
即一条牵引绳长度的最小值为?.?
【答案】
证明:因为,,,
所以,
所以.
因为平面,
平面,,
所以.
因为,
所以.
解:存在,由知,且,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图.
,,,
,,.
,,
设
(),
则
.
设平面的一个法向量为,
即
令,则,
设点到平面的距离为,
,
解得或(舍).
所以在线段上存在点,且.
【考点】
两条直线垂直的判定
点、线、面间的距离计算
【解析】
无
无
【解答】
证明:因为,,,
所以,
所以.
因为平面,
平面,,
所以.
因为,
所以.
解:存在,由知,且,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图.
,,,
,,.
,,
设
(),
则
.
设平面的一个法向量为,
即
令,则,
设点到平面的距离为,
,
解得或(舍).
所以在线段上存在点,且.
【答案】
解:由题意设椭圆的标准方程为().
则,
因为
,
所以,
因为在椭圆上,
所以,
解得,
所以,
所以椭圆的标准方程为.
证明:①当直线的斜率不存在时,设:,因为,
所以.
因为以为直径的圆过原点,
所以,得,
.
此时原点到直线的距离为.
②当直线的斜率存在时,设:.
由得,
,
得,
设,,
则,,
.
因为以为直径的圆过原点,
所以,
所以.
此时原点到直线的距离.
综上,原点到直线的距离为定值.
【考点】
椭圆的定义和性质
椭圆的标准方程
直线与椭圆结合的最值问题
椭圆的应用
直线与椭圆的位置关系
【解析】
无
无
【解答】
解:由题意设椭圆的标准方程为().
则,
因为
,
所以,
因为在椭圆上,
所以,
解得,
所以,
所以椭圆的标准方程为.
证明:①当直线的斜率不存在时,设:,因为,
所以.
因为以为直径的圆过原点,
所以,得,
.
此时原点到直线的距离为.
②当直线的斜率存在时,设:.
由得,
,
得,
设,,
则,,
.
因为以为直径的圆过原点,
所以,
所以.
此时原点到直线的距离.
综上,原点到直线的距离为定值.
第7页
共20页
◎
第8页
共20页
第9页
共20页
◎
第10页
共20页
一、选择题
?
1.
点关于平面的对称点为?
?
?
?
A.
B.
C.
D.
?
2.
已知直线的方程为,则直线的倾斜角为(?
?
?
?
)
A.
B.
C.
D.
?
3.
已知,是两条不同的直线,是两个不重合的平面,则下列命题中正确的是?
?
?
?
A.若,则
B.若,则
C.若,则
D.若,则
?
4.
山东省高考改革后实施选科走班制度,小明需要从物理、化学、生物、政治、历史、地理中选择三科作为自己的选科组合,物理和历史不能同时选择,则小明不同的选科情况有(????????)
A.种
B.种
C.种
D.种
?
5.
直线过点且与椭圆相交于,两点,若点为弦的中点,则直线的斜率为?
?
?
?
A.
B.
C.
D.
?
6.
如图,在平行六面体中,,,,,是与的交点,则(????????)
A.
B.
C.
D.
?
7.
如图,在直三棱柱
中,,为的中点,则直线与平面所成的角为?
?
?
?
A.
B.
C.
D.
?
8.
青花瓷是中华陶瓷烧制工艺的珍品,也是中国瓷器的主流品种之一.如图,是一青花瓷花瓶,其外形上下对称,可看成是双曲线的一部分绕其虚轴旋转所形成的曲面.若该花瓶的瓶口直径为瓶身最小直径的倍,花瓶恰好能放入与其等高的正方体包装箱内,则双曲线的离心率为?
?
?
?
A.
B.
C.
D.
二、多选题
?
已知曲线,则下列结论正确的是(?
?
?
?
)
A.若,则曲线表示双曲线
B.曲线可能表示一个圆
C.若曲线是椭圆,则其长轴长为
D.若,则曲线中过焦点的最短弦长为
?
已知曲线上任意一点到直线的距离比它到点的距离大,则下列结论正确的是(????????)
A.曲线的方程为
B.若曲线上的一点到点的距离为,则点的纵坐标是
C.已知曲线上的两点,到点的距离之和为,则线段的中点横坐标是
D.已知,是曲线上的动点,则的最小值为
?
如图,在三棱锥中,平面,,以为直径的圆经过点,,则下列结论正确的是(????????)
A.平面平面
B.三棱锥的体积为
C.二面角的正切值为
D.三棱锥外接球的表面积为
?
如图,是双曲线:的左、右焦点,是圆上一动点,线段的垂直平分线与直线的交点恰好在双曲线上,则下列结论正确的是(????????)
A.双曲线的渐近线方程为
B.双曲线的离心率为
C.焦点到双曲线的渐近线距离为
D.内切圆圆心的横坐标为或
三、填空题
?
计算:?
?
?
??
.
?
已知双曲线的离心率为,则双曲线的渐近线方程为________.
?
已知圆与圆相交于,两点,则?
?
?
??
.
?
如图,正方体的棱长为,,分别为,的中点,则平面截正方体所得的截面面积为________;以点为球心,为半径的球面与对角面的交线长度为________.
四、解答题
?
已知空间中三点,,,设,.
求向量与夹角的余弦值;
若与互相垂直,求实数的值.
?
已知直线与圆交于,两点,
求的值;
求与直线平行的圆的切线方程.
?
从①;②直线与平面所成的角为;③为锐角三角形且三棱锥的体积为这三个条件中任选一个,补充在下面的问题中,并完成解答.
如图,在四棱锥中,底面是菱形,平面,,分别为,的中点.
求证:直线平面;
若________,求平面与平面所成锐二面角的余弦值.
?
如图,是一抛物线型拱门示意图,拱门边界线是抛物线的一部分,抛物线的轴为拱门的对称轴,拱门底部宽米,顶点距离地面米.
以拱门顶点为原点,对称轴为轴建立平面直角坐标系,求拱门边界线所在抛物线的方程;
节日期间需要在拱门对称轴上离地面米处悬挂一节日灯笼,如图,用两根对称的牵引绳固定,求其中一根牵引绳长度的最小值.(灯笼看作点)
?
如图,在多面体中,平面平面,底面为直角梯形,,,,,
证明:;
在线段上是否存在点,使得点到平面的距离为
若存在,求出的值;若不存在,说明理由.
?
已知为椭圆的一个焦点,为椭圆与轴正半轴的交点,椭圆上的点满足.
求椭圆的标准方程;
直线与椭圆相交于,两点,若以为直径的圆经过原点,求证:原点到直线的距离为定值.
参考答案与试题解析
2020-2021学年山东省潍坊市高二(上)12月月考数学试卷
一、选择题
1.
【答案】
A
【考点】
空间中的点的坐标
【解析】
在空间直角坐标系中,任一点关于平面的对称点为.
【解答】
解:在空间直角坐标系中,
任一点关于平面的对称点为,
则点关于平面的对称点为.
故选.?
2.
【答案】
C
【考点】
直线的斜率
【解析】
此题暂无解析
【解答】
解:∵
直线的斜率为:,
设直线的倾斜角为,
所以.
故选.
3.
【答案】
B
【考点】
空间中直线与平面之间的位置关系
命题的真假判断与应用
空间中平面与平面之间的位置关系
【解析】
空间中的线面位置关系,平行和垂直的结论以及面面垂直的判定定理判断
【解答】
解:若,,则或,选项错误;
若,,则,选项正确;
若,,,则或与相交,选项错误;
若,,,则当时,.
当时,与相交但不垂直,选项错误.
故选.
4.
【答案】
B
【考点】
排列、组合及简单计数问题
【解析】
分有物理无历史,无物理有历史,无物理无历史讨论即可.
【解答】
解:当选择的科目有物理无历史时,有种情况;
当选择的科目无物理有历史时,有种情况;
当选择的科目无物理无历史时,有种情况,
小明不同的选科情况有种.
故选.
5.
【答案】
A
【考点】
直线与椭圆的位置关系
直线的斜率
与椭圆有关的中点弦及弦长问题
【解析】
解:设,
由是线段中点得:
,.
又?,
作差可得:,
代入得:,
∴
直线的斜率为.
故选.
【解答】
解:设,
由是线段中点得:
,.
又?,
作差可得:,
将,代入得:,
∴
直线的斜率为.
故选.
6.
【答案】
D
【考点】
棱柱的结构特征
平面向量数量积的运算
【解析】
先由空间向量的基本定理,将向量用一组基底表示,再利用向量数量积的性质计算即可.
【解答】
?解:∵
?
.
∴
?
.
∵
,
∴
,
,
,
?∴
原式
?,
??.
故选.??
7.
【答案】
B
【考点】
直线与平面所成的角
直线与平面垂直的判定
【解析】
由作,垂足为,
由直三棱柱的定义得面,连接,
则为直线与平面所成的角,可得解.
【解答】
解:由作,垂足为,
由直三棱柱的定义得面,连接,如图,
则为直线与平面所成的角,
设,
,
解得.
在,,
,
,
所以,
所以.
故选.
8.
【答案】
C
【考点】
双曲线的定义
双曲线的离心率
【解析】
此题暂无解析
【解答】
解:设双曲线的方程为,
因为该花瓶的瓶口直径为瓶身最小直径的两倍,
所以可得花瓶底面直径为,
因为花瓶恰好能放入与其等高的正方体包装箱,
所以可得该双曲线正好过点,
所以将点代入双曲线方程可得,解得,
所以.
故选.
二、多选题
【答案】
A,D
【考点】
椭圆的定义和性质
双曲线的特性
椭圆的标准方程
圆的标准方程
【解析】
利用双曲线,椭圆,圆的性质对选项一一进行分析解答即可得.
【解答】
解:对:当,则可得,,所以可得曲线表示双曲线,故正确;
对:当,曲线为一个圆,即,
因为,所以无解,
即可得曲线不可能为一个圆,故错误;
对:当时,即时,曲线为椭圆,此时,
所以,
所以椭圆C的长轴为,故错误;
对:当时,可得曲线为椭圆,
所以椭圆的焦点为,
把代入椭圆,即可得,
所以椭圆过焦点最短的弦长为,故正确.
故选.
【答案】
A,B,D
【考点】
点到直线的距离公式
曲线与方程
抛物线的定义
抛物线的应用
【解析】
由抛物线的定义,结合抛物线的相关性质及最值,对四个选项逐一判断即可得到正确答案.
【解答】
解:由题可知,曲线上任意一点到直线的距离与到点的距离相等,
所以曲线的轨迹是以为焦点的抛物线,方程为:,故正确;
由抛物线的定义,到直线的距离为,则点的横坐标为,
代入抛物线方程得纵坐标为,故正确;
设的横坐标为,由抛物线的定义得:,则,
所以线段的中点的横坐标为,故错误;
设点到准线的距离为,由抛物线的定义,,
故正确.
故选.
【答案】
A,C,D
【考点】
直线与平面垂直的性质
直线与平面垂直的判定
球的表面积和体积
【解析】
此题暂无解析
【解答】
解:由题意面,
所以
以为直径的圆过,,
所以面,
面,
可得平面面,故正确.
由,,
,
,故错误.
取的中点,连接,
等边三角形,
,
得为的平面角,
,
故二面角的正切值为,故正确.
由题设三棱锥的外接球直径为,
所以,
.故正确.
故选.
【答案】
B,C,D
【考点】
双曲线的特性
双曲线的标准方程
双曲线的离心率
轨迹方程
圆锥曲线问题的解决方法
点到直线的距离公式
【解析】
此题暂无解析
【解答】
解:由题意得:,,
所以,
所以,
所以,,
,
所以双曲线方程为,
故双曲线的渐近线方程为,故错误;
,故正确;
焦点到双曲线的渐近线距离为,故正确;
设内切圆圆心为,与,,分别相切于,
,,,
所以
,
又,
所以,,圆心横坐标为,
当当交点在坐支上时,同理可得圆心横坐标为,故正确.
故选.
三、填空题
【答案】
【考点】
组合及组合数公式
【解析】
直接组合,排列公式计算即可.
【解答】
解:.
故答案为:.
【答案】
【考点】
双曲线的离心率
双曲线的渐近线
【解析】
结合离心率结合,,之间的关系即可求出结论.
【解答】
解:∵
,
∴
,即,
故双曲线的渐近线方程为.
故答案为:.
【答案】
【考点】
圆与圆的位置关系及其判定
点到直线的距离公式
【解析】
首先求出直线方程,再利用直线与圆相交弦的求法
求解即可.
【解答】
解:把两个圆的方程相减可得直线方程:
,即,
则圆心到直线距离,
故?.
故答案为:.
【答案】
,
【考点】
球的性质
棱柱的结构特征
组合几何体的面积、体积问题
【解析】
由题意作出图形,可得平面截正方体所得截面为等腰梯形
,求出此梯形面积即可,再找出以点M为球心,以为半径的球面与对角面的交线利用弧长公式求解交线长.
【解答】
解:如图,
连接,则,
所以等腰梯形为平面截正方体所得截面图形,
由正方体的棱长为,得,,,
则点到的距离为,
所以,
因为平面平面,且平面平面平面,
过点作于,则平面,
因为点为中点,所以,
以点为球心,以为半径的球面与对角面的交线为圆弧,
其半径为,
由,,得,
所以,
所求交线为劣弧,
长度为,
故答案是.
四、解答题
【答案】
解:因为,,
所以.
,,
所以,
所以与的夹角余弦值为.
,
因为与互相垂直,
所以,解得:,
所以当与互相垂直时,实数的值为.
【考点】
空间向量的数量积运算
用空间向量求直线间的夹角、距离
向量的数量积判断向量的共线与垂直
【解析】
无
无
【解答】
解:因为,,
所以.
,,
所以,
所以与的夹角余弦值为.
,
因为与互相垂直,
所以,解得:,
所以当与互相垂直时,实数的值为.
【答案】
解:圆的方程可化为,
因为,
所以圆心到直线的距离为.
圆心到直线的距离,
所以.
由得直线的方程为.
因为切线与直线平行,
所以设所求的切线方程为.
因为直线与圆相切,
所以圆心到切线的距离.
所以或.
所以所求切线方程为或.
【考点】
圆的标准方程
点到直线的距离公式
直线与圆的位置关系
直线的一般式方程与直线的平行关系
【解析】
无
无
【解答】
解:圆的方程可化为,
因为,
所以圆心到直线的距离为.
圆心到直线的距离,
所以.
由得直线的方程为.
因为切线与直线平行,
所以设所求的切线方程为.
因为直线与圆相切,
所以圆心到切线的距离.
所以或.
所以所求切线方程为或.
【答案】
证明:如图,取的中点为,连接,.
因为,
所以?.?
因为为中点,四边形为菱形,
所以,
所以,
所以四边形为平行四边形,
所以,
因为平面,平面,
以平面.
解:选择条件①:
因为平面,
所以?.?
因为,
所以以为坐标原点,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,,,
所以,,?.?
设平面的一个法向量,
即?
令,则,
设平面的一个法向量,
即
令则,
设平面与平面所成锐二面角为,
则=?.?
所以平面与平面所成锐二面角的余弦值为?.
选条件②:
因为平面,
所以直线与平面所成角为.
因为,
所以,
所以为正三角形.
取中点为,连接,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,
,,,
设平面的一个法向量,
即
令,则,
设平面的一个法向量,
即
令,则,
设平面与平面所成锐二面角为,
则,
所以平面与平面所成锐二面角的余弦值为?
.?
选条件③:
,
所以,
因为,
所以?.?
取中点为,连接,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,
,,,
设平面的一个法向量,
即
令,则,
设平面的一个法向量,
即
令,则,
设平面与平面所成锐二面角为,
则,
所以平面与平面所成锐二面角的余弦值为?
.
【考点】
直线与平面平行的判定
用空间向量求平面间的夹角
【解析】
此题暂无解析
【解答】
证明:如图,取的中点为,连接,.
因为,
所以?.?
因为为中点,四边形为菱形,
所以,
所以,
所以四边形为平行四边形,
所以,
因为平面,平面,
以平面.
解:选择条件①:
因为平面,
所以?.?
因为,
所以以为坐标原点,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,,,
所以,,?.?
设平面的一个法向量,
即?
令,则,
设平面的一个法向量,
即
令则,
设平面与平面所成锐二面角为,
则=
.?
所以平面与平面所成锐二面角的余弦值为?.
选条件②:
因为平面,
所以直线与平面所成角为.
因为,
所以,
所以为正三角形.
取中点为,连接,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,
,,,
设平面的一个法向量,
即
令,则,
设平面的一个法向量,
即
令,则,
设平面与平面所成锐二面角为,
则,
所以平面与平面所成锐二面角的余弦值为?
.?
选条件③:
,
所以,
因为,
所以?.?
取中点为,连接,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图
.?
则,,
,,,
设平面的一个法向量,
即
令,则,
设平面的一个法向量,
即
令,则,
设平面与平面所成锐二面角为,
则,
所以平面与平面所成锐二面角的余弦值为?
.
【答案】
解:以抛物线的顶点为坐标原点,抛物线的对称轴为轴,建立平面直角坐标系,如图
.?
则??,
设抛物线的标准方程为,
因为点在抛物线上,?
所以,
解得,
所以抛物线的方程为?.?
设为灯笼所在点,?为抛物线上设置牵引绳的点,
则,
,
当时,的最小值为,
即一条牵引绳长度的最小值为?.?
【考点】
抛物线的标准方程
二次函数在闭区间上的最值
【解析】
(1)以抛物线的顶点为坐标原点,抛物线的对称轴为轴,建立平面直角坐标系,如图
.?则??,
设抛物线的标准方程为,
因为点在抛物线上,?
所以,解得,
所以抛物线的方程为?.?
【解答】
解:以抛物线的顶点为坐标原点,抛物线的对称轴为轴,建立平面直角坐标系,如图
.?
则??,
设抛物线的标准方程为,
因为点在抛物线上,?
所以,
解得,
所以抛物线的方程为?.?
设为灯笼所在点,?为抛物线上设置牵引绳的点,
则,
,
当时,的最小值为,
即一条牵引绳长度的最小值为?.?
【答案】
证明:因为,,,
所以,
所以.
因为平面,
平面,,
所以.
因为,
所以.
解:存在,由知,且,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图.
,,,
,,.
,,
设
(),
则
.
设平面的一个法向量为,
即
令,则,
设点到平面的距离为,
,
解得或(舍).
所以在线段上存在点,且.
【考点】
两条直线垂直的判定
点、线、面间的距离计算
【解析】
无
无
【解答】
证明:因为,,,
所以,
所以.
因为平面,
平面,,
所以.
因为,
所以.
解:存在,由知,且,以为坐标原点,,,的方向分别为轴,轴,轴的正方向建立空间直角坐标系,如图.
,,,
,,.
,,
设
(),
则
.
设平面的一个法向量为,
即
令,则,
设点到平面的距离为,
,
解得或(舍).
所以在线段上存在点,且.
【答案】
解:由题意设椭圆的标准方程为().
则,
因为
,
所以,
因为在椭圆上,
所以,
解得,
所以,
所以椭圆的标准方程为.
证明:①当直线的斜率不存在时,设:,因为,
所以.
因为以为直径的圆过原点,
所以,得,
.
此时原点到直线的距离为.
②当直线的斜率存在时,设:.
由得,
,
得,
设,,
则,,
.
因为以为直径的圆过原点,
所以,
所以.
此时原点到直线的距离.
综上,原点到直线的距离为定值.
【考点】
椭圆的定义和性质
椭圆的标准方程
直线与椭圆结合的最值问题
椭圆的应用
直线与椭圆的位置关系
【解析】
无
无
【解答】
解:由题意设椭圆的标准方程为().
则,
因为
,
所以,
因为在椭圆上,
所以,
解得,
所以,
所以椭圆的标准方程为.
证明:①当直线的斜率不存在时,设:,因为,
所以.
因为以为直径的圆过原点,
所以,得,
.
此时原点到直线的距离为.
②当直线的斜率存在时,设:.
由得,
,
得,
设,,
则,,
.
因为以为直径的圆过原点,
所以,
所以.
此时原点到直线的距离.
综上,原点到直线的距离为定值.
第7页
共20页
◎
第8页
共20页
第9页
共20页
◎
第10页
共20页
同课章节目录
