2020-2021学年山东省潍坊市高二(上)期中考试数学试卷 (1)人教B版(Word含解析)
文档属性
| 名称 | 2020-2021学年山东省潍坊市高二(上)期中考试数学试卷 (1)人教B版(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 451.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 12:28:18 | ||
图片预览



文档简介
2020-2021学年山东省潍坊市高二(上)期中考试数学试卷
一、选择题
?
1.
若向量与向量共线,则(?
?
?
?
)
A.
B.
C.
D.
?
2.
已知过点,的直线的斜率为,则(?
?
?
?
)
A.
B.
C.
D.
?
3.
圆和圆的位置关系是(?
?
?
?
)
A.外离
B.相交
C.内切
D.外切
?
4.
《九章算术》是我国古代内容极为丰富的数学名著,书中《商功》有如下问题:“今有委粟平地,下周一十二丈,高一丈,问积为粟几何?”,意思是“有粟若干,堆积在平地上,它底圆周长为丈,高为丈,问它的体积和粟各为多少?”如图,主人意欲卖掉该堆粟,已知圆周率约为,一斛粟的体积约为立方寸(单位换算:立方丈立方寸),一斛粟米卖钱,一两银子钱,则主人卖后可得银子(?
?
?
?
)
A.两
B.两
C.两
D.两
?
5.
已知直线与直线垂直,则实数(?
?
?
?
)
A.
B.或
C.或
D.
?
6.
过点,且圆心在直线上的圆的标准方程为(?
?
?
?
)
A.
B.
C.
D.
?
7.
已知棱长为的正方体中,,分别为,的中点,则异面直线与所成的角为(?
?
?
?
)
A.
B.
C.
D.
?
8.
如图,在菱形中,,,是的中点,将沿直线翻折至的位置,使得面面,则点到直线的距离为(?
?
?
?
)
A.
B.
C.
D.
二、多选题
?
若,是两条不同直线,,是两个不同平面,则下列命题正确的是(?
?
?
?
)
A.若,,则
B.若,,则
C.若,,则
D.若,,则
?
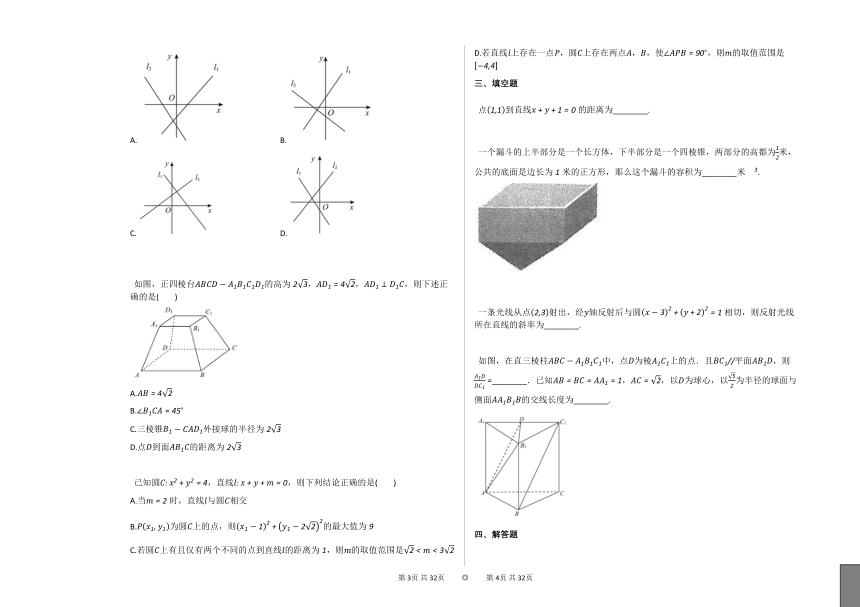
在同一平面直角坐标系中,表示直线:与:的图象可能正确的是(?
?
?
?
)
A.?
B.
C.
D.
?
如图,正四棱台的高为,,,则下述正确的是(?
?
?
?
)
A.
B.
C.三棱锥外接球的半径为
D.点到面的距离为
?
已知圆,直线,则下列结论正确的是(?
?
?
?
)
A.当时,直线与圆相交
B.为圆上的点,则的最大值为
C.若圆上有且仅有两个不同的点到直线的距离为,则的取值范围是
D.若直线上存在一点,圆上存在两点,,使,则的取值范围是
三、填空题
?
点到直线的距离为________.
?
一个漏斗的上半部分是一个长方体,下半部分是一个四棱锥,两部分的高都为米,公共的底面是边长为米的正方形,那么这个漏斗的容积为________米.
?
一条光线从点射出,经轴反射后与圆相切,则反射光线所在直线的斜率为________.
?
如图,在直三棱柱中,点为棱上的点.且平面,则________.已知,,以为球心,以为半径的球面与侧面的交线长度为________.
四、解答题
?
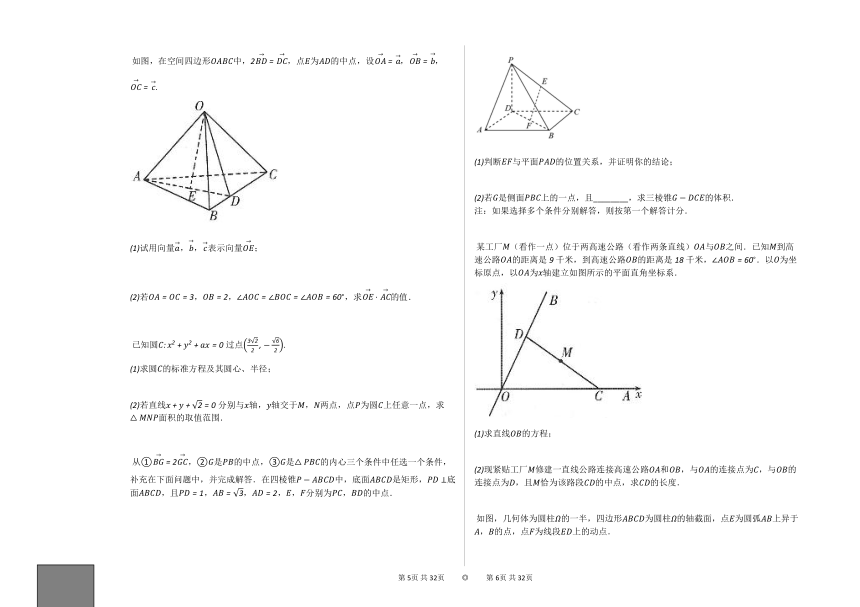
如图,在空间四边形中,,点为的中点,设,,.
试用向量,,表示向量;
若,,,求的值.
?
已知圆过点.
求圆的标准方程及其圆心、半径;
若直线分别与轴,轴交于,两点,点为圆上任意一点,求面积的取值范围.
?
从①,②是的中点,③是的内心三个条件中任选一个条件,补充在下面问题中,并完成解答.在四棱锥中,底面是矩形,底面,且,,,,分别为,的中点.
判断与平面的位置关系,并证明你的结论;
若是侧面上的一点,且________,求三棱锥的体积.
注:如果选择多个条件分别解答,则按第一个解答计分.
?
某工厂(看作一点)位于两高速公路(看作两条直线)与之间.已知到高速公路的距离是千米,到高速公路的距离是千米,.以为坐标原点,以为轴建立如图所示的平面直角坐标系.
求直线的方程;
现紧贴工厂修建一直线公路连接高速公路和,与的连接点为,与的连接点为,且恰为该路段的中点,求的长度.
?
如图,几何体为圆柱的一半,四边形为圆柱的轴截面,点为圆弧上异于,的点,点为线段上的动点.
求证:;
若,,,且直线与平面所成角的正弦值为,求平面与平面所成锐二面角的余弦值.
?
在平面直角坐标系中,点在直线上,,以线段为直径的圆(为圆心)与直线相交于另一个点,.
求圆的标准方程;
若点不在第一象限内,圆与轴的正半轴的交点为,过点作两条直线分别交圆于,两点,且两直线的斜率之积为,试判断直线是否恒过定点,若是,请求出定点的坐标;若不是,请说明理由.
参考答案与试题解析
2020-2021学年山东省潍坊市高二(上)期中考试数学试卷
一、选择题
1.
【答案】
B
【考点】
共线向量与共面向量
【解析】
利用向量共线定理即可得出.
【解答】
解:∵
,共线,
∴
存在实数,使得,
∴
?
解得,,,
∴
.
故选.
2.
【答案】
C
【考点】
斜率的计算公式
【解析】
直接利用斜率公式求解即可.
【解答】
解:由题意可得:,
解得:.
故选.
3.
【答案】
B
【考点】
圆与圆的位置关系及其判定
两点间的距离公式
【解析】
分别由两圆的方程找出两圆心坐标和两个半径和,然后利用两点间的距离公式求出两圆心的距离,比较与及与的大小,即可得到两圆的位置关系.
【解答】
解:圆可转化为.
又,
所以两圆心的坐标分别为:和,两半径分别为和,
所以两圆心之间的距离.
因为,
所以两圆的位置关系是相交.
故选.
4.
【答案】
D
【考点】
柱体、锥体、台体的体积计算
【解析】
首先求出锥体的体积,然后更加相应的价格进行求解即可
【解答】
解:因为有粟若干,堆积在平地上,它底圆周长为丈,高为丈,
所以底面半径?(丈),
所以体积?(立方丈)
?(立方寸),
所以主人卖后可得银子:?(两).
故选.
5.
【答案】
C
【考点】
直线的一般式方程与直线的垂直关系
【解析】
本题先检验时两直线是否垂直,当时,两直线的斜率都存在,由斜率之积等于,解方程求出.
【解答】
解:当实数时,
两直线的方程分别为和,
则两直线垂直.
当时,即两直线的斜率都存在时,
由斜率之积等于,
得,
解得,
综上,或.
故选.
6.
【答案】
A
【考点】
圆的标准方程
点与圆的位置关系
【解析】
本题主要先根据题目意思设出圆心坐标,然后设出圆的标准方程,最后通过两点在圆上联立方程求出圆心坐标与半径,从而求出圆的方程即可
【解答】
解:因为圆心在上,
则设圆心为,
则圆的方程为.
又,在圆上,
则代入圆的方程得:
解得:
所以圆的标准方程为:.
故选.
7.
【答案】
C
【考点】
异面直线及其所成的角
【解析】
本题主要考查异面直线的夹角问题,通过平移到一个图形,结合三角形求出其夹角即可
【解答】
解:因为,分别为,的中点,
所以,
即问题转化为求与所成夹角.
在正方体中,
因为,
所以三角形为等边三角形,
所以两直线夹角为.
故选.
8.
【答案】
A
【考点】
直线与平面垂直的判定
三角形求面积
空间中直线与直线之间的位置关系
【解析】
本题主要根据题目意思找到边长之间的关系,然后根据直接三角形,求出相应边长,最后根据等面积求出点到直线的距离即可
【解答】
解:因为是中点,
所以.
在菱形中,,,
所以是等边三角形,同理是等边三角形,
所以.
又因为点是中点,
所以,,
所以平面平面,
所以平面,
所以.
在直角三角形中,
.
在等腰三角形中,取中点,连,
则,,
所以,
所以,
所以,
所以到的距离为.
故选.
二、多选题
【答案】
A,B,C
【考点】
空间中直线与直线之间的位置关系
空间中直线与平面之间的位置关系
空间中平面与平面之间的位置关系
【解析】
本题中四个选项涉及的命题是在线面关系的背景下研究线线、线面位置关系.两个选项是在线面平行、面面垂直的背景下研究线线平行与线面垂直,两个选项是在线面平行、面面垂直的背景下研究面面垂直与线面垂直分别由线面平行、面面垂直的性质进行判断得出正确选项.
【解答】
解:,由线面垂直的性质定理和线面平行的性质定理可得,若,,则,故正确;
,两条平行线中的一条垂直于一个平面,则另一条直线也垂直于这个平面,故正确;
,若,,由线面平行的性质定理可得,存在直线且,则,则,故正确;
,与的关系,可能平行,也可能垂直,故错误.
故选.
【答案】
A,C
【考点】
函数的图象
【解析】
分别判断两条直线的斜率和截距的符号是否一致即可.
【解答】
解:,的斜率,截距,
的斜率,截距,则,
两个图象一致,满足题意;
,的斜率,截距,
的斜率,截距,则,
两个图象不一致,不满足题意;
,的斜率,截距,
的斜率,截距,则,
两个图象一致,满足题意;
,的斜率,截距,
的斜率,截距,则,
两个图象不一致,不满足题意.
故选.
【答案】
A,B,D
【考点】
柱体、锥体、台体的体积计算
棱台的结构特征
【解析】
此题暂无解析
【解答】
解:,连接,,.
由题意得,,,
∴
.
在中,
,,
∴
,故正确;
,在中,,,
∴
,
∴
.
又,
∴
,故正确;
,∵
,
∴
,故错误;
,∵
,
∴
点到面的距离等于正四棱台的高,即,故正确.
故选.
【答案】
A,D
【考点】
直线与圆的位置关系
直线与圆相交的性质
点到直线的距离公式
【解析】
利用直线与圆的位置关系结论逐项判定,主要是转化为求圆心到直线的距离问题.
【解答】
解:由题意得,圆的圆心为,半径.
,若,则到的距离,
则直线与圆相交,故正确;
,表示到的距离的平方,
其最大值为,故错误;
,由题意可得到的距离满足,
即,即,故错误;
,①当直线与圆有交点时,成立,
即,解得;
②当直线与圆无交点时,或,
过点作圆的两个切线,切点为,,
则,即,
∴
,
∴
,
则,解得,
综上,的取值范围为,故正确.
故选.
三、填空题
【答案】
【考点】
点到直线的距离公式
【解析】
直接代入点到直线距离公式求解即可.
【解答】
解:由点到直线的距离公式可得:
.
故答案为:.
【答案】
【考点】
组合几何体的面积、体积问题
【解析】
漏斗由两个多面体组成,其容积就是两个多面体的体积和.
【解答】
解:由题意知,漏斗的容积即为该几何体的体积,
长方体?的体积,
棱锥的体积,
所以这个漏斗的容积.
故答案为:.
【答案】
或
【考点】
直线的点斜式方程
点到直线的距离公式
直线与圆的位置关系
【解析】
利用对称性设出所求直线,再利用直线与圆相切得关系式,即可得解.
【解答】
解:由光的反射原理知,
反射光线必过点.
设反射光线所在直线的斜率为,
则反射光线所在直线方程为,
即.
又因为光线与圆相切,
所以,
整理得,
解得或.
故答案为:或.
【答案】
,
【考点】
弧长公式
空间中直线与平面之间的位置关系
【解析】
利用线面平行的性质得到线线平行,再作出截面,利用弧长公式即可得到答案.
【解答】
解:如图,连交于点,连结,过点作,
∵
平面,平面,
平面平面,
∴
.
又为的中点,
∴
为的中点,
∴
,
则易得平面,
且.
球面与侧面的交线长,
即以为圆心,为半径的截面圆的劣弧长,如图,
∵
,
∴
,
∴
的长为.
故答案为:;.
四、解答题
【答案】
解:因为,
所以
,
所以
.
因为点为的中点,
所以.
由题意知,,
,,
所以
?.
【考点】
向量加减混合运算及其几何意义
平面向量数量积
【解析】
此题暂无解析
【解答】
解:因为,
所以
,
所以
.
因为点为的中点,
所以.
由题意知,,
,,
所以
?.
【答案】
解:由题意可得,,
解得,
所以圆的方程为,
即圆的标准方程为,
其圆心为,半径为.
由题意可得,,,
所以,
所以圆心到直线的距离为,
所以点到直线的最小距离为,最大距离为,
所以的面积的最小值为,
最大值为,
所以的面积的取值范围为.
【考点】
圆的标准方程与一般方程的转化
点与圆的位置关系
点到直线的距离公式
【解析】
?
?
【解答】
解:由题意可得,,
解得,
所以圆的方程为,
即圆的标准方程为,
其圆心为,半径为.
由题意可得,,,
所以,
所以圆心到直线的距离为,
所以点到直线的最小距离为,最大距离为,
所以的面积的最小值为,
最大值为,
所以的面积的取值范围为.
【答案】
解:平面.
证明如下:
如图,连结,则与交于点,
因为在中,,分别为,的中点,四边形是矩形,
所以.
又因为平面,平面,
所以平面.
因为平面,平面,平面,
所以,.
又因为底面是矩形,
所以.
因为,
所以平面.
在中,为的中点,
所以.
选择条件①.
因为,
所以是的三等分点且.
又因为,
所以三棱锥的高为,
所以?,
所以三棱锥的体积是.
选择条件②.
因为是的中点,是的中点,
所以在中,,
所以三棱锥的高为,
所以,
所以三棱锥的体积是.
选择条件③.
设的内切圆与边相切于点,则,
又因为平面,平面,
所以,
所以,
所以三棱锥的高为.
在中,,,
所以,
所以,
所以
,
所以三棱锥的体积是.
【考点】
直线与平面平行的判定
柱体、锥体、台体的体积计算
直线与平面垂直的判定
直线与平面垂直的性质
【解析】
此题暂无解析
【解答】
证明:连结,则与交于点,
因为在中,,分别为,的中点,
所以.
又因为平面,平面,
所以平面.
因为平面,平面,平面,
所以,.
又因为底面是矩形,
所以.
因为,
所以平面.
在中,为的中点,
所以.
选择条件①.
因为,
所以是的三等分点且.
又因为,
所以三棱锥的高为,
所以?,
所以三棱锥的体积是.
选择条件②.
因为是的中点,是的中点,
所以在中,,
所以三棱锥的高为,
所以,
所以三棱锥的体积是.
选择条件③.
设的内切圆与边相切于点,则,
又因为平面,平面,
所以,
所以,
所以三棱锥的高为.
在中,,,
所以,
所以,
所以
,
所以三棱锥的体积是.
【答案】
解:因为,
所以直线的斜率为,
所以直线的方程为.
设,
因为的方程为,
所以,
解得或(舍)
所以.
设,,
因为为的中点,在上,
所以
解得
所以,
所以公路段的长度为千米.
【考点】
直线的倾斜角
直线的点斜式方程
点到直线的距离公式
中点坐标公式
【解析】
?
?
【解答】
解:因为,
所以直线的斜率为,
所以直线的方程为.
设,
因为的方程为,
所以,
解得或(舍)
所以.
设,,
因为为的中点,在上,
所以
解得
所以,
所以公路段的长度为千米.
【答案】
证明:因为四边形为圆柱的轴截面,
所以为底面半圆的直径,
所以.
因为为圆柱的母线,
所以平面.
因为面,
所以.
因为,面,面,
所以面.
因为面,
所以.
解:在上底面圆弧上取一点,使得为母线,故,,两两垂直.
如图,以点为坐标原点,建立空间直角坐标系.
因为,,
则,,,,,
则.
设,,
则,
则,.
设平面的法向量.
则
得
令,
得,,
所以,.
设与面所成角为,则
,
解得,
所以点为靠近点的三等分点,
则.
取面的法向量.
设平面与平面所成锐二面角为,
,
所以平面与平面所成锐二面角的余弦值为.
【考点】
直线与平面垂直的判定
空间中直线与直线之间的位置关系
用空间向量求平面间的夹角
【解析】
本题首先通过圆的性质有,然后通过线面垂直到线线垂直再到线面垂直,最后得出.
【解答】
证明:因为四边形为圆柱的轴截面,
所以为底面半圆的直径,
所以.
因为为圆柱的母线,
所以平面.
因为面,
所以.
因为,面,面,
所以面.
因为面,
所以.
解:在上底面圆弧上取一点,使得为母线,故,,两两垂直.
如图,以点为坐标原点,建立空间直角坐标系.
因为,,
则,,,,,
则.
设,,
则,
则,.
设平面的法向量.
则
得
令,
得,,
所以,.
设与面所成角为,则
,
解得,
所以点为靠近点的三等分点,
则.
取面的法向量.
设平面与平面所成锐二面角为,
,
所以平面与平面所成锐二面角的余弦值为.
【答案】
解:因为,
所以.
设,
得,
解得,
所以.
在中,,为中点,
所以.
设坐标为,
则,
解得或.
①当时,坐标为,,圆心为,
此时圆的标准方程为;
②当时,坐标为,,圆心为,
此时圆的标准方程为.
综上,圆的标准方程为或.
由题意知,圆的标准方程为,
因为圆与轴的正半轴的交点为,
所以,
所以设直线的方程为,
联立得
消去得,
所以,
所以,
所以,
因为两条直线斜率积为,用代替,得.
①直线的斜率存在,即时,
,
所以直线方程为,
即,
即,则直线过定点;
②当直线的斜率不存在,即时,直线方程为,过定点.
综上可得,直线过定点.
【考点】
圆的标准方程
点到直线的距离公式
圆锥曲线中的定点与定值问题
直线恒过定点
【解析】
根据直线的效率与倾斜角的关系,求出直线的斜率,然后求出点的坐标,最后求得称圆方程;
根据两直线的斜率之积可设出两个方程,然后将来两直线分别与圆联立,求得和的坐标,然后求出直线的方程,要使得过定点,则求出,然后即可求出定点坐标.
【解答】
解:因为,
所以.
设,
得,
解得,
所以.
在中,,为中点,
所以.
设坐标为,
则,
解得或.
①当时,坐标为,,圆心为,
此时圆的标准方程为;
②当时,坐标为,,圆心为,
此时圆的标准方程为.
综上,圆的标准方程为或.
,圆心为,
此时圆的标准方程为.
综上,圆的标准方程为或.
由题意知,圆的标准方程为,
因为圆与轴的正半轴的交点为,
所以,
所以设直线的方程为,
联立得
消去得,
所以,
所以,
所以,
因为两条直线斜率积为,用代替,得.
①直线的斜率存在,即时,
,
所以直线方程为,
即,
即,则直线过定点;
②当直线的斜率不存在,即时,直线方程为,过定点.
综上可得,直线过定点.
第7页
共20页
◎
第8页
共20页
第9页
共20页
◎
第10页
共20页
一、选择题
?
1.
若向量与向量共线,则(?
?
?
?
)
A.
B.
C.
D.
?
2.
已知过点,的直线的斜率为,则(?
?
?
?
)
A.
B.
C.
D.
?
3.
圆和圆的位置关系是(?
?
?
?
)
A.外离
B.相交
C.内切
D.外切
?
4.
《九章算术》是我国古代内容极为丰富的数学名著,书中《商功》有如下问题:“今有委粟平地,下周一十二丈,高一丈,问积为粟几何?”,意思是“有粟若干,堆积在平地上,它底圆周长为丈,高为丈,问它的体积和粟各为多少?”如图,主人意欲卖掉该堆粟,已知圆周率约为,一斛粟的体积约为立方寸(单位换算:立方丈立方寸),一斛粟米卖钱,一两银子钱,则主人卖后可得银子(?
?
?
?
)
A.两
B.两
C.两
D.两
?
5.
已知直线与直线垂直,则实数(?
?
?
?
)
A.
B.或
C.或
D.
?
6.
过点,且圆心在直线上的圆的标准方程为(?
?
?
?
)
A.
B.
C.
D.
?
7.
已知棱长为的正方体中,,分别为,的中点,则异面直线与所成的角为(?
?
?
?
)
A.
B.
C.
D.
?
8.
如图,在菱形中,,,是的中点,将沿直线翻折至的位置,使得面面,则点到直线的距离为(?
?
?
?
)
A.
B.
C.
D.
二、多选题
?
若,是两条不同直线,,是两个不同平面,则下列命题正确的是(?
?
?
?
)
A.若,,则
B.若,,则
C.若,,则
D.若,,则
?
在同一平面直角坐标系中,表示直线:与:的图象可能正确的是(?
?
?
?
)
A.?
B.
C.
D.
?
如图,正四棱台的高为,,,则下述正确的是(?
?
?
?
)
A.
B.
C.三棱锥外接球的半径为
D.点到面的距离为
?
已知圆,直线,则下列结论正确的是(?
?
?
?
)
A.当时,直线与圆相交
B.为圆上的点,则的最大值为
C.若圆上有且仅有两个不同的点到直线的距离为,则的取值范围是
D.若直线上存在一点,圆上存在两点,,使,则的取值范围是
三、填空题
?
点到直线的距离为________.
?
一个漏斗的上半部分是一个长方体,下半部分是一个四棱锥,两部分的高都为米,公共的底面是边长为米的正方形,那么这个漏斗的容积为________米.
?
一条光线从点射出,经轴反射后与圆相切,则反射光线所在直线的斜率为________.
?
如图,在直三棱柱中,点为棱上的点.且平面,则________.已知,,以为球心,以为半径的球面与侧面的交线长度为________.
四、解答题
?
如图,在空间四边形中,,点为的中点,设,,.
试用向量,,表示向量;
若,,,求的值.
?
已知圆过点.
求圆的标准方程及其圆心、半径;
若直线分别与轴,轴交于,两点,点为圆上任意一点,求面积的取值范围.
?
从①,②是的中点,③是的内心三个条件中任选一个条件,补充在下面问题中,并完成解答.在四棱锥中,底面是矩形,底面,且,,,,分别为,的中点.
判断与平面的位置关系,并证明你的结论;
若是侧面上的一点,且________,求三棱锥的体积.
注:如果选择多个条件分别解答,则按第一个解答计分.
?
某工厂(看作一点)位于两高速公路(看作两条直线)与之间.已知到高速公路的距离是千米,到高速公路的距离是千米,.以为坐标原点,以为轴建立如图所示的平面直角坐标系.
求直线的方程;
现紧贴工厂修建一直线公路连接高速公路和,与的连接点为,与的连接点为,且恰为该路段的中点,求的长度.
?
如图,几何体为圆柱的一半,四边形为圆柱的轴截面,点为圆弧上异于,的点,点为线段上的动点.
求证:;
若,,,且直线与平面所成角的正弦值为,求平面与平面所成锐二面角的余弦值.
?
在平面直角坐标系中,点在直线上,,以线段为直径的圆(为圆心)与直线相交于另一个点,.
求圆的标准方程;
若点不在第一象限内,圆与轴的正半轴的交点为,过点作两条直线分别交圆于,两点,且两直线的斜率之积为,试判断直线是否恒过定点,若是,请求出定点的坐标;若不是,请说明理由.
参考答案与试题解析
2020-2021学年山东省潍坊市高二(上)期中考试数学试卷
一、选择题
1.
【答案】
B
【考点】
共线向量与共面向量
【解析】
利用向量共线定理即可得出.
【解答】
解:∵
,共线,
∴
存在实数,使得,
∴
?
解得,,,
∴
.
故选.
2.
【答案】
C
【考点】
斜率的计算公式
【解析】
直接利用斜率公式求解即可.
【解答】
解:由题意可得:,
解得:.
故选.
3.
【答案】
B
【考点】
圆与圆的位置关系及其判定
两点间的距离公式
【解析】
分别由两圆的方程找出两圆心坐标和两个半径和,然后利用两点间的距离公式求出两圆心的距离,比较与及与的大小,即可得到两圆的位置关系.
【解答】
解:圆可转化为.
又,
所以两圆心的坐标分别为:和,两半径分别为和,
所以两圆心之间的距离.
因为,
所以两圆的位置关系是相交.
故选.
4.
【答案】
D
【考点】
柱体、锥体、台体的体积计算
【解析】
首先求出锥体的体积,然后更加相应的价格进行求解即可
【解答】
解:因为有粟若干,堆积在平地上,它底圆周长为丈,高为丈,
所以底面半径?(丈),
所以体积?(立方丈)
?(立方寸),
所以主人卖后可得银子:?(两).
故选.
5.
【答案】
C
【考点】
直线的一般式方程与直线的垂直关系
【解析】
本题先检验时两直线是否垂直,当时,两直线的斜率都存在,由斜率之积等于,解方程求出.
【解答】
解:当实数时,
两直线的方程分别为和,
则两直线垂直.
当时,即两直线的斜率都存在时,
由斜率之积等于,
得,
解得,
综上,或.
故选.
6.
【答案】
A
【考点】
圆的标准方程
点与圆的位置关系
【解析】
本题主要先根据题目意思设出圆心坐标,然后设出圆的标准方程,最后通过两点在圆上联立方程求出圆心坐标与半径,从而求出圆的方程即可
【解答】
解:因为圆心在上,
则设圆心为,
则圆的方程为.
又,在圆上,
则代入圆的方程得:
解得:
所以圆的标准方程为:.
故选.
7.
【答案】
C
【考点】
异面直线及其所成的角
【解析】
本题主要考查异面直线的夹角问题,通过平移到一个图形,结合三角形求出其夹角即可
【解答】
解:因为,分别为,的中点,
所以,
即问题转化为求与所成夹角.
在正方体中,
因为,
所以三角形为等边三角形,
所以两直线夹角为.
故选.
8.
【答案】
A
【考点】
直线与平面垂直的判定
三角形求面积
空间中直线与直线之间的位置关系
【解析】
本题主要根据题目意思找到边长之间的关系,然后根据直接三角形,求出相应边长,最后根据等面积求出点到直线的距离即可
【解答】
解:因为是中点,
所以.
在菱形中,,,
所以是等边三角形,同理是等边三角形,
所以.
又因为点是中点,
所以,,
所以平面平面,
所以平面,
所以.
在直角三角形中,
.
在等腰三角形中,取中点,连,
则,,
所以,
所以,
所以,
所以到的距离为.
故选.
二、多选题
【答案】
A,B,C
【考点】
空间中直线与直线之间的位置关系
空间中直线与平面之间的位置关系
空间中平面与平面之间的位置关系
【解析】
本题中四个选项涉及的命题是在线面关系的背景下研究线线、线面位置关系.两个选项是在线面平行、面面垂直的背景下研究线线平行与线面垂直,两个选项是在线面平行、面面垂直的背景下研究面面垂直与线面垂直分别由线面平行、面面垂直的性质进行判断得出正确选项.
【解答】
解:,由线面垂直的性质定理和线面平行的性质定理可得,若,,则,故正确;
,两条平行线中的一条垂直于一个平面,则另一条直线也垂直于这个平面,故正确;
,若,,由线面平行的性质定理可得,存在直线且,则,则,故正确;
,与的关系,可能平行,也可能垂直,故错误.
故选.
【答案】
A,C
【考点】
函数的图象
【解析】
分别判断两条直线的斜率和截距的符号是否一致即可.
【解答】
解:,的斜率,截距,
的斜率,截距,则,
两个图象一致,满足题意;
,的斜率,截距,
的斜率,截距,则,
两个图象不一致,不满足题意;
,的斜率,截距,
的斜率,截距,则,
两个图象一致,满足题意;
,的斜率,截距,
的斜率,截距,则,
两个图象不一致,不满足题意.
故选.
【答案】
A,B,D
【考点】
柱体、锥体、台体的体积计算
棱台的结构特征
【解析】
此题暂无解析
【解答】
解:,连接,,.
由题意得,,,
∴
.
在中,
,,
∴
,故正确;
,在中,,,
∴
,
∴
.
又,
∴
,故正确;
,∵
,
∴
,故错误;
,∵
,
∴
点到面的距离等于正四棱台的高,即,故正确.
故选.
【答案】
A,D
【考点】
直线与圆的位置关系
直线与圆相交的性质
点到直线的距离公式
【解析】
利用直线与圆的位置关系结论逐项判定,主要是转化为求圆心到直线的距离问题.
【解答】
解:由题意得,圆的圆心为,半径.
,若,则到的距离,
则直线与圆相交,故正确;
,表示到的距离的平方,
其最大值为,故错误;
,由题意可得到的距离满足,
即,即,故错误;
,①当直线与圆有交点时,成立,
即,解得;
②当直线与圆无交点时,或,
过点作圆的两个切线,切点为,,
则,即,
∴
,
∴
,
则,解得,
综上,的取值范围为,故正确.
故选.
三、填空题
【答案】
【考点】
点到直线的距离公式
【解析】
直接代入点到直线距离公式求解即可.
【解答】
解:由点到直线的距离公式可得:
.
故答案为:.
【答案】
【考点】
组合几何体的面积、体积问题
【解析】
漏斗由两个多面体组成,其容积就是两个多面体的体积和.
【解答】
解:由题意知,漏斗的容积即为该几何体的体积,
长方体?的体积,
棱锥的体积,
所以这个漏斗的容积.
故答案为:.
【答案】
或
【考点】
直线的点斜式方程
点到直线的距离公式
直线与圆的位置关系
【解析】
利用对称性设出所求直线,再利用直线与圆相切得关系式,即可得解.
【解答】
解:由光的反射原理知,
反射光线必过点.
设反射光线所在直线的斜率为,
则反射光线所在直线方程为,
即.
又因为光线与圆相切,
所以,
整理得,
解得或.
故答案为:或.
【答案】
,
【考点】
弧长公式
空间中直线与平面之间的位置关系
【解析】
利用线面平行的性质得到线线平行,再作出截面,利用弧长公式即可得到答案.
【解答】
解:如图,连交于点,连结,过点作,
∵
平面,平面,
平面平面,
∴
.
又为的中点,
∴
为的中点,
∴
,
则易得平面,
且.
球面与侧面的交线长,
即以为圆心,为半径的截面圆的劣弧长,如图,
∵
,
∴
,
∴
的长为.
故答案为:;.
四、解答题
【答案】
解:因为,
所以
,
所以
.
因为点为的中点,
所以.
由题意知,,
,,
所以
?.
【考点】
向量加减混合运算及其几何意义
平面向量数量积
【解析】
此题暂无解析
【解答】
解:因为,
所以
,
所以
.
因为点为的中点,
所以.
由题意知,,
,,
所以
?.
【答案】
解:由题意可得,,
解得,
所以圆的方程为,
即圆的标准方程为,
其圆心为,半径为.
由题意可得,,,
所以,
所以圆心到直线的距离为,
所以点到直线的最小距离为,最大距离为,
所以的面积的最小值为,
最大值为,
所以的面积的取值范围为.
【考点】
圆的标准方程与一般方程的转化
点与圆的位置关系
点到直线的距离公式
【解析】
?
?
【解答】
解:由题意可得,,
解得,
所以圆的方程为,
即圆的标准方程为,
其圆心为,半径为.
由题意可得,,,
所以,
所以圆心到直线的距离为,
所以点到直线的最小距离为,最大距离为,
所以的面积的最小值为,
最大值为,
所以的面积的取值范围为.
【答案】
解:平面.
证明如下:
如图,连结,则与交于点,
因为在中,,分别为,的中点,四边形是矩形,
所以.
又因为平面,平面,
所以平面.
因为平面,平面,平面,
所以,.
又因为底面是矩形,
所以.
因为,
所以平面.
在中,为的中点,
所以.
选择条件①.
因为,
所以是的三等分点且.
又因为,
所以三棱锥的高为,
所以?,
所以三棱锥的体积是.
选择条件②.
因为是的中点,是的中点,
所以在中,,
所以三棱锥的高为,
所以,
所以三棱锥的体积是.
选择条件③.
设的内切圆与边相切于点,则,
又因为平面,平面,
所以,
所以,
所以三棱锥的高为.
在中,,,
所以,
所以,
所以
,
所以三棱锥的体积是.
【考点】
直线与平面平行的判定
柱体、锥体、台体的体积计算
直线与平面垂直的判定
直线与平面垂直的性质
【解析】
此题暂无解析
【解答】
证明:连结,则与交于点,
因为在中,,分别为,的中点,
所以.
又因为平面,平面,
所以平面.
因为平面,平面,平面,
所以,.
又因为底面是矩形,
所以.
因为,
所以平面.
在中,为的中点,
所以.
选择条件①.
因为,
所以是的三等分点且.
又因为,
所以三棱锥的高为,
所以?,
所以三棱锥的体积是.
选择条件②.
因为是的中点,是的中点,
所以在中,,
所以三棱锥的高为,
所以,
所以三棱锥的体积是.
选择条件③.
设的内切圆与边相切于点,则,
又因为平面,平面,
所以,
所以,
所以三棱锥的高为.
在中,,,
所以,
所以,
所以
,
所以三棱锥的体积是.
【答案】
解:因为,
所以直线的斜率为,
所以直线的方程为.
设,
因为的方程为,
所以,
解得或(舍)
所以.
设,,
因为为的中点,在上,
所以
解得
所以,
所以公路段的长度为千米.
【考点】
直线的倾斜角
直线的点斜式方程
点到直线的距离公式
中点坐标公式
【解析】
?
?
【解答】
解:因为,
所以直线的斜率为,
所以直线的方程为.
设,
因为的方程为,
所以,
解得或(舍)
所以.
设,,
因为为的中点,在上,
所以
解得
所以,
所以公路段的长度为千米.
【答案】
证明:因为四边形为圆柱的轴截面,
所以为底面半圆的直径,
所以.
因为为圆柱的母线,
所以平面.
因为面,
所以.
因为,面,面,
所以面.
因为面,
所以.
解:在上底面圆弧上取一点,使得为母线,故,,两两垂直.
如图,以点为坐标原点,建立空间直角坐标系.
因为,,
则,,,,,
则.
设,,
则,
则,.
设平面的法向量.
则
得
令,
得,,
所以,.
设与面所成角为,则
,
解得,
所以点为靠近点的三等分点,
则.
取面的法向量.
设平面与平面所成锐二面角为,
,
所以平面与平面所成锐二面角的余弦值为.
【考点】
直线与平面垂直的判定
空间中直线与直线之间的位置关系
用空间向量求平面间的夹角
【解析】
本题首先通过圆的性质有,然后通过线面垂直到线线垂直再到线面垂直,最后得出.
【解答】
证明:因为四边形为圆柱的轴截面,
所以为底面半圆的直径,
所以.
因为为圆柱的母线,
所以平面.
因为面,
所以.
因为,面,面,
所以面.
因为面,
所以.
解:在上底面圆弧上取一点,使得为母线,故,,两两垂直.
如图,以点为坐标原点,建立空间直角坐标系.
因为,,
则,,,,,
则.
设,,
则,
则,.
设平面的法向量.
则
得
令,
得,,
所以,.
设与面所成角为,则
,
解得,
所以点为靠近点的三等分点,
则.
取面的法向量.
设平面与平面所成锐二面角为,
,
所以平面与平面所成锐二面角的余弦值为.
【答案】
解:因为,
所以.
设,
得,
解得,
所以.
在中,,为中点,
所以.
设坐标为,
则,
解得或.
①当时,坐标为,,圆心为,
此时圆的标准方程为;
②当时,坐标为,,圆心为,
此时圆的标准方程为.
综上,圆的标准方程为或.
由题意知,圆的标准方程为,
因为圆与轴的正半轴的交点为,
所以,
所以设直线的方程为,
联立得
消去得,
所以,
所以,
所以,
因为两条直线斜率积为,用代替,得.
①直线的斜率存在,即时,
,
所以直线方程为,
即,
即,则直线过定点;
②当直线的斜率不存在,即时,直线方程为,过定点.
综上可得,直线过定点.
【考点】
圆的标准方程
点到直线的距离公式
圆锥曲线中的定点与定值问题
直线恒过定点
【解析】
根据直线的效率与倾斜角的关系,求出直线的斜率,然后求出点的坐标,最后求得称圆方程;
根据两直线的斜率之积可设出两个方程,然后将来两直线分别与圆联立,求得和的坐标,然后求出直线的方程,要使得过定点,则求出,然后即可求出定点坐标.
【解答】
解:因为,
所以.
设,
得,
解得,
所以.
在中,,为中点,
所以.
设坐标为,
则,
解得或.
①当时,坐标为,,圆心为,
此时圆的标准方程为;
②当时,坐标为,,圆心为,
此时圆的标准方程为.
综上,圆的标准方程为或.
,圆心为,
此时圆的标准方程为.
综上,圆的标准方程为或.
由题意知,圆的标准方程为,
因为圆与轴的正半轴的交点为,
所以,
所以设直线的方程为,
联立得
消去得,
所以,
所以,
所以,
因为两条直线斜率积为,用代替,得.
①直线的斜率存在,即时,
,
所以直线方程为,
即,
即,则直线过定点;
②当直线的斜率不存在,即时,直线方程为,过定点.
综上可得,直线过定点.
第7页
共20页
◎
第8页
共20页
第9页
共20页
◎
第10页
共20页
同课章节目录
