2021-2022学年人教版数学八年级上册14.2.1 平方差公式 教学课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册14.2.1 平方差公式 教学课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 08:08:07 | ||
图片预览






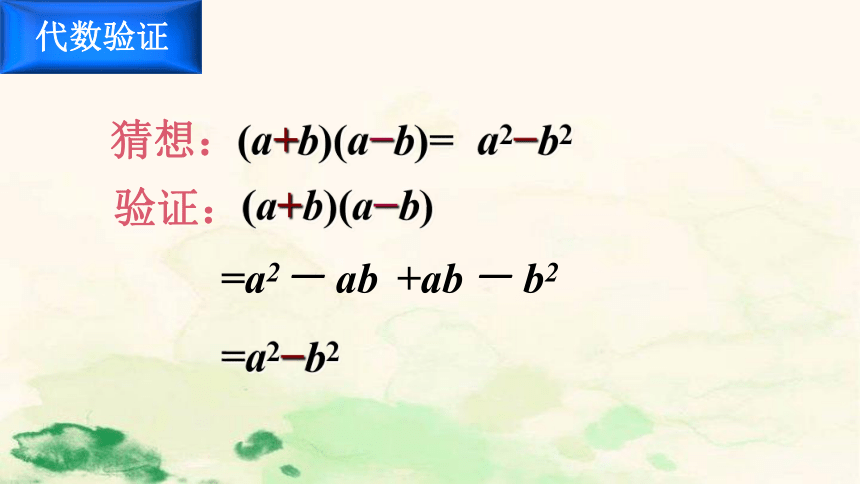

文档简介
(共21张PPT)
一个狡猾的地主把一块边长为a米的正方形土地租给阿凡提。有一天,地主提出要把这块地的一边增加5米,另一边减少5米,以同样租金租给阿凡提,聪明的阿凡提听后,想了想说:我要是这样租了你的土地,我不就吃亏了吗?
同学们,你认为阿凡提吃亏了吗?为什么?
创设情境
14.2.1平方差公式
§14.2
乘法公式
第十四章
整式的乘法和因式分解
八年级上册
温馨提示:课件中所有视频、动画、声音请在幻灯片下观看,如不能观看,请更换设备或电脑观看。
1.知识与技能:掌握平方差公式的结构特征,并能运用公式进行简单的计算.
2.过程与方法:在探索平方差公式的过程中,体会数形结合的思想方法,进一步发展学生的符号感和观察、推理、归纳能力.
3.情感态度:在计算的过程中发现规律,并能用符号语言表达,从而体会数学语言的简洁美.
学习目标
多项式与多项式相乘
(a+b)(p+q)
=ap
+
aq
+
bp
+
bq
计算下列各题
①(x
+
4)(
x-4)
②(1
+
2a)(
1-2a)
③(m+
6n)(
m-6n)
④(5y
+
z)(5y-z)
温故知新
②(1
+
2a)(
1-2a)=1
-4a2
③(m+
6n)(
m-6n)=m2
-
36n2
④(5y
+
z)(5y-z)=
25y2
-
z2
①(x
+
4)(
x-4)=x2
-
16
你能发现什么规律?
x2
-
42
12-(2a)2
m2
-
(6n)2
(5y)2
-
z2
(a+b)(a?b)=
a2?b2
探索新知
猜想:
(a+b)(a?b)=
a2?b2
=a2
验证:
(a+b)(a?b)
代数验证
猜想:
=a2?b2
-
ab
+ab
-
b2
1、平方差公式:
a2?b2
(a+b)(a?b)=
2、语言叙述:
两个数的和与这两个数差的积,等于这两个数的平方差.
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
=
a-b
a-b
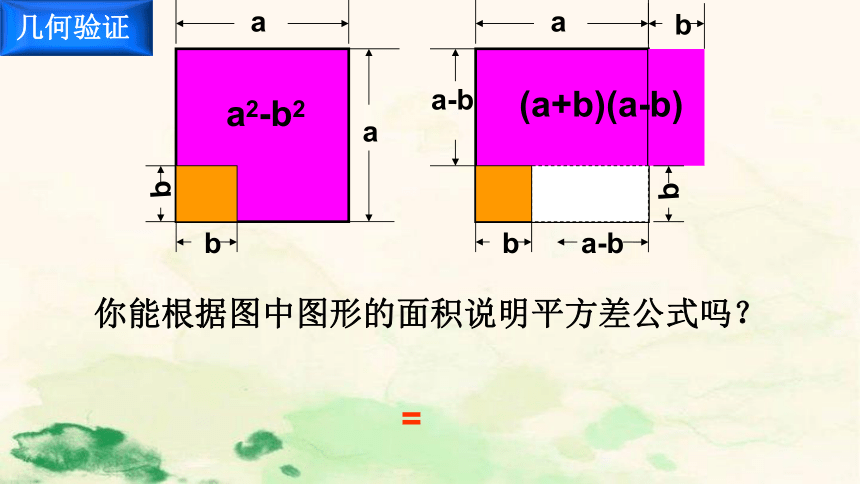
几何验证
你能根据图中图形的面积说明平方差公式吗?
(1)
(3x+2
)(
3x-2
)
;(2)
(-x+2y)(-x-2y).
(3)
(y+2)
(y-2)
–
(y-1)
(y+5)
解:
(1)
(3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(2)
(-x+2y)(-x-2y)
=(-x)2-(2y)2
=
x2-4y2
注意
?
注意结构特征
学会对号入座
例题讲解1
(3)(y+2)(y-2)-
(y-1)(y+5)
=
y2-22-(y2+4y-5)
=
y2-4-y2-4y+5
=
-
4y
+
1.
(a+b)(a-b)=a2-b2
相反项
(相同项)2-(相反项)2
相同项
注:公式中的字母a、b可以表示数,也可以是表示数的单项式、多项式.
公式特征
口答下列各题:
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)=
__________
(3)(-a-b)(-a+b)=
________
(4)(a-b)(-a-b)=
_________
a2-b2
a2-b2
b2-a2
b2-a2
公式变形:
口答下列各题:
(l)(a+3b)(a-3b)=??_____
(2)(-3m+2n)(-3m-2n)=
_____
(3)(-3a-2)(3a-2)=
(4)(1+4x)(4x-1)=
9m2-4n2
a2-9b2
快速抢答
4-9a2
下列式子能用平方差公式运算吗?若能,它们是哪两个数的平方差?
能,(a-c)与b的平方差.
思考延伸
2.
(a+b-c)(a-b-c)
1.
(-3a-2)(3a-2)
能,-2与3a的平方差
(-3a-2)(3a-2)=
-(3a+2)(3a-2)
或3a与2的平方差
(1)
102×98
(2)
(a-2)(a+2)(a2
+
4)
解:
(1)
102×98
=
1002-22
=
1000
–
4
=(100+2)(100-2)
=
9996
例题讲解2
解:
(2)
(a-2)(a+2)(a2
+
4)
=(a2-
4)(a2
+
4)
=(a2
)
-
42
=a4
-16
2
计算:(2+1)(22+1)(24+1)(28+1)
乘以(2-1)得:
解:原式
=
(2-1)(2+1)(22+1)(24+1)(28+1)
=
(22-1)(22+1)(24+1)(28+1)
=
(24-1)(24+1)(28+1)
=(28-1)(28+1)
=
216-1
挑战极限
5米
5米
a米
(a-5)
(a+5)米
原来
改后
通过本节课的学习,你认为阿凡提亏了吗?为什么?
a2
(a+5)(a-5)
改后面积:(a+5)(a-5)=a?-25
原来面积:a?
解决问题
1、平方差公式
(a+b)(a?b)=a2?b2
2、公式的结构特征
3、运用平方差公式的步骤
先比形式,再套公式
课堂小结
(相同项)2-(相反项)2
1.必做题:课本108页第2题;112页,第5题.
2.选做题:综合拓展.
①
20042
-
2003×2005;
②(x-y)(x+y
)(x2+y2
)(x4+y4
)
分层作业
本节课结束
同学们,再见!
1.必做题:课本108页第2题;112页,第5题.
2.选做题:综合拓展.
①
20042
-
2003×2005;
②(x-y)(x+y
)(x2+y2
)(x4+y4
)
分层作业
一个狡猾的地主把一块边长为a米的正方形土地租给阿凡提。有一天,地主提出要把这块地的一边增加5米,另一边减少5米,以同样租金租给阿凡提,聪明的阿凡提听后,想了想说:我要是这样租了你的土地,我不就吃亏了吗?
同学们,你认为阿凡提吃亏了吗?为什么?
创设情境
14.2.1平方差公式
§14.2
乘法公式
第十四章
整式的乘法和因式分解
八年级上册
温馨提示:课件中所有视频、动画、声音请在幻灯片下观看,如不能观看,请更换设备或电脑观看。
1.知识与技能:掌握平方差公式的结构特征,并能运用公式进行简单的计算.
2.过程与方法:在探索平方差公式的过程中,体会数形结合的思想方法,进一步发展学生的符号感和观察、推理、归纳能力.
3.情感态度:在计算的过程中发现规律,并能用符号语言表达,从而体会数学语言的简洁美.
学习目标
多项式与多项式相乘
(a+b)(p+q)
=ap
+
aq
+
bp
+
bq
计算下列各题
①(x
+
4)(
x-4)
②(1
+
2a)(
1-2a)
③(m+
6n)(
m-6n)
④(5y
+
z)(5y-z)
温故知新
②(1
+
2a)(
1-2a)=1
-4a2
③(m+
6n)(
m-6n)=m2
-
36n2
④(5y
+
z)(5y-z)=
25y2
-
z2
①(x
+
4)(
x-4)=x2
-
16
你能发现什么规律?
x2
-
42
12-(2a)2
m2
-
(6n)2
(5y)2
-
z2
(a+b)(a?b)=
a2?b2
探索新知
猜想:
(a+b)(a?b)=
a2?b2
=a2
验证:
(a+b)(a?b)
代数验证
猜想:
=a2?b2
-
ab
+ab
-
b2
1、平方差公式:
a2?b2
(a+b)(a?b)=
2、语言叙述:
两个数的和与这两个数差的积,等于这两个数的平方差.
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
=
a-b
a-b
几何验证
你能根据图中图形的面积说明平方差公式吗?
(1)
(3x+2
)(
3x-2
)
;(2)
(-x+2y)(-x-2y).
(3)
(y+2)
(y-2)
–
(y-1)
(y+5)
解:
(1)
(3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(2)
(-x+2y)(-x-2y)
=(-x)2-(2y)2
=
x2-4y2
注意
?
注意结构特征
学会对号入座
例题讲解1
(3)(y+2)(y-2)-
(y-1)(y+5)
=
y2-22-(y2+4y-5)
=
y2-4-y2-4y+5
=
-
4y
+
1.
(a+b)(a-b)=a2-b2
相反项
(相同项)2-(相反项)2
相同项
注:公式中的字母a、b可以表示数,也可以是表示数的单项式、多项式.
公式特征
口答下列各题:
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)=
__________
(3)(-a-b)(-a+b)=
________
(4)(a-b)(-a-b)=
_________
a2-b2
a2-b2
b2-a2
b2-a2
公式变形:
口答下列各题:
(l)(a+3b)(a-3b)=??_____
(2)(-3m+2n)(-3m-2n)=
_____
(3)(-3a-2)(3a-2)=
(4)(1+4x)(4x-1)=
9m2-4n2
a2-9b2
快速抢答
4-9a2
下列式子能用平方差公式运算吗?若能,它们是哪两个数的平方差?
能,(a-c)与b的平方差.
思考延伸
2.
(a+b-c)(a-b-c)
1.
(-3a-2)(3a-2)
能,-2与3a的平方差
(-3a-2)(3a-2)=
-(3a+2)(3a-2)
或3a与2的平方差
(1)
102×98
(2)
(a-2)(a+2)(a2
+
4)
解:
(1)
102×98
=
1002-22
=
1000
–
4
=(100+2)(100-2)
=
9996
例题讲解2
解:
(2)
(a-2)(a+2)(a2
+
4)
=(a2-
4)(a2
+
4)
=(a2
)
-
42
=a4
-16
2
计算:(2+1)(22+1)(24+1)(28+1)
乘以(2-1)得:
解:原式
=
(2-1)(2+1)(22+1)(24+1)(28+1)
=
(22-1)(22+1)(24+1)(28+1)
=
(24-1)(24+1)(28+1)
=(28-1)(28+1)
=
216-1
挑战极限
5米
5米
a米
(a-5)
(a+5)米
原来
改后
通过本节课的学习,你认为阿凡提亏了吗?为什么?
a2
(a+5)(a-5)
改后面积:(a+5)(a-5)=a?-25
原来面积:a?
解决问题
1、平方差公式
(a+b)(a?b)=a2?b2
2、公式的结构特征
3、运用平方差公式的步骤
先比形式,再套公式
课堂小结
(相同项)2-(相反项)2
1.必做题:课本108页第2题;112页,第5题.
2.选做题:综合拓展.
①
20042
-
2003×2005;
②(x-y)(x+y
)(x2+y2
)(x4+y4
)
分层作业
本节课结束
同学们,再见!
1.必做题:课本108页第2题;112页,第5题.
2.选做题:综合拓展.
①
20042
-
2003×2005;
②(x-y)(x+y
)(x2+y2
)(x4+y4
)
分层作业
