3.1.2 函数的表示法 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共16张PPT)
文档属性
| 名称 | 3.1.2 函数的表示法 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 20:57:35 | ||
图片预览






文档简介
(共16张PPT)
数学(人教A版2019)
必修第一册
第三章
函数的概念与性质
3.1.2 函数的表示法
复习回顾
问题1:某“复兴号”高速列车到350km/h后保持匀速运行半小时。这段时间内,列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示为S=350t,
问题2:
某电气维修告诉要求工人每周工作至少1天,至多不超过6天。如果
公司确定的工资标准是每人每天350元,而且每周付一次工资.工资w
(单位:元)是他工作天数d的函数,
对应关系为w=350d,其中,
用数学表达式表示两个变量之间的对应关系。
——解析法
问题3:
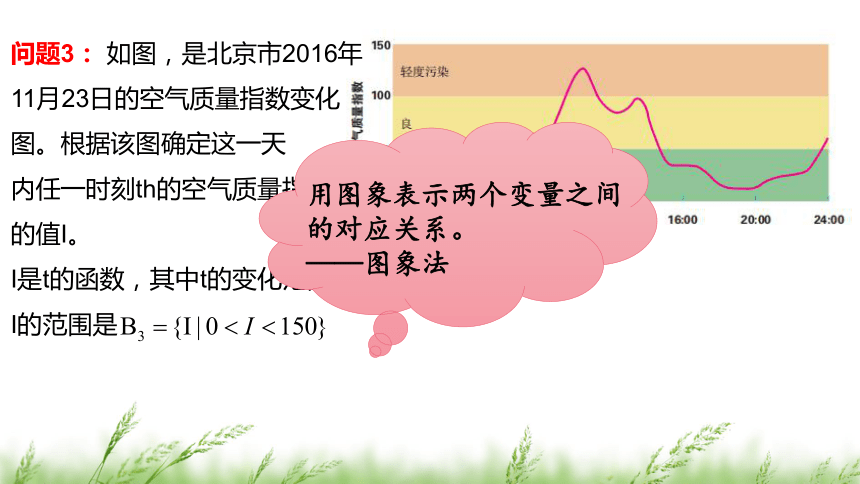
如图,是北京市2016年
11月23日的空气质量指数变化
图。根据该图确定这一天
内任一时刻th的空气质量指数
的值I。
I是t的函数,其中t的变化范围是
I的范围是
用图象表示两个变量之间的对应关系。
——图象法
问题4:国际上常用恩格尔系数
反映一个地区人民生
活质量的高低,恩格尔系数越低,生活质量越高。上表是我国某省城镇
居民恩格尔系数变化情况,从表中可以看出,该省城镇居民的生活质量越来
越高。该表给出的对应关系,恩格尔系数r是年份y的函数
y的取值范围是
列出表格不表示两个变量之间的对应关系。
——列表法
函数的表示法
优点
缺点
解析法
函数关系清楚,容易从自变量的值求出其对应的函数值,便于用解析式来研究函数的性质
一些实际问题很难找到它的解析式
图象法
能直观形象地表示出函数的变化情况
只能近似地求出自变量的值所对应的函数值,有时误差较大
列表法
不必通过计算就知道当自变量取某些值时函数的对应值
一般用于自变量为有限个的函数
重难点突破
函数解析式的多种求法
方法1:待定系数法求函数解析式
变式训练
方法2:换元法(或配凑法)求函数解析式
例2.
变式训练
已知f(x+1)=x2-3x+2,
方法3:构造方程组法求函数解析式
例3.
变式训练
1.待定系数法:已知函数类型时,常用待定系数法。
2.换元法:已知
的解析式,求
的解析式,可用换元法,即令
,反解出
,然后带入
中求出
,从而求出
。
3.配凑法:通过公式变形能进行整体代换。
4.构造方程组法:当同一个对应关系中的两个自变量之间的互为相反数后者互为倒数关系时,构造方程求解。
规律总结
1.本节主要学习了哪些内容?
2.各种方法分别都适用于什么样的式
子去求解析式?
课堂小结
作业
1.已知
是二次函数,且
求
的解析式.
2.已知f(x)=2f(-x)+x2+2x,求f(x)的解析式.
谢谢指导!
数学(人教A版2019)
必修第一册
第三章
函数的概念与性质
3.1.2 函数的表示法
复习回顾
问题1:某“复兴号”高速列车到350km/h后保持匀速运行半小时。这段时间内,列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示为S=350t,
问题2:
某电气维修告诉要求工人每周工作至少1天,至多不超过6天。如果
公司确定的工资标准是每人每天350元,而且每周付一次工资.工资w
(单位:元)是他工作天数d的函数,
对应关系为w=350d,其中,
用数学表达式表示两个变量之间的对应关系。
——解析法
问题3:
如图,是北京市2016年
11月23日的空气质量指数变化
图。根据该图确定这一天
内任一时刻th的空气质量指数
的值I。
I是t的函数,其中t的变化范围是
I的范围是
用图象表示两个变量之间的对应关系。
——图象法
问题4:国际上常用恩格尔系数
反映一个地区人民生
活质量的高低,恩格尔系数越低,生活质量越高。上表是我国某省城镇
居民恩格尔系数变化情况,从表中可以看出,该省城镇居民的生活质量越来
越高。该表给出的对应关系,恩格尔系数r是年份y的函数
y的取值范围是
列出表格不表示两个变量之间的对应关系。
——列表法
函数的表示法
优点
缺点
解析法
函数关系清楚,容易从自变量的值求出其对应的函数值,便于用解析式来研究函数的性质
一些实际问题很难找到它的解析式
图象法
能直观形象地表示出函数的变化情况
只能近似地求出自变量的值所对应的函数值,有时误差较大
列表法
不必通过计算就知道当自变量取某些值时函数的对应值
一般用于自变量为有限个的函数
重难点突破
函数解析式的多种求法
方法1:待定系数法求函数解析式
变式训练
方法2:换元法(或配凑法)求函数解析式
例2.
变式训练
已知f(x+1)=x2-3x+2,
方法3:构造方程组法求函数解析式
例3.
变式训练
1.待定系数法:已知函数类型时,常用待定系数法。
2.换元法:已知
的解析式,求
的解析式,可用换元法,即令
,反解出
,然后带入
中求出
,从而求出
。
3.配凑法:通过公式变形能进行整体代换。
4.构造方程组法:当同一个对应关系中的两个自变量之间的互为相反数后者互为倒数关系时,构造方程求解。
规律总结
1.本节主要学习了哪些内容?
2.各种方法分别都适用于什么样的式
子去求解析式?
课堂小结
作业
1.已知
是二次函数,且
求
的解析式.
2.已知f(x)=2f(-x)+x2+2x,求f(x)的解析式.
谢谢指导!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
